Исследование закрученной струи газа, истекающей из вихревого струйного захватного устройства на плоскую преграду

Вихревые струйные захватные устройства (ВСЗУ), принцип действия которых основан на использовании энергии закрученной струи газа или жидкости, широко применяются в различных отраслях промышленности [1, 2]. В первую очередь, это области топочной техники и энерготехнологии.

Эффект температурного разделения газа (эффект Ранка), открытый в 1931 году, широко используется в технике, например в вихревых холодильниках, а также в системах осушки и регенерации газов и жидкости. Эжектирующее свойство вихревого потока широко применяют для образования рабочих смесей в вихревых смесителях, для транспортирования различных масс с одной позиции на другую, для вакуумирования рабочих объемов и для разделения смесей на составляющие их компоненты. Тело, помещенное во вращающийся вихревой поток, приобретает сложное колебательное движение, состоящее из вращения, обкатки со скольжением, осевого перемещения и прецессионного движения тела вокруг оси вихревой трубы. Таким образом, тело, находящееся в вихревой трубе, совершает поисковое (ориентирующее) движение относительно другого неподвижного тела. Кроме этого, перспективным следует считать применение вихревых камер для упрочнения и очистки поверхности деталей, нанесения лакокрасочных и других покрытий.

В классических вихревых устройствах воздух выходит через центральное отверстие диаметром, меньшим диаметра вихревой камеры, при этом, как известно [3, 4], тангенциальная составляющая скорости в центральной части изменяется по закону вращения твердого тела ( v _ф /г = const). На определенном радиусе r max тангенциальная скорость достигает своего максимального значения, а затем уменьшается по закону квазипотенциального течения ( v _ф r n = const), где п может принимать значения, отличные от единицы.

На радиусе, где v _ф = v _ф max , избыточное давление равно нулю. В зависимости от размера выходного центрального отверстия меняется величина и положение максимальной окружной скорости.

Известно множество работ по экспериментальному и теоретическому определению v _фтах и радиуса r max , [3-6]. Вихревые устройства обычно имеют оптимальный диаметр выходного отверстия, при котором v _{φ max} и разрежение на оси будут наибольшими. При уменьшении этого диаметра уменьшаются v φ max и разрежение, которое затем совсем исчезает, а при увеличении диаметра отверстия также происходит уменьшение данных величин, однако область разрежения увеличивается. При этом v φ max , уменьшаясь, сдвигается к периферии.

Недостатком вышеназванных работ является то, что в них не рассматриваются случаи, когда закрученная воздушная струя выходит не через центральное отверстие, а через боковой кольцевой зазор малых размеров, что имеет место, когда воздушный поток на своем пути встречает преграду, которая может располагаться на разном расстоянии от устройства. В этом случае воздушные струи перемещаются не к центру устройства, а от него; это становится возможным, если отверстие расширяется при выходе из камеры. Воздух при этом истекает через – 172 – боковую кольцевую щель высотой h, как и в предлагаемой нами новой конструкции ВСЗУ [7-9].

Объекты и методики исследований

Предлагаемое устройство ВСЗУ (рис. 1) состоит из цилиндрической камеры 1 диаметром d k , плавно переходящей в развитой торец (насадок) 2 , имеющий диаметр D . В верхней части имеется кожух 3 , создающий замкнутую полость вокруг камеры для подачи воздуха в четыре отверстия 4 диаметром d c .

Сжатый воздух постоянного давления p_u подается через отверстие 5 в замкнутую полость вокруг камеры 3 , далее, проходя через тангенциальные отверстия 4 в стенках камеры и попадая в цилиндрическую камеру, он закручивается.

В верхней части камеры имеется отверстие, которое либо закрывается пробкой 6 , либо там устанавливается специальная вставка, позволяющая сузить зазор на выходе из камеры и увеличить присасывающий эффект устройства. Последний вариант в данной работе не рассматривается.

При спиральном движении воздуха в цилиндрической камере 1 его скорость имеет три составляющие: радиальную v r. , тангенциальную v _ф и осевую v _z . При этом радиальная составляющая скорости v r значительно меньше тангенциальной v φ и осевой v z компонент до тех пор, пока цилиндрическая камера не будет переходить плавно в торцовую поверхность.

В нижней части устройства радиальная составляющая v r становится соизмеримой с тангенциальной v _φ, а осевая составляющая v_z , наоборот, становится незначительной в том случае,

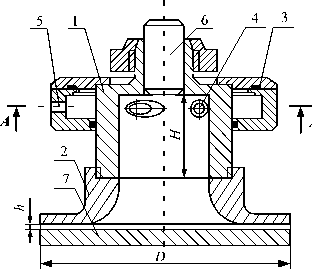
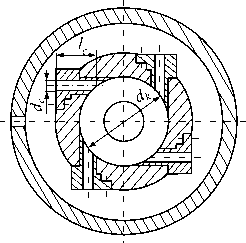
Рис. 1. Вихревое струйное захватное устройство

Fig. 1. Vortex jet gripping device если на пути истекающего из камеры воздуха устанавливается преграда, каковой и является пластина 7.

При приближении захватного устройства к поверхности пластины 7 зазор h между торцом и пластиной уменьшается, в результате чего значительно возрастает радиальная составляющая скорости v_r , которая будет иметь наибольшее значение на выходе из камеры в радиальную щель. Тангенциальная составляющая скорости v φ уменьшается при удалении от оси камеры.

Эффект увеличения радиальной скорости приводит к снижению статического давления ниже атмосферного, причем наибольшее разрежение возникает при определенной величине зазора h , дальнейшее уменьшение которого вызовет увеличение силы струи, которая будет стремиться оттолкнуть пластину 7

Если на торце ВСЗУ нет никаких упоров, ограничивающих движение пластины 7 по оси, то она начинает колебаться около определенного положения, то приближаясь, то отдаляясь от торца, при этом не будет достигнуто наилучших условий работы.

В основу существующих конструкций ВСЗУ положен известный эффект присасывающего действия струи, истекающей из отверстия малого диаметра и взаимодействующей с обтекаемой ею плоской, цилиндрической или сферической поверхностью, и вихревой эффект, который заключается в следующем. Под действием центробежных сил, возникающих во вращающемся потоке, частицы газа смещаются в периферийную область камеры, образуя спиральную вихревую струю. В приосевой области образуются зоны разрежения (зоны обратных потоков).

Характерной особенностью взаимодействия закрученной струи с плоской преградой является то, что при расположении преграды в непосредственной близости от торцовой поверхности вихревой камеры возникает отрицательное избыточное давление.

В этом случае истекающая из цилиндрической камеры струя прилипает к торцовой поверхности и притягивает преграду. Согласно распределению статического давления на преграде суммарная отрицательная сила (притягивающая), действующая на преграду, превышает суммарную положительную силу (отталкивающую). Этот эффект позволяет использовать вихревую камеру в качестве бесконтактного или с контактом (в зависимости от функциональных требований) газостатического подвеса.

Выход воздуха через периферийную щель способствует увеличению разрежения за счет повышения радиальной скорости, которая вызывает эжекцию в центральной части, и градиент радиальной скорости вызывает понижение давления, т.к. если пренебречь осевой составляющей скорости, то

∂ p   ^v ϕ      ∂ v    ∂ ² v

= ρ - ρvr   r + µ r .

∂ r    r      ∂ r    ∂ z ²

Из этой зависимости видно, что давление уменьшается сильнее, если градиент радиальной скорости будет положительным, т.е. радиальная скорость будет увеличиваться при удалении от центра. Это возможно в том случае, если v r на входе в кольцевой зазор будет равна скорости звука, тогда дальнейшее увеличение площади кольцевой щели вызовет увеличение скорости и падение давления, как в сопле Лаваля [10].

При дозвуковом течении положительный градиент радиальной скорости можно получить уменьшением площади кольцевого зазора.

Таким образом, подъемная (притягивающая) сила F, удерживающая пластину 7, будет возникать за счет:

• -    разрежения в центре вихря;

• -    разрежения в результате эжекции из приосевой области при высокоскоростном истечении воздуха через щель в атмосферу;

• -    разрежения в области торца из-за значительного повышения составляющей скорости v r ;

• -    сил вязкостного трения.

Течение газа, как было сказано выше, существенно трехмерно, но все параметры течения периодически (через каждые 90°) повторяются, если двигаться по окружности. В связи с этим предложено брать расчетную сетку в виде 1/4 реального устройства (рис. 2).

Течение газа в полости устройства считаем установившимся. Используем ортогональную систему координат. Ось z направим вдоль геометрической оси устройства, а оси x и у будем располагать в плоскости пластины. Искомыми функциями служат три компонента вектора скорости u, v , w , являющихся проекциями вектора скорости на оси координат x , y, z соответственно, и давление р.

Для учета турбулентности будем использовать так называемую к- е - модель турбулентности [11]. В соответствии с этой моделью к искомым функциям добавляются еще две переменные: кинетическая энергия турбулентности k и скорость диссипации турбулентности ε. Газовой средой является воздух при температуре 20 °С. Наличие каких-либо массовых сил не учитывается.

В рассматриваемой нами задаче число Рейнольдса может достигать значений 105-106, что свидетельствует о турбулентном режиме течения.

Для расчета течения в ВСЗУ используем уравнения Рейнольдса [12]:

d(p«) +дМ +5(pw) = 0 д x    ду     д z

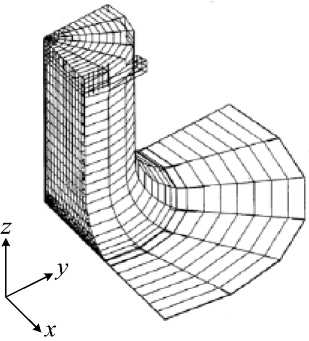
Рис. 2. Расчетная область и направления осей декартовых координат

Fig. 2. Settlement area and directions of axes of the Cartesian coordinates

d ( p uu 8 x	) , d(p uv ) + 5 ( p uw ) = _ d y       d z	^ s d p + ux + uy 8 x 8 x 8 y		я S дт + _ uz 8 z	(3)
d ( p vu d x	), d ( p vv ) , d ( p vw ) = d y P 8 z	8 p дт vx + d y    d x	s + U T v y d y	+ dT vz 8 z	(4)
d ( p wu 8 x	) d( p wv ) a ( p ww ) _ d y       d z	8 p 5T wx + d z   d x	8т s    атЕ dT w y dT wz ■ +       +        , d y    d z		(5)
T ij" =T ij	+ T tj				(6)

^{T j    p} ul u j ,                                                                    ⁽⁷⁾

t напряжения; T ij

–

где р - плотность воздуха; Tj - вязкие напряжения; pu‘u j - турбулентные турбулентные потоки импульса; i, j = 1, 2, 3, для удобства в выражениях (6) и (7), приняты обо- значения и1 = и, и2 = v, u3 = w, x1 = x, x2 = y, x3 = z. Например, т12 = тиу.

Вязкие напряжения определяются по соотношениям

5U тii   2^

д x i

^T j = ^p

,"' + j I

( ^d x j ^д x J

где μ – динамическая вязкость воздуха при нормальных условиях.

Турбулентные потоки импульса обычно представляют в виде произведения градиентов соответствующих осредненных величин на эффективный турбулентный коэффициент переноса:

д uix т   l eff (—^ + -j) - 3 5 y pk,

XjX где цeff- эффективная турбулентная вязкость; k - кинетическая энергия турбулентности; Sj = 0, если г . j, 5j = 1, если i = j.

Выражение для эффективной турбулентной вязкости следующее:

^ff=^+Cцр—, effe где μ – коэффициент динамической вязкости; k – кинетическая энергия турбулентности; ε – скорость диссипации кинетической энергии; Cμ – эмпирическая константа.

Уравнения, которые определяют кинетическую энергию турбулентности и скорость ее диссипации для стандартной k- ε-модели, имеют вид:

d ( p uk ) , d ( p vk ) , d ( p vk ) =A|" ef L d k V4f 8 k VVf d k ]₊ G __{ps     (11)}

8 x       8 y       8 z     8 x la k ^d x I ^d y I ст k 8 y I 8 z la k ^d z I ,

8 ( p u s ) , 8 ( p v s ) , 8 ( p w s ) 8s\ _±|4 f 8s)

⁸ x ⁸ y .x ^.    x J . y . y J

₊A^ef *)+ C i s g - c 2 pi ! + с з G l .

d z ( G_s d z J k         k      p k

Эмпирические константы C _ц = 0.09, о k = 1.0, о_£ = 1.3, C 1 = 1.43, C ₂ = 1.92, C ₃ = 0 для стандартной k- ε-модели взяты из работы Лаундера [11], для модифицированной k- ε-модели Чена-Кима [13] о _k = 0.8, о = 1.15. С 1 = 1.15, С ₂ = 1.9, C ₃ = 0.25.

Скорость генерации турбулентности G такова:

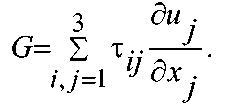
Результаты и обсуждение

Для исследования использовалось устройство (рис. 1), имеющее камеру диаметром d k = 70 mm, диаметр сопел d c = 4 mm, длина сопел l_c = 55 mm, высота камеры H =40 mm, диаметр насадка D = 200 mm. Зазор h менялся от 0.1 до 2.5 mm.

Давление сжатого воздуха на входе в ВСЗУ изменялось от 0.2 до 3 at. При этом расход Q изменялся от 8.5 до 26.5 m3/h.

В ходе расчета было выявлено, что стандартная k -ε-модель турбулентности недостаточно учитывает особенности закрученных течений, так как в результате приводит к значительным отклонениям от экспериментальных данных. Более близкие к экспериментальным результаты дает модифицированная k -ε-модель Чена (см. выше).

На рис. 3–7 в качестве примера представлены только некоторые результаты, полученные теоретически и экспериментально. На рис. 3 и 4 показаны картины скоростей движения воздуха в горизонтальных сечениях зазора между нижней поверхностью устройства и плоскостью пластины 7 . Расстояние z от пластины до рассматриваемого сечения, а также величина зазора h указаны в подрисуночной надписи.

На рис. 3 видно, что в цилиндрической части устройства формируется зона квазитвер-дого вращения, в которой величина тангенциальной скорости возрастает прямо пропор -ционально радиусу. Далее по течению, в области расширения камеры, линейный профиль квазитвердого вращения переходит в параболический (рис. 4) со смещением максимума от стенкикоси.

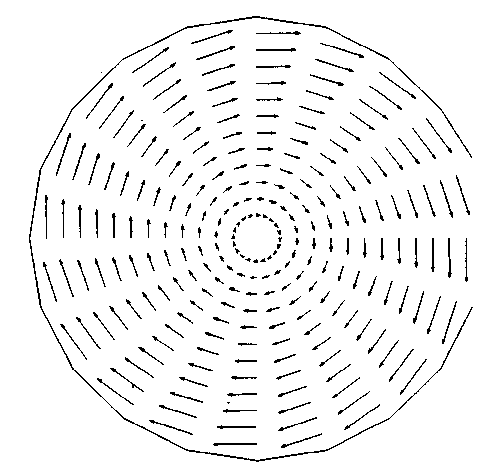
Рис. 3. Поле скоростей в сечении z = 45.8 mm, h = 0.6 mm

Fig. 3. The field of speeds in the section at z = 45.8 mm, h = 0.6 mm

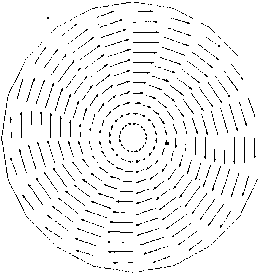
Рис. 4. Поле скоростей в сечении z = 12.75 mm, h = 0.6 mm

Fig. 4. The field of speeds in the section at z = 12.75 mm, h = 0.6 mm

Рис. 5. Поле скоростей в сечении z = 0.45 mm, h = 0.6 mm

Fig. 5. The field of speeds in the section at z = 0.45 mm, h = 0.6 mm

По результатам видно, что радиальная составляющая скорости мала. В области зазора (рис. 5) увеличивается радиальная составляющая скорости, которая все более возрастает при удалении от оси.

На рис. 6 представлены диаграммы зависимости давления в области зазора от радиуса r при разных величинах этого зазора h . Расход составлял 21 m³/h.

При увеличении зазора происходит рост разрежения вблизи центральной оси. При дальнейшем росте до h = 2 mm наблюдается незначительное падение разрежения, однако кривая становится более ровной, без скачков в области, где r ≈ 0.5 mm.

При малых зазорах в этой области этот скачок усиливается, имеется избыточное давление, что вызывает отталкивание пластины. При таких зазорах подъемная сила устройства будет меньше.

На рис. 7 представлено изменение перепада давления от радиуса при зазоре h = 0.6 mm. Точками отмечены экспериментальные значения, пунктиром - расчет с помощью стандартной k –ε-модели, сплошной линией – расчет с помощью модифицированной модели Чена.

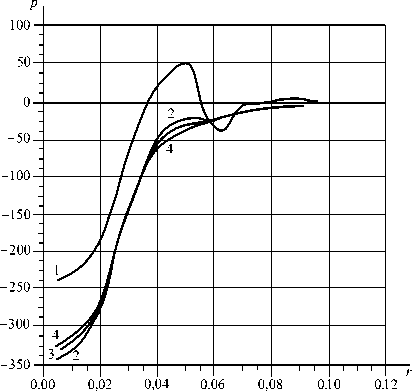
Рис. 6. Зависимость перепада давления (mm H₂O) от радиуса (m) при разном зазоре h (mm): 1 - 0.6; 2 - 1.2;

3 – 1.5; 4 – 2.0

Fig. 6. Dependence of pressure difference (mm H₂O) on radius (m) at a different gap of h (mm): 1 - 0.6; 2 - 1.2;

3 – 1.5; 4 – 2.0

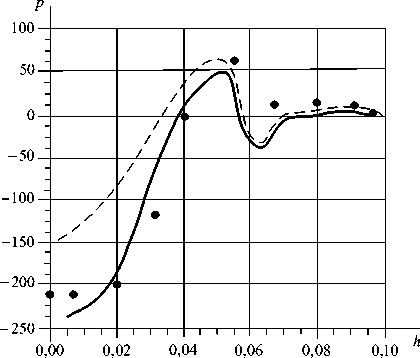
Рис. 7. Зависимость перепада давления (mm H₂O) от радиуса (m) при зазоре h = 0.6 mm (• - эксперимент; сплошная линия – модель Чена; пунктир – стандартная k – ε модель)

Fig. 7. Dependence of pressure difference (mm H₂O) on the radius (m) at h gap = 0.6 mm (• - an experiment; the continuous line – the model Chena; dotted line – standard k – ε model)

Отметим, что обе модели дают близкие к экспериментальным результаты: правильно предсказывают местоположение экстремальных значений, дают близкую схожесть линий. Видно, что модифицированная модель более близка к эксперименту.

Заключение

Результаты исследований показывают, что подъемная (удерживающая) сила повышается по параболическому закону при увеличении давления (расхода) сжатого воздуха, а также не-– 179 – посредственно зависит от геометрических параметров, в частности зазора h. Влияние других параметров пренебрежимо мало и в работе не рассматривалось.

Так, при определенных величинах зазора разрежение, а значит, и подъемная сила оказываются наибольшими. Это позволяет установить на нижней поверхности устройства упоры, удерживающие объект на оптимальном расстоянии.

Наибольшая подъемная сила для данного устройства при давлении на входе 2.8 at и расходе 29.4 m3/h составила 96 N, в этом случае удерживаемый с грузом диск не контактировал с устройством, т.е. зазор устанавливался произвольно.

Данный результат можно улучшить, установив упоры, тогда диск будет прилипать к ним и уже не сможет приблизиться на меньшее расстояние, при котором возникают отталкивающие силы. Использование специальной вставки, позволяющей увеличить радиальные скорости на входе в кольцевую щель (зазор), позволяет значительно увеличить разрежение и подъемную силу.

Таким образом, выполненные экспериментальные и теоретические исследования вихревых струйных захватных устройств показали, что они с успехом могут быть использованы для захвата и транспортирования различных объектов.