Исследование зависимости диаметра ствола на высоте 1,3 м от диаметра пня для сосны обыкновенной в городских посадках на территории г. Хабаровска

Введение. Важной проблемой, имеющей значение для городского зеленого хозяйства, является необходимость восстановления диаметра ствола на высоте 1,3 м по диаметру пня с целью определения величины ущерба в случае нелегального сноса деревьев. На территории г. Хабаровска для этого используется специальная таблица [4]. Данная таблица является частью одноименной таблицы из [6], где сведения, касающиеся сосны обыкновенной, в свою очередь представляют собой преобразованные данные аналогичной таблицы из [7]. В результате анализа используемой таблицы были обозначены следующие моменты:

• 1.    Таблица была разработана на основе исследований стволов деревьев, произрастающих в условиях леса, и предназначена для лесохозяйственных целей на территории Дальнего Востока. Это обстоятельство заставляет задуматься о степени достоверности получаемых результатов при использовании рассматриваемой таблицы в отношении городских насаждений, условия произрастания которых могут создавать существенные различия в сбежистости комлевой части стволов по сравнению с лесными насаждениями.

• 2.    В таблице не учитывается высота пня. Деревья в городской черте нелегально могут спиливаться на различной высоте, в том числе и у шейки корня. Ввиду значительного сбега в комлевой части ствола диаметры пня на различных высотах могут существенно отличаться, следовательно, значения диаметра ствола на высоте 1,3 м, полученные по диаметрам пней, имеющих различную высоту, могут значительно варьировать. Если в лесном хозяйстве имеют место массовые измерения и многими погрешностями можно пренебречь, то городским насаждениям более соответствует индивидуальный подход, что требует использования более точных оценок.

• 3.    Минимальная и максимальная ступени толщины пня в рассматриваемой таблице ограничены значениями 16 и 48 см соответственно, в то время как в городской черте всегда есть деревья (в т.ч. сосны) как меньших, так и больших размеров, и в этом случае не ясно, как определять ущерб от их нелегального сноса. Для сравнения в исходной таблице [6] приводится диапазон диаметра пня от 16 до 76 см, но эти данные по какой-то причине не были использованы.

• 4.    Использование рассматриваемой таблицы ведет к двойному переходу от точного значения диаметра к ступени толщины: один раз для получения ступени толщины пня и второй раз для получения ступени толщины ствола на высоте 1,3 м при определении такс восстановительной стоимости. Двойной переход увеличивает потери информации, что может снижать достоверность результатов.

Исходя из вышесказанного, были поставлены следующие задачи :

• 1.    Разработать регрессионные модели для определения диаметра ствола сосны обыкновенной на высоте 1,3 м по диаметру пня с широким прогнозным диапазоном, для различной высоты пня, применительно к зеленым насаждениям г. Хабаровска.

• 2.    Оценить и сравнить степень достоверности результатов восстановления диаметра ствола на высоте 1,3 м по диаметру пня с использованием разработанных моделей, применяемой таблицы [4], а также других вариантов аналогичных нормативов.

Объекты и методы исследования. В качестве объектов исследования отбирались деревья сосны обыкновенной, произрастающие на территории г. Хабаровска в насаждениях различных структур. Измерения диаметров деревьев производились мерной вилкой в двух взаимно перпендикулярных направлениях с точностью 0,5 см на высотах 0 (шейка корня), 5, 10 и 130 см. Большой массив наблюдений (850 деревьев) был перемешан с помощью генератора равномерно распределенных случайных чисел и методом случайного бес-повторного отбора [2] разделен на две части [3]: выборку для построения регрессионных моделей (549 деревьев) и тестовую выборку для оценки достоверности разработанных моделей и сравниваемых вариантов таблиц (301 дерево). Для аппроксимации зависимостей диаметра ствола на высоте 1,3 м от диаметра пня использовалось уравнение прямой. Ввиду гетероскедастичности регрессионных остатков оценка параметров моделей осуществлялась взвешенным методом наименьших квадратов [1]. Точность моделей, оценка и значимость их параметров, а также выполнение предпосылок регрессионного анализа оценивались соответствующими стандартными методами [1]. Оценка значимости различий между регрессиями, соответствующими различной высоте пня, осуществлялась путем введения фиктивных (dummy) переменных [1]. Регрессионный анализ и сопутствующие ему процедуры статистического оценивания осуществлялись в пакете Statistica 6.

Результаты и их обсуждение. По данным модельной выборки осуществлялся регрессионный анализ зависимостей диаметра ствола на высоте 1,3 м от диаметра пня для трех высот пня (0, 5 и 10 см). Характеристика уравнений регрессии приведена в табл. 1.

Таблица 1

Характеристика уравнений регрессии для зависимостей диаметра ствола на высоте 1,3 м от диаметра пня

h st , см	b		SE b	t	p	R 2	δ	F	p(F)
0	b 0	-0,854	0,190	-4,499	<0,001	0,943	1,975	12085,9	<0,001
	b 1	0,798	0,007	109,936	<0,001
5	b 0	-1,188	0,161	-7,391	<0,001	0,962	1,623	18008,3	<0,001
	b 1	0,846	0,006	134,195	<0,001
10	b 0	-1,164	0,156	-7,454	<0,001	0,968	1,478	20369,8	<0,001
	b 1	0,870	0,006	142,723	<0,001

Примечание: h st – высота пня; b – коэффициент регрессии; SE b – стандартная ошибка коэффициента регрессии; t – расчетное значение критерия Стьюдента; p – расчетный уровень значимости; R² – коэффициент детерминации; δ – стандартная ошибка оценки регрессии; F – значение критерия Фишера значимости регрессии; p(F) – расчетный уровень значимости для F-критерия.

Анализ табл. 1 показывает значимость всех регрессий (p(F) < 0,05). Доля объясненной дисперсии составляет более 94%. Коэффициенты уравнений значимы (p < 0,05). Для оценки значимости различий между зависимостями диаметра ствола на высоте 1,3 м от диаметра пня при различной высоте пня формировалась единая регрессионная модель, в которой влияние высоты пня учитывалось путем введения в уравнение двух бинарных фиктивных переменных (Q 1 и Q 2 ). Тогда регрессионное уравнение имеет следующий вид:

di,3 = bo + bi dst + (p1Qi+ 91Qidst) + (p2Q2+ Ф2Q2dst) + e, где dst – диаметр пня, см;

• Q 1 и Q 2 – фиктивные переменные, определяющие высоту пня;

• μ 1 , μ 2 – коэффициенты, отражающие изменение параметра регрессии b 0 в результате влияния фиктивных переменных;

• φ 1 , φ 2 – коэффициенты, отражающие изменение параметра регрессии b 1 в результате влияния фиктивных переменных.

Для обеспечения возможности сравнения зависимостей d 1,3 = f(d 0 ) и d 1,3 = f(d 0,1 ) с зависимостью d 1,3 = f(d 0,05 ) значения фиктивных переменных были заданы следующим образом: Q 1 = 1 – для высоты пня 0 см; Q 1 = 0 – для высоты пня 5 и 10 см; Q 2 = 1 – для высоты пня 10 см; Q 2 = 0 – для высоты пня 0 и 5 см. Характеристика уравнения регрессии приведена в табл. 2.

Таблица 2

Характеристика уравнения регрессии с фиктивными переменными для зависимости диаметра ствола на высоте 1,3 м от диаметра пня при различной высоте пня

b		SE b	t	p	Adj R2	δ	F	p(F)
b 0	-1,188	0,160	-7,407	<0,001	0,958	1,705	10132,7	<0,001
b 1	0,846	0,006	134,489	<0,001
μ 1	0,334	0,249	1,341	0,180
φ 1	-0,049	0,010	-5,062	<0,001
μ 2	0,024	0,224	0,106	0,916
φ 2	0,024	0,009	2,715	0,007

Примечание: Adj R2 – коэффициент детерминации, скорректированный на число степеней свободы.

В результате анализа табл. 2 можно заключить, что зависимости d 1,3 = f(d 0,05 ) и d 1,3 = f(d 0 ) не имеют значимых различий между свободными членами регрессий (p(μ 1 )>0,05), но значимо различаются коэффициентами наклона (p(φ 1 )<0,05). Различия между зависимостями d 1,3 = f(d 0,05 ) и d 1,3 = f(d 0,1 ) аналогичны (p(μ 2 )>0,05; p(φ 2 )<0,05). В связи с этим рассматриваемые зависимости следует считать статистически значимо различающимися друг от друга. График зависимости диаметра ствола на высоте 1,3 м от диаметра пня по разработанной регрессионной модели приведен на рисунке.

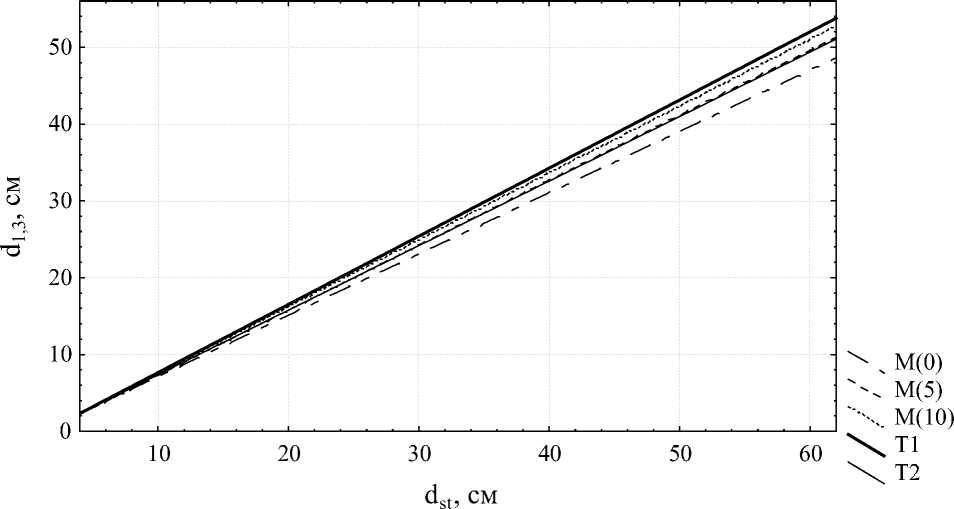
Зависимости диаметра ствола на высоте 1,3 м от диаметра пня (разработанная модель и сравниваемые варианты): M(0) – модель для h st = 0 см; M(5) – модель для h st = 5 см; M(10) – модель для h st = 10 см; T1 – таблица из [6]; T2 – таблица А.М. Межибовского [5]

В качестве вариантов нормативов для сравнения с полученной моделью были выбраны табл. из [6] (исходный вариант для табл. из [4]) и табл. А.М. Межибовского [5], по данным которых построены прямые, также изображенные на рисунке. В качестве критерия достоверности принималась относительная частота совпадений ступеней толщины фактических значений диаметра ствола на высоте 1,3 м со значениями, найденными по модели (или табл.) по фактическим значениям диаметра пня. Величина ступени толщины принималась равной 4 см в соответствии с существующей градацией для такс восстановительной стоимости деревьев в насаждениях г. Хабаровска [4]. Высота пня задавалась как фиксированной для всех наблюдений выборки, так и произвольной, выбираемой случайным образом из рассматриваемых вариантов высот (0, 5 или 10 см). Случайный выбор высоты пня позволяет имитировать практическое использование модели для пней различной высоты. В свою очередь, выбор фиксированной высоты пня позволяет определить достоверность модели при условии ее использования для заданных высот пня. Результаты расчетов сведены в табл. 3.

Анализ табл. 3 показывает, что соответствие между значениями диаметра ствола на высоте 1,3 м, полученными по разработанной модели, и фактическими значениями наблюдается в 63,2–69,4% случаев (в зависимости от высоты пня и режима (случайный или фиксированный) ее выбора. Наряду с расхождениями на одну ступень толщины, при использовании модели возможны расхождения на две ступени в 0,3–2,6% случаев. Расхождений на три ступени толщины не выявлено. Ярко выраженного дисбаланса между относительной частотой завышений и занижений значений не наблюдается.

Соответствие между значениями диаметра ствола на высоте 1,3 м, полученными по таблице из [6], и фактическими значениями наблюдается в 44,0–62,1% случаев. Наряду с расхождениями на одну ступень толщины возможны расхождения на две ступени в 0,7–10,5% случаев. Для высоты пня 0 см возможны также расхождения на три ступени толщины – в 1,4% случаев. Кроме того, выявлено, что при использовании таблицы частота завышений значений диаметра ствола на высоте 1,3 м значительно превышает частоту занижений (в 1,7–9,6 раза). Достоверность разработанной нами модели выше, чем достоверность данной таблицы, на 7,3–19,2%.

Таблица 3

Относительные частоты расхождений между фактическими значениями диаметра ствола на высоте 1,3 м и его значениями, полученными по разработанной модели и по таблицам сравниваемых вариантов

Вариант сравнения	Предлагаемая модель							Таблица из [6]							Таблица А.М. Межибовского [5]
h st , см	0
∆d 1,3 , см	+4	-4	+8	-8	+12	-12	0	+4	-4	+8	-8	+12	-12	0	+4	-4	+8	-8	+12	-12	0
γ, %	17,6	16,6	2,3	0,3	0	0	63,2	38,8	5,3	10,5	0	1,4	0	44,0	25,6	10,6	4,0	0	1,0	0	58,8
h st , см	5
∆d 1,3 , см	+4	-4	+8	-8	+12	-12	0	+4	-4	+8	-8	+12	-12	0	+4	-4	+8	-8	+12	-12	0
γ, %	16,6	14,3	1,3	0	0	0	67,8	31,3	8,6	4,0	0	0	0	56,1	15,6	16,6	1,7	0,7	0	0	65,4
h st , см	10
∆d 1,3 , см	+4	-4	+8	-8	+12	-12	0	+4	-4	+8	-8	+12	-12	0	+4	-4	+8	-8	+12	-12	0
γ, %	15,3	15,0	0,3	0	0	0	69,4	23,0	14,2	0,7	0	0	0	62,1	8,6	23,6	0,3	1,3	0	0	66,2
h st , см	0, 5 или 10 (случайный выбор)
∆d 1,3 , см	+4	-4	+8	-8	+12	-12	0	+4	-4	+8	-8	+12	-12	0	+4	-4	+8	-8	+12	-12	0
γ, %	17,6	15,3	1,0	0	0	0	66,1	28,8	9,5	6,6	0	0	0	55,1	17,9	16,3	1,3	1,3	0	0	63,2

Примечание: ∆d 1,3 – величина расхождения; γ – относительная частота расхождения.

Соответствие между значениями диаметра ствола на высоте 1,3 м, полученными по таблице из [5], и фактическими значениями наблюдается в 58,8–66,2% случаев. Наряду с расхождениями на одну ступень толщины возможны расхождения на две ступени в 1,6–4,0% случаев. Для высоты пня 0 см возможны расхождения на три ступени толщины – в 1% случаев. Дисбаланс между относительной частотой завышений и занижений значений диаметра ствола на высоте 1,3 м проявляется по-разному в зависимости от высоты пня:

при случайном выборе высоты пня и при использовании таблицы для высоты пня 5 см – не прослеживается; при использовании таблицы для высоты пня 0 см наблюдается преобладание частоты завышений над частотой занижений в 7,7 раза; при использовании таблицы для высоты пня 10 см, наоборот, наблюдается преобладание частоты занижений над частотой завышений – в 2,8 раза. Достоверность результатов восстановления диаметра ствола на высоте 1,3 м по диаметру пня при использовании таблицы из [5] выше, чем при использовании таблицы из [6], на 4,1–14,8%. Результаты оценки разработанной нами модели и таблицы из [5] в целом близки: достоверность модели выше на 2,4–4,4%.

Выводы

• 1.    Таблица зависимости диаметра ствола на высоте 1,3 м от диаметра пня, используемая в настоящее время на территории г. Хабаровска [4], для сосны обыкновенной в диапазоне высот пня от 0 до 10 см имеет достоверность результатов 44,0–62,1%, допускает ошибки на две ступени толщины в 0,7–10,5% случаев и на три ступени толщины (при высоте пня 0 см) – в 1,4% случаев, дает систематические завышения результатов, имеет ограниченный диапазон диаметров пня (16–48 см), в связи с чем значительно уступает по тем же показателям аналогичной таблице А.М. Межибовского [5] и еще больше – разработанной нами модели.

• 2.    Предлагаемая модель дает большую достоверность результатов по сравнению с применяемой таблицей [4] для высот пня до 10 см на 7,3–19,2%. Частота расхождений на две ступени толщины при использовании модели сведена к минимуму. Модель сбалансирована по частоте положительных и отрицательных отклонений и может использоваться для деревьев сосны в диапазоне диаметров пня от 5 до 58 см.

• 3.    Прямолинейные зависимости диаметра ствола на высоте 1,3 м от диаметра пня для сосны обыкновенной в городских посадках Хабаровска для высот пня 0, 5 и 10 см статистически значимо различаются в коэффициентах наклона (p ≤ 0,007). Высота пня оказывает значимое влияние на рассматриваемые зависимости, в связи с чем должна учитываться при разработке соответствующих нормативов, что позволит существенно повысить степень достоверности получаемых результатов.