Исследование зависимости константы кюри суспензии суперпарамагнитных наночастиц от индукции магнитного поля

В ранее опубликованных экспериментальных работах [1–3] статические магнитные восприимчивости суспензий суперпарамагнитных наночастиц находили путем интегрирования значений дифференциальных магнитных восприимчиво-стей, определяемых электромагнитным методом при нескольких частотах, и экстраполяции к нулевой частоте. При этом было получено, что экспериментальные зависимости статических магнитных восприимчивостей от термодинамической температуры Т на начальных участках кривых намагничивания подчиняются закону Кюри— Вейсса. В работе [4] показано, что если намагниченность суспензии J находить по формуле J = В / µ0– Н, где В и Н — индукция и напряженность магнитного поля внутри суспензии, то ее магнитная восприимчивость χ = J µ0 / B на начальном участке кривой намагничивания (при малых В) подчиняется закону Кюри χ = С / Т. Это дает возможность, измеряя χ при неизвестной термодинамической температуре Т, определять эту температуру по формуле Т = С / χ. Константу Кюри С можно найти по формуле С = Тт χт, измерив магнитную восприимчивость χт при температуре Тт тройной точки воды. Для практического применения метода измерения температуры нужно знать, в каком диапазоне индукций магнитного поля В выполняется закон Кюри, т. е. константа Кюри не зависит от В. Теоретически закон Кюри следует из формулы Ланжевена J = Jн La(ξ), где La — функция Ланжевена, Jн — намагниченность насыщения, ξ = р В / (k T) — параметр Ланжевена, р — магнитный момент наночастицы. Отсюда

С = J µ 0 T / B = C 0 3 La( ξ ) / ξ ,        (1)

где

С 0 = J н р µ 0 / (3 k )                   (2)

есть значение С при ξ << 1.Теоретическая зависимость С / С 0 от ξ , построенная по формуле (1), приведена на рисунке кривой 1. Ее нужно сравнить с экспериментальной зависимостью С от индукции В .

ЭКСПЕРИМЕНТ

Для проведения экспериментальных исследований зависимости константы Кюри от магнитной индукции была применена установка, описанная в работе [5]. Исследуемая суспензия представляла собой коллоидный раствор в воде наночастиц магнетита с весовой концентрацией твердой фазы 14 %. Суспензия помещалась в два одинаковых цилиндрических контейнера диаметром 20 и высотой 45 мм, которые располагались вертикально на расстоянии 4 мм друг от друга во внешнем магнитном поле с индукцией В 0 , создаваемой системой постоянных магнитов и направленной перпендикулярно плоскости, проходящей через оси обоих контейнеров. В щели между контейнерами и вблизи нормальной В ₀ торцевой поверхности одного из них расположены 1-я и 2-я радиочастотные катушки для измерения методом ЯМР напряженности Н и индукции В магнитного поля внутри суспензии.

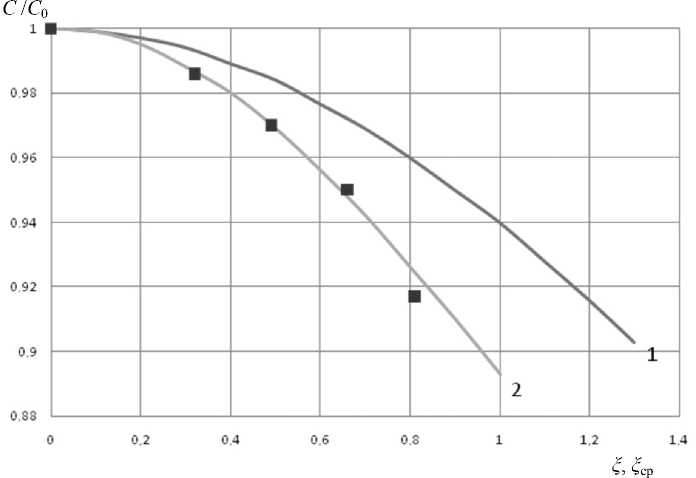
Теоретические и экспериментальная зависимости константы Кюри С суспензии суперпарамагнитных наночастиц от магнитной индукции.

1 — теоретическая зависимость С от ξ без учета полидисперсности наночастиц; 2 — теоретическая зависимость С от усредненных значений ξ ср с учетом полидисперсности наночастиц. Экспериментальная зависимость представлена экспериментальными точками

Экспериментальные результаты определения константы Кюри С. ( ξ ср — усредненное значение параметра Ланжевена)

Установив при отсутствии контейнеров некоторое значение индукции В 0 , при котором частоты ЯМР, измеренные в обеих катушках, равны f 0 = γ в ⋅ B 0 ( γ в = 4.25 ⋅ 10⁷ — гиромагнитное отношение в единицах Гц/Тл), помещают на свои штатные места контейнеры с исследуемой суспензией и измеряют частоты ЯМР f 1 и f 2 в 1-й и 2-й катушках. По этим частотам находят напряженность Н = γ н f 1 и индукцию В = γ в f 2 магнитного поля внутри суспензии ( γ н = 53.4 — гиромагнитное отношение в единицах Гц ⋅ м/А). Константу Кюри определяют по формуле С = (1 – f 1 / f 2 ) T .

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

В таблице приведены полученные экспериментально значения константы Кюри С при нескольких индукциях магнитного поля В, определяемых по частотам f2. Значение С = С0 найдено усреднением 7 значений С, полученных при В < 10 Гс. Для сравнения экспериментальных результатов, приведенных в таблице, с теоретической кривой 1 на рисунке, нужно связать значения индукций В со значениями параметра Ланжевена ξ = р В / (k T). Для этого необходимо знать значение магнитного момента наночастиц р. Магнитный момент р можно найти из формулы (2), подставив в нее экспериментальное значение С0 = 171.6 К из таблицы и намагниченность насыщения Jн = 8100 А/м, полученную в работе [5]. В результате получается р = 7⋅10–19 Дж/Тл. При таком значении магнитного момента для каждой экспериментальной точки, приведенной в таблице, находим параметры Лан-жевена ξ, приведенные в 4-й строке таблицы. С использованием этих параметров и значений С, приведенных в таблице, получаем экспериментальные точки, отмеченные в виде квадратиков на рисунке. Можно убедиться, что экспериментальные точки не ложатся на теоретическую кривую 1.

Причина может быть в распределении наночастиц по размерам, приводящим к различию их магнитных моментов. Приняв эту гипотезу, введем функцию распределения наночастиц по параметрам Ланжевена ξ — f(ξ) — и напишем выражение для намагниченности суспензии с учетом to этого распределения : J = Jн J La(c) f (^)d^ .

Для оценки константы Кюри С = J µ 0 T / B примем распределение наночастиц по значениям их магнитных моментов равномерным от 0 до максимального значения р м . При этом среднее значение магнитного момента наночастицы р ср = р м / 2, распределение наночастиц по параметрам ξ равномерно от ξ = 0 до максимального значения ξ м = = p м B / ( k T ) = 2 p ср B / ( k T ) и функция распределения f ( ξ ) = 1 / ξ м . Произведя интегрирование, получаем:

С = ( J н µ 0 Т / В ξ м ) ln(Sh( ξ м ) / ξ м ) =

= (6 С 0 / ξ м ²) ln(Sh( ξ м ) / ξ м ),                (3)

где С 0 = J н µ 0 p м / (6 k ) = J н µ 0 p ср / (3 k ), что с учетом равенства р = р ср совпадает с (2). Теоретическая зависимость С / С 0 от усредненного параметра Ланжевена ξ ср = р ср В / ( k T ) = ξ м / 2, построенная по выражению (3), приведена на рисунке кривой 2. Можно убедиться, что приведенные на рисунке экспериментальные точки лежат на кривой 2, построенной с учетом полидисперсности наночастиц, из чего можно сделать вывод, что скорость уменьшения константы Кюри с ростом В зависит от полидисперсности наночастиц. Это можно использовать для оценки полидисперсности суперпарамагнитных наночастиц.

ЗАКЛЮЧЕНИЕ

На основании полученных результатов можно сделать следующее заключение.

• 1.    Для уменьшения зависимости константы Кюри от магнитной индукции нужно применять суспензию суперпарамагнитных наночастиц с близкими размерами.

• 2.    По зависимости константы Кюри от магнитной индукции можно оценивать функцию распределения суперпарамагнитных наночастиц по размерам.