Исследование зависимости плотности кремнеземных нетканых волокнистых материалов от величины удельной нагрузки

Автор: Струк А.А., Медведев А.В., Разумеев К.Э.

Журнал: Вестник Витебского государственного технологического университета @vestnik-vstu

Рубрика: Технология материалов и изделий текстильной и легкой промышленности

Статья в выпуске: 1 (47), 2024 года.

Бесплатный доступ

В статье представлены результаты исследования зависимости плотности кремнеземных нетканых волокнистых материалов от величины удельной нагрузки. Нетканые волокнистые материалы в виде матов широко применяются в различных отраслях промышленности. Материалы для теплоизоляции металлургического и энергетического оборудования производятся в виде иглопробивных матов и иглопрошивных матов с облицовкой из термостойких тканей. Особое место среди волокнистых материалов занимают теплоизоляционные высокотемпературные кремнеземные материалы. Рассмотрены волокнистые маты их холстов механического и аэродинамического формирования. Материал волокнистых холстов - кремнеземные волокна КВ-11 диаметром 7,5 мкм длиной 60 мм. Из части холстов на иглопробивной машине выработаны иглопробивные маты. Холсты механического способа формирования имеют выраженное ориентированное положение волокон. В связи с этим для экспериментов были подготовлены образцы матов из холстов с продольной и продольно - поперечной ориентацией волокон. Образцы с продольно - поперечной ориентацией собирались в пакет через один слой. Методика проведения эксперимента по исследованию зависимости изменения плотности кремнеземных нетканых волокнистых матов от удельной нагрузки заключалась в определении толщины образцов при нагружении образцов грузами. Иглопробивные маты имеют более стабильные параметры при сжимающих нагрузках, чем маты из холстов механического способа формирования. Однако низкая исходная плотность иглопробивных матов может привести к дополнительным затратам для достижения заданных значений плотности теплового экрана. Плотность тепловых экранов должна находиться в пределах 100-200 кг/м3. Из имеющихся на рынке волокнистых материалов с указанными выше параметрами для теплового экрана выбраны иглопробивные маты Суперсилика плотностью от 120 до 170 кг/м3. Проведенные исследования показали, что коэффициент корреляции между удельной нагрузкой и изменением толщины в процентах от начальной толщины образцов выше для образцов из матов Суперсилика. В связи с этим использование иглопробивных матов Суперсилика в тепловых экранах с двухсторонней облицовкой из кремнеземной ткани более предпочтительно.

Еще

Нетканые материалы, иглопробивные маты, иглопрошивные маты, удельная нагрузка, плотность нетканых материалов

Короткий адрес: https://sciup.org/142241258

IDR: 142241258 | DOI: 10.24412/2079-7958-2024-1-9-20

Текст научной статьи Исследование зависимости плотности кремнеземных нетканых волокнистых материалов от величины удельной нагрузки

DOI:

Article info: received June 15, 2023.

The article was prepared based on the report of the International Scientific and Technical Conference "International Conference on Textile and Apparel Innovation ICTAI–2023".

Нетканые волокнистые теплоизоляционные материалы (ТИМ) производятся в виде иглопробивных матов и иглопрошивных матов с облицовкой из термостойких тканей. Одним из основных параметров ТИМ является плотность. Исследованию влияния плотности на механические и теплофизичекие свойства волокнистых нетканых материалов посвящен ряд работ (Киселев, 2010; Леденева, Кирсанова, Севостьянов и Белгородский, 2023; Лисиенкова, Комарова и Проскуряков, 2021; Луговой, Бабашов и Карпов 2014; Маскайкин и Махров, 2021; Сергеенков и Захаров, 2006; Сергеенков и Захаров 2008; Chen Zhou, Zhijin Wang and Paul M. Weaver, 2017; Gumen et al., 2001; Maqsood et al., 2000; Ma, Pan, Li and Deng, 2023).

В работах (Киселев, 2010; Леденева, Кирсанова, Севостьянов и Белгородский, 2023; Лисиенкова, Комарова и Проскуряков, 2021; Луговой, Бабашов и Карпов, 2014; Сергеенков и Захаров, 2006; Сергеенков и Захаров, 2008; Ma, Pan, Li and Deng, 2023) рассмотрены процессы сжатия волокон в массе и построены диаграммы деформирования материала при деформации сжатия. При этом наблюдается существенная зависимость вида диаграммы от плотности деформируемого материала. В работе (Луговой, Бабашов и Карпов, 2014) показано, что при температуре 1000–1200 °С при установившемся тепловом потоке интенсивность нагрева «холодной» пластины выше для волокнистого материала с плотностью 100 кг/м3, чем для материала с плотностью

200 кг/м3. Для ТИМ еще одним из параметров является коэффициент теплопроводности. На основании зависимостей коэффициента теплопроводности от температуры и плотности материала сделан вывод, что менее плотные материалы в области температур ниже 1000–1200 °С имеют коэффициент теплопроводности более низкий, чем более плотные (Луговой, Бабашов и Карпов, 2014). В работах (Маскайкин и Махров, 2021; Chen Zhou, Zhijin Wang and Paul M. Weaver, 2017; Gumen et al., 2001, Maqsood et al., 2000) исследованы зависимости коэффициента теплопроводности от удельной нагрузки на волокнистый материал. Увеличение удельной нагрузки с 0,6 до 9,66 кПа приводит к увеличению коэффициента теплопроводности на 45 %.

Анализ публикаций показал, что волокнистые материалы под действием сжимающей нагрузки изменяют плотность и свои свойства в значительно большей степени, чем другие текстильные материалы.

Целью работы является исследование зависимости изменения плотности кремнеземных нетканых волокнистых матов от удельной нагрузки.

Нетканые волокнистые материалы представлены иглопрошивными и иглопробивными матами. Основой волокнистых матов является холст механического или аэродинамического способа формирования. В связи с этим объектами исследования зависимости плотности кремнеземных нетканых волокнистых матов от удель- ной нагрузки являлись кремнеземные маты из холстов механического способа формирования, кремнеземные иглопробивные маты из холстов механического и аэродинамического способа формирования.

Холсты механического способа формирования выработаны на чесальной машине ЧМТ из кремнеземных штапельных волокон марки КВ-11(7,5) ТУ 5952-18405786904-2004 производства АО «НПО Стеклопластик». Длина штапеля 60 мм, диаметр волокна 7,5 мкм. Поверхностная плотность холстов от 114 до 235 г/м2. Заданная поверхностная плотность достигалась сгущением прочеса после съема виброгребнем со съемного барабана чесальной машины. На рисунке 1 представлены штапельное волокно (а) и холст механического способа формирования (б).

Выработанные холсты имеют выраженное ориентированное положение волокон. В связи с этим для экспериментов были подготовлены образцы матов из холстов с продольной и продольно-поперечной ориентацией волокон. Образцы с продольно-поперечной ориентацией собирались в пакет – через один слой. Из части холстов выработаны иглопробивные маты на иглопробивной машине в ООО «Ниагара».

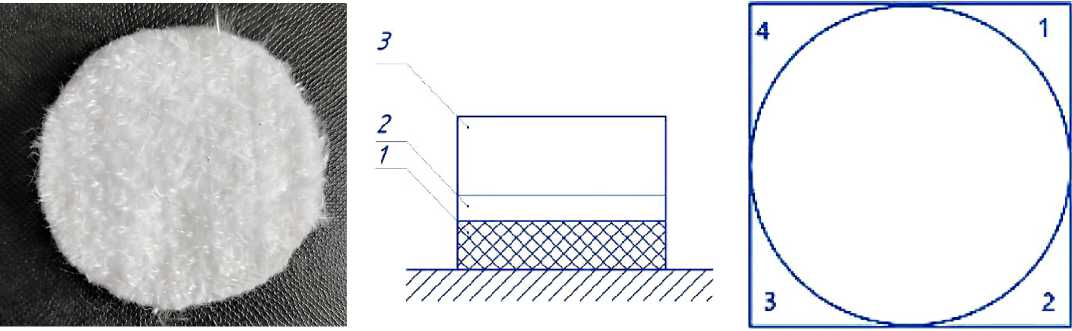
Отбор и подготовку образцов матов для испытаний проводили в соответствии с ГОСТ 15902.2-2003 и ГОСТ 12203-2003. Испытания образцов проводили на экспериментальном стенде в условиях свободного сжатия образцов. Образцы для испытаний диаметром 56 мм вырезались пробойником. На рисунке 2 (а) представлена фотография образца иглопробивного мата, на рисунке 2 (б) представлено схематическое изображение экспериментального стенда (1 – образец; 2 – пластина, 3 – груз), на рисунке 2 (в) представлена схема измерения толщины образцов.

Толщина образцов измерялась перед началом испытаний штангенрейсмасом типа ШРЦ ГОСТ 164-84 с ценой деления, равной 0,05 мм в центре образца без приложения сжимающей нагрузки. Количество слоев в пакете, ориентация волокон и свойства матов из холстов механического способа формирования представлены в таблице 1.

Количество слоев в пакете, ориентация волокон и свойства иглопробивного мата из холстов механического способа формирования представлены в таблице 2.

Методика проведения эксперимента по исследованию зависимости изменения плотности кремнеземных нетканых волокнистых матов от удельной нагрузки заключалась в определении толщины образцов при нагружении образцов грузами. Среднее значение толщины образцов получены по результатам измерений в четырех точках пластины (рисунок 2 в). Толщина, удельная нагрузка и плотность матов из холстов механическо-

аб

Рисунок 1 – Штапельное волокно (а) и холст механического способа формирования (б) Figure 1 – Staple fiber (a) and mechanically formed canvas (b)

абв

Рисунок 2 – Образец иглопробивного мата (а), схематическое изображение экспериментального стенда (б), схема измерения толщины образцов (в) Figure 2 – Sample of needle-punched mat (a), schematic representation of experimental stand (b), scheme of sample thickness measurement (c)

Таблица 1 – Количество слоев в пакете, ориентация волокон и свойства матов из холстов механического способа формирования

Table 1 – Number of layers in the package, fiber orientation and properties of mats made of canvas by mechanical forming method

Номер образца	Ориентация волокон в образах	Количество слоев в пакете		Толщина, мм	Поверхностная плотность, г/м²	Плотность, кг/м³
Номер образца	Ориентация волокон в образах	Продольных	Поперечных	Толщина, мм	Поверхностная плотность, г/м²	Плотность, кг/м³
1	Продольная	3	нет	14,05	344,36	24,51
2	Продольнопоперечная	2	1	18,95	480,76	25,37

Таблица 2 – Количество слоев в пакете, ориентация волокон и свойства иглопробивного мата из холстов механического способа формирования

Table 2 – Number of layers in the package, fiber orientation and properties of needle-punched mat from mechanically formed canvases

Номер образца	Ориентация волокон в образах	Количество слоев в пакете		Толщина, мм	Поверхностная плотность, г/м²	Плотность, кг/м³
Номер образца	Ориентация волокон в образах	Продольных	Поперечных	Толщина, мм	Поверхностная плотность, г/м²	Плотность, кг/м³
3	Продольная	3	нет	32,1	757,95	23,61
4	Продольнопоперечная	2	1	30,25	736,46	24,34

Таблица 3 – Количество слоев в пакете, ориентация волокон и свойства иглопробивного мата из холстов механического способа формирования

Table 3 – Thickness, specific load and density of mats made of mechanically formed canvases

Удельная нагрузка, кПа	Толщина, мм		Плотность, кг/м³
	Номер образца		Номер образца
	1	2	1	2
1,98	5,50	9,58	63,27	76,73
3,96	3,90	5,80	89,23	126,84
4,91	2,60	4,38	133,85	168,35
5,94	2,10	3,96	165,71	185,78
6,89	1,90	3,79	183,16	194,62
10,86	1,80	3,68	193,33	200,46
14,82	1,56	3,61	223,08	195,30

Таблица 4 – Толщина, удельная нагрузка и плотность иглопробивных матов из холстов механического способа формирования

Table 4 – Thickness, specific load and density of needle-punched mats made of mechanically formed canvases

Удельная нагрузка, кПа	Толщина, мм		Плотность, кг/м³
	Номер образца		Номер образца
	3	4	3	4
1,98	17,11	16,7	44,30	44,09
3,96	10,64	9,5	71,24	77,51
4,91	6,95	6,85	109,06	107,49
5,94	6,04	5,44	125,49	135,35
6,89	5,65	5,1	134,15	144,38
10,86	4,75	4,59	159,57	160,42
14,82	4,35	4,13	174,24	178,29

Таблица 5 – Свойства иглопробивных матов Суперсилика

Table 5 – Properties of needle-punched mats Supersilika

Наименование	Марка	Толщина, мм		Плотность, кг/м³
Наименование	Марка	До испытаний	По НТД	До испытаний	По НТД
Иглопробивной мат Суперсилика	С 6	6,95	6	125,95	140
	С 10	11,25	10	106,47	150
	С 20	23,55	20	137,6	170

Таблица 6 – Толщина, удельная нагрузка и плотность иглопробивных матов Суперсилика

Table 6 – Thickness, specific load and density of needle-punched mats Supersilika

Удельная нагрузка, кПа	Толщина, мм			Плотность, кг/м³
	Номер образца			Номер образца
	5	6	7	5	6	7
1,98	16,20	22,5	19,6	162,54	122,23	157,96
3,96	14,20	17,10	19,05	191,78	166,25	162,52
4,91	11,18	15,05	13,86	235,53	241,99	223,37
5,94	10,16	12,2	12,47	259,17	271,31	248,27
6,89	8,57	8,83	10,57	307,26	289,33	292,90
10,86	7,86	8,28	10,37	335,01	310,72	298,55
14,82	7,48	7,71	8,83	352,03	329,53	350,62

Таблица 7 – Изменение толщины от удельной нагрузки в процентах от начальной толщины образцов

Table 7 – Thickness variation with specific load as a percentage of the initial thickness of the specimens

Удельная нагрузка, кПа	Номер образца
Удельная нагрузка, кПа	1	2	3	4	5	6	7
1,98	50,96	45,91	53,76	56,56	41,29	53,51	74,27
3,96	33,31	23,80	36,7	35,17	37,17	42,09	57,49
4,91	26,76	19,47	24,23	22,98	30,12	38,31	51,85
5,94	26,33	18,26	22,54	19,97	27,82	34,71	48,20
6,89	25,09	17,47	21,55	18,68	26,47	32,80	44,88
10,86	22,95	16,89	19,71	15,70	26,47	30,58	42,29
14,82	22,06	16,25	19,43	14,38	25,34	29,67	41,38

Таблица 8 – Коэффициент корреляции между удельной нагрузки и изменением толщины в процентах от начальной толщины образцов

Table 8 – Correlation coefficient between specific load and thickness change as a percentage of the initial thickness of the specimens

Номер образца
1	2	3	4	5	6	7
-0,7264	-0,6467	-0,7183	-0,7521	-0,7783	-0,82048	-0,80186

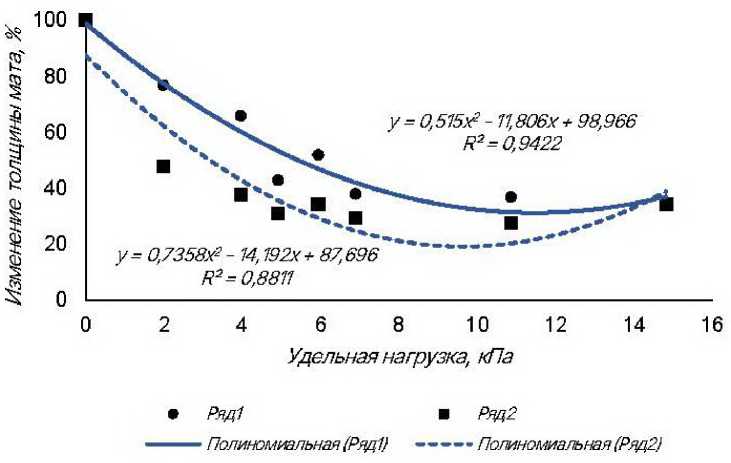
Рисунок 5 – Зависимость изменения толщины волокнистого теплового экрана и волокнистого мата Суперсилика от удельной нагрузки в процентах от исходной толщины мата

Figure 5 – Dependence of the change in thickness of the fiber heat shield and Supersilika fibrous mat on the specific load as a percentage of the initial mat thickness

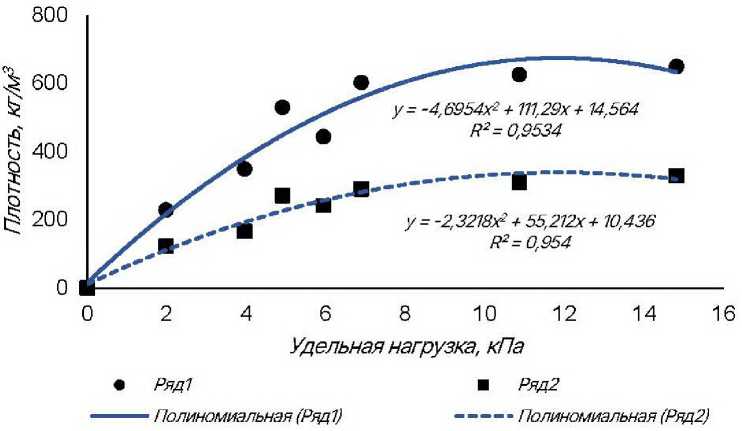
Рисунок 6 – Зависимость плотности теплового экрана и волокнистого мата Суперсилика от удельной нагрузки

Figure 6 – Dependence of the density of the heat shield and Supersilika fiber mat on the specific load

4. Исходя из проведенных исследований использование иглопробивных матов Суперсилика в тепловых экранах с двухсторонней облицовкой из кремнеземной ткани более предпочтительно.

Список литературы Исследование зависимости плотности кремнеземных нетканых волокнистых материалов от величины удельной нагрузки

Киселев, А.М. (2010). Математическое моделирование процесса сжатия волокнистых материалов в массе, Известия ВУЗов. Технология текстильной промышленности, № 5, С. 14-17.
Леденева, И.Н., Кирсанова, Е.А., Севостьянов, П.А., Белгородский, В.С. (2023). Особенности диссипации энергии деформации в валяльно-войлочном материале. Известия ВУЗов. Технология текстильной промышленности, № 1, С. 84-90.
Лисиенкова, Л.Н., Комарова, Л.Ю., Проскуряков, Н.Е. (2021). Исследование деформации нетканых материалов в условиях циклического сжатия. Известия ТулГУ. Технические науки. Вып. 4. С. 31-38.
Луговой, А.А., Бабашов, В.Г., Карпов, Ю.В. (2014). Температуропроводность градиентного теплоизоляционного материала, Труды ВИАМ: электронный научно-технический журнал, № 2. [Электронный ресурс]. - Режим доступа: https://viam-works.ru/plugins/content/joumal/uploads/articles/pdf/642.pdf - Дата доступа: 04.06.2023.
Маскайкин, В.А., Махров, В.П. (2021). Исследование теплопроводности многослойной теплоизоляционной обшивки летательных аппаратов в условиях полета. Вестник Московского авиационного института, Т 28. № 4. С. 118-130.
ООО «РЛБ Силика». [Электронный ресурс]. - Режим доступа: https://supersilika.ru/rlb-qsilikaq/prodam, дата обращения [04.06.2022].
Сергеенков, А.П., Захаров, А.А. (2006). Анализ степени сжатия наполнителя на деформационные свойства холстопрошивных полотен. Известия ВУЗов. Технология текстильной промышленности, № 6, С. 77-79.
Сергеенков, А.П., Захаров, А.А. (2008). Анализ степени сжатия наполнителя на деформационные свойства холстопрошивных полотен. Известия ВУЗов. Технология текстильной промышленности, № 3, С. 75-77.
Chen Zhou, Zhijin Wang and Paul M. Weaver. Thermal-Median^al Optimization of Folded Core Sandwidi Panels for Thermal Prate^on Systems of Space Vehides. International Journal of Aerospace Engineering, Volume 2017 (online), a^ess from https://doi.org/10.1155/2017/3030972.
Gumen V., Maqsood A. et al. (2001). Higt-Temperature Termal Condu^ty of Ceram^ Fibers, Journal of Materials Engineering and Performance, Volume 10(4), 475.
Intelligent Materials Pvt. Ltd. [Электронный ресурс]. - Режим доступа: http://www.nanoshel.com, дата обращения [04.06.2022].
JPS Composite Material. [Электронный ресурс]. - Режим доступа: https://jpscm.com/products/astroquartz/, дата обращения [03.07.2023].
Maqsood Asghari, Gumen Vadim, et al. (2000), Thermal conductivity of ceramic fibres as a funrtion of temperature and press load, Journal of Physics D: Applied Physics, Volume 33 (16), p. 2057-2063.
Q.H. Ma, R. Pan, J.P. Li and H.P. Deng (2022). Study on Dynamo Pressure Control of Air-Breathing Hypersonio Vehide. International Symposium on Advanced Launch Technologies (ISALT 2022). Journal of Physics: Conference Series 2460 (2023) 012040 IOP Publishing doi: 10.1088/1742-6596/2460/1/012040.

Еще

Статья научная