Исследование жесткости и собственных частот колебаний платформы манипулятора

Выделим из общей схемы пространственного механизма оригинальную часть, реализующую угловые движения вокруг осей X и Y и поступательное перемещение вдоль оси Z за счет сложения двух встречных вращений [1, с.248]. Традиционные три связи (две поступательных и одно вращение) опустим, поскольку они реализованы в серийном оборудовании и их жесткость достаточно известна (рис. 1).

Наиболее неблагоприятное нагружение связей будет, если исключить из расчетной схемы, параллельно действующие элементы, образуемые приводными устройствами a, b и с. Поэтому основу жесткости конструкции будет составлять жесткость их соединений, а именно сдвоенные шарниры.

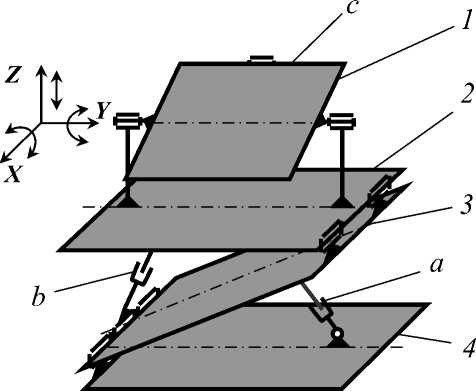
Рис. 1. Расчетная схема оригинальной части пространственного манипулятора: 1-установочное звено (рабочий стол); 2- опорно-поворотное устройство; 3- наклонная платформа; 4- поворотный стол; a,b,c- приводные устройства (ШВП, гидроцилиндры)

Для решения поставленной задачи используем зависимости, приведенные в [2, с.632]. При взаимном сжатии равномерно распределенной нагрузкой q двух цилиндров, соприкасающихся параллельными образующими (рис. 2). При E 1 = E 2 = E полуширина полоски контакта b, учитывая, что q = P/l , будет:

b = 1,522 ⋅

P R ⋅ R

⋅

\ l ⋅ E R - R

где q - распределенная нагрузка, E1, E2 и R1, R2 - модули упругости материалов и радиусы первого и второго цилиндров, соответственно.

Наибольшее напряжение, действующее в точках оси площадки, будет:

(Г

max

0,418 •

P • E R — R ----------------- • -------------------------

\ l R_x • R₂

Приведенные выше формулы получены при значении коэффициента Пуассона μ=0,3 .

Сближение соприкасающихся тел, т.е. цилиндров определяется по формуле:

P z _

A = 1,82 • — • (1 - In b )                      (3)

l • E

Из выражения (2) видно, что при малой разности (R 2 - R 1 ) , т.е. когда (R 2 - R 1 )→0 будет:

• 1)    из выражения (1): b^ да ;

• 2)    из выражения (2): σ max →0.

Это говорит о том, что если контакт между цилиндрами будет полным, зазоры отсутствуют, наибольшие напряжения будут иметь минимальные значения.

Зная усилие P на цилиндры и их сближение Δ, можно рассчитать жесткость данного сопряжения:

P       P           lE

Тогда c = — =------------=-------- или окончательно:

^A 1,82[1 — ln b ]   ^{1,82[1 — ln} b ^]

, lE c =

lE

1,82[1 — ln f 1,522 I — • R ¹ ^ R ²

1 /F R - R

^        ^lE R 2   ^R 1 J

—

]

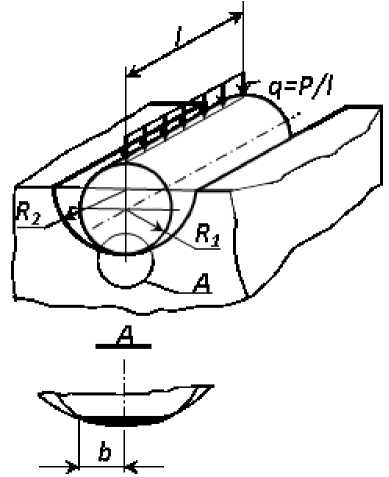
Рис. 2. Контакт цилиндра с цилиндрической впадиной

Рассчитаем коэффициенты жесткости при следующих параметрах модели:

l = 5∙10-2 м, Е = 2∙1011Па; R1=4,9∙10-3 м; R2=5∙10-3 м; Усилие P будем варьировать: Р1 = 102 Н, Р2 = 103 Н, Р3 = 104 Н, Р5 = 105 Н, Р6 = 106 Н.

Расчеты приводят к следующим значениям:

с 1 =5,236∙10⁸ Н/м, с 2 =5,881∙10⁸ Н/м, с 3 =6,708∙10⁸ Н/м, с 4 =7,805∙10⁸ Н/м, с 5 =9,331∙10⁸ Н/м                                                        (5)

Кроме того, надо учесть, что в предлагаемом схемном решении такие спряжения (их 3 ед.) соединены последовательно, поэтому надо перевести жесткость в податливость и определить её приведённое значение:

с ' С2 ' с откуда находим:        с =-----1—2—3---- (6)

С • с ₂ + С • с ₃ + с ₂ • с₃

Для упрощения принимаем с = с 1 = с 2 = с 3 , тогда формула (6) перепишется как:

с пр = С                                          (7)

Используя расчетные значения жесткости (5):

(сmin...сmax)=(5,236∙108... 9,331∙108) Н/м по формуле (7) находим:

(с пр.min …c пр.max )=(1,745∙10⁸…3,110∙10⁸) Н/м

В [3, с.193] показано, что жесткость суппортов станков средних размеров составляет (30…100) Н/мкм или с супп. ст . = (3∙10⁷…10⁸) Н/м.

Рассматривая схемное решение оригинального манипулятора как колебательную систему, определим качественный параметр этой системы -собственную частоту её колебаний k. Из теории колебаний [4, с.26], известно, что собственная частота k колебаний зависит только от параметров системы и определяется как:

k = —. К 2n a a

Здесь a - коэффициент инерции системы. В нашем случае a=m, с_пр -приведенная жесткость системы, m - масса системы.

Используя, ранее рассчитанные значения, спр и задавая значения массы m: m1=10 кг, m2=20 кг, m3=30 кг, найдём собственные частоты системы, по выражению (8), сведя их в таблицу 1:

Таблица 1

cпр.i , Н/м m i , кг	1,745∙108	1,960∙108	2,236∙108	2,601∙108	3,110 ∙108
10	665 Гц	705 Гц	752,6 Гц	812 Гц	888 Гц
20	470 Гц	498,2 Гц	532 Гц	574 Гц	627,6 Гц
30	384 Гц	407 Гц	434,5 Гц	469 Гц	512,4 Гц

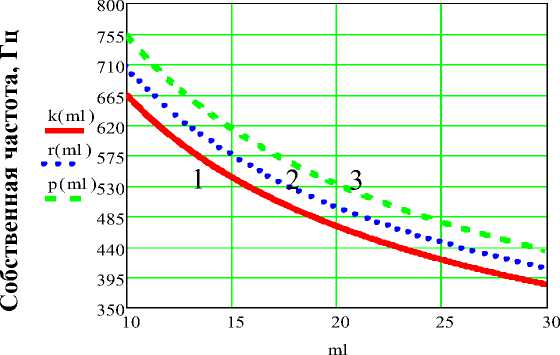
Сравнивая полученные значения с эксплуатационными частотами технологического оборудования [5, 6] видно, что оборудование, оснащенное предлагаемым манипулятором, будет работать в дорезонансной зоне. Используя пакет программы MathCAD 15, приводим графические зависимости выражения (8) в зависимости от массы m системы и приведённой жесткости с пр , которые представлены на рис. 3 и рис. 4.

c1 := 1.74510 8    c2 := 1.96010 8     c3 := 2.23610 8

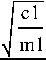
2п

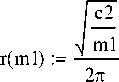
P(m1) :=

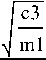
2п

k(ml) :=

Масса, кг

Рис. 3. Зависимость собственных частот колебаний от приведенной массы системы: кривая 1 при с пр =1,745∙10⁸ Н/м , кривая 2 при с пр =1,960∙10⁸Н/м , кривая 3 при с пр =2,236∙10⁸ Н/м

m1:= К m2:= 20 m3:= 30

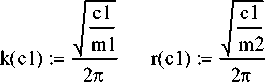
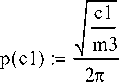
cl

Приведённая жесткость, Н/м

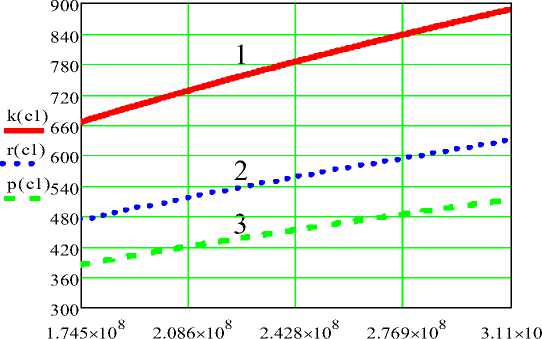
Рис. 4. Зависимость собственных частот колебаний от приведенной жесткости системы: кривая 1 при m=10 кг , кривая 2 при m=20 кг , кривая 3 при m=30 кг

Выводы:

• 1)    Результаты расчетов приведенной жесткости показали, что жесткость предложенной модели оригинального манипулятора сравнима с жесткостью суппортной группы станков средних размеров.

• 2)    Диапазон собственных частот предлагаемой конструкции манипулятора выше эксплуатационных частот силового возбуждения технологического оборудования.

• 3)    Предлагаемое техническое решение механизма манипулятора рекомендуется к использованию в технологических машинах машиностроительных производств.