Исследование зубчато-рычажного механизма прерывистого вращательного движения с внешним зацеплением колес

Исполнительные органы некоторых машин совершают движения с остановками, длительность которых зависит от требований технологического процесса. Например, подача ткани на швейной машине зигзагообразной строчки производится при помощи кулачково-рычажного механизма. Наличие высших кинематических пар и появление ударов не позволяет использовать указанный механизм при высоких скоростях.

Лучшие динамические характеристики имеет зубчато-рычажный механизм с внутренним зацеплением зубчатых колес, результаты исследований которого представлены в работах [1]-[3]. Рассмотрим возможность применения в указанных условиях зубчато-рычажного механизма с внешним зацеплением колес, схема которого представлена на рис. 1. Механизм состоит из неподвижного зубчатого колеса 1, водила 2 и сателлита 3, который имеет палец 4 с установленным на нем камнем 5, образующим поступательную пару с кулисой 6, имеющей общую ось вращения с водилом. При вращении водила движение пальца через камень передается кулисе 6, совершающей прерывистое вращательное движение.

Рисунок 1 - Схема зубчато-рычажного механизма

Координаты пальца:

x = L • cos а - l cos в ; y = L sin а - l sin в ,

где L=OA (рис. 1); l=AB ; a - угол поворота водила; в — угол поворота сателлита. Углы а и в связаны между собой зависимостью [4]:

I R

в = I —+1 а, V r У где R и r- радиусы делительных окружностей центрального колеса и сателлита.

Обозначим l = K • r , где К - коэффициент.

Тогда

IR x = (R + r) • cos а - kr cosI — +1 |а;

V r У

I R y = ( R + r ) sin а - kr sin I —+ 1 | а .

V r У

Так как угловые характеристики механизма ф , ш и е не зависят от абсолютных

R размеров механизма, то принимая r=1 и учитывая, что — = U , получим:

r x = (U +1) • cos а - k cos(U + 1)а;

y = ( U + 1) sin а - k sin ( U + 1 ) а ,

Угловое перемещение кулисы:

y ф = arctg—                                 (4)

x

При исследовании механизма приняты U=1^5 и К=1^1,5. На рис. 2 представлен график углового перемещения кулисы для случая, когда U=2 и К=1,2. На графике через ао обозначен угол поворота кулисы за время приближенной остановки, в течение которого кулиса имеет некоторое перемещение фо. Величина этого перемещения характеризует стабильность остановки кулисы и составляет для рассматриваемого случая 2,30 при ао=41,40. Это означает, что кулиса имеет остановку, равную 23% времени цикла, соответствующего половине оборота водила.

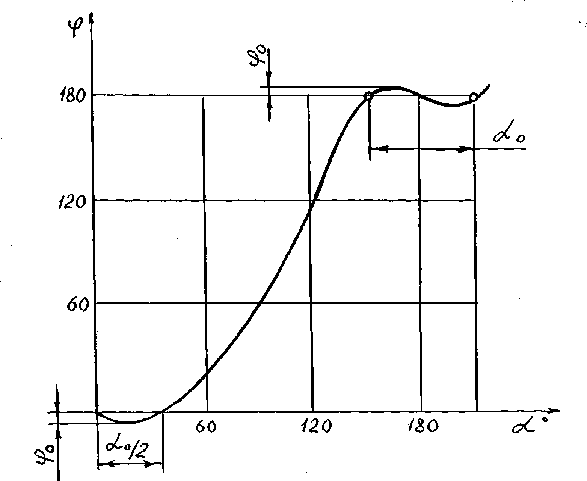
Рисунок 2 – График углового перемещения кулисы в зависимости от угла поворота водила

На рис. 3 представлены графики изменения длительности α о и стабильности φ о остановки кулисы в зависимости от величины К .

Как показали исследования, кривые изменения φ о и α о в зависимости от коэффициента К имеют вид парабол. Уравнение кривой изменения φ о имеет вид:

Ф о = a ( k - 1) n ,                                       (5)

где а – коэффициент; n – показатель степени.

Подставляя в это уравнение по два любых значения φ о и К , получим два уравнения с двумя неизвестными, из которых определим а и n . Тогда

Ф о = 23,5( k - 1)^1,4.                                    (6)

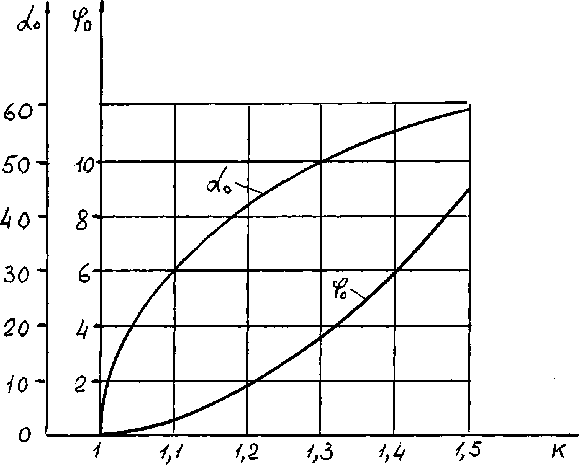
Рисунок 3 – Графики изменения длительности и стабильности остановки кулисы

Аналогично

a o = 90V k - 1 ,

отсюда

a

K = --+ 1 .

Длительность и стабильность остановки при различных значениях К можно оценить аналитически. На рис. 4 представлена траектория движения пальца камня во время остановки кулисы, к которой проведена касательная из начала координат, совпадающего с осью вращения кулисы. Скорость пальца в точке касания направлена по касательной, расположенной под углом φ о к горизонтальной оси α .

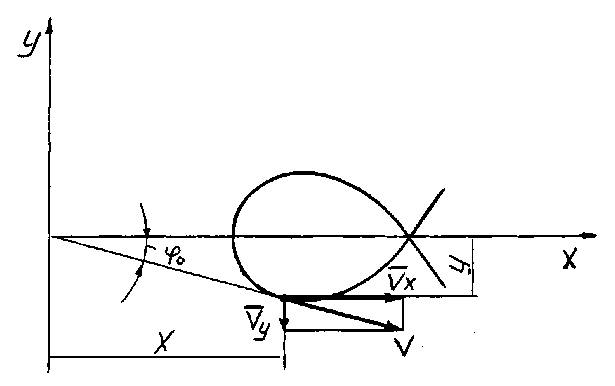
Рисунок 4 – Траектория движения пальца во время остановки кулисы

Угловое перемещение кулисы:

Учитывая, что a=wt и дифференцируя уравнения (3), получим: x = -to (U + 1) sin a + k to (U + 1) sin[( U + 1) a ]

y = to (U + 1)cos a - k to (U + 1)cos[( U + 1) a ] ’

Из (10) с учетом (3) и (11) имеем:

a = — arccos

U

U + 1 + K

K (U + 2)

В качестве примера проведем оценку длительности и стабильности остановки кулисы при U=2 и К=1,2 . Из уравнений (12) и (9) имеем а=11,1⁰ и ф_о=2,4⁰ . На рис. 2 представлен график углового перемещения кулисы, из которого видно, что при движении кулисы из начального положения (при ф=0 ) а= а 0 /2 . Для рассматриваемого случая ( U=2)

y = 3sin a - K sin3 a = 0

Учитывая, что sin3 a = 3sin a - 4sin³ a , получим:

3sina - K(3sina - 4sin3 a) = 0 (13), отсюда

a = arcsin 0,867

K - 1

K

Из (14) при К=1,2 имеем а=20,7⁰ . Тогда а_о=41,4⁰, что соответствует ранее найденному значению α о .

Полученные аналитические зависимости применимы при расчете и проектировании аналогичных механизмов. Задаваясь величиной α о , которая берется из циклограммы работы машины, по формуле (8) находим значение К , а затем из уравнения (6) определяем угол φ о отклонения кулисы за время кажущейся остановки и оцениваем его с точки зрения технологического процесса.