Исследования коэффициента трения. Вывод аналитического уравнения диаграммы Герси-Штрибека

Благодарности. Работа выполнена при финансовой поддержке РФФИ, Правительства Красноярского края и Красноярского краевого фонда науки в рамках гранта № 20–42–240015 p_a_ Красноярск.

Цитирование: Дамдинов Б. Б. Исследования коэффициента трения. Вывод аналитического уравнения диаграммы Герси-Штрибека / Б. Б. Дамдинов, Ч. М. Митыпов // Журн. Сиб. федер. ун-та. Техника и технологии, 2022, 15(7). С. 835–849. DOI: 10.17516/1999-494X-0439

и заменить внешнее трение внутренним, которое определяется только вязкостью смазки и значительно меньше внешнего. В современном мире наука о маслах пошла как по пути усовершенствования нефтяных смазок путем введения в них различных добавок, так и по пути создания синтетических смазочных материалов.

Физический контакт деталей приводит к изнашиванию поверхностей трения, возникающих при перемещении тел относительно друг друга. Физические явления, сопровождающие процесс механического контакта, существенно влияют на потребительские свойства машин и могут приводить к отказам в работе. Следовательно, основная задача – предотвращение изнашивания материалов, одним из которых является применение смазочного материала.

Смазка определяется как некоторый процесс, в результате которого уменьшаются трение и износ трущихся поверхностей за счет применения смазочного материала. В качестве смазочных материалов могут использоваться как газообразные и жидкие, так и твердые материалы [1]. Нахождение зависимости силы трения (вязкости) от скорости скольжения, что принято называть коэффициентом трения, является важной проблемой при решении практических задач. Механизм действия смазки в узлах машин и различных механизмов достаточно сложен. Сложность заключается в ряде причин: жидкие смазочные материалы изменяют свойства под действием нагрузочной силы, с другой стороны, твердые узлы трения тоже претерпевают изменения под влиянием нагрузки и смазки. Ранние работы по природе действия смазочного материала исследовали такие ученые, как Кузнецов В. Д., Ахматов А. С., Рамайя К. С., Крагель-ский И. В. и др. [2].

В настоящей работе будет исследован коэффициента трения в зависимости от вязкости и условий пользования – скорости и погонной нагрузки в узлах трения. Реология жидких смазок является важнейшим свойством их применения, поскольку от них зависят износ, потери мощностей механизмов и машин, эффективность двигателей и многие другие факторы. Систематизации теоретических и экспериментальных знаний относительно влияния физических параметров применения на реологию смазочного материала в данный момент нет. Например, в настоящее время испытание на трение чаще всего проводят с длительной приработкой трущихся поверхностей в различных режимах работы, приближенных к реальным условиям. При этом реализуются различные типы трения; меняются физические свойства смазочного материала и самих поверхностей трения, и цельной картины поведения материалов получить не удается [6]. В работе [7] исследовано влияние адгезии (глубины индентирования), которая в первую очередь зависит от площади контакта. Показано, что при наличии адгезии коэффициент трения пропорционален площади контакта трущихся поверхностей.

1.    Коэффициент трения и его связь с вязкостью

Свойства смазочных материалов, как и коллоидных растворов, зависят от концентрации, природы дисперсной фазы и растворителя, что отражается в величине сил межмолекулярных взаимодействий веществ в растворах. Эти взаимодействия могут иметь физическую природу (силы Ван дер Ваальса) и сложную физико-химическую природу: водородную и ионномолекулярную связь, комплексы с переносом заряда и др. Наряду с процессами, происходящими в смазочном материале, за счет интенсивной работы в узлах трения образуются частицы износа, которые также могут влиять на характеристики смазочного материала.

Установлено, что сила жидкостного трения при использовании смазочного масла с дисперсными компонентами в подшипниках скольжения и качения выражается аналогично обобщённому уравнению А. Эйнштейна (Симха-Эйнштейна) [8]:

Як = ЕКДс(1 + М^ (1)

где F _жд_с - сила жидкостного трения при использовании смазочного масла без дисперсных компонентов, ф - объемная доля дисперсной фазы, а - эмпирическая константа, зависящая от формы частиц.

Как было показано выше, для описания зависимости вязкости от концентрации в умеренно концентрированных устойчивых к агрегации дисперсных системах наиболее широкое распространение получили уравнения, выведенные с использованием теории Эйнштейна в приближении непрерывности фазы. Физический смысл уравнения (1) заключается в том, что относительное приращение вязкости прямо пропорционально относительному содержанию дисперсной фазы. Чем больше ф , тем сильнее выражено тормозящее влияние частиц (не обладающих внутренней текучестью) на поток. Из теории Эйнштейна следует, что разбавленные и устойчивые дисперсные системы являются ньютоновскими жидкостями, их вязкость линейно связана с объёмной долей дисперсной фазы и не зависит от дисперсности [9]. Обзор различных мелкодисперсных добавок к смазочным материалам, в том числе и модификаторам трения, представлен в работе [11].

Уравнение Эйнштейна не подходит при прямом моделировании опор скольжения в смазочном материале. Численные методы исследования, а также экспериментальные данные показывают, что с началом относительного движения трущихся тел шероховатости обеих поверхностей интенсивно разрушаются и деформируются. Возникает выраженный граничный слой, в котором происходит процесс деформации и обратный эффект восстановления разрушенных элементов, а также их перемешивания. Для расчета механизмов, работающих при разных режимах и видах трения, используется зависимость силы (коэффициента) трения от скорости относительного движения трущихся поверхностей. При динамическом моделировании опор скольжения обычно используют [1] закон вязкого трения Ньютона для взаимодействующих через слой смазки коаксиально расположенных цилиндров:

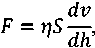
где S – площадь соприкасающихся слоев жидкости, h – толщина граничного слоя, η – вязкость смазочного материала, v – относительная скорость сдвига трущихся поверхностей. Заметим, что толщина граничного слоя может изменяться в зависимости от приложенной нагрузки [12]. Также следует учитывать, что вязкость может быть нелинейным параметром (неньютоново-ская жидкость) и зависеть от скорости сдвига [13]. В этом случае закон вязкого трения Ньютона носит неудовлетворительный характер.

На основании сведений об особенностях работы того или иного механизма или узлов трения с добавлением смазочного материала можно выявить определенные закономерности в целесообразности и надежности их использования. При изменении скорости происходит переход одного режима трения в другой, о чем наглядное представление дает диаграмма Герси-

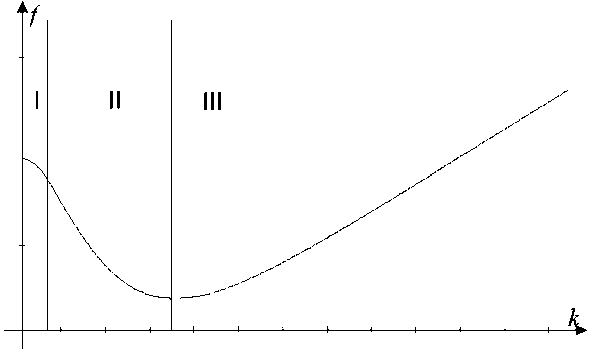
Рис. 1. Диаграмма Герси-Штрибека

Fig. 1. Hersey-Shtribek diagram

Штрибека, представляющая собой зависимость коэффициента трения f от характеристики к , так называемое число Герси (рис. 1)

Аналитическое уравнение числа Герси (Гумбеля) выглядит следующим образом:

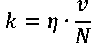
где v – скорость относительного перемещения трущихся тел, N – погонная нагрузка на узел трения. Для случаев непоступательного движения пар трения вместо скорости сдвига берется угловая скорость относительного вращения. С увеличением числа Герси существенно меняются реализуемые режимы трения. Область I соответствует положению, когда смазочного материала на поверхности трения чрезвычайно мало и между трущимися поверхностями реализуется сухое или близкое к нему трение (граничное трение). На участке II реализуется так называемое смешанное трение, при котором происходит адаптация смазочного материала к нагрузкам. Наиболее низкое трение реализуется в условиях, когда на поверхностях трения образуются слои поверхностно-активных веществ (модификаторы трения), входящих в смазку, строго ориентированные друг относительно друга и со слабым сопротивлением скольжению по плоскостям их контактирования. В этом случае проявляются свойства неньютоновской вязкости смазочного материала. С дальнейшим увеличением слоя жидкости в зоне трения (зона III) начинает реализовываться жидкостной или вязкий режим трения, при котором коэффициент трения постепенно повышается по мере увеличения числа Герси [15].

По мнению авторов работы по трибологии и особенностям кривых Герси-Штрибека, в научной литературе отсутствует анализ изменения относительного положения кривых в зоне жидкостной смазки для масел с различными молекулярными массами в случае учета вязкости как варьируемого параметра, тогда как изучение этого явления представляет не только научный, но и практический интерес [17]. Для анализа междисциплинарной природы трения, акцентируя внимание на обобщенных, термодинамических моделях, в работе [19] прилагается энергетическая интерпретация процессов, происходящих при трении в узлах машин и меха-– 839 – низмов. Такая модель оказывается плодотворной и позволяет широко анализировать закономерности внешнего трения.

2.    Анализ данных диаграммы Герси – Штрибека.Вывод аналитического уравнения

Начальным этапом определения характеристик трения является экспериментальное исследование реологических свойств смазочного материала, затем на основе экспериментальных данных строятся аналитические приближения (аппроксимации). Данный алгоритм исследования является наиболее распространенным и используется во многих областях промышленности. Есть и другой метод, по которому возможно определить вязкостные характеристики вещества – при наличии хорошей теории выражаются математические зависимости, которые сравниваются с аналитическими приближениями. Этот путь является более актуальным, так как предоставляется возможность моделировать поведение различных смазочных материалов в зависимости от характеристик самого вещества и механизмов, обеспечивающих вязкое трение. Заметим, что диаграмма Герси – Штрибека (рис. 1) является графиком, построенным на основе экспериментальных данных, и нахождение его аналитического уравнения позволило бы определить поведение смазочного материала без проведения эксперимента.

Самое первое аналитическое уравнение было предложено Амонтоном в 1608 году, затем было уточнено Кулоном в 1875 году:

F = А + fN ,                                                         (4)

где F - сила трения, f - безразмерный коэффициент, N - сила нормального давления (прижимная сила), A – эмпирическая константа. Эта зависимость была установлена экспериментально для тел, совершающих поступательное движение при скольжении относительно неподвижной поверхности. Значение коэффициента трения f , который находится экспериментально, зависит от физико-механических свойств смазочных материалов и состояния трущихся поверхностей в зоне контакта – их чистоты, наличия пленки или смазки, температуры.

При формулировке своей биноминальной формулы Кулон первоначально утверждал о независимости силы трения от скорости скольжения, что было подтверждено им опытным путем. Однако при дальнейшем увеличении скорости скольжения это опровергалось. В конце XVIII века итальянскому ученому Конти удалось установить зависимость коэффициента трения от скорости скольжения. Приведенные замечания о коэффициенте трения означают, что проводимые расчеты с использованием закона Кулона не могут претендовать на высокую точность. Тем не менее получаемые результаты, как правило, являются вполне достаточными для инженерной практики. Следует отметить, что поступательное движение пар трения является обязательным условием использования формулы Кулона-Амонтона [20].

На приведенных графиках (рис. 2) представлены зависимости силы трения от скорости сдвига: а – показывает закон Кулона – Амонтона, б – показывает уменьшение коэффициента трения по гиперболическому закону, в - степенная (квадратичная) зависимость силы трения F ( v ” ), г - линейная зависимость коэффициента трения. Заметим, что график (рис. 2а) отличается наличием скачка в силе трения при отсутствии скорости сдвига, что также может иметь место при других зависимостях. Степенная зависимость в основном используется при описании сухого (гранично -

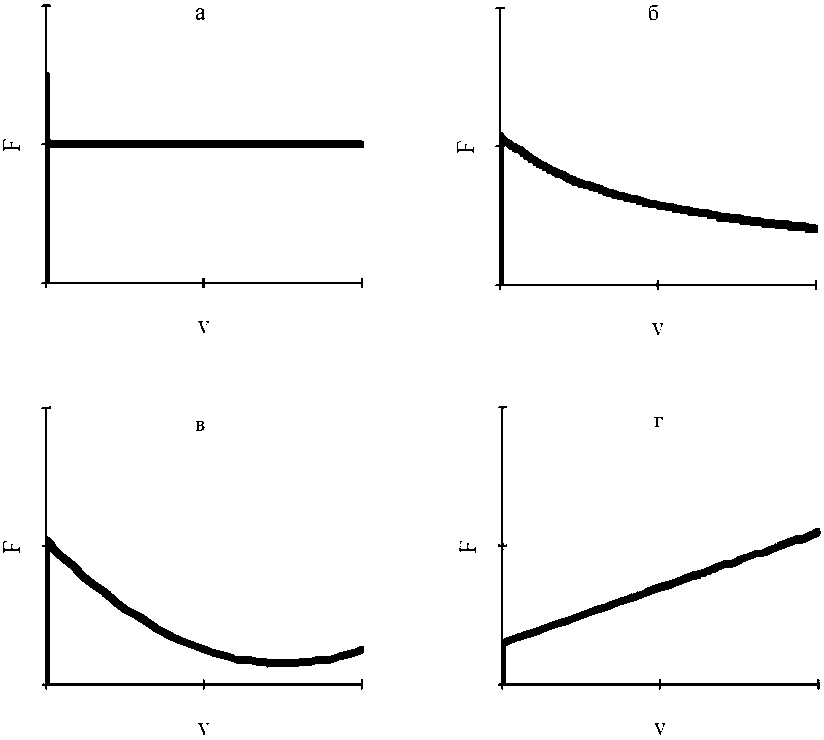
Рис. 2. Различные модели коэффициента трения (пояснения в тексте)

Fig. 2. Various models of the coefficient of friction (explanations in the text)

го) трения. Линейная характеристика присуща уже установившемуся, вязкому трению. Следует отметить, что при описании классических систем (маятник Фроуда, тормозная колодка, модель Ван дер Поля), наибольшее применение получила параболическая зависимость (рис. 2в). Более подробный анализ закона Кулона – Амонтона, описывающий сухое трение, приведен в работе [22]. Авторами работ [20] говорится о том, что применение параболической зависимости выбрано из-за удобства вычислений, без объяснения его физического смысла.

Некоторые сведения о функциональной зависимости коэффициента трения можно получить, используя анализ размерностей. Заметим, что коэффициент трения является безразмерной величиной, следовательно, он может получиться только при тех параметрах, комбинация которых составляет безразмерную величину. При исследовании трения нагруженных подшипников с помощью формулы вязкости Ньютона была получена формула коэффициента трения гидростатических опор скольжения:

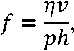
Это соотношение впервые вывел профессор Н. П. Петров, опубликовавший в 1883 г. свою статью под названием «Трение в машинах и влияние на него смазывающей жидкости» [23].

При п = const , p = const , h = const данная формула приобретает линейную зависимость (прямая Петрова), которая может быть использована при описании зоны III на диаграмме Герси – Штрибека (рис. 1).

Для математического описания остальных зон (зона I и II) на кривой Герси – Штрибека была предложена эмпирическая формула [5]:

f = (а + hv)e '^l/ + d , (6)

где a , b , c , d - константы, зависящие от природы тел и условий трения. Анализ уравнения показывает, что первое слагаемое функции стремительно убывает и само значение коэффициента трения стремится к константе d . Это утверждение справедливо при сухом граничном трении, но при добавлении жидкого смазочного материала (не исключается возможность добавления твердой смазки) коэффициент трения должен увеличиваться по мере возрастания скорости трения. Ранее предложенная формула Петрова как раз и показывает зависимость коэффициента трения при больших скоростях относительно перемещения трущихся тел. Тогда с помощью замены переменной d на формулу (6) мы получим следующее выражение:

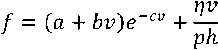
Для подробного анализа коэффициента трения для этих зависимостей были построены графики (рис. 3):

Как и следовало ожидать, замена константы d приводит к тому, что при больших скоростях трущихся тел коэффициент трения приобретает линейную зависимость. С большой точностью можно определить границы сухого, смешанного и жидкостного трения, что позволяет говорить о том, что с помощью уравнения (7) можно описать диаграмму Герси-Штрибека. Дальнейший анализ этого выражения, в которое входит определение остальных эмпирических констант, а также влияние типов смазочного материала на коэффициент трения позволит моделировать различные условия – экстремальные нагрузки, сверхнизкие и высокие температуры, добавление присадок и т.д.

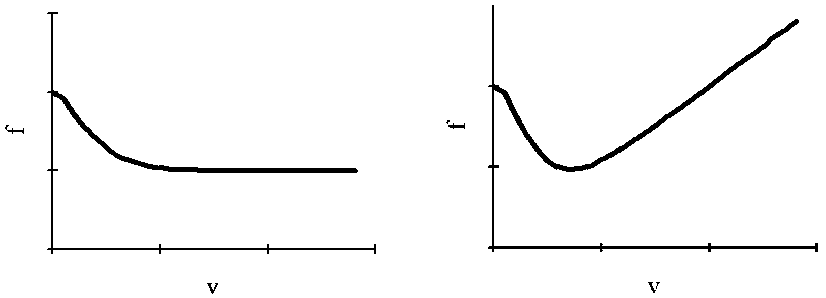
Рис. 3. Коэффициенты трения, построенные с помощью уравнения (6) – слева, уравнения (7) – справа

Fig. 3. Friction coefficients constructed using equation (6) – on the left, equation (7) – on the right

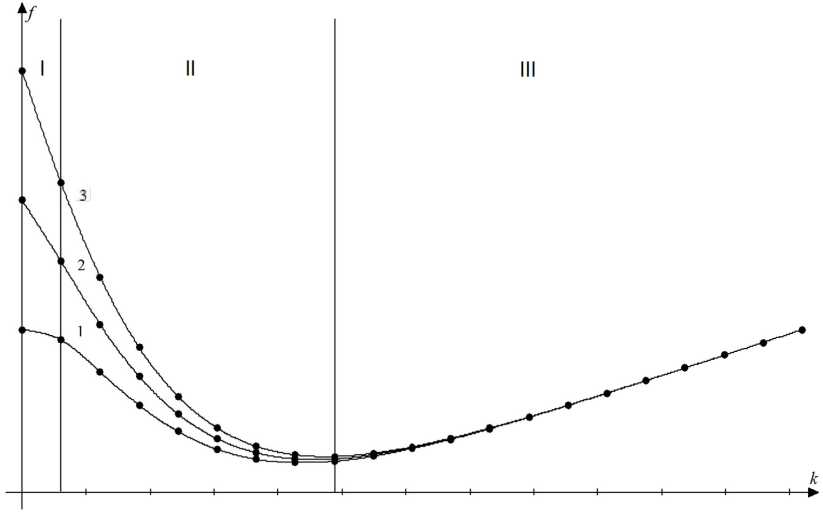
Рис. 4. Изменение коэффициента a при b, c, η, p, h – const

Fig. 4. Change of the coefficient a at b, c, n, p, h - const

Уравнение (7) состоит из суммы двух функций с одинаковыми аргументами, в данном случае скорости скольжения. Как мы выяснили ранее, функция nvIph характеризует уже установившееся, жидкостное трение. Очевидно, что первая функция характеризует граничное и смешанное трение. В этой функции находятся несколько эмпирических постоянных, и с помощью вариации этих констант (т.е. изменение одной константы, помимо остальных) было выяснено, что коэффициент a отвечает за начальное трение (трение покоя). Для наглядности был построен график с различными коэффициентами а (рис. 4). Построенные зависимости характеризуют трение от самого низкого значения константы a до самого высокого – кривая 1, затем кривая 2, далее кривая 3. Важно отметить, что такая последовательность будет использоваться и для других графиков. Соответственно, чем больше начальное трение (трение покоя), тем больше коэффициент a . Заметим, что при возрастании коэффициента граница между зоной I и II становится менее отчетливой. Анализ размерностей говорит о том, что параметр а является безразмерной величиной, соответственно, можно его принять за коэффициент трения покоя.

Для определения физического смысла коэффициента b также были построены кривые при различных константах (рис. 5). На рисунке видно, что по мере возрастания величины b пик максимума силы трения становится больше. Положение максимума на кривой зависит от давления и от твердости каждого из трущихся тел. Численные методы исследования, а также экспериментальные данные показывают, что с началом относительного движения трущихся тел шероховатости обеих поверхностей интенсивно разрушаются и деформируются, что приводит к изменению коэффициента трения. Возникает выраженный граничный слой, в котором происходит процесс деформации и обратный эффект восстановления разрушенных элементов, а также их перемешивания. Следовательно, по мнению автора, коэффициент b характеризует такие – 843 –

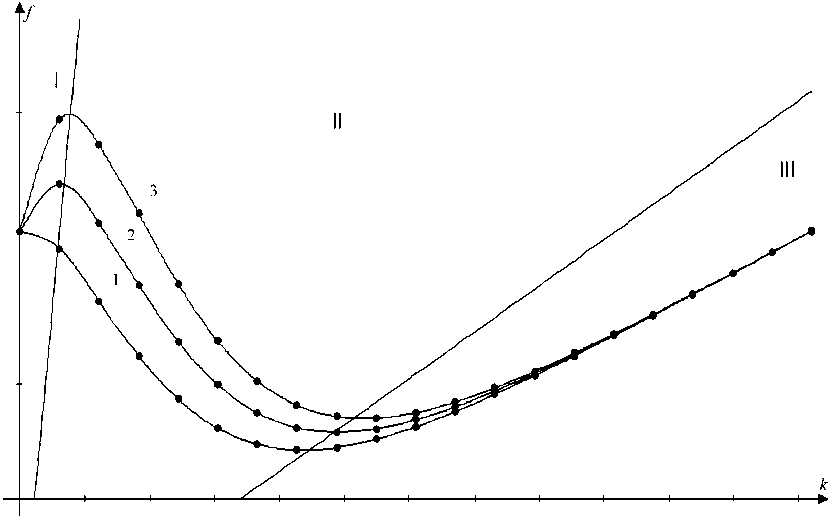
Рис. 5. Изменение коэффициента b при a, c, η, p, h –const

Fig. 5. Change of coefficient b at a, c, n, p, h - const свойства, как плотность, прочность, коэффициенты деформации, т.е. упругие характеристики трущихся тел, а также начальную степень шероховатости. Анализ размерностей указывает, что эта константа должна иметь величину обратной скорости (с/м). В настоящее время создаются модифицированные литейные сплавы с высоким сопротивлением износу, например, в работе [24] изучены коэффициент трения и износ заэвтектического по составу сплава алюминия с 15 wt.% кремния с супермодифицированной эвтектической структурой без первичных кристаллов кремния. Показано, что этот сплав с высокой прочностью и пластичностью имеет более низкий коэффициент трения и более высокое сопротивление износу, чем другие коммерческие сплавы.

Как было выяснено ранее, эмпирические константы а и b определяют коэффициент трения покоя и степень так называемого схватывания смазочного материала соответственно. И последняя постоянная c , находящаяся в показателе экспоненты, вероятнее всего, характеризует способность смазки адаптироваться к нагрузкам, так как с увеличением константы c положение минимума смещается в сторону начала координат, т.е. в более низкую область значений коэффициента трения и скорости сдвига (рис. 6). В работе [25] были показаны, что на каждом этапе роста нагрузки происходят изменения, выраженные на рис. 6. Это значит, что коэффициент c сильно зависит от погонной нагрузки и требует дальнейших теоретических и экспериментальных исследований. Окончательно уравнение (7) выглядит следующим образом:

f = (f_o+b^e-^cv+^- . (8)

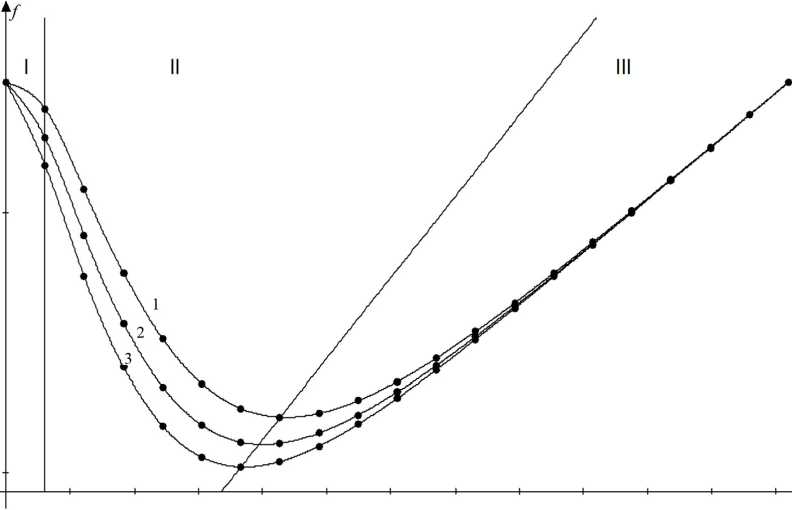
Рис. 6. Изменение коэффициента c при a, b, η, p, h – const

Fig. 6. Change of the coefficient c at a, b, n, p, h – const

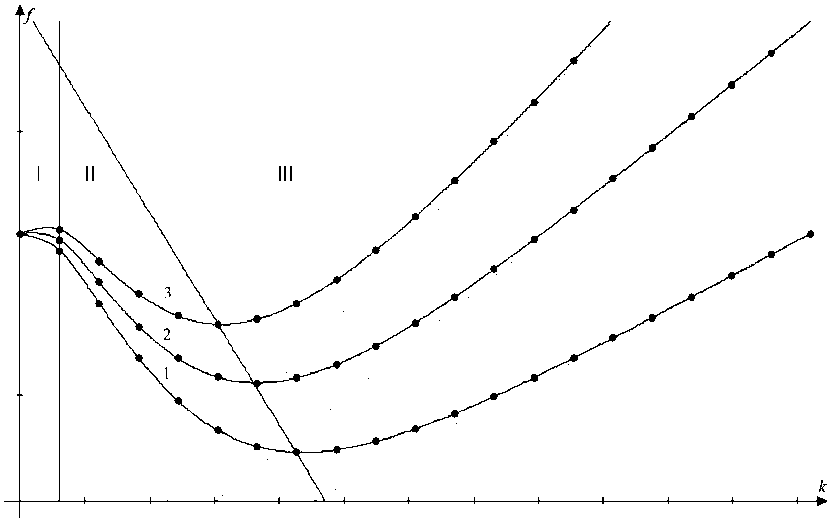
Рис. 7. Изменение коэффициента вязкости η при a, b, c, p, h – const

Fig. 7. Change in the viscosity coefficient η at a, b, c, p, h – const

Также было рассмотрено изменение вязкости смазочного материала во второй функций в уравнении (7). Как видно из графика (рис. 7), построенного при различных вязкостях, увеличение этого параметра приводит к тому, что в зоне жидкостного трения прямая приобретает более большой угол относительно оси скорости сдвига. Это утверждение подтверждается экс- – 845 –

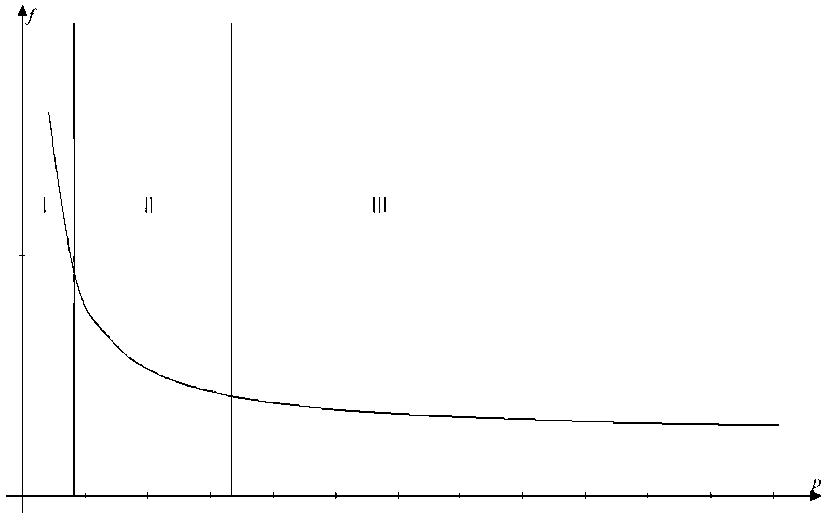
Рис. 8. График зависимости коэффициента трения от погонной нагрузки p при a, b, c, v, η, h – const

Fig. 8. Graph of the dependence of the coefficient of friction on the linear load p at a, b, c, v, n, h — const периментальными данными из работы [16]. Соответственно, если возрастание вязкости увеличивает угол наклона, значит, нарастание погонной нагрузки и толщины смазки обеспечивает меньший наклон прямой Петрова (на рис. 7 они изображены пунктирной линией).

В большинстве трибологических систем для изучения антифрикционных свойств смазочного материала целесообразным является исследование погонной нагрузки при фиксированном значении скорости скольжения. Изменение удельного давления в сторону увеличения или уменьшения даст возможность зафиксировать все возможные переходы режимов смазки от граничной до жидкостной. Для наглядности был построен график зависимости коэффициента трения от значения погонной нагрузки при фиксированной скорости скольжения (рис. 8). Экспериментальные данные из работы по исследованию режимов трения в подшипниках скольжения [6] указывают на то, что при низких значениях скорости сдвига должен наблюдаться характерный минимум, показывающий переход из смешанного трения в жидкостное. Следовательно, формула (8) представляет неполную картину изменения коэффициента трения, и требуется дальнейшее исследование.

Заключение

Очевидно, что коэффициент трения является характеристикой динамического процесса и зависит от материалов трущихся пар, конфигурации поверхностей, типов смазки и условий работы (свойства окружающей среды, скорости, нагрузки, температуры и т.д.). В связи с этим коэффициент трения представляет собой сложную функцию из нескольких переменных.

К сожалению, современная трибология не располагает аналитическими решениями, позволяющими вычислять коэффициенты трения в зависимости от заданных условий. Наиболее правильным было бы определение коэффициента трения любых пар путем измерения сил трения непосредственно на реальных объектах.

Основной результат данной работы выражен уравнением (8), которое представляет собой нелинейную полуэмпирическую формулу для расчета коэффициента трения. Это уравнение и отвечающие ему характерные графики представляют собой новую аналитическую зависимость для описания процесса трения трущихся пар и имеют следующие особенности:

• 1.    Точка 1 на графике, построенном с помощью формулы (8), является границей перехода из области граничного трения в область смешанного (см. рис. 1 и 4–8).

• 2.    Наличие неопределенных констант b и c , требующих теоретической интерпретации. Также не исключается возможность того, что они могут зависеть от динамических условий (скорости и погонной нагрузки).

• 3.    В данной формуле говорится о том, что вязкость является неизменяемой величиной, но в реальных условиях смазочный материал подвергается интенсивному воздействию, вследствие чего нельзя считать этот параметр постоянным.

• 4.    Под влияния большой нагрузки (скорости) возникает температурный градиент, который также влияет на множество факторов – вязкость и толщина смазочного слоя, упругость контактирующих тел, изменение шероховатости и пр.

Рассмотрение такой комплексной задачи, состоящей из нескольких варьируемых параметров, является очень сложным вопросом. В связи с этим была предпринята попытка получить аналитическую зависимость на основе аппроксимирующего выражения и формулы Петрова. Совершенно иной подход представлен в работе [27], характеризующий процесс контактного взаимодействия поверхностей (т.е. относительного перемещения) как химической реакции, которая описывается уравнением Аррениуса.