Исследования кольцевых литниковых систем

Время истечения жидкости из каждого питателя составляло 50-200 с в зависимости от количества одновременно работающих питателей, а вес вылившейся из питателя воды около 9 кг. Эти временные и весовые ограничения обеспечили отклонение от среднего значения скорости ±0,005 м/с, не более. Расход жидкости из каждого питателя определялся не менее 6 раз.

Рис. 1. Кольцевая литниковая система

Сначала рассчитаем истечение из питателя IV, когда гидравлическая цепь разомкнута в сечении 16–16 . Это L -образная ЛС. УБ для сечений 1–1 и 20–20 запишется так:

p 1          p 20      v 20

— + H =--+ О— + hi-20

^{Y         Y     2 g}       ,           (1)

где р 1 и р 20 - давления в сечениях 1-1 и 20-20 , Н/м² (равны атмосферному давлению: р 1 = р ₂₀ = Р а ); Y — удельный вес жидкого металла, Н/м³; а - коэффициент неравномерности распределения скорости по сечению потока (коэффициент

Кориолиса); принимаем а =1,1 [5]; g - ускорение свободного падения; g= 9,81 м/с²; v ₂₀ - скорость жидкости в сечении 20-20 , м/с; h _1-20 - потери напора при движении жидкости от сечения 1–1 до сечения 20-20 , м. Эти потери напора

, 2

h 1-20 =

l

Of Zem+X^

² g V       ^dem J

d

, 2

v

^{+ a} к~ ^{Z +}

² g I

^lem - IV d_к

+ 2Z + a v20 Zn + X b-2 g I

j

d

^

п J

,

где vem и v5 - скорости жидкости в стояке и в коллекторе в сечении 5-5, м/с; v5=v6=...v 10; Zem, ZK и Zn - коэффициенты местных сопротивлений входа металла из чаши в стояк, поворота из стояка в коллектор и поворота из коллектора в питатель; X - коэффициент потерь на трение; lem - длина (высота) стояка, м; lem-IV - расстояние от стояка до питателя IV, м; ln - длина питателя, м; dem, dK и dn - гидравлические диаметры стояка, коллектора и питателя, м; Z - коэффициент местного сопротивления поворота на 90º из сечения 5-5 в сечение 6-6 и из сечения 9-9 в сечение 10-10. Расход жидкости в системе

Q = v  S em = v 5 S = V 20 S .

Выразив скорости v_em и v ₅ через v ₂₀, получаем из (2)

(     1 к S к (     1 к 5 к 1

< 1 - 20(20) = Z em + X     Sk   + Z k + X “ + 2 Z      + Z n + X

V        d em К S em J V         d K        JV ^Sk J           d n

где Z i-2 ₀ ( ₂₀ ) - коэффициент сопротивления ЛС от сечения 1-1 до сечения 20-20 , приведённый к скорости v 20 в питателе IV. Коэффициент расхода системы от сечения 1-1 до сечения 20-20 , приведенный к скорости v 20

А 1 - 20(20)

^{( 1 + Z} 1- 20(20) У

.

Скорость

^V 20 = А - 20(20) к 2 gH / a

Для данной ЛС: d_em =0,02408 м, l_em =0,2675 м, d_K =0,01603 м, l_em-I =0,251 м, 1_ст-11=0,370 м, l_em- и т =0,489 м, l m V 0,742 м, d n =0,00903 м, l n =0,0495 м. Значения коэффициентов: X =0,03 [6], Z em =0,12 [7], Z K =0,396 [8], Z =0,885 [8], Z n =0,334 [8]. Результаты расчетов по выражениям (3)-(6) приведены в табл. 1.

Когда питатель IV находится в кольце, то УБ будет в виде (1). Однако течение идет по параллельным коллекторам 5-8-10 и 16-13-11, потери напора в них не суммируются, а берется одна из них. Так как v em = v 20 S n / S em , а v 5 = v 20 S n /2 S k , то (2) преобразуется к следующему виду:

(       1 к² а ² ( .       1 к 5 к 1

Z 1 - 20(20) = Z em + ^X "Г  7Г ⁺ZL5(5) + ^X + ² Z   хк  + Z n + ^X ~k

V         d em Jv S em J V             d K       JV ^{2 S} k J           d n

где Z 4 _-5 ( ₅ ) - коэффициент сопротивления на деление потока в сечении 4-4 между сечениями 5-5 и 16-16, отнесенный к скорости v ₅. Этот коэффициент подсчитываем по следующему соотношению из справочника [7]:

Zd = 1 + 1,5( vomd/v )2

⁽ v omd / v ^{) 2} , (8)

где v - скорость жидкости до деления потока, м/с; vomd - скорость жидкости в одном из каналов после деления потока, м/с. Чтобы найти Z4—5 (и равный ему ζд4-16), запишем очевидное равенство vemSem=2v5Sk=2v 16SK, из которого получается, что v5/vem=Sem/2SK=1,128278 - это и есть отношение vomd/v в формуле (8). Тогда по (8) находим, что Z4-5=Z4-16=2,285538. Результаты расчетов по соотношениям (7), (5), (6) и (3) - в табл. 1. Как видно, замыкание кольца привело к уменьшению коэффициента сопротивления Z1-2о<2о) с 0,865 до 0,644. Стало 2 потока жидкости, скорость в коллекторе упала в 2 раза, а потери напора в коллекторе на трение и в местных сопротивлениях уменьшились в 4 раза.

Таблица 1. Характеристики ЛС при работе одного питателя

Рабо таю щие пита-тели	Характеристики системы
	z	P	r / v 3Kc” , м/с	Q / Q эксп см 3 /с	Q o ", %
J **	0,684	0,771	1,961 1,932	125,59 123,75	+1,52
I	0,631	0,783	1,992 1,976	127,60 126,51	+0,86
II **	0,706	0,766	1,948 1,925	124,76 123,26	+1,22
II	0,634	0,782	1,991 1,995	127,48 125,19	+1,83
III **	0,729	0,761	1,935 1,904	123,95 121,97	+1,62
III	0,637	0,782	1,989 2,010	127,37 128,71	-1,04
IV **	0,865	0,732	1,863 1,822	119,31 116,66	+2,27
IV	0,644	0,780	1,984 2,024	127,07 129,63	-1,97

Примечание: * - Q 0 =(Q - Q^yQ”™; ** - гидравлическая система разомкнута в сечении 16–16

Характеристики работы только питателя III в разомкнутой в сечении 16-16 гидравлической системе находим по соотношениям (3)-(6), заменив в (4) l_cm-IV на l_cm-III , а 2 Z на Z ; см. табл. 1. Когда питатель III находится в кольце, то потери напора в параллельных трубопроводах 5-7-8 и 16-13-9 не суммируются и они равны друг другу. Поэтому давление р ₈ в сечении 8-8 равно давлению р ₉ в 9-9 , а перетекания жидкости из сечения 8-8 в сечение 9-9 или из 9-9 в 8-8 нет. УБ для сечений 4-4 и 19-19 (по пути через сечения 5-5 ,...8-8)

^Р 4 । a v cm

Y

2 g

__ f^д        । J lcm - III

= - 4-5(5) ^{+ Л}^-

V             d k

\

v

l

X

+    vL + z + Л ' + 1а vi + pa

2 g

V

d

п

2 g

Y

.

УБ для сечений 4-4 и 19-19 (через сечения 16-16 ,...9-9)

Р 4 +

Y

2 g

=   Z - 16(16)

V

.  ₁ lcm - III (16 - 9)

+ Л-------

d к

X

l

X

v

p

+ 3Z a + Z + Л ± + '  V9 + Ра

2 g

V

d

”     7

2 g

Y

.

Левые части выражений (9) и (10) равны. Приравниваем правые части и после преобразований получаем ( l_cm-III ( _16-9 ) =0,995 м):

v ₅

= ^v 16

Z -16(16) + 4,517134

Z -5(5) + 1,800159

Понятно, что Z _4-5 ( ₅ ) ^ Z 4-16(16) ; эти коэффициенты зависят - см. формулу (8) - от отношения скоростей v ₅/ v_cm и v ₁₆/ v_cm , которые неизвестны. Предположим, что v₅ =1,1 v ₁₆. Тогда v_cmS_cm = = ( v ₅+ v ₁₆) S_k = (1,1 v 16 + v 16 ) S k =2,1 v 16 S k . Отсюда v 6 v cm = S cm /2,1 S k . По (8) находим: Z _4-16 ( ₁₆ ) -2,366058. Так как v 5 =1,1 v 16 , то V 16 =0,909091 v 5 . v cm S cm = ( v 5 + v 16 ) S k =( v 5 +0,090901 v 5 ) S k = 1,909091 V 5 S к . И v 5 / v cm = S cm / 1,909091S к =1,182005. По (8) определяем:

Z _4-5 ( ₅ ) =2,215750. Подставляем найденные значения Z 4-5(5) и Z 4-16(16) в (11) и получаем: v 5 =1,309191 v ₁₆. А мы задавались v ₅=1,1 v ₁₆. Делаем следующее приближение - v ₅=1,309191 v ₁₆ - и повторяем расчёт. После ряда приближений при заданном v ₅=1,350291 v ₁₆ получаем по расчёту v 5 =1,3502911 v ₁₆. Расчёт этого отношения можно закончить, так как разница между заданным и рассчитанным значениями v ₅/ v ₁₆ составляет всего 0,0000001. При этом у 4-5(5) =2,094972, £ 4-16(16) =2,584805, а v 16 =0,740581 v 5 , v cm = v 19 S „ / S cm , ( v 5 + v 16 ) S k =( v 5 +0,740581 v 5 ) S k =1,740581 v 5 S k = v 19 S n .

Или v ₅= v 19 S n /1,740581 S_k . Коэффициент сопротивления ЛС от сечения 1-1 до сечения 19-19 , приведённый к скорости v ₁₉ в питателе III [(см. зависимости (2), (7) и (9)]

^Z 1 - 19(19) =

V

ir z +2 -lcm-cm , dcm 7V

S п

S cm 7

+ е д - 5<5)

V

+ Л ¹ c-m - III

dк

+ z

7V

S п

1,740581 S _K 7

+ z + Л lj a п

.

Результаты расчетов по (12), (5), (6) и (3) приведены в табл. 1. Как видно, замыкание кольца привело к уменьшению коэффициента сопротивления ζ 1-19(19) с 0,729 до 0,637. Появление параллельного коллектора привело к падению скоростей в каждой из линий, к снижению потерь на трение и в местных сопротивлениях, что и вызвало уменьшение ζ 1-19(19) , рост μ 1-19(19) , v 19 и Q 19 по сравнению со случаем, когда питатель III работал при разрыве кольца в сечении 16–16 .

Когда в гидравлически замкнутой ЛС работают питатели II и III (см. рис. 1), в питатель III поступает жидкость из сечений 8–8 и 9–9, а в питатель II – только из сечения 7–7, да и то не вся. В рассматриваемом кольце имеются два разных потока: один против часовой стрелки (16–13–9), другой – по часовой стрелке (5–6–7– 8). Движение жидкости в сечении 8–8 – справа налево. В данном случае при работе двух питателей это определяется легко. Потоки встречаются на входе в питатель III в точке A (рис. 2), которая называется точкой водораздела или ну- левой точкой [5, с. 216-217]. Мысленно разрезаем наше кольцо по намеченной линии водораздела и получаем сеть, изображенную на рис. 2. Далее по обычным формулам подсчитываем потери напора для линии 1–16–13–9–19' h1-16-9-19′ и для линии 1–5–8–19'' h1-5-8-19′′. После этого сопоставляем между собой две найденные потери напора. Если h1-16-9-19′=h1-16-9-19′′, то заключаем, что напоры в точках A′ и A′′ будут одинаковыми, что и должно быть, поскольку точки A′ и A′′ представляют собой физически одна точку A. Следовательно, получив указанное равенство, можем утверждать, что мы правильно задались величинами расходов Q7, Q8 и Q9. Если указанное равенство не получается, то приходится изменять величины этих расходов, а иногда и переносить точку водораздела, например, в точку B – в точку входа жидкости в питатель II (см. рис. 2). При этом обращаемся ко 2-й, 3-й и последующим попыткам, добиваясь того, чтобы приведенное выше равенство было выдержано с нужной точностью. Составим УБ для сечений 1–1 и 18–18 (для пути через сечения 2–2,… 5–5,… 7–7)

Я । p a            ; lcm ~ ^Vc— । дд       , 1 l c— - II

+-- = Zc— + ^с- а ст- + Z4-5(5) + X , y          d 2g I          d

•                   cm 7 g                      к

+Z'7

v ²

а — +

2 g

Z18 + X ^ + 11а V + p, I      dn   7  2 g Y

и для сечений 1–1 и 19–19 (для пути через сечения 2–2 ,… 16–16 ,… 13–13 ,… 9–9 )

l

h+p" = Zc— + Xl—

\

Y

к

d , ст

а

v

vст       д

+ ^Z 4-16(16)

2 g

к

_|_ ^ lc— - III (16-9) _|_

d

к

где ζ 18 – коэффициент сопротивления на ответвление части потока из сечения 7–7 коллектора в питатель II с выходным сечением 18–18 . Потребуется также подсчитывать ζ 8 – коэффициент сопротивления на проход жидкости из сечения 7–7 в сечение 8–8 при ответвлении части потока из сечения 7–7 в питатель II. ζ 18 находим по соотношению [9, с. 112-115]

Zo—B =[1 + t(Vn I vK У ]/(Vn I vk У

,

\

а ζ 8 – по следующей зависимости

Zn= 0,4(1 - Vnp 1VK ^/(vnp 1VK )

,

\

3Z а V1A + Z + Xm + 1а V^ + Ра

2 g

к

l

v

p

d

п

2 g

^Y ,(14)

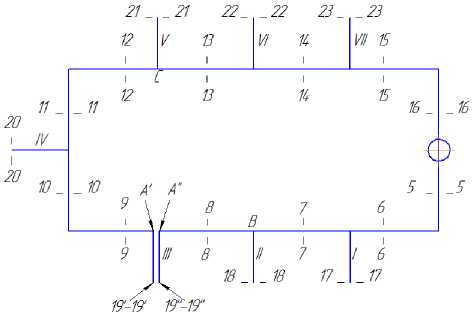
Рис. 2. Схема для расчета при работе питателей II и III

где v к и v пр – скорости металла в коллекторе до и после ответвления части потока в питатель, м/с; v n – скорость жидкости в питателе, м/с; τ – коэффициент. Для нашего случая при S n / S к =0,317 τ =0,15. Коэффициент ζ пр получается приведенным к скорости проходящего потока v пр , а ζ отв – к скорости в питателе v n .

Запишем очевидные равенства:

Q = Q c— = V c— S c— = Q 5 + Q 16 = V 5 S k + V 16 S к =

= Q 18 + Q 19 = V 18 S n + V 19 S n

Q 8 = V 8 S k = Q 7 - Q_X 8 = V 7 S k - V ₁₈ S n , Q 19 = V 1 S n = Q 8 + Q₉ = V 8 S k + V 9 S k

Как видно, у нас 3 уравнения - (13), (14), (17) - и 6 неизвестных величин скоростей v_cm , v ₅, v ₈, v ₁₆, v is , v 19 и двух коэффициентов Z 8 и Z 18 , зависящих от отношений v ₈/ v ₇ и v ₁₈/ v ₇, которые тоже неизвестны, см. формулы (15) и (16). Казалось бы, задача не поддается решению. Поступим таким образом. Введём следующие обозначения: v 18/19 = v 18 / v 19 , X = v 8 / v 7 , У = v 5 / v 16 . А Q 8 = xQ 7 , v 7 = v 8 / X , Q 16 = Q 5 / У , v 16 = v 5 / у , v 5 = v 6 = v 7 , v 9 = v 10=.. = v 15 = v 16 .

Расход жидкости в системе

^Q = ⁽ v 18 + v 19 ) ^Sn = ⁽ v 18/19 v 19 + v 19 ) ^Sn =

= v 19 ^{( V} 18/19 + 1 ) ^Sn = v 19 ^Snp (19)

^где S np (19) = ^{( 1} + v 18/19 ) ^Sn - приведенная к скорости v ₁₉ - площадь питателей (учитывает работу обоих питателей). А v_cm = v ₁₉ S_np ( ₁₉ ) / S_cm. Аналогично записываем:

Q = ⁽ V 1₈ + ^v 19 ) 5_Я

v„ +

V        ^v 18/19 )

S,

= V18 1 +

-1-

^V 18/19 )

^Sn = ^V 18 ^Snp (18)

где S np (18) =[ 1 ⁺     I S n - приведенная (к скорости v ₁₈) площадь питателей. И v_cm = v ₁₈ S_np ( ₁₈ ) / S_cm . Име-

V      ^v 18/19 )

ем также:

^Q   v cm ^Scm

= (v5 + v16 ) Sk =

v

^V 5 ⁺ T ^S

V    y)

к

= v 5

V

1 + 1 1 S y )

к

v ₅

У S cm =_v У ^Snp (18) 1 + yS k    ¹⁸1 + y S k

Теперь выражение (13) можно записать так:

H = a v8

r

² g V

£ + 2 -l^- cm d u cm )

S cm )

+ Zt5(5) V

+ ^ / ст - т/.

d

к

+z

yS пр (18)

(1 + У ) S к )

^{+ Z} 18 ^{+ 2} , ^{+ 1}

d п

Выражение в квадратных скобках (за исключением “1”) - это коэффициент сопротивления системы от сечения 1-1 до сечения 18-18 Z 1- ₁₈ ( ₁₈ ) . Принимаем (произвольно): x = v ₈/ v ₇=0,4, У = v 5 / v 16 =1,6, v 18/19 =1. При x =0,4 Z 8 =0,9, а Z 18 =0,429714, см. формулы (15) и (16). Для у =16 по (8) находим, что Z _4-5 ( ₅ ) =2,018579, а Z _4-16 ( ₁₆ ) =2,827562. Результаты расчетов: Z i-18(18) =1,178541, ц 1-18(18) =0,677512, v 18 =1,723946 м/с, Q 18 =110,405056 10^-6 м³/с.

Для питателя III (линия ^-16-19 ) действительны следующие соотношения:

^Q = v cm S cm = ⁽ v 5 ⁺ v 16 ) ^Sk = ⁽ yv 16 ⁺ v 16 ) ^Sk = v 16 ⁽ У ⁺ 1 ) ^Sk

V , = Vo = V 16     9      ст

1   S ст

1 + У S k

= ^V 19

1 ^Sпр (19)

1 + У S k

И выражение (14) будет выглядеть так:

H = a v ⁹

² g V

Z cm + ² lir a ст

" S np (H9)

V S cm

12    <   .

I +   Z 4 ^g -16(16) + 2

V

l cm - III (16-9) d к

S ^{np (19)}   1 + Z + 2 l^- + 1

(1 + у ) S к )    ⁿ"      d n

J . (19)

Выражение в квадратных скобках (за исключением “1”) - это коэффициент сопротивления системы от сечения 1-1 до сечения 19-19 (для линии 1-16-9) Z1-19(19). Подсчитываем: Z1-19(19) = =0,971933, ц 1-19(19)=0,712121, v19=1,812009 м/с, Q19=116,044835 10-6 м3/с. Расход в системе Q=Q18+Q19=222,582933 10-6 м3/с. vст=QIScm = +0,488753 м/с. Q5=Qy/(1+у)=136,974112 10-6 м3/с, v5=Q5/Sk=0,678706 м/с. Q16=Q/(1+у)=85,608820 10-^ м3/с, v 16=Q16/Scm=0,424191 м/с. Значения отношений x=0,4, y=1,6 и v18/19=1 были взяты произвольно. Предположим, что в результате расчётов у =1,6 и v 18/19=1 не изменились. Найдем x. Расход Q8=Q5 - Q18=26,569057 10-6 м3/с, а скорость v 8=Q 8/Sk=0,131649 м/с. Отношение x=v8/v7=v8/v5=0,193971. А мы задавались x=0,4.

В системе должно быть следующее равенство: p ₉= p ₈ Проверим это соотношение. Составим УБ для сечений 1-1 и 8-8 :

H + pi =

Y

/

V

л    bm_\a vcm +

^Z ст     7 ^a ^

ст      g

-

V

+ xl cm z I L d к

+ Z l a — + J 2 g

Z + X — + 1 1 a ' 82 + p

V ⁸     d k   J 2 g Y

где l – расстояние между питателями II и III; l =0,119 м. Заметим, что p 8 ≠ p a . Запишем (20) так:

H = ^{P 8 P a} = H —

Y

/

V

Cm + X-l^ la d l 2g ст     g

—

гд + x lcm—II       — z4—5(5) + X d + z Ja 2g

—

/

V

l      ¹    - 2

Z y + X + 1 1 a .

^{8    2} d k )  ² g (21)

Подсчитаем по формуле (16) ζ 8 для отношения x =0,193971: ζ 8 =6,906939. Все величины в (21) известны. Находим, что H 8 =0,256159 м. Составим УБ для сечений 1–1 и 9–9 (линия 1–16–9 ):

2                           —1П.,2

H + p" = Zcm + Xl^^ av^m + Zd—I6(i6) + XCm——111 (16—9)----- + 3Z + 1a+

Y V       dcm )  2 g V                dk              J 2 g Y p9≠pa. Выражение (22) запишется следующим образом:

Tj _ P 9 pa   IJ         । 1 lcm  vTcm     дд         -j cm——UI(16—9)   C2 д i

H 9 =------= H ^{— z} cm ⁺ ^ T" a,— ^z 4 — 16(16) ^{+ X} -----------⁺ 3 ^{Z +1 a} ■;;-.

Y         V       dcm J  2 g  V                 dk              J

Определяем по (23): H 9 =0,272746 м. Напор H 9 в сечении 9–9 больше напора H 8 в сечении 8–8 на 0,016587м. В данной ЛС с одним стояком и двумя работающими питателями это невозможно. Поэтому задаемся следующими величинами: x = v 8 / v 7 =0,193971, y = v 5 / v 16 =1,6 и v 18 / v 19 =1. Получаем: H 9 – H 8 =0,017906 м, x =0,180700, v 18 /v 19 =0,116880.

Действуя таким образом, получаем, что при x =0,1391059, y =1,43712931 и v 18 / v 19 =1/03108789. H 9 – H 8 =–2,2, 10^-9 м. При этом по расчету x =0,13910596, а v 18 / v 19 = =1,03108791. По-видимому, разность H 9 – H 8 можно привести к любой наперед заданной бесконечно малой величине, хотя в системе неизвестных больше, чем уравнений. Понятно, что разность напоров в 10^–9 м бессмысленна. Нужно было убедиться в работоспособности предлагаемой методики расчета.

Поступая аналогичным образом, находим характеристики ЛС при разном количестве работающих питателей (табл. 2). Как следует из табл. 1 и 2, отличие опытных данных от расчетных невелико (maх 2,5% по расходу в ЛС и max 5,5% по расходу в питателе) и даже ставит под сомнение результаты работы. Хотя это отмечалось и при исследовании ЛС, перечисленных в начале статьи. Но ошибок ни в расчетах, ни в постановке экспериментов, ни в обработке опытных данных найдено не было. Даже на такой сложной ЛС как кольцевая, УБ не дает каких-либо сбоев и вполне согласуется с опытными данными. По-видимому, УБ можно использовать при расчетах систем с переменным расходом (массой). По крайней мере, для ЛС это доказано экспериментально. Впечатляет ЛС из питателей I–III, когда по линии 16–13–9 нет раздачи потока, и он целиком подходит к питателям III и II, а точка водораздела находится в B (см. рис. 2).

Как видно, по предлагаемой схеме можно решать систему, когда число неизвестных превышает число уравнений. Вначале произвольно задаемся множеством неизвестных величин, вроде бы не связанных друг с другом (для питателей I–III это v 17 / v 18 , v 18 / v 19 , v 5 / v 16 , v 7 / v 6 , v 8 / v 9 ). И получение заданной величины разности H 8 – H 7 при подборе перечисленных величин ведет к решению системы уравнений, описывающих работу данной ЛС. То есть УБ «перемалывает» все таким образом, что разность давлений справа и слева около нулевой точки стремится к нулю только при определенных значениях других величин. Попытки сделать его равным 0 только за счет какого-то одного фактора предпринимались, однако остальные факторы – заданные в начале и получившиеся в результате расчета – становились неприемлемо разными. Нужно менять все влияющие на работу ЛС факторы. А экспериментально процесс истечения жидкости устанавливается очень быстро, за 3-5 с, даже при резком «перекосе» в системе, когда работают, например, питатели I–III и VII. Питатели «знают» свою скорость истечения жидкости. По-видимому, происходит нечто такое, что ещё предстоит понять. Здесь потребовалось рассчитывать приведенные площади для всех питателей, например, S пр(17) , S пр(18) и S пр(19) при работе питателей I–III. В исследованных ранее ЛС можно было находить приведенную площадь питателей только для скорости в жидкости в одном из питателей.

Таблица 2. Характеристики ЛС при работе нескольких питателей

Работающие питатели	Характеристики системы
	ζ 1-19(19)	μ 1-19(19)	v 19 эксп v 19 , м/с	v 18 эксп v 18 , м/с	v 17 эксп v 17 , м/с	Q 19 эксп Q 19 , см 3 /с	Q эксп , см 3 /с	Q 0 , %
II, III*	1,530	0,629	1,600 1,626	1,514 1,547		102,46 104,13	199,36 203,21	–1,89
II,III	1,105	0,689	1,754 1,770	1,808 1,752		112,32 113,35	228,13 225,56	+1,14
I, III*	2,470	0,537	1,366 1,374	1,292 1,319	1,128 1,166	87,48 87,99	242,42 247,10	–1,89
I, III	1,639	0,616	1,566 1,525	1,556 1,558	1,514 1,455	100,30 97,66	296,92 290,62	+2,17
I, III, VII**	2,365	0,545	1,387 1,390	1,432 1,362	1,301 1,207	88,83 88,99	358,08 349,29	+2,52
I, III, V, VI***	3,031	0,498	1,267 1,256	1,259 1,209	1,119 1,098	81,16 80,42	390,23 384,96	+1,35
I VII****	4,775	0,416	1,059 1,004	0,945 0,954	0,811 0,830	67,81 64,31	427,68 422,62	+1,20

Примечание: * - гидравлическая система разомкнута в сечении 16–16 ; ** - v ₂₃=1,471 м/с, v ₂₃ ^эксп =1,433 м/с; *** - v 21 =1,291 м/с, v 21 ^эксп =1,277 м/с, v 22 =1,157 м/с, v 22 ^эксп =1,171 м/с; **** - ζ 1-20(20) =4,904; μ 1-20(20) =0,412, v 20 =1,047 м/с, v 20 ^эксп = 1,024 м/с

Выводы: впервые теоретически и экспериментально исследована кольцевая литниковая система. Получено хорошее соответствие рас-  ^5.

четных и опытных данных. Для теоретического исследования таких систем создана и зарегист- . рирована в государственном реестре программа для ЭВМ [10].