Исследования колебательных процессов в несущем канате лесотранспортной системы на базе плавающих воздухо-опорных конструкций

Введение. Канатная лесотранспортная система на базе плавающих воздухоопорных конструкций предназначена для обеспечения временной оперативной переброски заготовленной древесины и другого груза с необорудованных береговых территорий на водные транспортные средства без использования кранового и причального оборудования, а также при невозможности использования шпангоутов из-за рифов или высокого берега. Транспортировка древесины осуществляется в подвесном режиме с помощью самоходной радиоуправляемой каретки, передвигающейся по несущему канату, который удерживается с помощью воздухоопорных плавающих конструкций, особенностью которых является наличие внутренних шаровых и торовых элементов, служащих демпфером и обеспечивающих одновременно жесткость и гибкость конструкции, а также одновременно устойчивость конструкции на водной поверхности [1, 2]. Общий вид лесотранспортной системы представлен на рисунке 1.

Рис. 1. Канатная лесотранспортная система на базе воздухоопорных плавающих конструкций

Проведенные экспериментальные исследования на мини-моделях выявили наличие в несущем канате сложных колебательных процессов, возникающих как в момент перемещения грузовой каретки, так и во время воздействия волновой и ветровой нагрузок. Данный процесс колебаний приводит к увеличению провиса несущего каната и, как следствие, к уменьшению скорости перемещения каретки.

Цель исследований. Изучить процесс развития продольных и поперечных колебаний, возникающих в несущем канате при перемещении грузовой каретки и воздействии волновой и ветровой нагрузок.

Рассматриваемая задача во многом специфична: в отличие от канатных трелевочных систем, расположенных на земле, плавающие опоры нельзя считать неподвижными, при этом необходимо рассмотреть колебания канатной дороги, состоящей из нескольких секций, то есть число опор больше двух. Таким образом, даже с учетом возможности замены (идеализации) опор на сосредоточенные массы в системе будет присутствовать несколько подвижных масс, перемещения которых связаны растяжимой нитью (рис. 2). Необходимо отметить, что несущий канат способен оказывать сопротивление только растяжению. По этой причине можно говорить о физической нелинейности исследуемой системы.

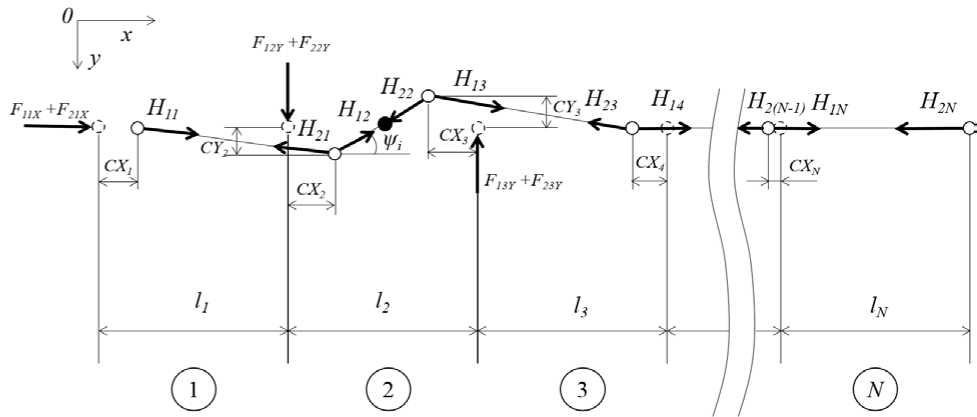
Рис.2. Основная расчетная схема для определения подвижности системы

Для реализации математической модели, описывающей колебания всей канатной системы, использовались методы аппроксимации данных, полученных из численных решений дифференциальных уравнений движения системы.

Действие ветровой и волновой нагрузки будем учитывать с помощью значений эквивалентных усилий F 1 , F 2 , приложенных к вершинам мачт воздухоопорных конструкций либо по оси x , либо по оси y (рис. 3).

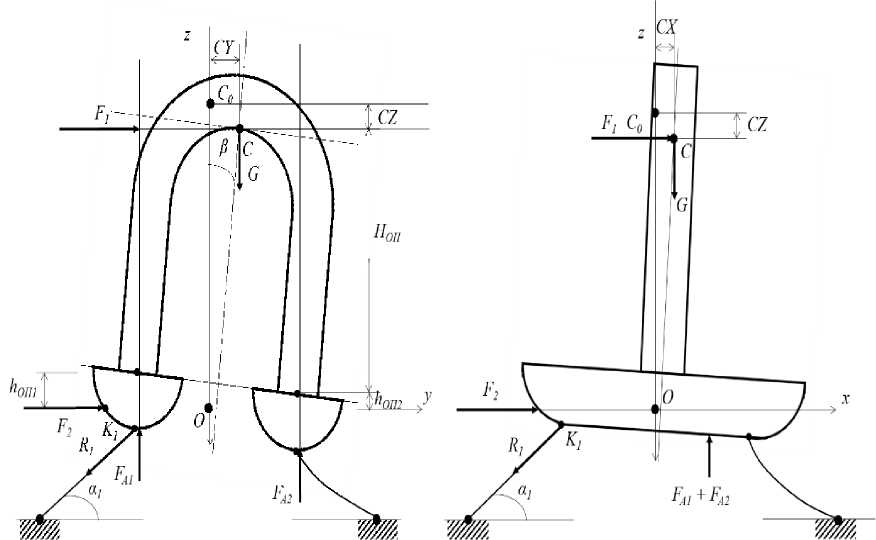
Рис.3. Расчетная схема при воздействии на систему ветра, волн и груза

Процесс развития продольных колебаний плавучих опор описывается системой дифференциальных уравнений второго порядка, которые в общем виде задаются следующим образом:

m^ddX ^{+ Г}^ ⁺ K»' ^CX i = f ⁽ CX ⁾⁺ f ^(Ш)+ f ⁽ FX * ,

где    CX i – перемещение вершины мачты по оси x ;

• m i – масса опоры;

• γ i – коэффициент демпфирования;

K Xi – аналог коэффициента жесткости, связывающий сопротивление перемещению вершин опор по оси x и усилия, им противодействующие (обусловлены действием якорей и сил Архимеда при отклонении оси опоры от вертикали)

K

Xi

^A Xi ^F 1 iX + ^B Xi ’ F 2 iX

A*= 279

H

0,811 ОП

R 0,796 LX 1,777

^BXi    ²⁶ R 0 , 796 LX 0 , 1431 ;

f ( CX ) – функция, характеризующая влияние усилия со стороны растянутого несущего каната за счет смещения вершин опор друг относительно друга

.f ( CX ) = C i HeCX + - CX,) - C i - i He ( CX i - CX-, ) ;         (3)

He( ξ ) – единичная функция Хевисайда, определяемая формулой

He ( ^ ) =

0 ^ <  0

1 Л >  0 ’

С i – усилие сопротивления растяжению троса при смещении вершин опор друг относительно друга

EA ,

C i= — - ( CX _l+i - CX i) ;

li

f(FX) – функция, характеризующая влияние ветровой и волновой нагрузки на колебания опоры f (FX ) = F1X + F^;

F 1i , F 2i – усилия, эквивалентные ветровой и волновой нагрузкам на i- ю опору по оси x соответственно

F ii = Fwbbetp = 0 , 00052 d 0“ H О“⁷ v^{1 , 979} ;                           (7)

R 1 , 396 h

^F 2i = F экввoлнx = ¹⁹ , 094 • lx ₀ , 6₀₄ ^ ^;                             (8)

f(H) – функция, характеризующая воздействие на опору за счет перемещения каретки с грузом (передается со стороны растянутого несущего каната)

.f ( HX ) = H i, H [ 'V - t

• He t

-

^{( i -} 1 ) ' l '

\

-

\

V J

H      ^{f (} i - 1 ) • l i

- H He I------

²      \ V

-

t

• He i t

-

( ' - 2 ) - 1 ' Y

V

;

i – индекс, соответствующий номеру опоры (отсчет ведется от самой удаленной от берега опоры, нумерация начинается с единицы).

Процесс развития поперечных колебаний плавучих опор (вершин их мачт) также описывается системой дифференциальных уравнений второго порядка, уравнения в общем виде задаются следующим образом:

d 2 CY    dCY mi -г- + Yi-nf + Kri • CYi = f (CY)+f (FY);                  (10)

dt2 dt где   CYi – перемещение вершины мачты по оси y;

K Yi – аналог коэффициента жесткости, связывающий сопротивление перемещению вершин опор по оси y и усилия, им противодействующие (обусловлены действием якорей и сил Архимеда при отклонении оси опоры от вертикали)

,

Yi¹ 1 iY + ^Yi ¹ 2 iY

H 0,894

A.. = 127 ————---—. в = 9 53-------1•

Yi                0,796      0,94       1,764 Yi ,         0,796      0,8010

iii    iii

f(CY) – функция, характеризующая влияние усилия со стороны растянутого несущего каната за счет смещения вершин опор друг относительно друга f (CY) = CY He(CYi+1 - CYi) - C(i-„ y He(CY - CYi -);(12)

СiY – усилие сопротивления растяжению троса при смещении вершин опор друг относительно друга введение множителя

CYi = , '(CY' i+1)Y li

- cy )-

[ ■> - Ci . i

I         l i

\

( CY + CY ,1

,        ‘ ^{+ 1}

к        ^li       7

в формулу (13) обусловлено необходимостью учесть влияние угла

ψ i (схема на рис. 2) на составляющие натяжения несущего каната по оси y при поперечных колебаниях вершин плавучих опор;

f(FX) – функция, характеризующая влияние ветровой и волновой нагрузки на колебания опоры f (FY )= F„ + F^.

F =F „  =9,547-

2 iY ЭКВВОЛНY ,->^^f    ^

(значение F 1iY определяется по формуле (7)).

Аналитическое решение систем уравнений вида (1), (10) невозможно, вследствие чего прибегнем к численным методам решения с последующей аппроксимацией расчетных данных при помощи метода наименьших квадратов по [3–5]. Для этого зададимся исходными данными в диапазоне, представленном в таблице.

Исходные данные к численному решению системы уравнений (1), (10)

Параметр	Размерность	Минимальное значение	Максимальное значение	Шаг изменения при расчете
l	м	25	100	25
G	кН	5	45	10
V	м/с	2	8	2
H ОП	м	10	15	2,5
LX	м	5	7	1
LY	м	5	7	1
F 1	кН	0	100	20
F 2	кН	0	100	20
N	-	2	6	1
α	0	0	45	15

Проведенные расчеты показали, что во всех случаях максимальная амплитуда продольных колебаний отмечается при прохождении кареткой с грузом точки, соответствующей середине пролета (рис. 4).

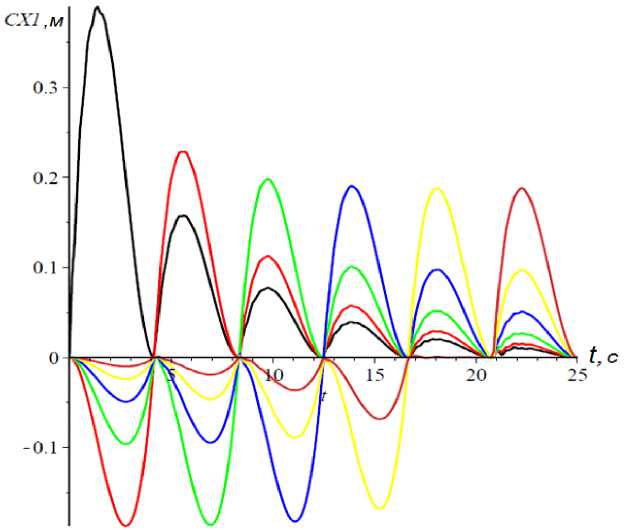
Рис. 4. Пример распространения продольных колебаний в канатной лесотранспортной системе при l=25 м, G=35 кН, V=2 м/с

При этом характер взаимных смещений вершин мачт, которые определяют удлинения (либо укорочения) секций канатной системы, также сохраняется. Обозначим эти изменения длины символом Δ

Д, = CXi - CXi-1,

где индекс i соответствует номеру секции (отсчет ведется с единицы, наиболее удаленной от берега опоры).

Поскольку анализ численных результатов решения системы дифференциальных уравнений вида (1) показал, что представленная на графиках картина развития продольных колебаний вершин мачт плавучих опор сохраняется при варьировании исходных данных для расчетов в диапазоне, представленном в таблице, результаты расчетов (максимальное сближение вершин мачт) можно аппроксимировать следующей зависимостью:

^Д iMAX

0 , 0265 • V^{1, 326} ( G + 1 ) ^{0 , 533} ( F + F ₂ + 1 ) ^{0 , 817} 1^{0, 262} -------------/ ----- ²--- 4------ cos a .

LX^{1 , 198} exp ( - 0 , 119 • [ N - n + 1 ])

Если рассматривать провис каната в месте нахождения каретки с грузом как суперпозицию двух перемещений (одно из них вызвано уменьшением длины секции дороги при сближении вершин опор, второе обусловлено действием динамического усилия со стороны каретки), тогда дополнительную величину вертикального перемещения каретки определим через величину сближения вершин мачт следующим образом:

z MAX, ДОП

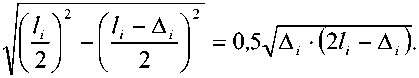
Выражения (1), (17), (18) в сумме позволяют оценить максимальное значение провиса каната при перемещении каретки с грузом с учетом как вертикальных колебаний каретки, так и продольных колебаний вершин плавучих опор.

Графики на рисунке 5 отражают влияние скорости V на величину сближения вершин мачт по сравнению с влиянием G и, как следствие, увеличение значений провиса несущего каната.

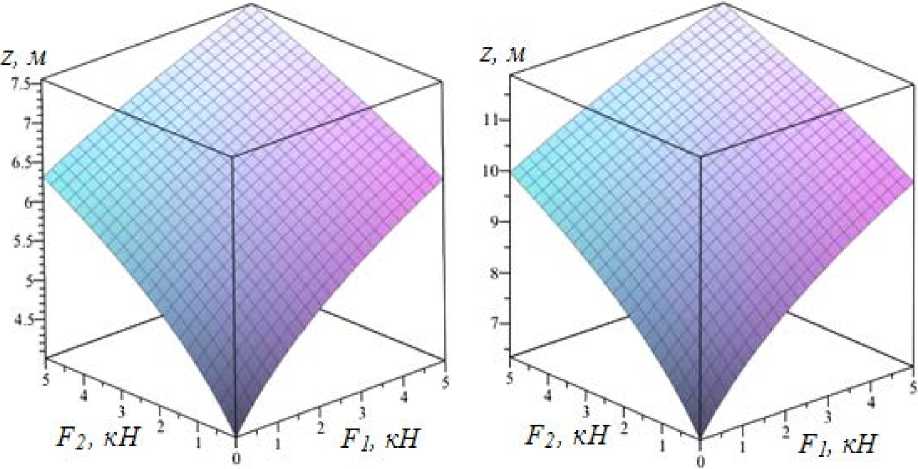
а) V=2м/с, G=30кН              б) V=4м/с, G=30кН

Рис. 5. Зависимость провиса несущего каната от скорости движения каретки и влияния внешних факторов (F 1 , F 2 – эквиваленты ветровой и волновой нагрузок)

Сформулируем технологическую рекомендацию по определению допустимой скорости каретки с грузом исходя из ограничения по максимальному провису каната. Зададимся допустимой величиной провиса каната [ z ] в 10 % от длины пролета l , тогда система уравнений, ограничивающих скорость V и вес G каретки, примет вид

A iMAX

Zmax = 0,0223 • L- ³

G • V ² • cos ⁴ a

EA

0,0265 • V ¹³²⁶ ( G + 1 ) ^0,53 3 ( F + F 2 + 1 ) ^0,81 7 1 ⁰-²⁶² LX ¹⁴⁹⁸ exp ( - 0,119 • [ N - n + 1 ] )       c

z MAX , ДОП 0,5^/ ^A i '{2 ^[ z ^] = z MAX + z MAX , ДОП

l. -A )

l             I /

= 0,1 l i

Расчеты при варьировании угла наклона несущего каната по отношению к горизонту показали, что практически при всех вариантах задания исходных данных зависимость снижения суммарной величины максимального провиса каната (в процентах по отношению к случаю α = 0⁰) по мере увеличения данного угла описывается графиком на рисунке 6.

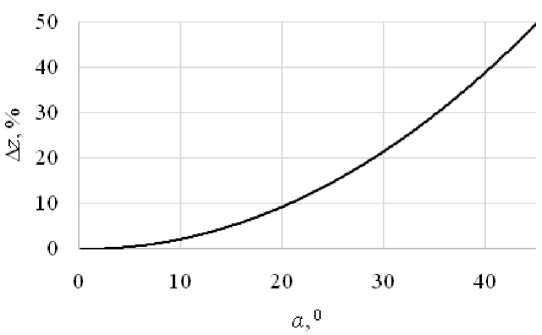
Рис.6. Снижение максимальной величины провиса z несущего каната по мере увеличения его угла наклона α по отношению к горизонту

Выводы

• 1.    Установлено, что скорость перемещения каретки оказывает более существенное влияние на колебания системы и провис несущего каната, чем масса перемещаемого груза, ветровая и волновая нагрузки.

• 2.    Теоретически установленный факт снижения провиса каната за счет проектирования дороги с наклоном несущего каната дает основание говорить о дополнительном резерве повышения эксплуатационных качеств, предлагаемого технического решения для трелевки древесины.

• 3.    Поперечные колебания мачт канатной дороги заметно меньше по величине, чем продольные. Это объясняется тем, что динамические усилия со стороны движущейся каретки действуют в плоскости ZOX (в которой развиваются продольные колебания), поперечные колебания в рамках принятой модели развиваются в плоскости XOY . Таким образом, можно заключить, что при эксплуатации канатной дороги в разрешенном диапазоне скорости ветра поперечные колебания не могут нарушить ее работу в том случае, если нормальная работа установки обеспечена с точки зрения продольных колебаний мачт.

• 2.

• 3.

• 4.

• 5.