Исследования конденсированных сред с использованием времяпролетного спектрометра очень холодных нейтронов

Макроскопические свойства материалов, такие как электропроводность, теплопроводность, прочность, радиационная стойкость и морозостойкость, во многом обуславливаются структурами с характерными размерами от единиц до сотен нанометров (наноструктур). В этом диапазоне находятся размеры неоднородностей различной физической природы в кристаллизующихся полимерах [1], размеры мицелл в лиотропных жидких кристаллах [2], размеры доменов в блок-сополимерах [3] и функциональных элементов биологических объектов [4]. В этом же диапазоне, по-видимому, находится предел возможной миниатюризации электроники [5]. Этот далеко не полный перечень дает краткое представление об актуальности исследований наноструктур. Особенно важно их изучение с целью создания новых материалов для различных наукоемких технологий.

Очень холодные нейтроны (ОХН) рассеиваются и поглощаются ядрами атомов. Сечения поглощения таких нейтронов существенно ниже, чем рентгеновских лучей. Это дает возможность успешно проводить исследования нано структур массивных образцов. Наличие у нейтрона магнитного момента позволяет исследовать распределение спиновой плотности в этих образцах. С целью использования свойств ОХН для проведения исследований новых материалов в нейтронно-физическом отделе ФИАН группой сотрудников Нейтронно-физического отдела под руководством Ю.А. Мерку-льева создан и установлен на реакторе ИРТ МИФИ времяпролетный спектрометр ОХН [6].

Метод рассеяния очень холодных нейтронов

Энергия очень холодных нейтронов 2,5 • 10 ^{- 7} <  E <  5 • 10 ^{- 5} эВ много меньше энергии химических связей, существующих между атомами, поэтому рассеяние ОХН на неоднородностях наноструктур не изменяет состояния рассеивателя. Процесс взаимодействия ОХН с исследуемым образцом сводится к отражению, преломлению и дифракции нейтронной волны. Это чисто оптические явления, в которых свойства нейтронов определяются ядерным оптическим потенциалом [7; 8; 9]:

V ( r ) = ^ (2 n h ² / m ) bi 5 ( r - r i ) = (2 n h ² / m ) b p ( r ) . (1) i

Здесь h – постоянная Планка; m – масса нейтрона; r – текущая к оордината; r i - положение ядра с номером i ; p ( r ) - плотность частиц рассеивателя; bi (см) - когерентная амплитуда рассеяния на связанном ядре. Величину “ - b_i ” называют длиной рассеяния Ферми. Подавляющее большинство ядер характеризуется положительной длиной рассеяния Ферми, но есть некоторое количество ядер с отрицательной длиной рассеяния. Если bi > 0 , то нейтронная волна как бы выталкивается из области действия ядерного потенциала, а при bi <  0 втягивается в нее^_Суммирование в (1) проводится по всем ядрам рассеивающей системы. Константа b – усредненное значение амплитуды рассеяния. Потенциал V ( г ) определяет показатель преломления среды:

n ² = 1 - V / E , (2)

где E – энергия нейтрона, падающего из вакуума. Источником ОХН является ядер-ный реактор. Однако доля ОХН в спектре реактора очень мала. Таким образом, использование ОХН в спектрометре затруднено из-за существенного возрастания времени измерений поля рассеянных нейтронов. Тем не менее уникальные свойства ОХН привлекают внимание экспериментаторов как у нас в стране, так и за рубежом. В частности, в Физическом институте имени П.Н. Лебедева РАН создан и функционирует на базе ядерного реактора МИФИ времяпролетный спектрометр ОХН [6].

Спектрометр очень холодных нейтронов

Времяпролетный спектрометр, представленный на рис. 1, предназначен для измерений зависимостей полных сечений взаимодействия ОХН с веществом от скорости налетающих из вакуума нейтронов. Исследуемые образцы помещаются в измерительную камеру-криостат. Спектрометрия осуществляется по времени пролета шестиметровой пролетной базы от механического прерывателя потока нейтронов до детектора. Выделение ОХН из спектра реактора происходит в вакуумируемом ней-троноводе. ОХН, отражаясь от его стенок, выводятся из пучка более быстрых и не отражающихся от стенок нейтронов. В качестве источника нейтронов используется бериллиевый конвертор, смещающий спектр нейтронов в область меньших энергий, расположенный в ячейке активной зоны реактора. В непосредственной близости от измерительной камеры находится счетчик – монитор потока нейтронов. Измерения производятся с образцом и без него для определения падающего N_o и прошедшего через образец N_tr потоков нейтронов.

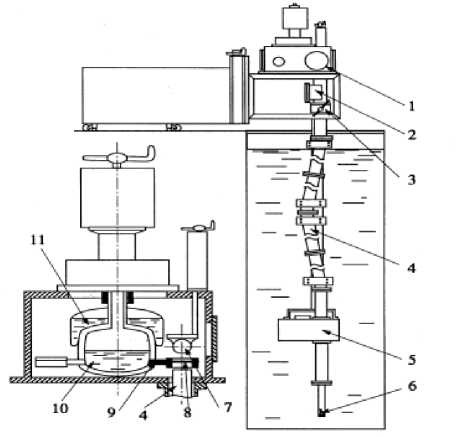
Рис. 1. Схема спектрометра.

1 – камера криостат; 2 – монитор; 3 – шибер; 4 – нейтроновод; 5 – прерыватель;

6 – конвертор; 7 – счетчик; 8 – образец; 9 – держатель образца;

10 – низкотемпературная ванна; 11 – азотная рубашка

Макроскопическое полное сечение ослабления Σ _t определяется отношением прошедшего потока излучения к падающему потоку:

S t = (1/ x )ln( No I Nr ).

В формуле (3) x – это толщина образца. Скорость нейтрона в вакууме v определяется по времени пролета из соотношения t = -^( v I g )² + 2 L I g - ( v I g ) . В качестве детектора нейтронов используется специальный ³Не-счетчик с давлением гелия 500 тор и эффективностью регистрации ОХН ∼ 100%. Такой детектор практически не чувствителен к тепловым нейтронам.

Поскольку ОХН обладают ярко выраженными оптическими свойствами, то при определении полного сечения необходимо вводить поправки на преломление нейтронной волны на границе вакуум/образец и на многократное отражение от границ

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

образца. Первая поправка сводится к вычислению эффективной скорости нейтрона в образце v': v'=7 v2 - v2,                                    (4)

где v_r – граничная скорость для вещества, при которой происходит полное отражение нейтронов при любом угле падения на образец. Методика введения второй поправки более сложна и подробно описана в работе [6].

Рассмотрим теперь составляющие полного макроскопического сечения взаимодействия ОХН с веществом S t :

S t = S c + S ^ + S H + S es .                            (5)

Здесь S _c - сечение захвата нейтрона; S e - сечение неупругого рассеяния нейтронов на колеблющемся в тепловом равновесии ядре исследуемого вещества; S H - сечение упругого некогерентного рассеяния на ядрах вещества; S _es - сечение упругого рассеяния на неоднородностях ядерного оптического потенциала рассеяния. Неупругое рассеяние приводит к нагреванию нейтронов. Поскольку эффективность регистрации тепловых нейтронов детектором много меньше эффективности регистрации ОХН, сечение неупругого рассеяния рассматривают как сечение поглощения наряду с сечением захвата ( S c + S e ) w (1 / v ) . Сечение упругого некогерентного рассеяния не зависит от скорости нейтрона и определяется исключительно рассеивающими свойствами ядер исследуемого вещества. Известная зависимость перечисленных сечений от скорости нейтрона позволяет исключить из полного сечения вклад чисто ядерных и неупругих процессов взаимодействия и выделить зависимость сечения упругого рассеяния ОХН на элементах наноструктур от скорости нейтронов.

Теоретические основы метода рассеяния ОХН

Фундаментальная величина в нейтронной оптике - это когерентная волна, ^ ( r ) • Она обеспечивает полное описание всех когерентных упругих процессов рассеяния и удовлетворяет уравнению Шредингера [8]:

|^ ( h ² / 2 m ) А + V ( r )^( r ) = E ^ ( r ) ,                       (6)

V(r) = (2nh2 / m)^bi < 8(r - ri ) >= (2nh2 / m) < b(r) >= (2nh2 / m)pbS(r), (7) i f 1, при r eQ где S(r) = <             - функция формы, О - объем рассеивателя.

[ 0, при r gQ

В уравнениях (6) и (7) V ( r ) - это оптический потенциал в кинематической теории рассеяния; E – энергия падающего нейтрона; m – масса нейтрона. Потенциал V ( r ) и решение ^ ( r ) - это макроскопические величины, зависящие только от термодинамического состояния системы. В газах, жидкостях и аморфных твердых телах потенциал V ( r ) - константа. В кристаллах - плавно меняющаяся периодическая функция r . Ее период равен периоду решетки.

Сечение рассеяния ОХН может быть вычислено в случае, когда поле, на котором происходит рассеяние, может рассматриваться как возмущение, а в качестве возмущения берется полная потенциальная энергия частицы во внешнем поле: потенциальная энергия нейтрона в среде V ( r ) (1). Такой метод в теории столкновений называют борновским приближением [10]. Оно возможно при выполнении условия

|V\ <<  Й v / a = Й ² к ²/ mak = E! ak .                      (8)

Здесь a - радиус действия поля V ( r ) ; V - порядок величины потенциальной энергии нейтрона в основной области ее существования.

Условимся различать рассеяние ОХН на отдельной частице [12] и рассеяние на флуктуациях среды (например, флуктуации плотности или магнитной индукции). Во многих реальных случаях невозможно сказать что-либо определенное о форме неоднородностей. Моделировать рассеяние в таких средах удобно, подобрав корреляционную функцию, адекватно отражающую реальный процесс рассеяния. Данные об общих свойствах корреляционной функции можно получить из анализа зависимостей макроскопического сечения от волнового числа k [13–15].

Дифференциальное сечение упругого рассеяния ОХН на неоднородностях образца в борновском приближении теории возмущений имеет вид [13–15]:

d ( S I ) d О

m^ I ff K 8 V 8 v( r I r ' )e^{1 q ( r - r} ) d r d r ' (см 2 ).

2 n h J

Здесь S _es (см^-1) - макроскопическое сечение упругого рассеяния; V - объем образца; 8 V ( r ) = V ( r ) - <  V >  - флуктуация рассеивающего потенциала; K ₈ V ₈ V . ( r | r ' ) = = < 8 U ( r ) 8 U ( r ' ) >  - корреляционная функция флуктуаций 8 V ( r ) и 8 V ( r ' ) ; q =

= k - k', k и k' - волновые векторы нейтронов до и после рассеяния соответственно, m – масса нейтрона. В случае изотропной и однородной среды корреляционная функция зависит только от модуля разности векторов p =| r - r' |, а дифференциальное d Sm сечение es d О

оказывается зависящим только от модуля передаваемого нейтрону им- пульса [13, 14]:

d S es d О

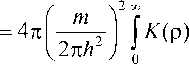
sin q p 2 , ------p d p .

q p

Интегральное сечение рассеяния

( dSA   2n 2kk ( dSA     ( m V 8n2 ”

S„ =   —es d О = —у —es- qdq = --- _T —^ K ( p )(1 - cos 2 k p ) d p .

^es 4 d О J k ² J ( d О Г 1 2 n h ² J k ² J

При учете размеров детектора нейтронов вместо (11) мы будем иметь:

2A k < dУ A < m. A2 8^2 ^

2es=I \^\qdq=Itt212"^"JK(p)[cos(2kpSo)"cos2kp]dp, (12) k k sin 00 V d^)      V 2ЛЙ ) k 0

где 2 9 ₀ - угол, под которым «виден» детектор нейтронов из образца; S ₀ = sin 0 _О .

Во многих случаях невозможно сказать что-либо определенное о форме неоднородностей. Моделировать в таких средах можно, подобрав соответствующий коррелятор, адекватно отражающий реальные процессы рассеяния в случайно неоднородных средах. Один из наиболее употребляемых корреляторов – экспоненциальный (пуассоновский) коррелятор, для которого корреляционная функция имеет вид:

K ( R ) = K (0)exp( - R / lc ) .

Здесь R =| r 1 - r ₂ | , l_c - корреляционная длина, K (0) = ф (1 - ф )( Ap )² .

Величина l_c = J ” K ( p ) d p / K (0) называется длиной корреляции возмущения [15] и определяет эффективный размер неоднородностей; ф - объемная доля рассеивателей; Ap = ( Nb - Njbj ) - перепад длин рассеивающей плотности на границе рассеи-ватель/матрица. Рассматриваемая статистическая модель

K ( rjr 2 ) = K (0) N ( rjr 2 )

должна быть устойчивой по отношению к изменению вида коэффициента N ( r 1 | r ₂) . Можно полагать, что имеется некоторый класс функций, внутри которого изменение

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

вида коэффициента корреляции не влияет на основные результаты. В данном случае такой класс функций образуют функции N ( r 1 | r ₂) , имеющие отличную от нуля первую производную при |r 1 - r ₂ 1 = 0 . Другой хорошо известный и широко используемый коррелятор – гауссовский:

K ( R ) = K (0)exp( - R I lc )² .                       (15)

Для пуассоновского коррелятора из соотношения (12) получим

S es = (8 п ²/ к ²) K (0) lc [ (1 + 4 к ² lc ²sin² 0 о ) ^{- 1} - (1 + 4 к ² lc ²) ^{- 1} ] ,      (16)

а для гауссовского коррелятора

S es = (8 п ²1 к ²)( n ^1/2 K (0) lc ) [ exp( - 4 к ² lc ²sin² 0 о ) - exp( - 4 к ² lc ²) ] . (17)

Дифференциальное макроскопическое сечение рассеяния d S _es I d Q ОХН на N изолированных рассеивателях, заключенных в объеме V _Q , имеет вид:

( d S es I d Q ) = ( d S' I d Q ) N I V q = Vp ² ( p p - p _s )² P ( q ) 5 ( q ) N I V .   (18)

Здесь dS' I dQ - «микроскопическое» дифференциальное сечение рассеяния на отдельно взятом рассеивателе; Vp - объем рассеивателя; q = k - k', k и k' - волновые векторы нейтронов до и после рассеивания соответственно; (pp - p5 )2 = [npbp - nsbs ]2 ^ т - контраст рассеивателя-матрицы; P(q) - форм-фактор рассеивателя; S(q) - структурный фактор центров частиц, связанный с корреляцион ной функцией Ван Хова G(r) [7]:

-12

^{P (} q )=^ ^p

j exp ( i qr ) d r

V p

, P (0) = 1;

2\

5 ( q ) = — N

Ze-iKr-rj) \ = jG(r) eiqrdr, g(r) = 6(r) + Gd(r), (20) l, j / где функция Gd (r) может быть выражена через парную корреляционную функцию [7]; q - передаваемый импульс; 0 - угол рассеяния; q = 2кsin(012), угловые скобки означают усреднение по ансамблю.

Для наночастиц различной формы (изолированные сферы, цилиндры, в том числе полые, эллипсоиды и т.д.) в работах [11; 12; 16; 17] с помощью уравнений (18), (19) из соотношения (11) получены полные сечения рассеяния S _es . При этом учтено, что S ( q ) ^ 1 для больших углов рассеяния.

Главная трудность в применении наночастиц при создании новых материалов – их склонность к агломерации. В частности, макроскопические свойства нанокомпози-ционных материалов зависят от равномерности распределения частиц наполнителя в матрице полимера. Кроме того, многие случайные среды являются фрактальными структурами. Частицы-рассеиватели организуются в кластеры. Кластер имеет внутреннюю структуру, описываемую на языке фракталов. Оказывается, что кластеры часто имеют значительную степень самоподобия. Для описании геометрического расположения частиц в кластере используется фрактальная размерность D . Теория фракталов позволила ввести новые количественные показатели структур в виде фрактальной размерности. Рассматриваются массовые (1 <  D V <  3) и поверхностные (2 <  D_s <  3) фракталы. Для простейшей фрактальной среды со структурами порядка ^ , созданных из дискретных рассеивателей размером R ₀ <  r <  ^ , R ₀ <<  ^ , корреляционная функция плотности имеет вид [27]:

< p ( r ) р (0) >= ф (1 -ф )( N 1 b - N 2 b ₂)²( D v /4 n )exp( - r / ^ )( R 0 / r )^{3 -} D ^V . (21)

Среда предполагается изотропной и однородной в среднем, и корреляционная функция тогда зависит только от модуля разности векторов r = |r 1 - r ₂|; (1 -ф ) -часть объема образца, занятая фракталами; D_V – размерность объемного фрактала; N_ib_i – длины ядерных плотностей. В борновском приближении, учитывая (9), (10), дифференциальное сечение упругого рассеяния фракталом принимает форму:

d ° es dQ

= j < p (0) p ( r ) >  e ^{q ( r 1} r ^{2 )} d r 1 d r ₂ =

= ф (1 -ф )( N i b i - N 2 b 2 )² DRR o^{3 -} d^v

D v Г ( Dv - 1)sin [ ( Dv - 1)arctg( q £ ) ] (4 n )² q ( q ² + ^^{- 2})⁽ D V ^{- 1)/2}

где VD_v = V ₃( R ₀ / y³ D V , V₃ = ^ ³ , Г ( x ) - гамма-функция; q = 2 k sin( 0 /2) - переданный импульс; k - волновое число; 0 - угол рассеяния. Полное макроскопическое сечение упругого рассеяния получено нами из (11) и (22) соответственно.

^ es

ф (1 -ф )( N 1 b 1 - N ₂ b ₂)² d v

8 п R 0 D ^{V - 3} к^г

Г ( D_V - 2) ^ D ^{V - 2}

cos[( D v - 2)arctg(2 к ^ )] .       (1 + 4 k² ^)⁽ d v ^{- 2)/2}

. (23)

Исследование неорганических материалов

В работах [19; 20] исследованы микропреципитаты промышленных бездислока-ционных монокристаллов p-Si, выращенных методом Чохральского (с концентрацией бора 1,5·10¹⁶, 2·10¹⁸, 2·10¹⁹), и монокристалл с ρ = 3 ком·см, полученный методом бес-тигельной зонной плавки. Кроме рассеяния ОХН были использованы современные методы: лазерная масс-спектрометрия, масс-спектрометрия вторичных ионов. Получены следующие результаты. В монокристалле Si, выращенном методом Чохральско-го, содержатся неоднородности:

• а)    обнаружено, что в объеме содержится большая концентрация ≥10¹⁸см^–3 О и Н, находящихся в свободном и связанном состоянии, причем распределение их неравномерно;

• б)    концентрация металлических примесей находится ниже порога чувствительности лазерной масс-спектрометрии – 10¹⁷ см^–3;

• в)    во всех кристаллах (кроме бестигельного) вне зависимости от концентрации бора обнаружены объемные микропреципитаты с концентрацией 10¹⁴÷10¹⁵ см^–3 и размерами от 6 до 12 нм.

Такая электроактивная примесь может проявить себя самым неожиданным образом на стадии химико-механической полировки, травления пластин Si и далее при изготовлении приборов. Совокупность полученных экспериментальных данных позволяет высказать предположение о превалирующей роли O в образовании микропреципитатов и о наличии электрически активного H в кристаллах, выращенных методом Чохральского. В кристалле, полученном методом бестигельной зонной плавки, указанные неоднородности в пределах чувствительности методик не обнаружены [19; 20].

Исследована наноструктура систем PdH χ ( χ = 0,008; 0,105; 0,26; 0,32; 0,51; 0,71), PdD₀₆ [21], металлического урана [22]. Определены такие параметры, как эффективный р^, азмер элементов структуры, их концентрация, форма, распределение по размерам; их изменения в зависимости от различных физических условий (температура измерений, тепловая обработка изучаемого материала).

Исследования гидрида и дейтерида палладия показали, что такими элементами сверхструктуры могут являться зародыши α - и β -фаз. Рассмотрен вопрос зародышеобразования в двухфазной водородосодержащей системе PdH χ .

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

Анализ данных по металлическому урану показал, что рассеивателями очень холодных нейтронов являются поры. Показана их связь с термообработкой.

Впервые измерены зависимости полных сечений взаимодействия ОХН с H2O, D2O от длины волны при разных температурах в диапазоне 291…333 K. Основной вклад в полные сечения взаимодействия ОХН с H2O и D2O вносит сечение неупругого рассеяния [23]. Не обнаружено значительного (>1 012 см–3) числа кластеров плотности в воде в предположении 10% перепада плотности на границе льдоподобного кластера, что свидетельствует в пользу современных представлений о надмолекулярной структуре (НМС) воды как о сплошной и однородной сетке водородных связей.

Исследования органических и композиционных материалов

Впервые разработанная нами методика полных сечений ОХН применена для изучения сложной НМС и динамики кристаллизующихся полимеров [24]. Исследованы образцы ПЭ (полиэтилена) различных марок и технологий изготовления, отличающиеся по степени кристалличности, молекулярной массе и разветвленности основной цепи, температуре плавления, размерам кристаллитов, а также образцы ПТФЭ (политетрафторэтилена), дейтерированного ПЭ и сополимера ПЭ с ПА (полиален). Изучено влияние деформации и охлаждения на НМС и динамику этих материалов. В рамках данных исследований определены эффективные размеры НМС, оценены толщина переходных слоев и перепады плотности на границе кристаллит – аморфная прослойка с учетом степени кристалличности, определенные методом рентгеновской дифракции в больших углах.

Наблюдаемое уменьшение перепада плотности при деформации – одноосной вытяжке – для закаленных образцов по сравнению с медленно закристаллизованными находится в соответствии с современными представлениями о НМС кристаллизующихся полимеров. Наблюдаемая интенсивность упругого рассеяния ОХН на НМС сополимера ПА с ПЭ может быть объяснена, исходя из предположения, что весь ПА при медленном охлаждении в прессе выталкивается в аморфную прослойку.

Анализ неупругого рассеяния ОХН показал, что релаксационный переход в районе Т = 150 К ярче выражен в образцах линейного ПЭ с высокой степенью кристалличности и кристаллитами относительно больших размеров. Подвижность элементов цепи ПЭ при температурах ниже 150…130 К сохраняется в таких образцах, по-видимому, лишь в приповерхностных областях вокруг кристаллитов. Что касается образцов разветвленного ПЭ, подтверждается вывод о высокой подвижности CH3 – групп при низких температурах.

Впервые проведенные исследования веществ, обладающих упорядоченной НМС (блок-сополимер ПС – ПБ – ПС (полистирол-полибутадион-полистирол), ЛЖК (50% водный раствор додецилоксиэтиленгликоля)), показали, что когерентное рассеяние ОХН на сверхструктурах с характерными размерами порядка длины волны ОХН является практическим и естественным методом их изучения [25; 26]. Измерения Σ _t( λ ) по пропусканию ОХН с применением дейтериевого контраста позволили наблюдать фазовые превращения ЛЖК в зависимости от температуры и его состава. Были определены типы сверхрешеток, параметры порядка, их трансформация при изменении температуры и состава даже в оптически изотропной фазе, где применение традиционных оптических методов невозможно.

В результате впервые проведенных измерений отражения ОХН от сверхструктуры блок-сополимера ПС – ПБ – ПС при двух постоянных углах отражения и переменной длине волны [25], а также зависимостей Σ _t( λ ) по пропусканию пучка нейтронов через образец определены межплоскостные расстояния гексагональной решетки полистирольных цилиндров в полибутадиеновой матрице, средний размер областей упорядоченности, диаметр полистирольных цилиндров, степень дефектности сверхкристалла.

Методом отражения очень холодных нейтронов (ОХН) исследована структура полимерного покрытия, выращенного на полированной поверхности монокристалла Si, предварительно активированной катализатором [27]. Получены зависимости (от длины волны ОХН) коэффициента отражения ОХН от образца – кремний/полидейтеро-этилен/полиэтилен (Si/PDE/ПE) – как со стороны подложки, так и с внешней стороны полимерного покрытия. Проведено сравнение с полученными ранее данными для образца кремний/полидейтероэтилен (Si/PDE). Определены размеры аморфно-кристаллической структуры PDE внутри слоя, средняя глубина шероховатостей на отражающих поверхностях PDE.

Показано, что по мере удаления от подложки структура PDE меняется от хорошо упорядоченной (вблизи поверхности кремния) до стандартной аморфно кристаллической структуры полиэтилена в блоке на границах вакуум/PDE и ПE/PDE. Кроме того, обнаружено, что глубина шероховатостей на границе ПE/PDE меньше, чем на границе вакуум/PDE, возможно, за счет «давления» слоя ПE при синтезе PDE-покрытия под слоем ПE. Результаты исследования подтверждают возможность получения композитов с высокой степенью наполнения, в которых полимерная компонента сосредоточена в слоях толщиной несколько сотен нанометров вокруг частиц наполнителя. Структура такого покрытия отличается от структуры полимера в блоке большей упо- рядоченностью упаковки макромолекул.

При получении нанокомпозиционных материалов одной из основных трудностей является процесс агломерации наночастиц наполнителя. Спектрометр ОХН был применен [28] для разработки метода получения нанокомпозитов с полиолефиновой матрицей, наполненной наночастицами различных веществ. В частности, были исследованы образцы полиэтилена, наполненные частицами алюмосиликатов, методом интеркаляционной полимеризации. Суть метода заключается в заполнении межслойного пространства природных минералов типа монтмориллонита (ММ) катализатором с последующей полимеризацией, которая приводит сначала к разбуханию, а потом к разрушению (эксфолиации) слоистой структуры ММ. Степень эксфолиации (относительная объемная доля наночастиц ММ в полиэтиленовой матрице) определялась с помощью рассеяния ОХН. В результате проведенных исследований было показано, что степень эксфолиации зависит от предварительной обработки (интеркаляции) ММ и подбора системы интеркалянт-катализатор. Увеличение доли ММ приводит к значительному уменьшению газопроницаемости (рис. 2) по сравнению с чистым полиэтиленом (Pc/Po), что позволяет использовать этот наноструктурированный материал для транспортировки газа.

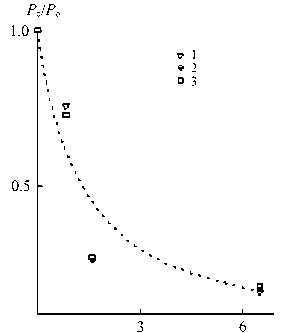
Рис. 2. Зависимость газопроницаемости композита ММ/ПЭ от объемной концентрации ММ (1 – N2, 2 – O2, 3 – CO2, • • • Theory)

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

Были исследованы процессы агломерации наночастиц наполнителя в композиционных материалах на базе полиолефинов [29; 30]. В частности, были изучены структуры композиционных материалов СаСО3/полипропилен (СаСО3/ПП) и нанокомпозита на основе полипропилена и многослойных углеродных нанотрубок (МСУНТ/ПП).

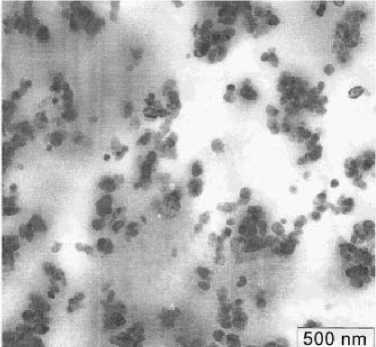
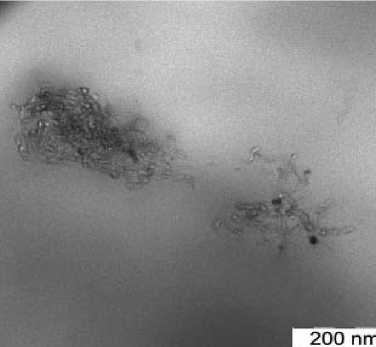
а                                                  б

Рис. 3. Снимки СаСО₃/ПП ( а ) и МСУНТ/ПП ( б ), полученные с помощью туннельного электронного микроскопа (ТЭМ)

ТЭМ-снимки уже дают представление о проблеме агломерации наночастиц наполнителя, однако они сделаны на малом участке площади исследуемого образца. Для получения (что необходимо) усредненных по всему материалу параметров было использовано рассеяние ОХН.

Зависимость доли изолированных нанотрубок от метода подготовки наполнителя (модифицированные и немодифицированные трубки) не обнаружена. Однако объемная доля изолированных трубок большего диаметра уменьшается с ростом содержания от 1 до 3 массовых процентов. При использовании трубок меньшего диаметра объемная доля изолированных трубок заметно уменьшается по сравнению с образцами композита с трубками большего диаметра. Показано, что наибольший процент (90%) изолированных частиц в матрице для вышеперечисленных образцов достигнут в образцах CaCO3/ПП при малых концентрациях наполнения независимо от диаметра частиц наполнителя. Определенные методом ОХН внешние радиусы нанотрубок близки к средним значениям, указанным изготовителем. Значения толщины стенок трубок (R1–R2) колеблятся в пределах 5–7 нм для нанотрубок серии NT(K3) и 3 нм для NT(K1) и не зависят от метода подготовки наполнителя (модифицированные и немодифицированные трубки). Эти величины близки к значениям, полученным методом рентгеновской дифракции на рентгеновском дифрактометре Центра коллективного пользования «Ускорительный центр нейтронных исследований структуры вещества и ядерной медицины ИЯИ РАН». Зависимость доли изолированных нанотрубок от метода подготовки наполнителя (модифицированные и немодифицирован-ные трубки) не обнаружена. С другой стороны, объемная доля изолированных трубок уменьшается с ростом содержания NT(K3) от 1 до 3 массовых процентов. При использовании трубок меньшего диаметра NT(К1) в образцах композиций NT(K1)-17 и NT(K1)-18 объемная доля изолированных трубок заметно уменьшается по сравнению с образцами серии NT(K3). Определенные значения фрактальной размерности

D (2,8–2,87) указывают на большую плотность частиц CaCO3 в агломерате. Не обнаружено влияние ПАВ на степень агломерации частиц наполнителя.

Исследование взаимодействия ОХН с ферромагнетиками

Измерение зависимостей Σ _t( k ) осуществлялось на времяпролетном спектрометре ОХН в широком диапазоне 10^–1<  k ₀< 10⁰ нм^–1 с образцами ⁵⁸Ni и Fe при температуре 298 K, охлажденными до 80 K [31]. Исходя из различия полученных кривых для ⁵⁸Ni, был оценен вклад неупругого рассеяния Σ _ie в полные сечения при комнатной температуре. Из анализа зависимости Σ _ie( k ₀) следует, что она с достаточной точностью подчиняется закону ~ 1/k₀. На образцах Fe, однако, в пределах точности измерений выделить зависимости Σ _ie( k ₀) не удало сь. Общим для зависимостей Σ _t( k ₀) является наличие существенного отклонения от закона ~ 1/ k ₀ в сторону увеличения сечений. Нечувствительность отклонений к температуре дает основание считать, что они определяются упругим рассеянием ОХН на структурных неоднородностях образца. Так как Ni и Fe – ферромагнетики, то можно предположить, что неоднородности имеют магнитную природу. Для проверки этой гипотезы были проведены измерения зависимостей Σ _t( k ₀) при действии на образец магнитного поля различной величины. Образец ⁵⁸Ni измерялся без магнитного поля и при намагничивании в поле H = (0,92; 1,72; 4,76; 8,44)∙10⁴A/м, а Fe – в поле 6∙10⁴A/м и без поля. Из рассмотрения приведенных результатов видно, что зависимости Σ _t( k ₀) сильно зависят от величины магнитного поля: при увеличении H сечения уменьшаются. Однако для нейтронов с k ₀ ≤ 5∙10^–1 нм^–1 даже при напряженностях поля Н , приближающих Fe и ⁵⁸Ni к состоянию предельной намагниченности, полностью подавить упругую составляющую не удалось. При этом, если в случае Fe для всех четырех образцов наблюдался участок Σ _t( k ₀) ~ 1/ k ₀ даже при H = 0, то в случае ⁵⁸Ni подобный участок проявился при H = 1,72∙10⁴ А/м.

Характеристики статических магнитных неоднородностей в исследованных образцах определялись аппроксимацией экспериментальных зависимостей Σ _es( k ) асимптотическими выражениями и точными формулами. Результаты находятся в удовлетворительном согласии друг с другом. Исследования ⁵⁸Ni, проведенные в широком диапазоне Н , позволили проследить динамику изменения размера неоднородности l и флуктуации магнитной индукции <  Δ B ² >^1/2с изменением H . Обе величины, характеризующие магнитные неоднородности, уменьшаются при увеличении H . Экстраполируя l и <  Δ B ² >^1/2 по линейному закону из области H = (1,72…8,47)∙10⁴А/м в область больших значений H , можно оценить предельную величину магнитного поля, при котором магнитные неоднородности исчезают. Она составляет приблизительно 5∙10⁴ А/м.

Проведенное исследование образцов Fe дало несколько отличающиеся результаты от полученных на ⁵⁸Ni. Так, например, при общем уменьшении <  Δ B ² > ^1/2 при увеличении H длина корреляции (размер магнитной неоднородности) l увеличивается. Можно предположить, что этот эффект связан с характерными изменениями в надатомной структуре, происходящими при соответствующей термической обработке. Важным является вопрос: какие дефекты структуры ответственны за образование магнитных неоднородностей? Для его выяснения был проведен анализ зависимости производной намагниченности dJ / dH исследованных образцов ⁵⁸Ni и Fe от H ^–3. В области больших полей H > 4∙10⁴ А/м в дополнение к асимптотическому насыщению намагниченности был обнаружен добавочный механизм намагниченности образцов. Этот механизм в литературе рассмотрен, исходя из предположения о существовании поля механических напряжений вокруг дислокаций, а также из предположения о наличии немагнитных примесных включений и пор. Дефекты такого рода вызывают появление сильной локальной магнитной анизотропии (магнитных неоднородностей), сохраняющейся вплоть до значений магнитного поля ~10⁶ А/м, что находятся в согласии по порядку величины с предельным значением 5∙10⁴ А/м.

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

Определение фундаментальных ядерных констант для элементов и изотопов в диапазоне энергий Е ≤ 10–4 эВ

Впервые в диапазоне энергий 10–4…10–7 эВ определены сечения ядерного захвата нейтронов ядрами Si, Pd, Nb, U, 235U, Fe, 58Ni и др., которые находятся в удовлетворительном согласии с табличными данными в тепловой области [31; 21; 22; 32]. Полученные сечения помещены в Международный банк данных ядерных констант.

Выводы

Метод рассеяния ОХН имеет хорошие перспективы дальнейшего развития как в теоретическом, так и в экспериментальном плане. Для более полной реализации исследовательского потенциала метода идет по стоянное совершенствование теории взаимодействия ОХН с различными конденсированными средами и методов обработки результатов эксперимента.

Представляет существенный интерес рассмотрение рассеяния ОХН в случае невыполнения условий применимости Борновского приближения, т.е. когда размер частицы значительно больше длины волны нейтрона, что может наблюдаться при исследовании, например, композиционных материалов. Авторами с коллегами также показано, что специфические эффекты наблюдаются при рассеянии ОХН фракталоподобными средами, а также сложными планарными и изотропными системами с переходными слоями и т.д.

В экспериментальном плане дальнейшее развитие метода связано с совершенствованием времяпролетной методики спектрометрии ОХН, методов исследования образцов по пропусканию пучка нейтронов и по отражению при постоянных углах отражения и переменной длине волны нейтронов, использованием поляризованного пучка ОХН. Особо следует отметить необходимость увеличения интенсивности потока ОХН, что открывает новые возможности использования ОХН (вплоть до проведения исследований в реальном масштабе времени, например сравнительно медленных релаксационных процессов) и получения более богатой информации. Наиболее верным и перспективным путем в этом направлении является создание специальных источников холодных нейтронов.