Исследования корректности решения задачи круглого ступенчатого оптического волокна с микротрещиной в скалярной постановке

Одним из перспективных направлений повышения эффективности функционирования сетей связи является внедрение прогнозирующих стратегий технического обслуживания волоконно-оптических кабельных линий, в основе которых – мониторинг параметров линии и алгоритмы прогноза интервалов обслуживания по его результатам. В частности, в [1] предложен алгоритм прогноза срока службы одномодовых ОВ по результатам мониторинга локальных отражений на выявленных дефектах. Разработка данного алгоритма потребовала вывода соотношений, описывающих зависимости между геометрическими размерами микротрещины в ОВ и постоянной распространения основной моды на участке ОВ с дефектом.

В [1] предложены приближенные формулы расчета постоянной распространения основной моды и локального коэффициента отражений на микротрещине ОВ. При этом полагали, что

• -    оптическое волокно является слабонаправляющим и можно использовать скалярную постановку задачи;

• -    распределение поля основной моды возмущенного волоконного световода то же, что и для невозмущенного.

Однако, поскольку показатель преломления в области микротрещины равен единице, то есть существенно отличается от показателя преломления кварцевого стекла, вызывает сомнение допустимость применения скалярного приближения. При этом, поскольку микротрещина нарушает осевую симметрию конструкции волновода, следует полагать, что распределение поля основной моды в ОВ с дефектом не будет коаксиальным и будет отличаться от распределения для невозмущенного световода.

Вышесказанное вызывает необходимость проверки корректности сделанных выше допущений и определения области геометрических размеров микротрещины, для которых они справедливы. С этой целью были выполнены вычисления постоянной распространения основной моды круглого ступенчатого ОВ с микротрещиной численными методами – МКЭ в скалярной и векторной постановке задачи на собственные значения. Сравнение полученных в результате вычислений оценок позволяет выявить область изменений параметров микротрещин, для которой при заданных характеристиках ОВ вышеуказанные допущения справедливы. Результаты анализа, полученные при сопоставлении оценок, и представлены в данной работе.

Модель ОВ с микротрещиной

Рассмотрим круглое одномодовое ступенчатое ОВ. Для описания микротрещины воспользовались моделью, представленной в работе [2]. Поперечное сечение световода, для которого выполнялись расчеты, приведено на рис. 1.

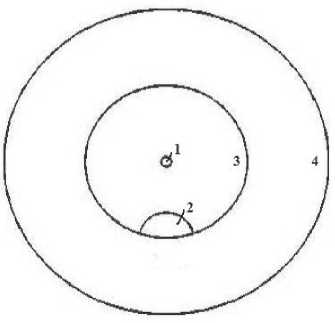
Рис. 1. Поперечное сечение ступенчатого ОВ с микротрещиной: 1 – сердцевина световода; 2 – область микротрещины; 3 – оболочка световода; 4 – первичное защитно-упрочняющее покрытие

Исследования проводились для ОВ типа SMF28e с радиусом сердцевины a = 4,15 мкм; радиусом оболочки 128 мкм и высотой профиля Δ = 0,36%. Значения показателя преломления оболочки из чистого кварцевого стекла и сердцевины из кварцевого стекла, легированного германием, определяли по формулам Селлмейера [3-6] по известной методике [6]. Расчеты выполняли на длине волны 1550 нм, для которой значения показателя преломления кварцевого стекла, легированного германием, для сердцевины и чистого кварцевого стекла принимались равными 1,449616295113657 и 1,444388248968061 соответственно. Значения показателя преломления в области дефекта принимали равными единице, то есть как для воздуха. Значение показателя преломления эпоксиакрилатного покрытия полагали равным 1,4300 [7]. Размеры дефекта задавали параметром г/ = d / a, где d – кратчайшее расстояние от оси ОВ до границы с зеркальной зоной микротрещины; a — радиус сердцевины световода. В соответствии с предложенной в [2] моделью, с учетом геометрических построений (см. рис.2-3), параметры микротрещины рассчитывались по формулам:

r, = b - dp ;

г = b2

4Z>2

^■=b2+r;

r2-/r,

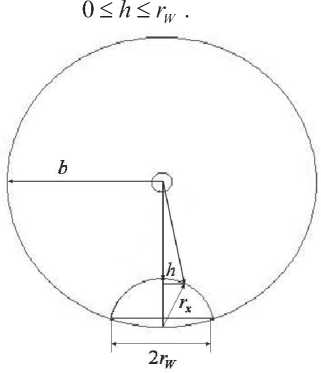
Рис. 2. К расчету геометрии микротрещины

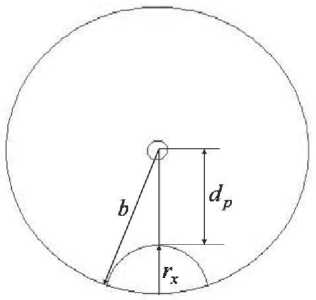
Рис. 3. К расчету геометрии микротрещины

Примеры распределений показателя преломления по сечению ОВ иллюстрируют рис. 4-5.

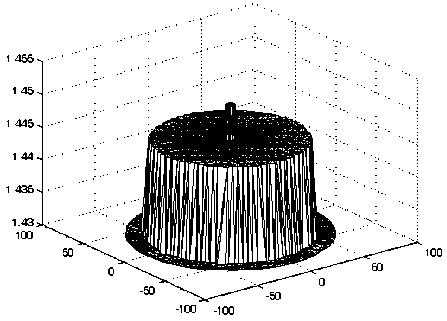
Рис. 4. Распределение значений показателя преломления по сечению ОВ без дефекта

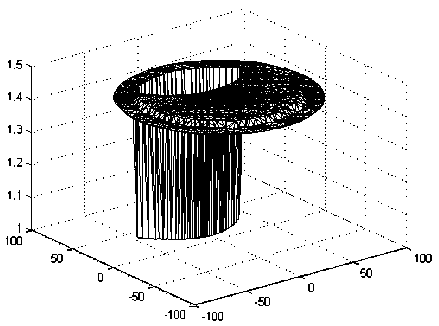
Рис. 5. Распределение значений показателя преломления по сечению ОВ с дефектом при η = 2

Методы вычислений

МКЭ для скалярной постановки задачи реализован в пакете программ PDE (Partial Differential Equations) в комплексе MATLAB. Применение данного пакета позволило получить оценки постоянной распространения основной моды исследуемого световода с приемлемой точностью на обычных персональных компьютерах, исключив разработку специализированного программного обеспечения и применение дорогостоящих пакетов программ.

Как было отмечено выше, для анализа ступенчатого ОВ с дефектом следует применять МКЭ в векторной постановке задачи. Серьезной проблемой здесь является наличие решений, не имеющих физического смысла. Поэтому наиболее перспективным является применение метода смешанных конечных элементов (МСКЭ), исключающего «ложные» решения [8]. МСКЭ предполагает расчет в заданной области трехмерного векторного поля, зависящего от двух пространственных координат, и применяется в тех случаях, когда из каких-либо априорных соображений известна зависимость поля от третьей координаты. Например, как в рассматриваемой задаче, для расчета постоянных распространения собственных мод регулярных волноводов.

В данной работе для вычислений постоянной распространения основной моды ОВ с микротрещиной в векторной постановке задачи использовали пакет программ, разработанный на кафедре ЛС и ИТС ПГУТИ. Программа реализует вариант МСКЭ, предложенный в работе [9], алгоритм реализации которого подробно изложен в [10]. Необходимость учета влияния первичного защит-но-упрочняющего покрытия, поле в котором на некотором удалении от оболочки с большой долей вероятности можно полагать равным нулю, позволило во всех случаях использовать простые нулевые граничные условия.

Результаты вычислений

В таблице 1 приведены значения постоянных распространения и локальных коэффициентов отражений, рассчитанные МКЭ для скалярной и векторной постановки задачи в зависимости от параметра η .

Таблица 1. Значения р и зр

г/ = d 1 а	Р 1/м, мскэ	Р 1/м, МКЭ	5Р %
0,0	5,0571	5,8548	-15,77
0,1	5,3210	5,8549	-10,033
0,2	5,4783	5,8553	-6,8817
0,3	5,8563	5,8562	0,0017
0,5	5,8584	5,8583	0,0017
0,7	5,8603	5,8602	0,0017
0,8	5,8610	5,8609	0,0017
0,9	5,8617	5,8616	0,0017
1,0	5,8621	5,8619	0,0034
1,2	5,8632	5,8631	0,0017
1,5	5,8637	5,8636	0,0017
1,7	5,8639	5,8637	0,0034
2,0	5,8640	5,8638	0,0034
5,0	5,8641	5,8639	0,0034
10,0	5,8641	5,8639	0,0034
15,0	5,8641	5,8639	0,0034

Как видим, что для η > 0,3 расхождение значений постоянной распространения, полученных при векторной постановке задачи и скалярной постановке задачи, не превышает 0,004%.

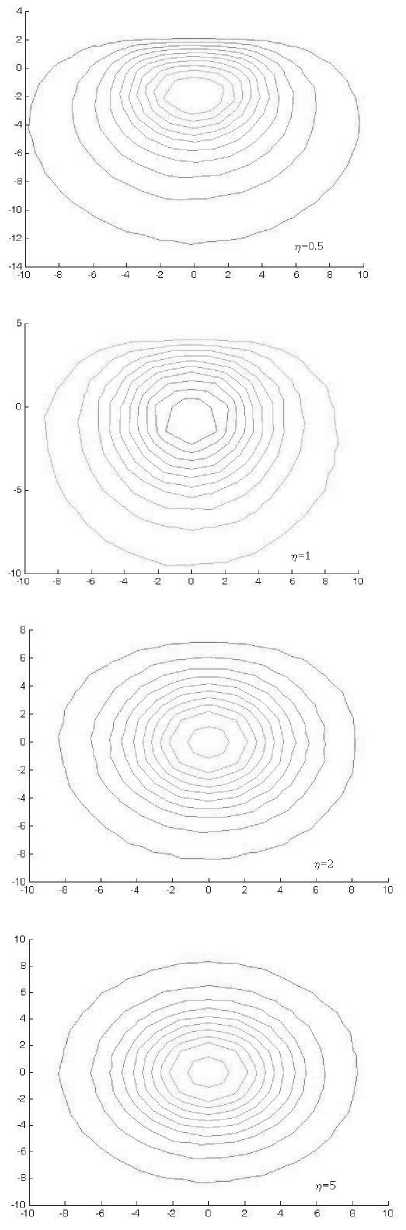
Рис. 6. Распределение мощности основной моды оптического излучения по сечению круглого ступенчатого ОВ с микротрещиной в зависимости от размеров микротрещины (параметр η )

Это позволяет полагать световоды с микротрещиной в данной области ее размеров слабонаправляющими и использовать скалярную постановку задачи. На рис. 6 приведены результаты вычислений распределений абсолютной величины напряженности поля по сечению ОВ с микротрещиной в зависимости от размера дефекта. Учитывая полученные ранее результаты, здесь для вычислений использовали МКЭ в скалярной постановке.

Как видим, в области размеров микротрещины, в которой следует учитывать ее влияние на постоянную распространения световода, распределение поля моды по сечению волокна не является коаксиальным и существенно отличается от распределения для невозмущенного световода.

Заключение

В работе представлены результаты вычислений постоянной распространения основной моды круглого ступенчатого оптического волокна (ОВ) с микротрещиной методом конечных элементов (МКЭ) для скалярной и векторной постановок задачи. Показано, что для η > 0,3 расхождение значений постоянной распространения, полученных при векторной постановке задачи и скалярной постановке задачи, не превышает 0,004%, что позволяет использовать в данной области скалярное приближение. Выявлено, что в области размеров микротрещины, в которой следует учитывать ее влияние на постоянную распространения световода, распределение поля моды по сечению волокна не является коаксиальным и существенно отличается от распределения для невозмущенного световода.