Исследования нестационарных периодических процессов аэробной очистки сточных вод ЖКХ активным илом в циклотенках

Создание эффективных систем локальной биологической очистки сточных вод малых жилых комплексов, индивидуального жилья и объектов сервиса остается актуальным для развивающегося рынка продукции и услуг данного вида в современной России. Наиболее широкое применение нашли системы биологической очистки сточных вод проточного типа – аэротенки и биофильтры, работающие в квазистационарных режимах. Нестационарность работы последних проявляется лишь в неравномерностях колебаний расхода, состава сточных и т.п., имеющих суточный и сезонный характер. Эти колебания имеют, как правило, ограниченную амплитуду и не оказывают заметного влияния на рабочие параметры больших систем, применяемых на крупных станциях чистки сточных вод. Методы расчета параметров стационарных процессов2 в таких системах хорошо отработаны [7], а для нестационарных ограничено лишь изучением динамических откликов выходных параметров, характеризующих качество очистки, на флуктуации входных параметров сточной воды с целью определения оптимальных методов управления.

Опыт стационарных процессов биологической очистки в установках проточного типа перенесен и на малые установки, несмотря на то, что здесь на снижение качества очистки сильнее сказывается влияние амплитуды различных флуктуаций. На малых объектах водоотведения ее значения значительно выше.

Известен опыт применения установок небольшой производительности с аппаратами периодического действия для аэробной очистки хозяйственно-бытовых сточных вод активным илом в Германии. Однако в литературе отсутствуют опубликованные методики инженерных расчетов таких сооружений, хотя и не встречаются негативные отзывы на эффективность таких систем очистки. Кроме того, имеются достаточно веские основания предполагать, что системы очистки такого типа окажутся эффективнее и поэтому более предпочтительны к применению на малых объектах водоотведения.

Разработанные в лаборатории «Очистные установки и сооружения» ИЭРиОС блочные установки могут представлять интерес для потенциальных потребителей данного сегмента рынка. Среди них:

• •    установки типа "Триос", в составе которых применяются аппараты – фильтротенки для глубокой очистки и доочистки сточных вод, протекающих при биофильтрации в слоях аэрируемой затопленной загрузки;

• •    блочные установки типа "Триос ЦФ", в составе которых имеются аппараты – аэротенки циклического действия (циклотенки) и фильтротенки.

Теоретические предпосылки исследований

Установки аэробной биологической очистки периодического действия, или периодические аэротенки – циклотенки, включают в себя аппараты переменного рабочего объема, в которые в течение рабочего цикла поступает сточная вода на биологическую очистку активным илом. По окончании заполнения и завершении каждого цикла очистки аппарат разгружают: отводят очищенную сточную воду и отдельно – осадок.

При наличии достаточно интенсивной аэрации в первом приближении можно считать такой аппарат аэробным биореактором полного смешения с переменным объемом [1]. В качестве допущения можно принять постоянство концентрации растворенного кислорода в рабочем объеме и во времени. Для нестационарного процесса аэробной очистки сточных вод активным илом в аппарате полного смешения имеем модель [2]

}

(1),

v • XO + ДS, X, CL )• X • V=v • X+V • dX v• Sn -a • ДS,X,C)• X• V=v• S+V•—

OS    L dt где v – объемная скорость потока сточных вод, м3/ч;

• V – рабочий объем, м³;

• t – время, ч;

S – концентрация обобщенного загрязнителя в рабочем объеме, г БПК/м3;

X – концентрация микроорганизмов активного ила, или доза активного ила в рабочем объеме, г активного ила/м3;

SO, XO – концентрация обобщенного загрязнителя и доза активного ила в потоке поступающих в аппарат сточных вод соответственно;

C L =const – концентрация растворенного кислорода в рабочем объеме, г/м³ (это условие заменяет уравнение нестационарного баланса растворенного кислорода, присоединенное к системе уравнений модели в первоисточнике [2], что отвечает принятому ранее упрощающему допущению;

• ^ (S,X,C L ) - удельная скорость роста микроорганизмов активного ила, г/м³ ' ч;

• a s - стехиометрический коэффициент утилизации органических загрязнений, г БПК/

г ила.

Первое уравнение системы (1) описывает нестационарный динамический баланс концентрации микроорганизмов активного ила, а второе уравнение – динамический баланс обобщенного органического загрязнения сточных вод. Легко доказать, что система может быть применена как для открытых систем проточного типа, где V=const, а v, XO и стр. 120 из 233 SO могут быть переменными во времени; так и для систем периодического действия, в которых все указанные величины могут быть переменными во времени, а рабочий объем – неубывающая функция времени.

То, что в динамическом балансе клеточного роста неучтен механизм отмирания клеток микроорганизмов активного ила – так называемый процесс самоочищения активного ила, является недостатком модели (1). Более детально и точно описывают процессы клеточного роста и самоочищения микроорганизмов активного ила, утилизации им органических загрязнений кинетические уравнения модели Герберта [1,7]

dS dt

-α⋅µ _m

S⋅X

⋅

K 1 + S

dX

=µ _m dt

S⋅X

⋅

K ₁ + S

K 2

⋅X

}

В модели Герберта (2) удельная скорость роста микроорганизмов активного ила – первый член в правой части второго уравнения описывается формулой Моно [2; 3], скорость самоочищения пропорциональна дозе активного ила – второй член правой части второго уравнения. Таким образом, второе уравнение модели (2) дает описание суммарной скорости микробиологического баланса. Эта скорость может быть положительной, отрицательной или равной нулю, а скорость утилизации органических загрязнений описывается первым уравнением. Она пропорциональна скорости клеточного роста: в качестве коэффициента пропорциональности выступает стехиометрический коэффициент α. Коэффициенты уравнений в модели (2) предлагается определять экспериментально в зависимости от вида сточных вод. Вавилин и Мозер [2] экспериментально определили значения коэффициентов модели (2) (табл. 1), однако не указали точное происхождение и тип исследованных сточных вод, поэтому приведенные данные могут служить примерным ориентиром.

Таблица 1

Экспериментальные значения коэффициентов модели

Автор	-1 µ m , ч	α , г БПК/г ила	К 1 , г БПК/м3	К 2 , ч-1
Вавилин	0,11	2	100	0,005
Мозер	0,09	1,67	400	0,02

Можно заметить, что введение в модели (1) и (2) функции удельной скорости утилизации обобщенного органического загрязнения сточных вод в виде: ρ (S,X,C L )= α s ^. µ (S,X,C L ) (3)

позволяет выразить скорость клеточного роста через функцию скорости утилизации обобщенного загрязнителя

H(S,X,Cl)=Ys p(S,X,Cl) , где Ys=as-1 - стехиометрический коэффициент прироста активного ила, г ила/г

БПК.

Моделирование установившихся периодических процессов аэробной биологической очистки

Циклотенк представляет пару аппаратов аэробной биологической очистки периодического действия, находящиеся в противофазном режиме работы: в момент, когда в одном аппарате рабочий цикл завершается сливом, а в другом начинается заполнение. Обобщенно рабочий цикл можно представить состоящим из 4-х фаз: заполнение, сохранение постоянного объема, отстаивание, слив. Фазы заполнения и постоянного объема объединяются в фазу аэрации, причем в рассматриваемой модели фаза постоянного объема может отсутствовать. Условием, необходимым для организации непрерывной работы циклотенка, является неравенство

• t 3 >  t c + t i + t o ,                                                                               (5)

где t 3 , t C , t I , t O – время заполнения, постоянного объема, отстаивания и слива.

Отношение продолжительности фазы постоянного объема и фазы заполнения назовем коэффициентом структуры временного цикла фазы аэрации, или просто структурным коэффициентом

tC

T                                                                                               ,

t3

причем из-за необходимости выполнения условия (5) - 0 < т < 1 длительность фазы аэрации и ее составляющих с учетом (6) связаны соотношениями tair = t 3 + tc t3

t.

air

• 1    + т

  t

  
  

  C

  
  

  ^t air

  
  

  •т

  
  

  1 + т

  
  

Модель процесса биологической очистки сточных вод в циклотенке в фазе аэрации строим на основе модели (1) с учетом по модели Герберта (2) скорости самоочищения активного ила, применяя замену уравнения скорости клеточного роста уравнением скорости утилизации органических загрязнений по формуле (4). Для фазы заполнения модель принимает вид dS = D-(So-S)-p(S,X,Cl )• X

—=d^(xo dt O

- X)+

Y S

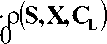
• X - — • X 24

}

где t – время, ч.;

S, S O – концентрация органического загрязнения в рабочем объеме и в поступающих сточных водах, мг БПК/л;

• X, X O – доза активного ила в рабочем объеме и в поступающих сточных водах, г/л;

С L – концентрация растворенного кислорода в объеме, мг/л;

Y S – стехиометрический коэффициент прироста активного ила, г ила/г БПК;

b – коэффициент скорости самоочищения активного ила, сут-1;

D – коэффициент разведения, ч-1.

Коэффициент разведения определяется как отношение объемной скорости, или объемного расхода поступающих в циклотенк сточных вод к рабочему объему [2; 3].

В случае системы с переменным объемом коэффициент разбавления – величина, зависящая от времени. Если объемный расход поступающих в циклотенк сточных вод принять постоянным, то выражение зависимости коэффициента разведения от времени в фазе заполнения примет вид

D = -

V

v

V min

+ v • t ,

где V min – минимальный начальный рабочий объем, м³; v – объемный расход поступающих сточных вод, м³/ч.

t – время, ч.

Если принять минимальный рабочий объем кратным объемному расходу, т.е.: Vmin = k • v, где k - кратность начального заполнения рабочего объема, ч-1, то выражение (8) преобразуется к виду D = —-—.

k + 1

При организации рециркуляции активного ила из внешнего аппарата кратность разведения определяется по формуле:

D=

1 + R k + (1 + R )• t

где R – коэффициент

рециркуляции активного ила.

Коэффициент рециркуляции активного ила определяется дозой активного ила в поступающих сточных водах и дозой уплотненного активного ила во внешнем аппарате

R = X O

Xr - Xo где XO, XR – доза активного ила в потоке и во внешнем уплотнителе, из которого подают иловую смесь на рециркуляцию.

При отсутствии рециркуляции коэффициент рециркуляции и доза активного ила в потоке будут равны нулю. Первый член в правой части второго уравнения модели (7) возрастет по модулю и примет отрицательный знак, что приводит к увеличению скорости снижения дозы активного ила в системе. Вводя рециркуляцию, можно контролировать скорость снижения дозы активного ила, добиваясь более высоких скоростей и глубины очистки.

Доза активного ила в уплотненном состоянии определяется его иловым индексом по формуле XR

I

где I – иловый индекс, см3/г;

X R – доза уплотненного активного ила, г/л.

В общем случае при рециркуляции будет изменяться концентрация органических qR So + R ' SR загрязнений, поступающих в аппарат: SO = 1—r— , где S OR – концентрация органических загрязнений в поступающих на очистку сточных водах после смешения исходных сточных вод с подаваемой на рециркуляцию иловой смесью, в которой в общем случае могут быть остаточные органические загрязнения с концентрацией SR .

Удельная скорость окисления органических загрязнений описывается модифицированным уравнением кинетики ферментативных реакций типа Михаэлиса-Ментена [2; 3]:

p ( S,X,C l ) =p m '

___________ S ' C_L ___________

S ' C, + K_s ' C, + K_n ' C, L SL OL

'

1+ Ф' X

где p m - максимальная скорость окисления органических загрязнений, мг БПК/(г ила-ч);

K S – константа, характеризующая свойства органических загрязнений, мг/л;

К О – константа, характеризующая влияние кислорода, мг/л;

ф - коэффициент ингибирования процесса продуктами распада ила, л/г.

При численном моделировании были приняты3 коэффициенты уравнения (9), полученные для сточных вод городского типа, наиболее близкие по составу органических и прочих загрязнений хозбытовым сточным водам. Значения условно принимаются к расчету ввиду отсутствия подобных данных для сточных вод малых объектов водоотведения жилого сектора и сервиса (табл. 2.).

В фазе постоянного объема v=0 и D=0.

Поэтому модель (7) видоизменяется:

d-S =-p(S,X,Cl )■ X dt

dX dt

^YS ■p ( S,X,C_L ) ■ X - — ■ X

1000 ^L 24

}

Таблица 2.

Параметры расчетной модели (7) и (9)

	Параметр	Единица измерения	Значение
1.	Стехиометрический коэффициент прироста активного ила, Y S [1]	г ила/г БПК	0,45
2.	Коэффициент скорости самоочищения активного ила, b[1]	-1 сут	0,2
3.	Максимальная скорость окисления органических загрязнений, p m	мг/(г.ч)	85
4.	Константа, свойств органических загрязнений, K S	мг/л	33
5.	Константа, характеризующая влияние кислорода, К О	мг/л	0,625
6	Коэффициент ингибирования процесса продуктами распада ила, о	л/г	0,07