Исследования параметров гидроэнергетического потенциала Токтогульской ГЭС

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 621.22                                         

Вопрос энергосбережения является в настоящее время одной из наиболее актуальных проблем [1–4]. В работе проведены исследования взаимосвязи гидроэнергетических параметров гидроэнергетической станции с погодными изменениями природноклиматических факторов на территории гидрокаскадов и определения потенциала Токтогульского водохранилища КР [3–4]. Поскольку определение оптимальных параметров

cc) ® I работа ГЭС требуют знания гидроэнергетического потенциала реки Нарын с учетом расхода воды в Токтогульской ГЭС для различных целей.

Гидропотенциал Токтогульского ГЭС КР составим на основе модели водохранилища (Рисунок 1). Объем воды в водохранилище в момент времени t + At схематически можно представить:

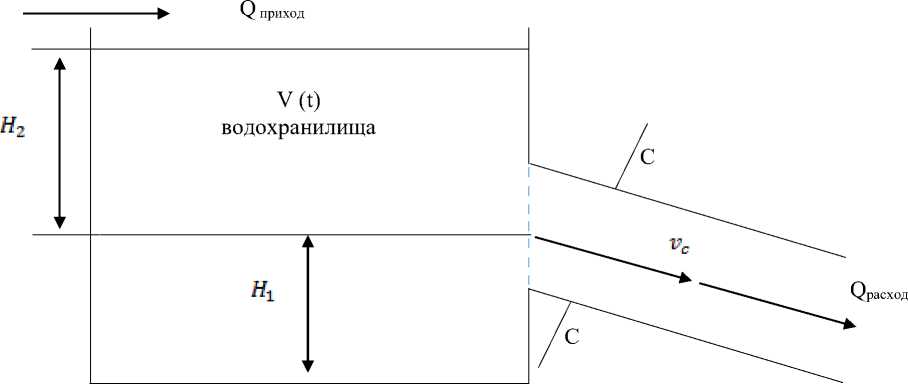
Рисунок 1. Схематическое изображение водохранилища: здесь V (t) — объем воды в водохранилище в момент времени t, м³, Q приход — приток воды в резервуар, м³/с. (объем воды, поступающей в водохранилище за время ∆t, м³/с), Q расход — отток воды из резервуара, м³/с

Ясно, что в процессе выработки электрической энергии в Токтогульской ГЭС уровень воды в водохранилище измениться.

Такое изменение уровня воды можно представить в виде следующих уравнений [3–4]:

Qnp - Q_BX + Q

□ СЕЩ

Qp« = Q отток

исп + ^переброс + Ффильтр

где Q вх — объем полезного стока, поступающий за время ∆t, м³/с; Q осад — объем воды, поступающий в водохранилище в виде осадков, м³/с; Q отток — отток воды из водохранилища за время ∆t, м³/с; Q исп — потери из-за испарения за время ∆t, м³/с; Q переброс — переброска части стока за время ∆t, м³/с; Q фильтр — фильтрационные потери из водохранилища за время ∆t, м³/с.

В работе моделирование стока с учетом внутригодового его распределения производилась по среднемесячному стоку. Таким образом, для плотинных ГЭС полезный сток воды практически пропущен через створ ГЭС. А потери расхода зависит от неэнергетических составляющих: Q исп , Q ф, Q осад, Q перебросил. Для:

^npiC^i)^* ⁼ K(O + Qep^i + Qocad^i ^— Qsux^i ^— Qucni^i ^— QnspsSi^i ^— Q^i^i , (3)

Без учета расхода на испарение, осадки и фильтрации через почвы из уравнения (3), опустив индекса получим:

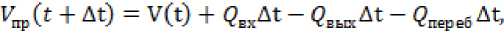
Откуда

Бюллетень науки и практики / Bulletin of Science and Practice Т. 7. №5. 2021 i^Ct+MMt) it

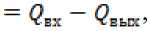
или

dv(t)    dv dt     dt

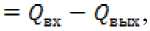
с другой стороны изменения уровня воды в процессе истечения воды можно представить в виде [4]:

H =H₂-H₁=^ + A^- здесь A = O,ll(-)⁰’²⁵ -5 2S                    d'

где a_c — коэффициент скорости ( a * 0,97), л — коэффициент местного сопротивления, учитывающий потери механической (кинетической и потенциальной) энергии воды.

Для ^Vc в сечении С-С имеет вид:

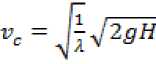
Скорость истечения воды из отверстия:

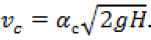
Расход воды, вытекающей через отверствия

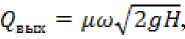
где № — коэффициент расхода: fi = sa , здесь £ — коэффициент сжатия водяной цилиндрической струи.

Для цлиндрического насадка коэффициент расхода   (№ )    принимает значения fl = 0,82 - 0,95, а коэффициент сжатия струи £ = 0,62 и a % 0,97, тогда

aca22gH a22gH

H = c c ° + A-^- = ahi + Aa2H 2g       2g

a^ + Aa2 - 1 = 0 так как Л = 0,11ф°'25 , тоa’ + 0,11ф°-25а2 -1 = 0. Тогда:

QBbK = Ha)V2gH = H^v'2g

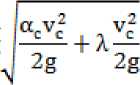
= цеп V acv2 + Av* = p.^vc

То есть Q_EbK = ^_с1ДГТа . Таким образом:

dv                 .------

^ = CEX - Щоус7ас+A

здесь to = ~- , поэтому Ц = 9BX - E«tTW + A. Поскольку для цилиндрической трубы £ « 0,62, то:

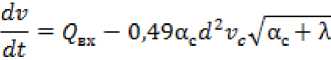
Или, окончательно получим выражение для изменения скорости истечения водяной

струи за определенный промежуток времени:

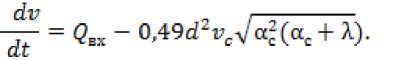
Таким образом, из формулы (14) видно, что изменения скорости истечения воды в водохранилище в первую очередь зависить от скорости истечения в сечениии С-С и от объема Фе к (объем притока воды). Чтобы сохранить необходимый объем воды в водохранилище, необходимо регулировать значения основных параметров (

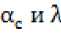
), входящий

во второй член данного уравнения, т. е. нужно оптимизировать значения этих параметров. путем их управления. Изменение объема воды в Токтогульском водохранилище в зависимости от времени показана на Рисунке 2.

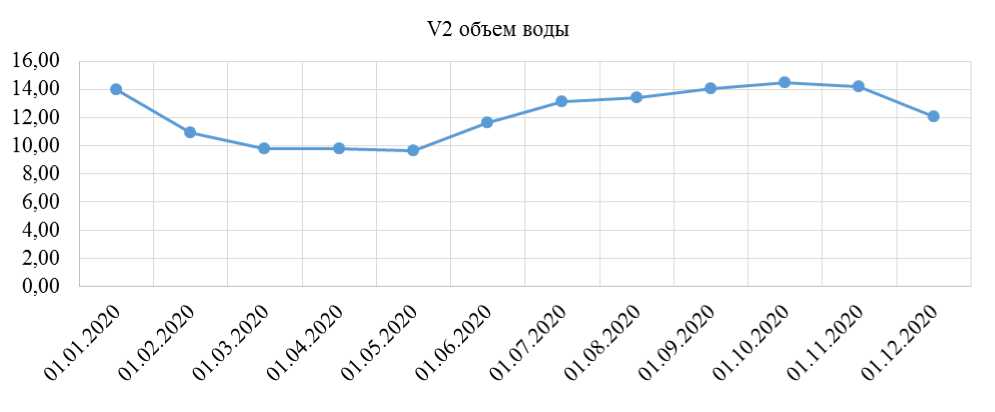
Рисунок 2. Изменения объема воды в Токтогульском водохранилище в зависимости от времени. Точки экспериментальные данные

Зависимость притока воды в Токтогульское водохранилище от времени представлена на Рисунке 3.

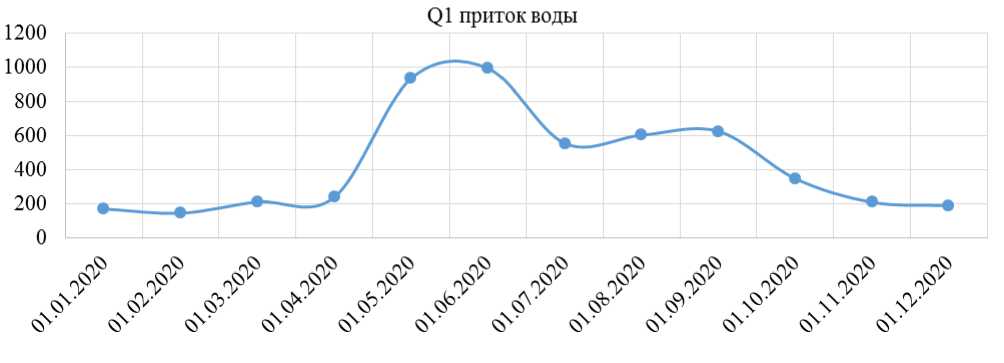
Рисунок 3. Приток воды в Токтогульское водохранилище

Из Рисунке 3 видно, что в 2020 г. максимальный приток воды приходиться на июнь-июль месяцы. В дальнейшем происходит резкое уменьшение притока воды. Нужно управлять параметрами входящие в формулу (14), чтобы правая часть полученной кривой зависимости, показанной на рисунке 3 плавно уменьшался.

На Рисунке 4 представлена зависимость расхода воды в Токтогульском водохранилище от времени. Из Рисунка 4 видно, что расход воды имеет два пика: в середине июля и второе увеличение расхода начинается с середины октября и быстрый подъем происходит начиная с середины ноября. Полученные данные можно объяснить тем, что увеличение расхода в июне и июля месяцы связаны с поливом, а увеличение расхода воды в ноябре и декабре месяцы связаны с увеличением потребности на электроэнергию.

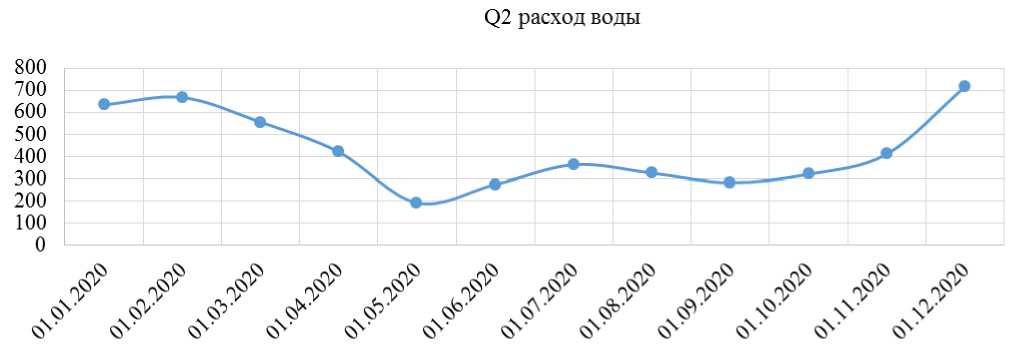
Рисунок 4. Зависимость расхода вода от времени года

В Таблице приведены обьем воды, имеющиеся на начало календарных месяцев 2020 г.

Таблица.

ОБЬЕМ ВОДЫ В ТОКТОГУЛЬСКОЕ ВОДОХРАНИЛИЩЕ в 2020 г, м3

14,954   13,589   12,474   11,647   11,650   12,646   13,482   14,028   14,864   15,201   14,819   13,748

Сравнивая результаты можно сделать вывод, что данные на 2020 г. приближаются к результатам расчетов [5]. Используя представленные данные в Таблице с применением метода наименьших квадратов нами получена следующее регрессионное уравнение [6]:

у = 12,66 + 0Д4х                                  (15)

Таким образом, на основе проведенных исследований, можно сделать вывод, что используя полученные уравнения (14) и (15) можно оптимизировать работу Токтогульской ГЭС, так как водосбережение в главном водохранилище КР, в настоящее время, является одним из эффективных способов решения вопроса устойчивого энергоснабжения населения и промышленных предприятий в КР.