Исследования процесса изменения фигур Хладни на колеблющейся мембране с тонким слоем жидкости

Фигуры Хладни, получаемые при помощи песка (или другого порошка), описывают узловые поверхности собственных колебаний плоских пластинок и мембран [1]. Если поместить частицу песка в какой-нибудь точке, не расположенной на узле, то при до статочно сильном поперечном колебании она будет двигаться (подпрыгивать и смещаться от первоначального положения). Движение частиц песка нерегулярно, но, после ряда прыжков, частица находит путь к узлу, как к единственному месту, где она может о статься в покое.

Известно, однако, что очень тонкий порошок, как, например ликоподий, ведёт себя отлично от песка. Вместо того чтобы собираться в узлах, он накапливается в местах максимального движения ‒ в пучностях [2]. В [3] была выдвинута гипотеза, что это явление может быть объяснено влиянием потоков воздуха, возникающих в результате колебания. В вакууме любой порошок всегда перемещается по направлению к узлам колеблющейся поверхности.

В настоящей работе проведено экспериментальное исследование фигур Хлад-ни, образующихся на поверхности круглой мембраны с нанесенным тонким слоем воды. Дана теоретическая интерпретация наблюдаемой трансформации песчаных фигур.

Экспериментальное исследование песчаных фигур на поверхности мембраны

Схема объекта исследования представлена на рис.1. Тонкая мембрана толщиной 7 ⋅10 ^{- 4} м служит дном массивной металлической чаши. Для обеспечения максимально жёсткой заделки мембраны по краю, мембрана и стенки чаши конструктивно выполнены единым элементом. Массивные стенки выполнены с таким расчётом, что при возбуждении собственных колебаний мембраны, амплитуда колебаний стенок чаши должна оставаться нулевой.

Рассматриваемая чаша же стко крепилась на металлическом столе интерферометра. Возбуждение производилось пьезокерамическим вибратором, подключенным к звуковому генератору. В первой серии экспериментов на предварительно обезжиренную мембрану насыпался мелкодисперсный песок. При подходе к резонансу мембраны песок начинал быстро перемещаться, концентрируясь в узловых линиях. На рис.2а представлен характерный вид расположения узловых линий (фигуры Хладни) на поверхности мембраны при различных резонансных частотах.

Во второй серии экспериментов с помощью песка регистрировались колебания мембраны с тонким слоем ( h _в ~ 10 ^{- 3} м)

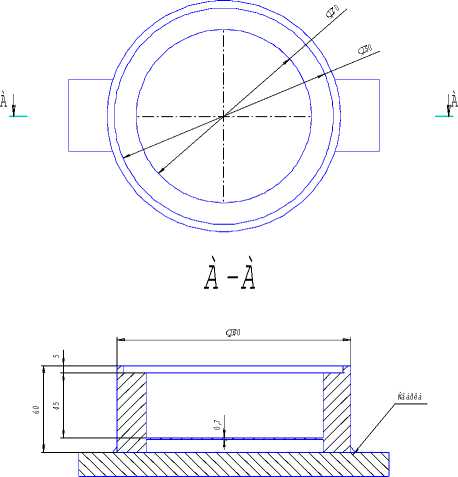
Рис.1. Схема объекта исследования воды. На рис.2 б представлены песчаные фигуры, наблюдаемые на поверхности мембраны для трех значений резонансных частот. С ростом частоты и амплитуды резонансных колебаний движение частиц к пучностям мембраны становилось более интенсивным. Очевидно, это явление аналогично, наблюдаемому в [2].

Потенциал радиационных сил, действующих на микрочастицы в жидком слое на поверхности колеблющейся мембраны

Для объяснения трансформации фигур Хладни в присутствии газо - жидко -стной среды рассмотрим сначала друго е известное явление -движение частиц суспензии в поле стоячей плоской волны. При этом частицы одних суспензий собирались в пучностях скорости, а других суспензий - в узлах скорости [4, 5]. Движение этих частиц связано с возникновением в стоячей плоской волне постоянной (не зависящей от времени) радиационной силы, действующей на частицы суспензии.

Если размеры частицы а <, где X -длина волны звука в жидкости, то радиационная сила имеет вид [4]

F = 4па2 E ka sin2 kh Ф(5, ц), (1)

где

Ф = 1 + 2(1 -5)/3 - 5 2+5      3ц2’ h- расстояние центра частицы от узла скорости, 5 = р0 / р*, ц = c* /c0, р0 и c0 - плотность и скорость звука в жидкой среде, р*

и c * - плотность и скорость звука в материале частицы, E -плотность энергии стоячих волн, k = 2 п / X .

Удвоенная пространственная периодично сть радиационной силы в стоячей волне (1) приводит к тому, что равновесным положением может быть либо узел, либо пучно сть, и маленькие частицы под действием этой силы собираются либо в узлах, либо в пучно стях стоячей волны. Как показывает анализ, при Ф >  0 (плотность частиц больше плотности среды) частицы собираются в пучно стях скорости, при Ф< 0 (плотность частиц меньше плотности среды) - в узлах скорости [4].

Очевидно, наблюдаемая трансформация фигур Хладни в газо-жидкостных средах также обусловлена воздействием радиационных сил. Выражение (1) справедливо только для плоских волн. Для произвольного акустического поля радиационные силы, действующие на маленькие частицы, могут быть определены через потенциал F = -V U , где потенциал U зависит от усреднённых по времени квадрата давления P и квадрата скорости среды в падающей звуковой волне [6]:

3 ,Р5, V!(1 -5).

U 2па р0[зр0c2(1 ца 2 + 5 L (2)

Таким образом, для объяснения трансформации фигур Хладни в жидком слое на мембране необходимо найти вид потенциала U. Для этого необходимо рассчитать характеристики акустического поля, возбуждаемого мембраной в слое воды, то есть распределение в этом слое давления и скорости в цилиндрической системе координат r, 0 ,z .

Без учёта присоединённой массы

2950 Гц                                    1800 Гц

3380 Гц

2040 Гц

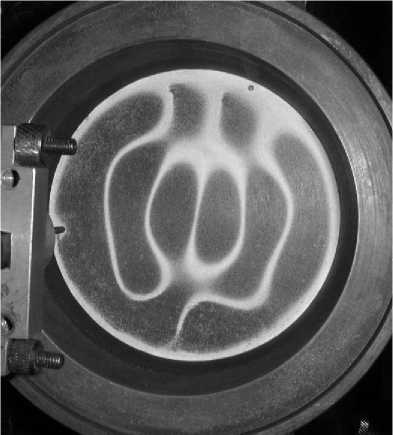
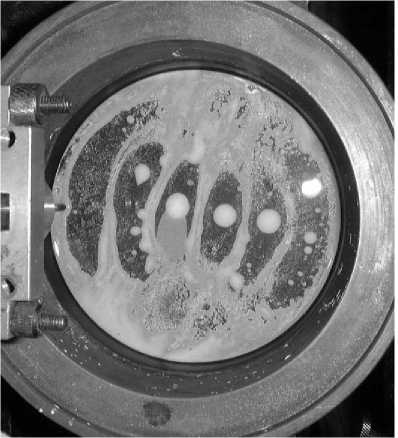
5780 Гц а)

5300 Гц б)

Рис.2. Характерный вид фигур Хладни на поверхности колеблющейся мембраны: а) без жидкости; б) с тонким слоем жидкости воды поперечное смещение круглой мембраны (её собственная мода) описывается формулой [7]

ξ = ξ ₀ J_n ( χ r ) cos n ( θ - α ) cos( ω t + ε ) , (3) где ξ ₀ - амплитуда смещения, J_n -функция Бесселя n порядка, ω = χ c -частота колебания, c = V T / ρ , T -натяжение мембраны, ρ - поверхностная плотность материала мембраны, α , ε -константы.

Величина χ определяется с помощью граничного условия. Когда закреплённая граница мембраны является окружностью радиуса r ₀ , имеем

Jn(χr0)=0.               (4)

Корни уравнения (4) определяют допустимые значения χ , а следовательно, и спектр собственных частот ω .

Система узлов, отображаемая фигурами Хладни, согласно (3) может быть разделена на две части: одну, состоящую из m концентрических окружностей, выражаемых уравнением

Jn(χr) = 0, и другую, со стоящую из n диаметров, расположенных равномерно вокруг центра,

θ =α+(2s +1) π

2 n где s целое число.

В частности, фигуры Хладни, приведенные на рис. 2 соответствуют собственным модам с n = 3, m = 1 и n = 1, m = 2

Определим теперь с помощью (3) и уравнений гидродинамики [8] акустическое поле мембраны вблизи поверхности пластинки ( z = 0 ). Имеем

∂ ξ

V =    = - ωξ ₀ J _n ( χ r ) cos n ( θ - α ) sin( ω t + ε ) ,

∂ t

P = -Ζωξ0Jn(χr)cosn(θ - α) cos(ωt +ε) ,

(6) где Ζ - акустиче ский импеданс, равный (в приближении бесконечной пластины) [9]

Ζ=

ρ 0 c 0

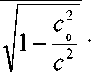
Откуда следует

U = -πa3ρ0ω2ξ02Jn2(χr)cos2 n(θ-α)× ×[(1-δ)+ (µ2-δ)c2 ]               . (8)

2+δ 3µ2(c02-c2)

В условиях эксперимента скорость звука в жидкости c0 превышает величину c, δ < 1 (плотно сть песка больше плотности воды), µ > 1 (скорость звука в песке больше скоро сти звука в воде), поэтому выражение в квадратных скобках положительно. В результате пучно сти движения мембраны соответствуют минимумам потенциала радиационных сил. В этих областях на частицы песка не действуют радиационные силы, причем положение покоя частиц устойчиво (механическая аналогия: частица на дне ямы). В узловых областях радиационные силы также равны нулю. Но эти области не устойчивы, так как соответствуют максимуму потенциала (механическая аналогия: частица на вершине холма). Радиационные силы приводят к движению частиц песка к областям максимального движения мембраны и препятствуют их стряхиванию в узловые области.

Заключение

Таким образом, наблюдаемая деформация фигур Хладни может быть связана с воздействием на частицы песка радиационных сил, возникающих в акустиче ском поле, создаваемом колеблющейся мембраной в жидкости. Эти силы противодействуют движению частиц к узлам. Амплитуда радиационных сил растёт пропорционально квадрату амплитуды колебаний мембраны, что приводит к наблюдаемому на эксперименте ускорению движения частиц к пучно стям колебаний мембраны.

Проведённый эксперимент свидетельствует также об инерционности установления поля радиационных сил (сначала на- блюдалось движение к узловым линиям, только затем ‒ к пучно стям). Выявление причин этой инерционно сти представляет интерес для дальнейших исследований. Важным моментом является также получение выявленного эффекта непосредственно в воздухе.