Исследования продольных колебаний ведущего участка гусеничной цепи с резинометаллическими шарнирными соединениями

Результаты теоретических и экспериментальных исследований показывают, что ведущий участок гусеничного обвода является самым нагруженным [1-5], его детали испытывают основную часть растягивающих усилий (рис. 1).

Рис. 1. Ведущий участок гусеничного движителя

Кроме того, велика доля вибрационных и ударных нагрузок, обусловленных пульсацией крутящего момента на ведущем колесе, цикличным ударным взаимодействием траков с зубьями ведущего колеса. Особенностью работы ведущего участка гусеничной цепи является изменение количества «свободных» звеньев по длине ведущего участка, т.е. звеньев, имеющих только

силовые связи (кинематические связи отсутствуют). Это явление в значительной степени зависит от жесткостных характеристик резинометаллического шарнирного соединения.

Одним из наиболее важных показателей, который позволяет оценить динамические параметры системы, является амплитудно-частотная характеристика (АЧХ). В работе [6] приводятся результаты экспериментальных исследований колебательных процессов в гусеничном обводе. Для проведении эксперимента использовался стенд, схема которого показана на рис. 2. В результате стендовых испытаний получены значения резонансных частот для различных участков гусеничного движителя, в том числе для ведущего. Однако экспериментальное определение амплитудно-частотных характеристик сопряжено со значительными трудностями. В связи с этим возрастает роль численных экспериментов при определении параметров колебательных систем.

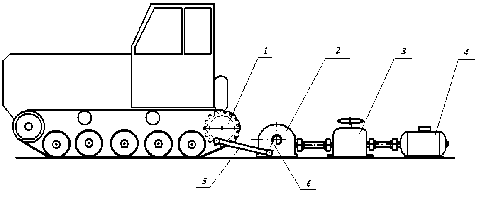
Рис. 2. Стенд для экспериментальных исследований колебательных процессов в гусеничном движителе:

1 – ведущее колесо; 2 – двухступенчатый редуктор; 3 – вариатор; 4 – электродвигатель; 5 – шатун; 6 – кривошип

В настоящей работе предлагается математическая модель гусеничного движителя, на основе которой проводятся теоретические исследования продольных колебаний. Расчетная кинематическая схема ведущего участка, представленная на рис. 3, включает четыре звена (элементы 1, 3, 5, 7), 4 резинометаллических шарнира элементы (элементы 2, 4, 6, 8) и ведущее колесо (элемент 9). Резинометаллический шарнир рассмотрен в виде отдельной массы, связанной с сопрягаемыми звеньями (i-1 и i+1 элементы) упругими и демпфирующими связями (рис. 3).

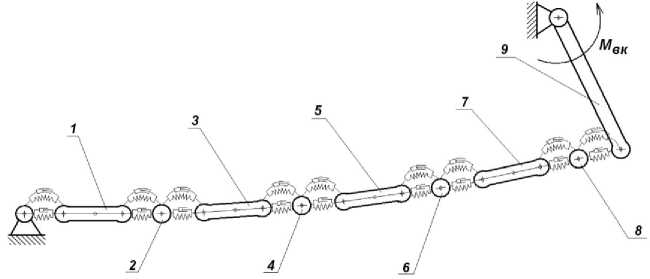
Рис. 3. Плоская модель ведущего участка гусеничного движителя:

1, 3, 5, 7 - звенья цепи; 2, 4, 6, 8 - шарниры; 9 - ведущее колесо (звездочка)

Жесткостные и демпфирующие параметры резиновых элементов двойных и тройных проушин характеризуются коэффициентами радиальной и угловой жесткости ( K 1 , K 2 , К _{ф 1} и К _{ф 2} ), а также коэффициентами радиального и углового демпфирования ( С 1 , С₂ , С _{ф 1} и С _{ф 2} ). Инерционные параметры элементов характеризуются массой и моментом инерции звеньев и шарниров ( m , J) и массой т вк и моментом инерции J_BK ведущего колеса. Положение каждого i - го элемента в глобальной системе координат XOY описывается координатами центра масс ( x i , y i ) и углом поворота локальной системы координат ( ^ i O i n i ) относительно глобальной системы координат - ф _г -.

Основные соотношения, описывающие динамическое поведение данной расчетной схемы рассмотрены в работе [7]. Математическая модель выражается системой нелинейных дифференциальных уравнений

[ м ] { q } + [ с {■ ( q ) } + [ K ] f ( q ) } = { p ( t ) } .

В соотношениях (1) [М], [С], [К] представляют собой соответственно матрицы масс, демпфирования и жесткости, а {P(t)} - есть вектор внешнего воздействия размерностью 3n, являющийся функцией времени. Решая систему дифференциальных уравнений методом временных конечных элементов [8], получаем значения линейных и угловых перемещений на каждом шаге исследуемого динамического процесса. Для теоретических исследований колебательных про- цессов в гусеничном движителе разработан программный комплекс DTRAK [9].

При проведении расчетов амплитудночастотных характеристик рассматриваемой динамической системы в качестве источника внешнего возмущения принимается гармоническое воздействие. Учитывался нелинейный характер изменения радиальной и угловой жесткостей шарнирного соединения (рис. 4, 5). На рис. 6 показана расчетная АЧХ для 5-го звена ведущего участка (продольные перемещения). Для сравнения на рисунке приводится экспериментальная АЧХ, полученная по результатам стендовых испытаний.

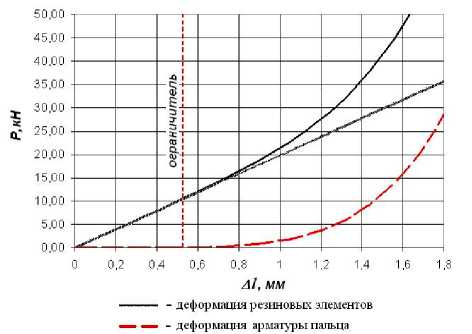
। 'и - суммарная жесткостная характеристика

Рис. 4. Компоненты жесткостной характеристики резинометаллического шарнира с ограничителями радиальных перемещений

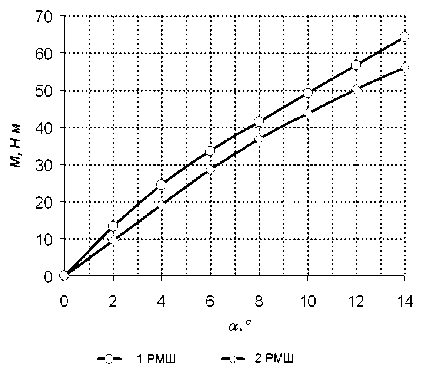
Рис. 5. Угловая жесткостная характеристика резинометаллического шарнира

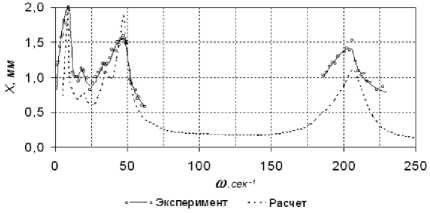
Рис. 6. Амплитудно-частотные характеристики для 4-го звена (горизонтальные перемещения)

В результате анализа амплитудночастотной характеристики на исследуемом частотном интервале выявлены следующие резонансные частоты: №1= 9 сек-1, м2 20 сек-1, №3=35 сек-1, №4=41 сек-1, №5= 207 сек-1. Сравнение расчетных и экспериментальных данных показывает, что расхождения в определении резонансных зон расчетной и экспериментальной АЧХ составляют не более 1-3 сек-1. Это можно объяснить нелинейностью системы, неидеальным синусоидальным воздействием, формируемым в результате проведения эксперимента и тем, что при расчете не учтены демпфирование и предварительное натяжение гусениц.