Исследования существующих требований собственника защищаемых информационных ресурсов на примере государственных органов

109004 Москва, ул. Б. Коммунистическая, д. 27, офис 335 Телефакс: (7 495)912-57-18, 103-04-49 E-mail:

СЕТЕВАЯ ВЕРСИЯ

ИНТЕЛЛЕКТУАЛЬНОГО БЛОКИРАТОРА СОТОВОЙ СВЯЗИ

«ИМБИРЬ»

«ИМБИРЬ-С», модель с ненаправленными антеннами внутри корпуса

Инженерно-производственным предприятием «НЕРА-С» завершена работа по созданию сетевой версии интеллектуального мультистандартного блокиратора сотовой телефонии «ИМБИРЬ-С», предназначенного для мониторинга и избирательного блокирования сото- вой связи стандартов GSM-900/1800, CDMA 450, IMT-MC-450 в группе помещений с управлением через сетевой интерфейс. При этом распределенные системы могут строиться как с использованием проводного интерфейса (отдельная сеть либо подключение к существу- ющей сети), так и радиоканала (ZigBee).

«ИМБИРЬ-С» отличает простота и технологичность конструкции, а также использование модульной системы, что дает возможность сконфигурировать каждое конкретное устройство под конкретные задачи. В зависимости от конфигурации помещений и других факторов возможно оснащение исполнительных устройств направленными антеннами разного типа, которые позволяют при значительном снижении мощности излучения четко локализовать воздействие блокиратора на мобильные телефоны исключительно внутри установленных зон.

Наряду с установкой в защищаемых помещениях сетевых устройств, объединяющих приемник и передатчик в одном корпусе, предусмотрен вариант разнесения функций приемника и блокиратора, что также обеспечивает повышение избирательности мониторинга и эффективности блокирования.

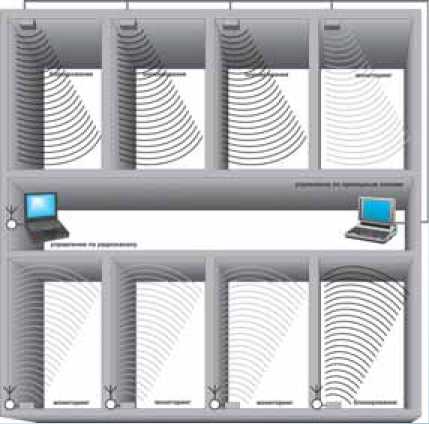
Примерная схема защиты нескольких помещений с использованием сетевого интерфейса

принимаемых на службу сотрудников, является уровень денежного довольствия, хотя сила зависимости свидетельствует о наличии и других факторов, влияющих на данный процесс.

Применяя метод наименьших квадратов, можно записать уравнение линейной регрессии для показателей «осуждено сотрудников в отчетном периоде в расчете на 1000 человек» и «отношение денежного довольствия сотрудников к средней начисленной заработной плате по стране» следующем виде:

у = -0,242 • х + 0,268

где в качестве зависимой величины выступает показатель «осуждено сотрудников в отчетном периоде в расчете на 1000 человек», а в качестве переменной – показатель «отношение денежного довольствия сотрудников к средней начисленной заработной плате по стране».

Коэффициент детерминированности для данной модели достаточно мал и составляет 0,32, то есть однофакторная модель не имеет достаточной корреляции с эмпирическими данными. Однако интерпретация даже такого упрощенного уравнения показывает, что даже при денежном довольствии сотрудников, находящемся на уровне средней начисленной заработной платы по стране (положим их отношение равным «1»), мы будем иметь остаточный уровень преступности среди сотрудников величиной 0,026 преступлений в расчете на 1000 человек личного состава, что соответствует примерно 7 преступлениям в год, при этом качество модели таково, что мы можем с высокой долей вероятности утверждать, что в указанном нами случае (при денежном довольствии сотрудников, находящемся на уровне средней начисленной заработной платы по стране), количество осужденных сотрудников не должно превысить 20 человек в год.

Из этого уравнения также видно, что только увеличение величины денежного довольствия сотрудников позволит существенным образом ужесточить критерии отбора на службу и, как следствие, понизить число осужденных сотрудников, хотя, как мы видим, денежное довольствие является не единственным и далеко не определяющим фактором в данном вопросе. В целом для продолжения исследования мы получили 8-факторную модель, которая даже в случае использования полинома второй степени будет очень затруднительна для интерпретации. В связи с этим, по всей видимости, нам следует использовать полином первой степени.

Перед построением общего вида модели построим еще одну однофакторную модель для фактора, имеющего одну из наибольших корреляций с показателем «осуждено сотрудников в отчетном периоде в расчете на 1000 человек» – «количество сотрудников, имеющих стаж службы от 3 лет до 10 лет».

Для этого случая уравнение будет иметь вид:

у =-0,00000295-х +0,438

Следовательно, мы для понижения уровня осужденных сотрудников должны наращивать ядро сотрудников со стажем от 3 до 10 лет до величины в 150 – 180 тысяч человек, хотя и в этом случае коэффициент детерминированности для данной модели достаточно мал и составляет 0,31.

Исходя из предварительных соображений следует ожидать, что использование 8-факторной модели увеличит ко- эффициент детерминированности до приемлемого уровня (хотя бы до 0,7 - 0,8). Следует учесть, что изначально мы не исследовали все факторы, влияющие на величину зависимого показателя (полная группа событий не составлялась), а некоторые из используемых нами факторов вполне могут оказаться «зашумляющими» модель.

При построении модели мы, исходя из некоторых технических аспектов, везде были вынуждены перейти к относительным величинам. Кроме того, вынужденно была исключена из рассмотрения величина показателя «количество сотрудников со средним общим образованием», поскольку она вошла в итоговое уравнение с коэффициентом «0».

Уравнение полученной 7-факторной модели имеет следующий вид:

у = -0,0587-х, -1,3912-х, -2,4829-х3 -1,384-х4 --1,496-х5 -0,2645-х6 +1,298-х7 +2,4495

^, при этом коэффициент детерминированности равен 1, а ошибки входящих в модель коэффициентов отсутствуют до 4-го знака включительно (!).

Факторы в уравнении следуют в следующем порядке:

• ♦    отношение денежного довольствия сотрудников к средней начисленной заработной плате по стране – x₁ ;

• ♦    работает женщин в расчете на число сотрудников (фактически) – x₂ ;

• ♦    количество сотрудников в возрасте до 30 лет в расчете на число сотрудников (фактически) – x₃ ;

• ♦    количество сотрудников, имеющих стаж службы от 1 года до 3 лет, в расчете на число сотрудников (фактически) – x₄ ;

• ♦    количество сотрудников, имеющих стаж службы от 3 до

• 10 лет, в расчете на число сотрудников (фактически) – x₅ ;

• ♦    количество сотрудников, принятых за отчетный период, в расчете на число сотрудников (фактически) – x₆ ;

• ♦    количество сотрудников, уволенных за отчетный период, в расчете на число сотрудников (фактически) – x₇ .

• ♦    В качестве зависимой величины ( y ) выступает показатель «осуждено сотрудников в отчетном периоде в расчете на 1000 человек».

Общий вид уравнения позволяет судить о том, что 6 переменных входят в уравнение с отрицательными знаками (то есть их рост приводит к снижению уровня осужденных сотрудников) и лишь одна переменная и свободный член имеют тенденцию к росту (положительные величины).

Исходя из направленности связей по отдельным факторам ожидалось вхождение всех факторов в модель с отрицательными знаками, однако показатель «количество сотрудников, уволенных за отчетный период, в расчете на число сотрудников (фактически)» – x₇ вошел в модель с положительным знаком, что может быть обусловлено косвенной взаимосвязью указанного показателя с другими объясняющими факторами, вошедшими в модель.

Наибольший вклад в модель дает такой фактор, как «количество сотрудников в возрасте до 30 лет в расчете на число сотрудников (фактически)», на втором месте находится такой фактор, как «количество сотрудников, имеющих стаж службы от 3 до 10 лет, в расчете на число сотрудников (фактически)». Уже варьирование до уровня 0,5 от фактического числа сотрудников первого показателя (x1)по ре- зультатам модели позволяет снизить уровень осужденных сотрудников практически до нуля.

В связи с вышесказанным следует, что используемая модель очень чувствительна к изменению одного из параметров (иными словами, даже варьирование этого показателя до уровня 0,8 – 0,9 не должно было приводить к такому значительному изменению результирующего фактора). Вместе с тем модель не надежна с точки зрения скейлинга (или теории размерности) - устремление значащих факторов к экстремальным значениям приводит к недостоверным результатам. В связи с этим мы попытаемся видоизменить модель, избавившись от свободного члена.

Новое уравнение будет выглядеть следующим образом:

у = -0,2683 • X, - 0,1942 • х2 +11,2796 • х3 - 7,33196 • х4 -- 3,91997 • х, +1,28754 • х, - 4,42703 • х7 - 2,09692 • х„

• ■                       J *                       О *                       /          *                       О .

В отличие от предыдущего, в него вошли все восемь факторов («количество сотрудников со средним общим образованием в расчете на число сотрудников (фактически)» – x₃ , остальные факторы те же), однако по факторам x₃ и x₆ мы наблюдаем изменение направленности связи по сравнению с ожидаемой. В свою очередь фактор x₈ изменил знак по сравнению с предыдущим уравнением.

Этап 2. Устранение мультиколлинеарности. Построение окончательной модели

Поскольку полученные результаты не удовлетворили нас, то следует понимать, что в анализе множественных корреляционных связей (так называют статистические связи между более чем двумя переменными в отличие от парных связей, рассмотренных выше) есть своя специфика и возникают принципиально новые проблемы. Эта специфика связана, прежде всего, с необходимостью измерять степень тесноты связи между результирующей величиной и множеством объясняющих переменных, а также возникающими трудностями в интерпретации парных коэффициентов корреляции, обусловленных возможным опосредованным влиянием на эту связь других объясняющих переменных.

Последнее обстоятельство делает необходимым введение таких измерителей статистической связи, которые были бы очищены от опосредованного влияния других переменных и давали бы оценку степени силы интересующей нас связи между величинами при условии, что значения всех остальных переменных зафиксированы на некотором постоянном уровне. В этом случае говорят о статистическом анализе частных (или «очищенных») связей и используют частные коэффициенты корреляции [7].

В частности, для двухфакторного случая имеем:

^01(2)

Г01   ^02^12

,

где: r₀₁ – парный коэффициент корреляции между зависимым фактором и первой переменной, r₀₂ – парный коэффициент корреляции между зависимым фактором и второй переменной, r₁₂ – парный коэффициент корреляции между первой и второй переменными.

Последовательно применяя к излишним переменным все новые признаки из рассматриваемого набора, можно получить рекуррентные соотношения для подсчета частных коэффициентов корреляции. Так, например, для случая трех факторов имеем

^01(2) ^{— Г}03(2)^Г13(2) o^Ja³^) ^.

01(3)

На практике возможен расчет частных коэффициентов корреляции лишь для двух факторных моделей, даже в случае трех влияющих факторов расчет частного коэффициента корреляции представляет значительную сложность.

Используя программное средство SPSS, вычисляем частную корреляцию между показателем «осуждено сотрудников в отчетном периоде в расчете на 1000 человек» и отношением «денежного довольствия сотрудников к средней начисленной заработной плате по стране». Получаем, что коэффициент корреляции составил минус 0,646, что существенно выше, чем в случае парной (не частной) корреляции.

Рассчитав частную корреляцию между указанными показателями при исключении показателей «работает женщин в расчете на число сотрудников (фактически)» – x₂ и «количество сотрудников, имеющих стаж службы от 1 года до 3 лет, в расчете на число сотрудников (фактически») – x₄ , мы получили частный коэффициент корреляции на уровне минус 0,807.

Последовательное исключение еще одного показателя – «количество сотрудников, имеющих стаж службы от 3 до 10 лет, в расчете на число сотрудников (фактически)» – x₅ – привело к изменению частного коэффициента корреляции до -0,829. Следующее исключение еще одного показателя «количество сотрудников, принятых за отчетный период, в расчете на число сотрудников (фактически)» – x₆ – также увеличило частный коэффициент корреляции до -0,850.

Перед построением многомерной регрессионной модели представляется целесообразным предварительно провести математико-статистический анализ взаимосвязи между переменными на наличие мультиколлинеарности, которая может привести к недостоверным оценкам модели. Данный ана-

Таблица 1

	х1	х2	х3	х4	х5	х6	х7	х8
х1	1	-0,33053	0,45105	0,47498	0,43934	-0,10669	0,42536	0,06832
х2	-0,33053	1	-0,94477	-0,92527	-0,83915	0,81842	-0,75081	-0,55937
х3	0,45105	-0,94477	1	0,96154	0,92514	-0,62320	0,88308	0,65764
х4	0,47498	-0,92527	0,96154	1	0,94406	-0,59040	0,74331	0,69132
х5	0,43934	-0,83915	0,92514	0,94406	1	-0,45198	0,72940	0,71812
х6	-0,10669	0,81842	-0,62320	-0,59040	-0,45198	1	-0,45054	-0,07249
х7	0,42536	-0,75081	0,88308	0,74331	0,72940	-0,45054	1	0,46186
х8	0,06832	-0,55937	0,65764	0,69132	0,71812	-0,07249	0,46186	1

Таблица 2. Сводка для модели(b)

R	R-квадрат	Скорректированный R-квадрат	Стандартная ошибка оценки
0,783(a)	0,614	0,324	0,03667

лиз может быть проведен по методу Феррара и Глобера [8] ^.

Косвенным подтверждением реальной (или частной) мультиколлинеарности является анализ матрицы парных коэффициентов корреляции. Было установлено, что показатель «работает женщин в расчете на число сотрудников (фактически)» имеет корреляцию с показателями «количество сотрудников со средним общим образованием в расчете на число сотрудников (фактически)», «количество сотрудников в возрасте до 30 лет в расчете на число сотрудников (фактически)», «количество сотрудников, имеющих стаж службы от 1 года до 3 лет, в расчете на число сотрудников (фактически)», «количество сотрудников, имеющих стаж службы от 3 до 10 лет, в расчете на число сотрудников (фактически)», «количество сотрудников, принятых за отчетный период, в расчете на число сотрудников (фактически)» на уровнях: -0,944767181, -0,925271082, -0,83915326, 0,818418404, -0,75080952 соответственно.

Помимо этого, обнаружены высокие коэффициенты корреляции показателя «количество сотрудников со средним общим образованием в расчете на число сотрудников (фактически)» с показателями «количество сотрудников в возрасте до 30 лет в расчете на число сотрудников (фактически)», «количество сотрудников, имеющих стаж службы от 1 года до 3 лет, в расчете на число сотрудников (фактически)», «количество сотрудников, принятых за отчетный период, в расчете на число сотрудников (фактически)» на уровнях: 0,961544497, 0,925135012, 0,88308262 соответственно.

Показатели «количество сотрудников в возрасте до 30 лет в расчете на число сотрудников (фактически)» и «количество сотрудников, имеющих стаж службы от 1 года до 3 лет, в расчете на число сотрудников (фактически)» коррелируют на уровне 0,944058779.

Считается, что наличие значений коэффициентов корреляции по абсолютной величине превосходящих 0,75 – 0,8 свидетельствует о присутствии мультиколлинеарности [7]. О присутствии явления мультиколлинеарности сигнализируют и некоторые внешние признаки модели, построенной нами на первом этапе:

• ♦    некоторые из факторов имеют неправильные с точки зрения практической работы знаки и не оправданно большие значения;

• ♦    небольшое изменение исходных статистических данных

приводит к существенной нестабильности результирующего значения;

• ♦    большинство или даже все оценки коэффициентов регрессии оказываются статистически не значимыми, а модель в целом является статистически значимой.

В табл. 1 приведена матрица парных коэффициентов корреляции.

Для полного понимания значимости факторов, входящих в модель, было бы целесообразно построить матрицу частных парных коэффициентов корреляции, но вычисление их более трудоемко, как указывалось ранее.

Для борьбы с явлением мультиколлинеарности и его последствиями на практике используют следующие подходы:

преобразуют факторы в новые переменные, уменьшая тем самым количество переменных (чисто технически мы использовали этот способ, перейдя к новым переменным в расчете на число сотрудников (фактически), однако в данном случае надо понимать, что речь идет о более серьезных преобразованиях (факторный анализ));

• ♦    используют методы регуляризации (например, гребневой регрессии, стабилизирующих оценок или «сжатых» оценок [9]);

• ♦    исключают из совокупности факторов одну или же несколько линейно связанных факторных переменных, чтобы вновь полученные элементы корреляционный матрицы были меньше порогового значения 0,8.

Каждый из этих подходов обладает очень серьезными недостатками, которые снижают эффективность их применения [10].

Исходя из вышеизложенного в качестве критерия отбора входящих в модель факторов мы выбрали максимизацию частных парных корреляций факторов, входящих в модель.

Таким образом, в модель целесообразно включить следующие факторы:

• ♦    отношение денежного довольствия сотрудников к средней начисленной заработной плате по стране – x₁ ;

• ♦    количество сотрудников, уволенных за отчетный период в расчете на число сотрудников фактически – x₂ ,

• ♦ нагрузка на одного сотрудника — х₃ .

В качестве зависимой величины ( y ) выступает показатель «осуждено сотрудников в отчетном периоде в расчете на 1000 человек». Уравнение полученной 3-факторной модели имеет следующий вид:

.

Указанная модель является достаточно грубой (коэффициент детерминированности составляет 0,61, при этом она имеет достаточно существенные стандартные ошибки ко-

Таблица 3. Коэффициенты (a)

Наименования	Нестандартизованные коэффициенты		Стандартизованные коэффициенты β	t	Значения поправочных коэффициентов	Корреляции
переменных	a	Стандартная ошибка				Нулевой порядок	Частные	Частичные
Константа	0,199	0,151		1,321	0,257
Отношение	-0,265	0,135	-0,616	-1,963	0,121	-0,563	-0,700	-0,610
Уволено	-0,964	0,925	-0,338	-1,043	0,356	-0,226	-0,462	-0,324
Нагрузка	0,053	0,032	0,538	1,646	0,175	0,354	0,636	0,511

эффициентов и константы), но при всех своих неточностях достаточно хорошо применима в целях подтверждения поведения моделируемой переменной от зависимых факторов.

Иными словами, управляющее воздействие может быть выражено в повышении заработной платы до уровня в 1,2 от средней начисленной заработной платы по стране, в ежегодном увольнении 21 % процента личного состава или в снижении нагрузки на одного работающего до уровня в 1,1 осужденного на одного человека личного состава. При выполнении любого из указанных условий преступность личного состава практически иллиминируется до уровня в 5 – 7 осужденных сотрудников в год.

Характеристики модели и полученных коэффициентов приведены в табл. 2, 3.

a - предикторы: «константа», «нагрузка», «отношение», «уволено»;

b - зависимая переменная «осуждено сотрудников».

Коэффициент корреляции показывает, что зависимая переменная и оптимальная линейная комбинация независимых переменных имеют достаточно высокую корреляцию. Однако «скорректированный R -квадрат» достаточно мал и существенно различается от значения величины « R -квадрат». По всей видимости, в этом случае следует больше доверять величине «скорректированный R -квадрат», которая ставит под сомнение надежность модели. Однако стандартная ошибка оценки не велика и не сильно отличается от нуля (если прямая линия точно подгоняет данные, то стандартная ошибка оценки равна нулю ⁾ .Уровень значимости F -критерия составляет 0,24 и говорит о наличии нелинейной составляющей, не учтенной моделью. F -статистика используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет. Величина F может сравниваться с критическими значениями в публикуемых таблицах F -распределения может быть использована для вычисления возможности получения наибольшего значения F .

a - зависимая переменная «Осуждено сотрудников»

Полученные нам коэффициенты позволяют проводить экстраполяцию модели в достаточно широких интервалах без потери смысла получаемых данных и устойчивости уравнения. Однако стандартные ошибки коэффициентов достаточно велики, что также свидетельствует о невысоком качестве модели. β-коэффициенты позволяют судить, что по степени важности влияния параметры подразделяются следующим образом:

• ♦    на первом месте по степени важности или по величине воздействия на изменяемую величину находится величина денежного довольствия личного состава (отношение денежного довольствия сотрудников к начисленной заработной плате по стране);

• ♦    на втором месте - нагрузка на одного сотрудника;

• ♦    на третьем месте - количество сотрудников, уволенных за отчетный период в расчете на число сотрудников фактически.

Значимость t -критерия оказывается неудовлетворительной. Наилучшую значимость мы имеем для показателя «отношение денежного довольствия сотрудников к средней начисленной заработной плате по стране», иными словами, для этого фактора мы имеем объяснение более 80% входящих в модель точек, однако другие факторы существенно огрубляют модель, либо имеют нелинейную зависимость. Еще одним параметром, существенно влияющим на качество модели, является количество используемых данных, которое в нашем случае невелико. В плане повышения качества модели возможен еще целый ряд шагов, которые способны существенно улучшить полученные результаты (проведение дисперсионного анализа по видам подразделений и моделирование данных по отдельному виду; устранение искажений внесенных отдельными подразделениями и территориальными органами (предварительный анализ данных); использование методов факторного анализа на этапе устранения мультиколлинеарности и т.п.).

Таким образом, повышая требования к технической составляющей защиты информации и тем самым завышая квалификационные требования к сотрудникам подразделения по технической защите информации без соответствующей их мотивации, можем получить обратный результат (видимо следует расширить данный абзац и оценить разницу в оплате сотрудников подразделений по защите информации и обычных подразделений, а затем ввести ее в модель и показать, что разница в указанных значениях очень незначительна).

Изложенное выше позволяет сделать вывод о том, что при выборе средств защиты информации необходимо исходить из экономической целесообразности, включающей в себя временную актуальность и требования к персоналу с точки зрения обслуживания применяемых средств защиты.