Исследования в области электрофизики, основанные на теореме Лапласа и физических информационных нейронных сетях

Теорема Лапласа – одно из фундаментальных дифференциальных уравнений, описывающих стационарные физические явления в виде: v ² p = о .

где p - скалярное поле (например, электрический потенциал, температурное поле и т. д.). Теорема имеет важные приложения в области электрофизики, теплопроводности, гидродинамики и т.д.

Физические нейронные сети – это новый метод моделирования и решения физических явлений в непрерывном пространстве путем встраивания решений и граничных условий дифференциальных уравнений в модели глубокого обучения. Этот подход демонстрирует значительные преимущества при решении высокоразмерных сложных систем.

Целью данной работы является изучение процесса моделирования и решения задач стационарного состояния в электрофизике пу- тем объединения теоремы Лапласа с PINN. Сначала мы представим основы PINN, а затем проверим метод на примере двумерной задачи о распределении потенциала.

• 1.    Теоретическая база

  • 1.1.    Теорема Лапласа

Теорема Лапласа описывает поведение распределения скалярного поля в пассивной области: v ² p = 0

В декартовой системе координат уравнение Лапласа выражается как V2p = дp / дx2 + d2p / ду2 + дp / дz2 = 0, где p может обозначать электрический потенциал. Это уравнение показывает, что потенциал удовлетворяет частному дифференциальному уравнению второго порядка, когда в пространстве нет распределения чистого заряда. В физическом смысле, в области без источника заряда распределение потенциала является гладким и не меняется резко из-за наличия локализованного заряда.

Возьмем, к примеру, вывод уравнения Лапласа из фундаментального уравнения электростатического поля в декартовой системе координат. Согласно закону Гаусса v - E = p / s₀ , в области отсутствия распределения заряда p = 0 и напряженности электрического поля E =-∇ ϕ , замена E = -∇ ϕ на v- E = 0 , т.е. v- ( -v p ) = 0 , дает v V = 0 .

• 1.2.    Принципы физических нейронных сетей (PINN)

  • 1.2.1.    Архитектура и механизм работы PINN

Анализируется иерархия сети PINN, включая настройку входного, скрытого и выходного слоев. На входной слой поступают независимые переменные физической задачи, такие как пространственные координаты, время и т.д.; скрытый слой выполняет извлечение признаков и отображение входной информации посредством нелинейных преобразований между нейронами; а выходной слой выдает решение задачи, такое как физические величины электрического потенциала и напряженности электрического поля. Объясните подробно, как законы физики включаются в процесс обучения нейронной сети в виде функций потерь или ограничений.PINN формирует следующую оптимизационную задачу, вводя законы физики (например, дифференциальные уравнения, начальные краевые условия) непосредственно в функцию потерь нейронной сети: L =αL +βL . Где Lpde – остаток дифференциального уравнения [1], который получается путем подстановки решения, предсказанного нейронной сетью, в дифференциальное уравнение и вычисления разности между левой и правой частями уравнения, а L – отклонение от граничных условий, которое сравнивает предсказанное нейронной сетью значение на границе с известным значением граничных условий. α и β – весовые коэффициенты, которые используются для настройки относительной важности ограничений дифференциального уравнения и ограничений граничных условий в функции потерь [2]. Оптимизируя параметры нейронной сети, PINN может получать приближенные решения, обеспечивая при этом физическую согласованность. В процессе обучения оптимизационные алгоритмы, такие как стохастический градиентный спуск, обычно используются для непрерывной настройки весов и смещений нейронной сети с целью минимизации функции потерь, чтобы выход нейронной сети максимально удовлетворял физическим законам и граничным условиям.

• 1.2.2.    Различия и преимущества по сравнению с традиционными нейронными сетями

Сравнение традиционных нейронных сетей по степени зависимости от данных, способности к обобщению и пониманию природы физики с PINN подчеркивает значительные преимущества PINN в решении задач, обусловленных физикой. Традиционные нейронные сети в основном полагаются на большой объем обучающих данных для изучения взаимосвязи между входами и выходами, в то время как PINN не только использует данные, но и включает физические знания, и хорошо работает с ограниченными данными; с точки зрения способности к обобщению, PINN обладает лучшей способностью предсказания для невидимых данных благодаря ограничениям, накладываемым законами физики; и с точки зрения понимания природы физики, PINN может более точно отражать внутренние законы физических процессов, в то время как традиционные нейронные сети могут лишь поверхностно соответствовать данным [3-5].

• 1.3.    Комбинированный подход с использованием теоремы Лапласа и PINN

  • 1.3.1.    Построение функции потерь на основе уравнения Лапласа

Подробное описание того, как уравнение Лапласа может быть дискретизировано и преобразовано в штрафной член для функции потерь PINN, путем корректировки весов для баланса соответствия данных и степени удовлетворения физических ограничений. Уравнение Лапласа пространственно дискретизируется, например, с помощью методов конечных разностей, конечных элементов и т.д., в набор алгебраических уравнений. Эти дискретизированные уравнения затем добавляются к функции потерь PINN в виде членов L , а вклад ограничений уравнения Лапласа во всю функцию потерь регулируется путем настройки весовα , чтобы модель соответствовала данным и удовлетворяла физиче- ским законам, описываемым уравнением Лапласа.

• 1.3.2.    Способы введения физических ограничений, связанных с Лапласом, в PINN

• 2.    Экспериментальный пример – решение распределения поля параллельного пластинчатого конденсатора

  • 2.1.    Описание проблемы и физическое моделирование

• 2.2.    Теоретический анализ на основе теоремы Лапласа

• 2.3.    Построение и обучение модели PINN2.3.1.    Структура сети

• 2.3.2.    Учебные данные

• 2.3.3.    Функция потерь

• 2.3.4.    Параметры обучения и оптимизатор

  С помощью оптимизатора Adam начальная скорость обучения была установлена на 0,001. С помощью планировщика скорости обучения скорость обучения умножалась на 0,1 каждые 1000 циклов обучения, в общей сложности 5000 циклов обучения.

• 2.4.    Сравнение и анализ результатов

Изучить конкретные способы включения граничных условий, связанных с теоремой Лапласа (например, граничных условий Дирихле, граничных условий Неймана), закона сохранения энергии, закона сохранения заряда и т.д., в процесс обучения и прогнозирования PINN в виде мягких или жестких ограничений. Для граничных условий Дирихле (известные значения функции на границе) разница между предсказанными и известными значениями на границе может непосредственно использоваться как часть члена L ; для граничных условий Неймана (известные значения нормальной производной функции на границе) соответствующий член потерь получается путем вычисления нормальных производных предсказанных нейросетью значений на границе и сравнения их с известными значениями. Для законов сохранения энергии и заряда ограничения могут быть реализованы путем добавления остаточных членов соответствующих сохраняемых величин к функции потерь или путем явного ограничения вычислительного процесса нейронной сети, чтобы гарантировать, что модель следует этим физическим законам во время обучения и прогнозирования [6].

Представлены структурные параметры параллельно-пластинчатого конденсатора, в котором расстояние между полюсами и пластинами равно L = 1.0, а приложенное напряжение равно    V = 1.0, пренебрегая краевым эффектом [7]. Предполагая, что площадь полюсных пластин пока явно не задана, создается одномерная модель распределения электрического поля, в которой одна из полюсных пластин является началом координат, а перпендикулярное полюсной пластине направление – осью x. В качестве точек обучающей выборки равномерно выбирается N = 100 точек в интервале [0,L].

Внутри конденсатора без распределения заряда потенциал удовлетворяет уравнению Лапласа. В сочетании с граничными условиями (потенциал на одной полюсной пластине равен V = 1.0 , а на другой - 0 ) теоретическое распределение потенциала получается путем двойного интегрирования как ф ( x ) = V _o (1 - x / L ) , что, в свою очередь, дает напряженн сть электрического поля E ( x ) = V , / L , основанную на зависимости между напряженностью электрического поля и потенциалом [8].

Для определения структуры сети PINN входной слой представляет собой нейрон, соответствующий координате x, скрытый слой состоит из двух слоев, каждый слой содержит 20 нейронов, в качестве функции активации выбрана функция ReLU, а выходной слой представляет собой нейрон, выводящий потенциал.

В интервале [0,L] было сгенерировано N=100 равномерно распределенных обучающих точек, которые использовались для последующего обучения модели с выведенным набором атрибутов и размещались на соответствующем вычислительном устройстве в зависимости от устройства.

Построена функция потерь на основе уравнения Лапласа, состоящая из двух частей: потери PDE, которые получаются при вычислении производной второго порядка от прогноза потенциала, и потери граничных условий, которые вычисляются на основе разницы между прогнозом потенциала и теоретическим значением на границе. Общая потеря получается путем взвешенного суммирования потерь от PDE и потерь от граничных условий, а вес принимает значение 1.0.

Результаты распределения электрического поля, полученные с помощью PINN, сравниваются с теоретическим аналитическим решением. Результаты обучения сначала преобразуются из конкретного формата в форму массива, а одномерные результаты расширяются до двух измерений путем создания двумерной сетки. После этого строятся тепловая карта распределения потенциала и тепловая карта абсолютной ошибки, предсказанной PINN, и аннотируются путем добавления цветных полос, а затем изображения сохраняются. Результаты визуализации показывают, что PINN лучше отражает характеристики распределения потенциала, а его ошибка в основном сосредоточена в области, близкой к границе (рис.).

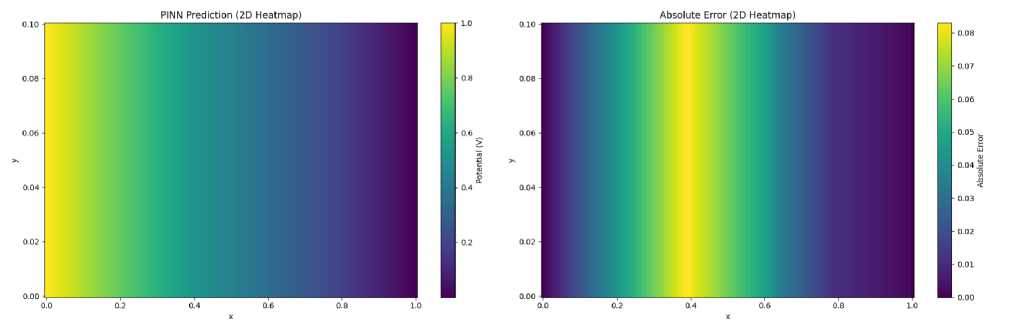
Рисунок.

Поскольку PINN учитывает физические законы (например, теорему Лапласа и другие соответствующие физические ограничения при решении электрофизических задач) в процессе построения, результаты прогнозирования не только хорошо согласуются с данными, но и удовлетворяют требованиям физических законов. Из идеальных результатов прогнозирования и низкой погрешности, представленных на рисунке, можно сделать вывод, что PINN с большей вероятностью дает обоснованные прогнозы, основанные на физической согласованности, и обладает лучшей способностью к обобщению, которую трудно сравнить с традиционными методами, управляемыми данными, даже когда приходится сталкиваться с ситуациями, не полностью охваченными обучающими данными [9, 10].

Заключение

Таким образом, в данном исследовании теорема Лапласа в электрофизике успешно сочетается с физической нейронной сетью (PINN) и применяется для решения задачи распределения электрического поля параллельных пластинчатых конденсаторов. Построив подходящую архитектуру модели PINN, тщательно разработав функцию потерь и разумно задав параметры обучения, мы эф- фективно используем ограниченные данные обучения и физические законы, вытекающие из теоремы Лапласа, и получаем более точное предсказание распределения электрического поля. Несмотря на то, что вблизи граничной области все еще остаются некоторые ошибки, данное исследование полностью демонстрирует большой потенциал PINN в решении задач электрофизики с устойчивым состоянием поля.

Будущие исследования могут продолжить изучение того, как оптимизировать модель PINN для повышения точности прогнозирования в более сложных условиях электрического поля, таких как наличие нескольких сред и неоднородных распределений заряда. В то же время ценно также исследовать, как более тесно интегрировать другие связанные законы физики с PINN, чтобы расширить ее применение в других областях электромагнетизма. Кроме того, глубокий анализ вычислительной эффективности и ресурсоемкости PINN при решении задач различного масштаба имеет большое значение для содействия применению этого метода в практической инженерии, что, как ожидается, принесет новые прорывы и возможности для исследований и практики электрофизики и смежных областей.