Итерационная модель упругого деформирования конгломерата частиц с учетом сжимаемости среды в процессе прессования

Финансирование. Исследование выполнено за счет гранта Российского научного фонда № 24-29-00089

Original Theoretical Research

Iterative Model of Elastic Deformation of a Particle Conglomerate Taking into Account the Compressibility of the Medium during Pressing

Ivan K. Andrianov ® H , Sergey N. Ivano v® , Elena K. Chepurnova

Komsomolsk-na-Amure State University, Komsomolsk-on-Amur, Russian Federation

Introduction . Briquetting and pressing of wood and other powdered materials are becoming key processes in the circular economy and recycling of wood processing waste. Accurate calculation of compaction pressure is essential for equipment selection and optimization, making the task of modeling the deformation of conglomerates both practical and economically significant. The literature addresses the mechanics of powder media, porous materials, and the modeling of elastic-plastic deformations of granular conglomerates. However, most models assume fixed mechanical characteristics or approximations that do not account for the dependence of strength and elastic properties on changing density under compression. This leaves a gap in theoretical and applied approaches to adequately calculating pressure for materials with variable density. Therefore, the objective of this work is to develop an approach for calculating the compaction pressure of a particle conglomerate as a function of the degree of elastic compression, taking into account changes in the mechanical characteristics of the medium.

Materials and Methods . In the mathematical description of the research problem, the provisions of the theory of elasticity were used. Based on the principle of superposition, the process of medium deformation was divided into a number of stages, within which the particle conglomerate received a small increment in height, and the mechanical characteristics assumed a constant value. The proposed approach for determining the compaction pressure was based on the solution to a series of inverse elastic problems in which the displacement of the upper boundary of a conglomerate of rectangular particles was specified, and the normal stress that caused this increment was sought. To account for changes in the density of the medium during deformation, the method of sequential loads was used, within each of them, the density was taken to be constant and was determined depending on the magnitude of the total compressive deformation. The Hencky strain, which has the property of additivity, was used as a measure of deformation.

Results. As part of the study, an iterative model was constructed for calculating the compaction pressure of a particle conglomerate when the mechanical characteristics change depending on the degree of elastic compression. Series of test calculations were conducted using a conglomerate of wood particles, whose Young's modulus is described by a power-law density function. At each stage of deformation, the elastic constants of the material were assumed to be constant, depending on the density of the medium. Using the equilibrium equation and the superposition principle, based on the results of solving elastic deformation problems, the compaction pressure was calculated at each loading stage, and the dependence of the compaction pressure on the magnitude of the compressive deformation and the degree of compaction was constructed.

Discussion. The obtained results of deformation of the medium taking into account the change in mechanical characteristics depending on the degree of compression showed a clearly expressed nonlinearity of the curve of dependence of the compaction pressure on the compression deformation — with an increase in pressure, both the degree of compaction of the medium and the compression deformation increase. A comparative analysis of calculations using the example of a conglomerate of wood particles under the condition of a constant density of the medium and taking into account the change in density during the deformation process revealed a significant error in estimating the compaction pressure when averaging the density or when using constant density values corresponding to the initial (undeformed) or final state.

Механика

Conclusion . The constructed iterative model allows for calculating the compaction pressure of a particle conglomerate, taking into account changes in mechanical properties under elastic compression. The proposed approach accounts for the nonlinearity of the compaction pressure dependence on the degree of compaction of the medium and can be applied to briquetting processes for wood waste.

Acknowledgements. The authors would like to thank the Editorial board of the Journal and the reviewer for their professional analysis of the article and recommendations for its correction.

Funding Information. The research is done with the financial support from the Russian Science Foundation (grant no. 24-29-00089),

Введение. В различных производственных областях встречаются материалы с механическими характеристиками, зависящими от плотности. В частности, это гранулированные среды, конгломераты древесных частиц, композиционные материалы и др. Поведение таких материалов может существенно отличаться от классического, когда свойства остаются постоянными и не зависят от плотности. Часть вопросов оценки прочности и жёсткости для гранулированных сред рассмотрена в работе [1] , для песчаных форм — в работе [2] .

В настоящее время широко применяются процессы брикетирования конгломерата древесных частиц при вторичной переработке отходов деревообрабатывающей промышленности [3] , поэтому важно описать поведение частиц в процессе прессования. Вопросы оценки давления прессования обсуждались в работе [4] ; механический и термический анализ характеристик прессованных блоков с древесными включениями — в труде [5] ; оценка прочности древесного конгломерата — в работе [6] . Древесные опилки находят широкое применение при производстве строительных материалов, переработке в топливо и брикетировании. На процесс прессования влияют различные факторы [7] : так, влажность хранения отражена в работе [8] , влияние температуры — в труде [9] . Кроме того, древесные частицы используются в составе композиционных материалов, в частности при производстве биокомпозитов [10] , полимерных материалов [11] и многослойных композитов [12] .

Одной из ключевых задач моделирования деформирования частиц является выбор пресс-оборудования. Исследование [13] посвящено подбору прессовочных машин для получения твердого биотоплива путём гранулирования, брикетирования и механической обработки биомассы. При применении процедуры прессования конгломерата важным представляется моделирование напряжённо-деформированного состояния в процессе сжатия с учётом уплотнения среды. Изменение плотности влечёт за собой изменение механических характеристик среды, что влияет на точность расчёта требуемого деформирующего усилия и на выбор оборудования. Разработка более точных методик расчёта давления прессования с учётом сжимаемости среды важна для создания новых эффективных технологий и совершенствования существующих. Некоторые аспекты математического описания упругопластической задачи при сжатии для случая постоянных механических характеристик рассмотрены в работе [14] .

Анализ современного состояния вопроса показывает, что далеко не все программные пакеты способны учитывать изменение плотности и механических характеристик в процессе деформирования. Большинство систем CAE-анализа выполняют инженерные расчёты при заданных постоянных значениях физических и механических свойств. Поэтому актуальна разработка эффективных моделей и методик для оценки напряжённо-деформированного состояния сред при прессовании с учётом сжимаемости и изменения характеристик.

Цель исследования — разработать подход для расчёта давления прессования, необходимого для сжатия конгломерата частиц до заданной геометрии, с учётом влияния степени уплотнения на механические характеристики среды. В соответствии с этой целью поставлены следующие задачи:

• -    провести математическую постановку задачи упругого сжатия конгломерата частиц с учётом сжимаемости среды;

• -    построить итерационную модель расчёта напряжённо-деформированного состояния среды на основании решения серий обратных задач путём последовательных нагружений;

• -    провести тестовые расчёты напряжённо-деформированного состояния конгломерата частиц и построить зависимость давления прессования от деформации сжатия среды;

• -    оценить погрешность расчёта давления прессования при неучёте изменения плотности среды в процессе деформирования.

Методы исследования. Построение методики расчёта процесса деформирования конгломерата частиц с учётом сжимаемости среды будем проводить при следующих допущениях:

• -    поскольку в исследовании рассматривается сжатие среды, принимается условие сплошности, то есть конгломерат частиц равномерно заполняет исследуемый объём;

• -    масса среды остаётся неизменной в течение всего процесса прессования;

• -    процесс сжатия среды рассматривается в пределах упругого деформирования;

• -    выполняется принцип суперпозиции — независимо накопленные деформации на каждом этапе нагружения;

• -    прессование производится в абсолютно жёсткой матрице с помощью абсолютно жёсткого пуансона без трения, слои перемещаются равномерно по высоте, сдвиг исключён;

• -    вязкостью среды пренебрегаем, температура прессования остаётся постоянной;

• -    переменными механическими характеристиками, зависящими от плотности среды, являются модуль Юнга и коэффициент Пуассона;

• -    плотность среды является функцией деформации сжатия.

Геометрическая модель конгломерата частиц (рис. 1) имеет форму параллелепипеда с высотой h и постоянным основанием квадратной формы площадью S. В связи с прямоугольной формой конгломерата частиц модель будем рассматривать в декартовой системе координат, где ось 0x 3 направлена вдоль высоты параллелепипеда, а оси 0x 1 и 0x₂ лежат в плоскости основания параллелепипеда.

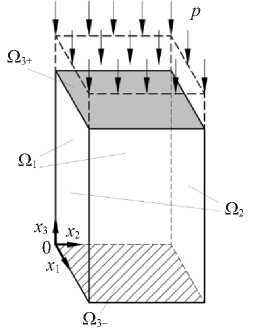
Рис. 1. Схема деформирования конгломерата частиц

Поскольку в процессе прессования давлением p осевая деформация сжатия по высоте возрастает по абсолютной величине, соответственно, изменяются плотность среды и, как следствие, ее упругие константы. Соответственно, модуль Юнга E и коэффициент Пуассона μ являются функциями плотности ρ: E = E (ρ), μ = μ(ρ). В качестве меры деформации будем использовать деформацию Генки.

Разобьем весь процесс деформирования среды на ряд этапов нагружения, в пределах каждого из которых будем задавать кинематическое условие в виде малого приращения верхней границы среды A h = A h * по высоте. На каждом этапе нагружения будем считать, что плотность среды остается постоянной и механические характеристики — модуль Юнга и коэффициент Пуассона не изменяются. На последующих этапах нагружения плотность среды и механические характеристики также остаются постоянными в пределах каждого этапа, но меняются в зависимости от величины суммарной деформации за все предыдущие этапы нагружения.

Будем рассматривать решение обратной задачи, принимая неизвестной величиной приращение давления на каждом этапе нагружения Δ p , тогда математическая постановка задачи исследования в соответствии с принятыми допущениями, будет включать в себя следующую систему уравнений:

• -    статические уравнения:

ЗАа_п / д x 1 = 0 , дАа 22 / д x 2 = 0 , дАа 33 / д x 3 = 0 , (1)

- физические уравнения:
А е 11 = rV аАои E ( р)	E ( р )( А а 2 2 +А° 33 ) ,	(2)
А e 22 = „ / х А о 22 E ( Р )	( х( А ° зз +А О 11 ) , E ( р )	(3)
А e 33 =      X А ° 33 E ( Р )	(( х^Оп + А о 22 ) , E ( Р )	(4)

Механика

• -    геометрические соотношения:

Л e 11 =Л e 22 = 0 , Л e 33 = ln ( 1 + Л h/h ) ,                                     (5)

• -    граничные условия:

u1 la, n2 = u 2 la,, n2 = 0, u 1ln3- = u 2ln3- = u 3ln3- = 0, u зк =-A h,

^Л ° ззк =^-Л P.                                         ⁽⁶⁾

где Δσ 11 , Δσ 22 , Δσ 33 — приращения напряжений; Δ e 11 , Δ e 22 , Δ e 33 — приращения упругих деформаций; u_i,i = 1,3 — компоненты перемещений.

На основании дифференциальных уравнений (1) и условие (6) приходим к соотношениям: Δσ 11 = const , Δσ 22 = const , Δσ 33 = –Δ p.

Учитывая, что в плоскости 0 x 1 x 2 отсутствуют перемещения, согласно соотношениям (3), (5) приведем систему уравнений (2), (3) к виду:

\ G     \ G ₂₂ =^{-        Л} p.                                          (7)

• ^{1    -} и ( p )

Подставляя соотношения (5) и (7) в уравнение (4), выразим приращение давления в следующем виде:

.           E ( p ) ( 1 ^- и ( p ) )     , Г, Л h 1

Л p = -7—  ' — ; ln 1 1 + I .

( 1 ⁺ и ( p ) )( 1 ^{- 2}и ( p ) ) I ^h J

Таким образом, при построении алгоритма расчета зададим дискретное изменение высоты конгломерата в зависимости от этапа нагружения:

h = { h(0) = h 0,... ,h(j ) = h 0 - j Л h, j = m,... h(n) = hend } , где h0 — начальная высота, соответствующая недеформированному состоянию конгломерата; hend — конечная высота конгломерата после всех этапов нагружения; j — этап нагружения.

Поскольку изменение высоты конгломерата известно, можно определить приращение деформации по высоте в пределах каждого этапа нагружения:

• ( j )        ⁽ h ⁽ j ) 1

^{Л e} 3з’ = ln [ j) J , j = ¹ ,n.

Полная деформация на текущем этапе нагружения будет определяться согласно принципу суперпозиции: j e 33 > = £ Л e 33 ) .

i = 1

Следует отметить, что выбор деформации Генки в качестве меры деформации обусловлен тем, что она обладает свойством аддитивности в отличие от относительной деформации, что позволяет суммировать деформации на отдельных этапах нагружения. При этом деформация Генки позволяет проводить расчет при больших деформациях.

Учитывая, что масса конгломерата и площадь основания остаются неизменными: m = const , S = const , перейдем к условию неразрывности в виде: ρ 0 h 0 = ρ h , откуда плотность среды будет определяться в зависимости от величины деформации сжатия Д e (j ) данного этапа нагружения согласно соотношению:

р ⁽ j ) = р ⁽ j ^{- 1 )} / exp Л e 33 ) .

Зная плотность среды на текущем этапе нагружения, модуль Юнга и коэффициент Пуассона на каждом этапе нагружения определяются в соответствии со степенью уплотнения некоторой функцией:

E ^{( j )} = E ^{( р} )l р = р ( j ) , ^иW = ^{и ( р} )l ₽ = ₽« .

Тогда приращение давления прессования будет определяться в виде:

...          E ( ^{р (} j ) ) ( 1 ^- и ( ^{р (} j ) ) )        ( h ⁽ j ) 1

Л p ⁽ j )=-  --------к----- 1 ln .

( 1 + и ( р ⁽ j ) ) )( 1 - 2и ( р ⁽ j ) ) ) I h ⁽ j ^{- 1 ) J}

Согласно принципу суперпозиции компоненты тензора напряжения на текущем этапе нагружения будут определяться в виде:

^j о ( 1 ) = £ л о( 1 ) , i = 1

j

О 22 V 22 ,

j о 3з V «

где приращения напряжений на каждом этапе определяются зависимостями:

^{Л о (} 1 j

= Ло 2 2 ) =

E ( р ^{2 J} ) ) И ( р ^{2 J} ) )           ( J ^J ) "I

----/  ’ ²--/--- In h— , Ло J

( 1 + Ц ( р ⁽ J ) ) )( 1 - 2ц ( р ⁽ J ))) [ h ^{2 J - 1 )} J

= Л p^(J).

Таким образом, процесс прессования конгломерата частиц представляется серией этапов нагружения, в пределах каждого из которых плотность среды и упругие константы считаются неизменными. На каждом этапе решается обратная упругая задача о сжатии среды. Входными данными для неё служат плотность, модуль Юнга и коэффициент Пуассона, значения которых определяются по суммарной величине деформации сжатия, накопленной на предыдущих и текущем этапах нагружения. В результате формируется последовательность обратных задач на основе данных об изменении высоты конгломерата частиц, по которой вычисляется изменение давле- ния прессования в зависимости от степени уплотнения среды.

Результаты исследования. На основании построенного подхода были проведены серии расчетов процесса деформирования конгломерата частиц на примере древесных опилок. Модуль Юнга (МПа) описывался функцией плотности (г/см ): E (ρ) = a ρ ^b , a = 6 500, b = 3,5 [15] . Выбор степенной зависимости обусловлен тем, что она достаточно хорошо описывает поведения конгломерата древесных частиц согласно работе [15] . Коэффициент Пуассона μ = 0,32 принимал постоянное значение, поскольку менее чувствителен к изменению плотности конгломерата, что отмечается в работе [16] . Кроме того, согласно экспериментальным исследованиям [17, 18] , наибольшее изменение коэффицента Пуассона имеет место при малых значения прессования, а при значениях давления свыше 20 МПа коэффициент Пуссона асимптотически приближается к постоянному значению. Начальная плотность конгломерата древесных частиц в недеформированном состоянии принималась: ρ 0 = 0,2 г/см³. Для проведения тестового расчета было выбрано 10 этапов нагружения. На каждом этапе верхняя граница конгломерата смещалась на величину Δ h = 10 мм, в результате чего высота конгломерата изменялась дискретно: h = {200, 190, …, 110} мм. На последнем этапе нагружения при h = 110 мм максимальное давление прессования составило 112 МПа, а плотность среды — 0,4 г/см³.

По результатам проведенных расчетов построена зависимость давления прессования от изменения деформаций сжатия (рис. 2) и от изменения плотности конгломера древесных частиц (рис. 3). С целью сравнительного анализа также были проведены серии расчетов при постоянной величине плотности и постоянном модуле Юнге для двух крайних случаев: при ρ = ρ 0 = const и при ρ = ρ end = ρ| h = 100 мм = const , т.е. когда плотность среды соответствует начальному недеформированному состоянию и конечному деформированному состоянию на последнем этапе нагружения; а также для случая осреднения плотности среды: при ρ = (ρ 0 + ρ end ) / 2 = const . Результаты расчетов при постоянных значениях плотности и упругих констант представлены на рис. 2.

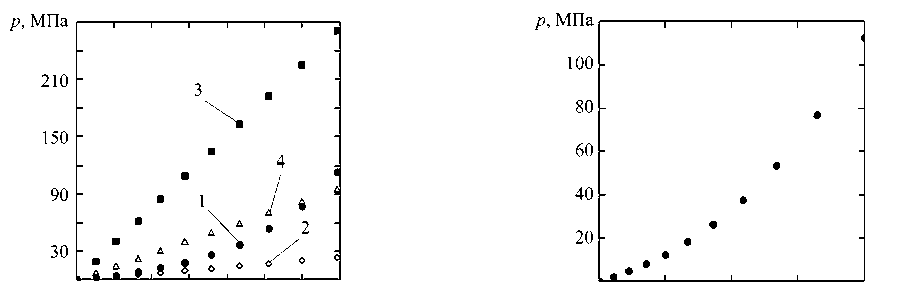
0,00     0,20      0,40     0,60 |e33|                              0,20    0,25    0,30    0,35 p, г/см3

Рис. 2. Зависимость давления прессования                   Рис. 3. Зависимость давления прессования от деформации сжатия:                                     от плотности среды

1 — при ρ = ρ( e ); 2 — при ρ = ρ0;

3 — при ρ = ρend;

4 — при ρ = (ρ0 + ρend) / 2

Механика

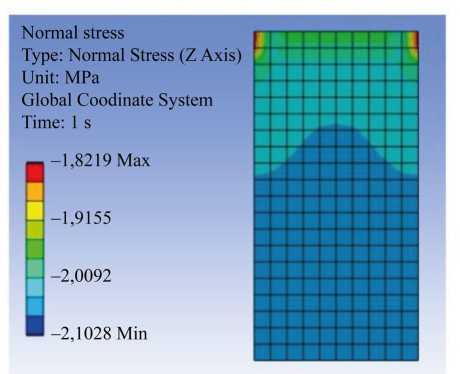
Согласно результатам решения обратной задачи упругого сжатия, для первого этапа нагружения при заданном перемещении верхней границы среды h⁽¹⁾ = 10 мм, приращения деформаций, напряжений и требуемое давление составляют: A e 33 ) = -0,051, Ao 33 ) = A p ( 1 ) = 2,041 МПа. Для оценки адекватности построенной модели был проведен конечно-элементный расчет прямой задачи нагружения в программном комплексе ANSYS при заданном внешнем давлении Δp⁽¹⁾ = 2,041 МПа. Поскольку программный комплекс требует задания постоянных характеристик среды, то конечно-элементный расчет проводился только за один первый этап нагружения [19] . Результаты расчета напряженно-деформированного состояния при упругом сжатии среды за первый этап нагружения представлены на рис. 4.

а)

Normal stress

Type: Normal Stress (Z Axis)

Unit: MPa

Global Coodinate System

Time: 1 s

-0,051445 Max

-0,052429

-0,053412

-0,054396 Min

б)

l,3247e-6Max

-3,4977

-6,9953

-10,493 Min

Normal stress

Type: Normal Stress (Z Axis)

Unit: MPa

Global Coodinate System

Time: 1 s

в)

Рис. 4. Результаты конечно-элементного расчета прямой задачи за первый этап упругого сжатия: а — распределение напряжений A o 33 ) МПа; б — распределение деформаций A e 33 ) ;

в — распределение перемещений и 31) (мм)

Обсуждение результатов. Согласно результатам расчетов (рис. 2, 3), с увеличением величины деформации сжатия растут требуемое давление прессования и степень уплотнения конгломерата частиц. Зависимость давления прессования от степени уплотнения имеет явно выраженный нелинейный характер. Зависимость давления прессования от продольной деформации сжатия (рис. 2, кривая 1) также описывается нелинейной функцией, поведение которой вполне адекватно аппроксимируется полиномиальной функцией третьего порядка. На рис. 2 видно, что при постоянной плотности конгломерата древесных частиц кривые зависимости давления прессования от величины деформации сжатия имеют слабо выраженный нелинейный характер. Соответственно, при фиксированной плотности среды кривые изменения давления прессования можно аппроксимировать линейными функциями.

Согласно сравнительному анализу, упрощение в виде использования величины плотности как постоянной характеристики в том случае, когда плотность среды существенно изменяется в процессе деформирования, может привести к существенным погрешностям. В частности, при использовании постоянной плотности конгломерата частиц ρ = ρ 0 , соответствующей начальному состоянию, погрешность расчета давления прессования возрастает до 80 %. При этом наибольшая погрешность достигается при максимальном давлении прессования. Для постоянного значения плотности ρ = ρ end , соответствующего конечному состоянию среды, результаты расчета на некоторых этапах нагружения отличаются более чем в 9,4 раза, а при осредненном значении плотности ρ = (ρ 0 + ρ end ) / 2 — более чем 3,4 раза.

Согласно данным на рис. 4, результаты, полученные с помощью метода конечных элементов при решении прямой задачи первого этапа нагружения согласуются с результатами, полученными при решении обратной задачи, согласно предложенному в данном исследовании подходу. Результаты, представленные на рис. 4, наглядно демонстрируют, что нормальные напряжения и деформации по высоте практически одинаковы в каждой точке тела, что подтверждает равномерность их распределения по высоте конгломерата при действии равномерного давления на верхней границе. При этом следует отметить, что на рис. 4 а , б имеет место градиент напряжений и деформаций вдоль продольной оси, что скорей всего является следствием сингулярности (особенно в зонах, выделенных красным цветом) — одного из недостатков метода конечных элементов, когда имеет место некорретное распределение напряжений и деформаций в области углов, при жестких закреплениях и т.д.

Заключение. По результатам исследования разработана итерационная модель, позволяющая рассчитать давление прессования конгломерата частиц, механические характеристики которого зависят от степени уплотнения при упругом сжатии. При проведении итерационных расчётов, с увеличением числа этапов нагружения и уменьшением шага приращения верхней границы конгломерата, может быть построена дискретная зависимость давления прессования от степени сжатия среды, которую затем можно аппроксимировать гладкой кривой. Согласно серии расчётов на примере упругой задачи прессования конгломерата древесных частиц с учётом изменения модуля Юнга и плотности среды, в процессе сжатия получена нелинейная зависимость давления прессования от степени уплотнения среды и деформации сжатия. По построенным графическим зависимостям учёт сжимаемости конгломерата частиц существенно влияет на нелинейность изменения давления прессования как функции плотности среды при деформировании. По данным сравнительного анализа расчёт напряжённо-деформированного состояния сред, плотность которых существенно изменяется в процессе прессования и влияет на механические характеристики, недопустимо выполнять при постоянных значениях плотности ввиду значительных погрешностей. Это позволяет заключить, что сжимаемость среды, связанная с изменением плотности конгломерата частиц в процессе сжатия, существенно влияет на оценку давления прессования. Построенная итерационная модель позволит на практике оценить максимальное давление прессования, необходимое для обеспечения упругого сжатия конгломерата частиц до заданной геометрии с учётом зависимости механических характеристик от плотности среды. Предложенный подход может найти практическое применение при выборе оборудования для реализации процессов брикетирования древесных частиц при вторичном использовании отходов деревообработки. Дальнейшим направлением исследований представляется разработка математических моделей расчёта напряжённо-деформированного состояния и давления прессования при деформировании конгломерата частиц с использованием пресс-форм сложной геометрии.