Итерационно-вероятностный метод решения линейного уравнения межотраслевого баланса

Введение. Задача оптимального планирования является одной из фундаментальных задач современной экономики. Производственные ресурсы могут сочетаться различными способами и обеспечивать при этом одинаковое количество выпускаемой продукции. Например, можно производить одно и то же количество продукции при больших финансовых затратах, но малых трудозатратах. Либо, наоборот, делать малые капиталовложения при больших затратах труда. Суть оптимального планирования состоит в выборе наиболее рационального способа производства продукции, который будет направлен на минимизацию затрат и максимизацию прибыли.

Одним из способов планирования производства является модель многоотраслевой экономики Леонтьева, а точнее, уравнение межотраслевого баланса. С его помощью удобно планировать валовой выпуск продукции для какого-либо периода времени по заданному вектору конечного потребления. Уравнение межотраслевого баланса представляет собой систему линейных алгебраических уравнений и решается такими методами, как метод Гаусса, Жордана — Гаусса, Крамера, Якоби, матричный и итерационный методы и др., каждый из которых имеет свои достоинства и недостатки.

Целью данного исследования является разработка нового стохастического метода решения уравнения межотраслевого баланса, основанного на использовании теории меры в вероятностном пространстве и метода простых итераций.

Суть модели Леонтьева и методы решения уравнения межотраслевого баланса. Модель Леонтьева используется для расчёта связи между отраслями через выпуск и потребление продукции разного вида [1]. На первом этапе строятся уравнения, описывающие балансовые соотношения между отраслями (1). Балансовый принцип связи различных отраслей промышленности состоит в том, что валовой выпуск Ай отрасли должен быть равным сумме объёмов потребления в производственной и непроизводственной сферах. В самой простой форме балансовые соотношения имеют вид:

х, = x_iY + x_i2 +... + %„ + у,; /=1,2,...,л

гдех,— валовой выпуск Ай отрасли; хй — объём продукции Ай отрасли, потребляемый >й отрас лью при производстве объёма продукции х/, у, —объём продукции Ай отрасли, предназначен ный для реализации (потребления) в непроизводственной сфере, или так называемый продукт конечного потребления.

В соотношениях баланса принято рассматривать стоимостный баланс, поскольку продукция различных отраслей имеет разные измерения.

На основе анализа экономики США В. В. Леонтьевым был установлен факт, что в течение длительного времени соотношения — очень слабо меняются и могут рассматриваться как посто- янные величины

В силу указанного факта можно сделать следующее допущение: для производства продукции у-й отрасли объёма Xj нужно использовать продукцию Ай отрасли объёма а^, где а„ = —— постоянное число. При таком допущении технология производства принимается ли-Хз нейной, а само допущение называется гипотезой линейности. При этом числа ад называются коэффициентами прямых затрат. Согласно гипотезе линейности имеем:

х,=а₉х/, i = v,...,n.                                    (2)

Тогда уравнения балансовых соотношений можно записать в матричной форме где

х = Ах + у

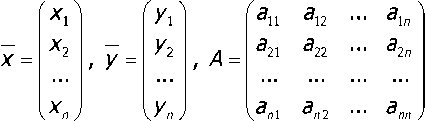
Описание матричного представления (4) и уравнение (3), собственно, и представляют собой модель Леонтьева. А уравнение (3) носит название уравнения линейного межотраслевого баланса.

Для его решения используются традиционные методы решения систем линейных алгебраических уравнений (СЛАУ), такие как матричный метод, метод Гаусса, Жордана — Гаусса, Крамера, простых итераций и т. д. Они подробно изложены во многих источниках, в частности в [2, 3]. Авторами данной работы предлагается использовать для решения уравнения (3) новый метод, имеющий ряд достоинств по сравнению с ранее известными, как применительно к решению уравнения линейного межотраслевого баланса, так и к другим задачам, в которых решаются СЛАУ. Применение стохастического метода решения СЛАУ к уравнению межотраслевого баланса. Рассмотрим линейное уравнение:

z(x) = C(x) + y,                                  (5)

где х еD(C) — искомый входной элемент; z(x)eF — выходной элемент; С— линейный оператор, в частности для конечномерного пространства, С— матрица пхп элементов; у eF — вектор правых частей.

Линейный оператор Сопределён на линейном многообразии D^C^ банахова пространства Е и отображает его в некое банахово пространство F.

Множество /?(С) — область определения оператора С. Совокупность всех z eF , для которых уравнение (5) разрешимо, является областью значений оператора С.

В уравнении (5) мы сталкиваемся с отображением, которое в конечномерном пространстве сужается до векторной функции случайных аргументов. Необходимо определить вероятностные характеристики векторной случайной величины Z по заданным вероятностным характеристикам векторной случайной величины X, связанной с величиной Z функциональной зависимостью 7=ф(Х).

Для того чтобы полностью охарактеризовать случайную величину, необходимо задать множество её возможных значений и дать способ определения и сравнения между собой вероятностей этих значений. Такая характеристика случайной величины называется её законом распределения.

Наиболее общей формой закона распределения случайной величины является её функция распределения [4]. Она имеет вид:

F ( у у у \ — р (( X X у 1 ( X У Й

Функция F (х) является вероятностной мерой.

Если Z— функция векторного случайного аргумента, то её функция распределения имеет вид:

ф(*о)<2О УхпУ2п где интеграл является л-кратным и распространён на все области, для которых выполнено неравенство, написанное под знаком интеграла.

В частном случае, когда функция ф монотонна в области возможных значений случайной величины X, существует только одна область, в которой выполнимо неравенство под знаком интеграла (6). В этом случае интеграл заменой переменных приведётся к виду:

^Fz^ = [-р(^(По),ф(П1),-,ф(П_я))-|/|ад1-^_ях                (7)

где п = ф(-х'); х = ф(п); 7— матрица Якоби вида I

Мп)

Dt\

Dx

Dz

Если матрица Якоби не обращается в ноль в области возможных значений, то существует с       с             Dx (DzV обратное отображение, причем — = — .

Dz \Dx

Дифференцируя (7), получим формулу, характеризующую закон сохранения меры для плотности вероятности векторной случайной величины Z.

ГДх) = Г(ф(х))|/|.(8)

В исследуемом авторами случае векторная величина Z является линейной функцией векторной случайной величины X, поэтому z = ф (х) = Сх + у, х = ф (z) = СА • z - СА • у .

Подставляя последнее выражение в (8), получим формулу для плотности вероятности линейной функции векторной случайной величины:

W-fy'-z-c-'-y^V(io)

Эта формула показывает, что при линейном преобразовании векторной случайной величины кривая плотности вероятности не изменяет своего характера, а только смещается относительно начала координат.

Применим формулу (10) для решения уравнения (5).

Как было сказано выше, предлагаемый в статье подход использует метод итераций, поэтому необходимо обозначить начальную область изоляции корня Do и привести уравнение (5) к виду х = Ах + у,                                  (И)

где А = С + Е, Е— единичная матрица.

Как видно, уравнение (11) представляет собой не что иное, как уравнение линейного межотраслевого баланса (3).

Для сходимости итерационного процесса достаточно, чтобы оператор А из уравнения (11) был сжимающим [5,6], т. е. ||Л|| < 1.

Если оператор А не сжимающий, то его необходимо привести к сжимающему виду.

Каждое последующее приближение хбудем находить по формуле ^хп=А-^х_п-1+У-                                (12)

Из (5) следует, что z (х„_ч) = С • х_п , + у, поэтому

=4-х„ , +у = /² '^ 2 Ч^а+е>_у = /³.%_{я з+}(/² *А*Е\у = ...

Таким образом, можно выразить приближение хна любой итерации через ль формулой хп = А" х0 +(/"1 + /"2 + ... + Е)-у .                           (13)

Обозначим (/"1 + /I”2 +... + £")•/ = D. Тогда х — Ап • х + D х — А п •(х — D\ Лп — л0      л0 — \лп u/ '

Подставим последнее уравнение в формулу (10):

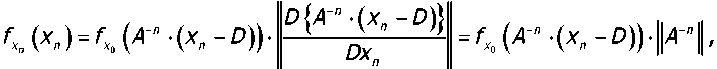
здесь внешние прямые скобки в определителе означают, что этот определитель берётся по абсО' лютной величине.

С учётом преобразований

Г.. У.) = f„ (л- ■ (х, - а-¹ - л-² -... - Е ) ■ у) ■ pr |,

где fXo ^А n -^хп - А"1 - А"2 - ...-Еуу^ — значение плотности вероятностной меры начального приближения Хо в области изоляции корня Оь.

Область Оь задаётся 2л точками, у каждой из которых п координат. Координаты точек области £2 на последующих итерациях определяются по формуле (12).

Область D сжимается к точке концентрации корня и вероятностная мера вырождается в этой точке в 5-функцию, если считать оператор и вектор правых частей не случайными. Каждое найденное по формуле (15) значение плотности вероятностной меры на Ай итерации имеет место в области О,.

Из полученной в результате подстановки формулы (16) видно, что, задав начальное приближение и определив плотность его вероятностной меры, можно найти плотность вероятностной меры хна любом шаге.

Заключение. В работе изложен принципиально новый метод решения систем линейных алгебраических уравнений и рассмотрено его применение для решения уравнения линейного межотраслевого баланса.

Предложенный подход выгодно отличается от используемых ранее методов тем, что в анализе участвует достаточно широкая окрестность решения. Также неоспоримым преимуществом метода является отсутствие затруднений с выбором начальной точки.

Кроме того, предложенный алгоритм имеет более широкую область применения, чем ранее известные. В частности, он может быть использован в случае нечёткого задания линейного оператора или вектора правых частей.