Итерационные методы расчёта параметров течений потоков жидкости в дроссельных окнах, зазорах клапанов, каналах и трубопроводах рулевых машин ракетных блоков

Компьютерное моделирование динамических процессов, происходящих в электрогидравлических рулевых машинах (РМ) систем управления вектором тяги ракетных двигателей [1] осуществляется путём численного интегрирования систем нелинейных дифференциальных уравнений, в которые входят выражения для расходов рабочей жидкости через дроссельные окна золотниковых гидрораспределителей (ГР), через зазоры предохранительных и переливных клапанов, а также через каналы и трубопроводы. При этом после каждого шага интегрирования необходимо иметь возможность определять мгновенные значения не только расходов, но и всех параметров, от которых зависят расходы.

Аналогично определение этих параметров требуется также при расчётах статических характеристик РМ [2, 3], которые основываются на решении систем нелинейных алгебраических и трансцендентных уравнений, в которых требуется иметь возможность определять мгновенные значения указанных параметров после каждой итерации.

Трудность определения точных мгновенных значений расходов и других параметров на каждом шаге интегрирования или на каждой итерации заключается в некоторой неопределённости, обусловленной тем, что значения расходов и безразмерных параметров течения потоков опосредованно (через число Рейнольдса) выражаются в конечном итоге сами через себя. Поэтому для точного их определения необходимо решать системы нелинейных алгебраических уравнений, при этом некоторые уравнения системы могут быть трансцендентными.

Постановка задачи исследований

Целью настоящей работы является разработка методов расчёта мгновенных значений расходов и других связанных с ними безразмерных параметров течения потоков жидкости, для каждого шага интегрирования при численном решении систем дифференциальных уравнений в процессе расчётов динамических характеристик электрогидравли-ческих РМ и для каждой итерации при решении систем нелинейных алгебраических уравнений в процессе расчётов их статических характеристик.

Итерационный метод расчёта расходов и безразмерных параметров течения потоков жидкости в дроссельных окнах золотниковых гидрораспределителей со стационарными гильзами

Особенностью жидкости через лотниковых ГР

истечения рабочей дроссельные окна зо-является зависимость потоков в них не только от числа Рейнольдса, но и от относительного противодавления на выходе дроссельного окна.

На основании проведённых исследований и полученных моделей потоков в таких ГР [4] предложен итерационный метод расчёта расходов и безразмерных параметров течений потоков рабочей жидкости. Он в общем случае заключается в решении модифицированным итерационным методом Зей-деля [5] следующей системы нелинейных алгебраических и трансцендентных уравнений:

Q = n ц ⁵ V2/P V I p н — p J sigⁿ⁽ p н ^- p с );

µ = spl(Re, ^– p );

ε = spl(Re, ^– p );

Re = -4 ^ ;

nΠνε p = pс /pн, где Q — расход рабочей жидкости через дроссельные окна золотникового ГР; n — количество дроссельных окон в гильзе; μ — коэффициент расхода дроссельного окна; S — площадь проходного сечения дроссельного окна; ρ — средняя плотность рабочей жидкости в дроссельном окне; pн — давление нагнетания; pс — давление слива; Re — число Рейнольдса; –p — относительное противодавление на выходе дроссельного окна; Π — смоченный периметр дроссельного окна; ε — коэффициент сжатия потока в дроссельном окне; ν — средняя кинематическая вязкость рабочей жидкости в дроссельном окне.

В этой системе уравнений коэффициент расхода дроссельного окна µ и коэффициент сжатия потока в дроссельном окне ε зависят одновременно от числа Рейнольдса Re и относительного противодавления на выходе дроссельного окна –p .

В большинстве случаев эти зависимости носят сложный нелинейный или трансцендентный характер, что иллюстрируется графиками, приведёнными в работе [4] для сливного сегментного дроссельного окна, и до недавнего времени для их аппроксимации различными авторами создавались достаточно сложные аналитические модели [6, 7] даже для одномерных зависимостей. С развитием компьютерной техники появилась возможность аппроксимировать такие зависимости с помощью метода многомерной кубической сплайн– интерполяции–экстраполяции (КСИЭ), разработанного автором [8]. Отличительная особенность данного метода заключается в том, что аналитические зависимости характеристик не требуются, а в расчётах статических или динамических характеристик РМ по соответствующим математическим моделям используются табличные представления экспериментальных данных. В рассматриваемом случае стационарных гильз ГР достаточно двухмерной КСИЭ.

Решение системы алгебраических и трансцендентных уравнений (1) также связано с большими трудностями из-за её чрезмерной жёсткости. Для возможности решения таких жёстких систем автором был модернизирован итерационный метод Зейделя [5], отличающийся тем, что приближениям неизвестных на каждой итерации присваиваются не значения их вычисленных ошибок, а сумма их предыдущих значений и части ошибки.

Для проверки возможности решения системы (1) была разработана процедура-функция, а также тестовая программа расчёта соответствующих параметров. При этом и программа, и процедура-функция были выполнены в среде Free Pascal [9].

Для наглядности и возможности сравнения с исходными данными для тестирования были выбраны зависимости µ = µ(Re, ^– p ) и ε = ε(Re, ^– p ) системы (1) для значений относительного противодавления на выходе сливного сегментного дроссельного окна ^– p = 1,0 и ^– p = 0,4. Результаты расчётов представлены на рис. 1.

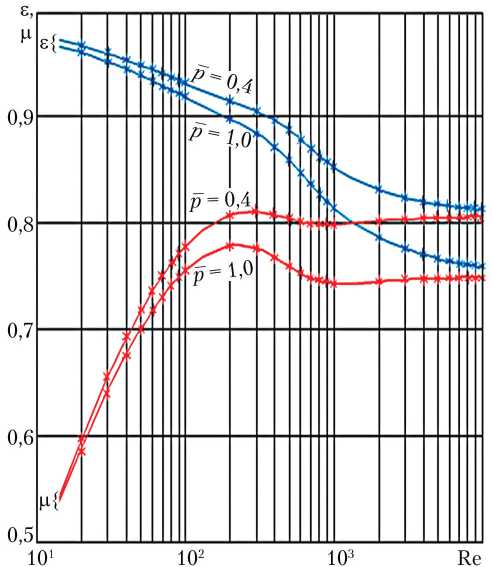
Рис. 1. Зависимости µ = spl(Re, ^– p ) и ε = spl(Re, ^– p ) для дроссельных окон в стационарной гильзе: µ — коэффициент расхода дроссельного окна; Re — число Рейнольдса; ^– p — относительное противодавление на выходе дроссельного окна; ε — коэффициент сжатия потока в дроссельном окне; ,    — исходные данные;

— результат вычислительного эксперимента (рисунок создан автором)

Как видно на графиках рис. 1, исходные данные и данные, полученные в результате вычислительного эксперимента, практически совпадают.

Итерационный метод расчёта расходов и безразмерных параметров течений потоков жидкости в дроссельных окнах золотниковых гидрораспределителей с вращающимися гильзами

Особенностью истечения рабочей жидкости через дроссельные окна золотниковых ГР с вращающимися гильзами является зависимость потоков в них не только от числа Рейнольдса Re, относительного противодавления на выходе ^– p , но и зависимость коэффициента расхода µ от безразмерного параметра Ψ, получившего название фактор вращения гильзы [10].

В рассматриваемом случае вращающейся гильзы ГР необходимо применение одной трёхмерной и одной двухмерной КСИЭ.

На основании проведённых исследований и полученных моделей потоков в таких ГР [10] предложен следующий итерационный метод расчёта расходов и безразмерных параметров течений потоков рабочей жидкости. Он в общем случае заключается в решении модифицированным итерационным методом Зейделя [5] следующей системы нелинейных алгебраических и трансцендентных уравнений:

Q = n µ S 2/ρ | p _н – p _с|sign( p _н – p _с);

µ = spl(Re, ^– p , Ψ);

ε = spl(Re, ^– p );

Re = ^{4 Q} ;

n Πνε

–p = pс/pн, где Ψ — фактор вращения гильзы, опре- деляемый выражением

Ψ = th( K _Ψδϑ), здесь K _Ψ — коэффициент аппроксимации, а δ и ϑ — безразмерные параметры, определяемые следующими выражениями:

δ V

δ = zг и ϑ = Vг , о где δг — толщина стенки гильзы; z — характерный размер дроссельного окна; Vг — линейная скорость кругового движения средней поверхности гильзы; Vо — скорость потока в дроссельном окне.

Для проверки возможности решения системы (2) была разработана процедура-функция, а также тестовая программа расчёта соответствующих параметров. При этом и программа, и процедура-функция были выполнены в среде Free Pascal [9].

Для наглядности и возможности сравнения с исходными данными для тестирования были выбраны зависимости µ = spl(Re, ^– p, Ψ) и ε = spl(Re, ^– p ) системы (2) для значений относительного противодавления на выходе сливного сегментного дроссельного окна ^– p = 0,2 при значениях фактора вращения гильзы Ψ = 0 и Ψ = 0,99. Результаты расчётов представлены на рис. 2.

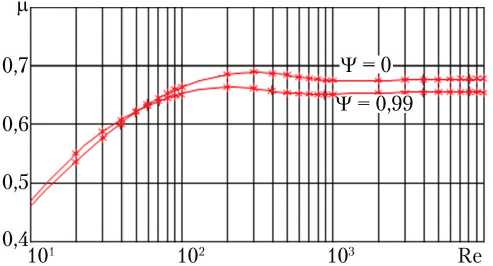
Рис. 2. Зависимости µ = spl(Re, Ψ ) при ^– p = 0,2 для дроссельных окон во вращающейся гильзе: µ — коэффициент расхода дроссельного окна; Re — число Рейнольдса; Ψ — фактор вращения гильзы; ^– p — относительное противодавление на выходе дроссельного окна; * — исходные данные; ^— — результат вычислительного эксперимента (рисунок создан автором)

Как видно на графиках рис. 2, исходные данные и данные, полученные в результате вычислительного эксперимента, практически совпадают.

Итерационный метод расчёта расходов и безразмерных параметров течений потоков жидкости в проходных сечениях предохранительных и переливных клапанов

Особенностью истечения рабочей жидкости через проходные сечения предохранительных и переливных клапанов в электрогидравлических РМ является отсутствие на выходе сечений противодавления [11]. Поэтому коэффициент расхода проходного сечения клапана µк и коэффициент сжатия потока в проходном сечении клапана εк зависят только от числа Рейнольдса Reк. Для их аппроксимаций достаточно двух одномерных КСИЭ.

Таким образом, итерационный метод расчёта расходов и безразмерных параметров течений потоков рабочей жидкости в проходных сечениях предохранительных и переливных клапанов заключается в решении модифицированным итерационным методом Зейделя [5] следующей системы нелинейных алгебраических и трансцендентных уравнений:

Q _к = µ_к S _к 2/ρ к p н.к ;

µк = spl(Reк);

εк = spl(Reк);

2 Q

Re = ^к , ^к π d _кν_кε_к

где Q _к — расход рабочей жидкости через зазор предохранительного клапана; S _к — площадь проходного сечения клапана; p _н.к — давление нагнетания в подводной магистрали клапана; Re_к — число Рейнольдса для клапана; d _к — диаметр подводной магистрали клапана; ρ_к — средняя плотность рабочей жидкости в проходном сечении клапана; ν_к — средняя кинематическая вязкость рабочей жидкости в проходном сечении клапана.

Для проверки возможности решения системы (3) была разработана процедура-функция, а также тестовая программа расчёта соответствующих параметров. При этом и программа, и процедура-функция были выполнены в среде Free Pascal [9].

Для наглядности и возможности сравнения с экспериментальными данными для тестирования были выбраны зависимости µк = spl(Reк) и εк = spl(Reк) системы (3). Результаты расчётов представлены на рис. 3.

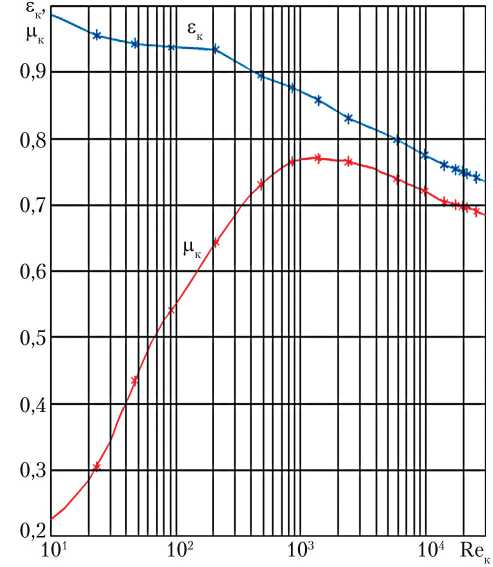
Рис. 3. Зависимости µк = spl(Reк) и εк = spl(Reк) для зазора клапана: µк — коэффициент расхода проходного сечения клапана; Reк — число Рейнольдса для клапана; εк — коэффициент сжатия потока в проходном сечении клапана; ,   — исходные данные; — результат вычислительного эксперимента (рисунок создан автором)

Как видно на графиках рис. 3, исходные данные и данные, полученные в результате вычислительного эксперимента, практически совпадают.

Итерационный метод расчёта расходов и безразмерных параметров течений потоков жидкости в каналах и трубопроводах

На основании проведённых исследований и полученных моделей потоков в каналах и трубопроводах РМ [12] предложен следующий итерационный метод расчёта расходов и безразмерных параметров течений потоков рабочей жидкости. В общем случае он заключается в решении модифицированным итерационным методом Зейделя [5], прошедшем апробацию в программах расчёта статических характеристик двухдроссельных и четырёхдроссельных рулевых машин, следующей системы нелинейных алгебраических и трансцендентных уравнений:

Q (т) = ⁵ к(т)V ^2/Pk_W (£^z i + \<т) /     V p ^- p J signc p_s ^- P d );

■ -1              D г

λк(т) = spl(Reк(т), η);

ζ_в.с = spl(Re_к(т), m );

ζ 1 = spl(Re к(т) , ξ 1 );

ζ n = spl(Re к(т) , ξ n );

ζ_в.р = spl(Re_к(т), m );

Re

к(т)

⁴ Q k(t)

^П D r ^V K ( T) ^,

где Q _к(т) — расход рабочей жидкости через канал (трубопровод); S _к(т) — площадь проходного сечения канала (трубопровода); ρ_к(т) — средняя плотность рабочей жидкости в канале (трубопроводе); ν_к(т) — средняя кинематическая вязкость рабочей жидкости в канале (трубопроводе); λ_к(т) — коэффициент трения по длине канала (трубопровода); Re_к(т) — число Рейнольдса для канала (трубопровода); p _s — давление на входе в канал (трубопровод); p _d — давление на выходе канала (трубопровода); l — длина канала (трубопровода); η — относительная шероховатость внутренней поверхности канала (трубопровода); ζ₁…ζ _n — коэффициенты местных гидравлических сопротивлений, обусловленных изменениями параметров русла течения потока; ξ₁…ξ _n — характерные изменения параметров русла течения потоков рабочей жидкости, выражаемые такими параметрами, как относительное изменение площади проходного сечения на его входе или выходе, а также угол изгиба и т. д; D _г — гидравлический диаметр канала (трубопровода), определяемый его формой:

D _г = d _к(т) при круглом сечении диаметром d _к(т);

D _г = a при квадратном сечении со стороной a ;

2 ab

D _г = a + b при прямоугольном сечении со сторонами a и b ;

D _г = D – d при кольцевом сечении с внешним D и внутренним d диаметрами.

Коэффициенты местных гидравлических сопротивлений ζ_в.с. и ζ_в.р характеризуются для внезапного сужения и внезапного расширения потока единым параметром m , который определяется как m = D / d , где D — больший диаметр; d — меньший диаметр.

Значения коэффициентов местных гидравлических сопротивлений, обусловленных изменениями параметров русла течения потока ζ₁…ζ _n , принимались равными нулю.

Значения коэффициентов местных гидравлических сопротивлений, обусловленных внезапным сужением потока ζ_в.с и внезапным расширением потока ζ_в.р при различных значениях числа Рейнольдса Re и параметра m представлены в таблице [13].

Значения ζ _в.с и ζ _в.р при различных значениях числа Рейнольдса Re и параметра m

m	Re
	10	20	40	100	200	500	1 000	2 000		4 000		5 000		10 000	20 000
Внезапное сужение потока ( ζ в.с)
0	5	3,35	2,10	1,4	1,15	0,94	0,75	0,60		1,00		0,85		0,6	0,50
0,1	5	3,20	2,00	1,3	1,04	0,82	0,64	0,50		0,80		0,75		0,5	0,45
0,2	5	3,10	1,84	1,2	0,97	0,70	0,50	0,40		0,60		0,60		0,4	0,40
0,4	5	2,80	1,60	1,0	0,78	0,50	0,35	0,25		0,45		0,50		0,3	0,30
0,6	5	2,60	1,35	0,8	0,50	0,35	0,24	0,15		0,35		0,35		0,2	0,20
Внезапное расширение потока ( ζ в.р)
0,1	3,1	3,0	2,15	1,7	1,65	1,70	2,00	1,60	0,81		0,81		0,81		0,1
0,2	3,1	2,8	1,85	1,4	1,30	1,30	1,60	1,25	0,64		0,64		0,64		0,2
0,4	3,1	2,4	1,50	1,1	1,00	0,85	1,05	0,80	0,34		0,36		0,36		0,4
0,6	3,1	2,15	1,25	0,8	0,60	0,40	0,60	0,50	0,15		0,16		0,16		0,6

Для проверки возможности решения системы (4) была разработана процедура-функция, а также тестовая программа расчёта соответствующих параметров. При этом и программа, и процедура-функция были выполнены в среде Free Pascal [9].

Для наглядности и возможности сравнения с исходными данными для тестирования была выбрана зависимость λк(т) = spl(Rек(т), η) для гидравлических гладких труб (η = 15). Результаты

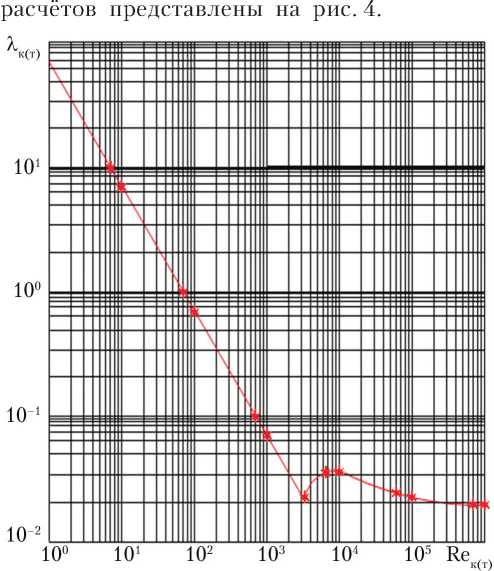
Рис. 4. Зависимость λ _к(т) = spl(Re_к(т)) для трубопровода: λ _к(т) — коэффициент трения по длине канала (трубопровода); Re _к(т) — число Рейнольдса для канала (трубопровода); * — исходные данные; ^— — результат вычислительного эксперимента (рисунок создан автором)

Как видно на графике рис. 4, исходные данные и данные, полученные в результате вычислительного эксперимента, практически совпадают.

Выводы

В результате проведённых исследований созданы итерационные методы расчёта мгновенных значений параметров течений потоков жидкости в дроссельных окнах золотниковых ГР, в зазорах предохранительных и переливных клапанов, в каналах и трубопроводах РМ ракетных блоков, значения которых необходимы на каждом шаге при численном интегрировании дифференциальных уравнений математической модели рулевой машины при расчётах динамических характеристик и после каждой итерации при итерационных методах расчёта её статических характеристик.

Применение в разработанных итерационных методах расчётов мгновенных значений параметров течений потоков жидкости методов КСИЭ и модифицированного итерационного метода Зей-деля позволило получать практически точное совпадение исходных данных зависимостей и данных, получаемых в результате проведения вычислительных экспериментов.