Итерационные методы статического анализа двухдроссельной электрогидравлической рулевой машины ракетных блоков

Рациональный выбор значений параметров электрогидравлических рулевых машин (РМ) [1, 2], получивших широкое распространение в системах управления космических блоков, может быть достигнут путем параметрической оптимизации, одним из этапов которой является проведение статического анализа.

Составляющими элементами статического анализа РМ являются методы расчета ее статических характеристик, к которым относятся:

• •    семейство скоростных характеристик РМ, т. е. зависимостей линейных (угловых) скоростей движения выходного органа РМ от командного сигнала и суммарной преодолеваемой нагрузки;

• •    силовая (моментная) характеристика РМ, т. е. зависимость усилий или моментов, развиваемых выходным органом РМ, от командного сигнала.

В процессе расчетов статических характеристик вычисляются некоторые дополнительные параметры и зависимости.

Существенное влияние на статические характеристики электрогидравлических РМ оказывают:

• •    напряжение питания электродвигателя РМ;

• •    температура рабочей жидкости РМ;

• •    местные гидравлические сопротивления конструкции РМ и ее электрогид-равлического усилителя (ЭГУ).

Учет указанных факторов при проектировании и оптимизации РМ достаточно сложен и поэтому требует разработки методов расчета статических характеристик РМ, позволяющих учитывать вышеприведенные факторы по их математическим моделям с заданной точностью и за минимальное время.

постановка задачи

В настоящей работе приводятся результаты разработки методов статического анализа варианта автономной однокаскадной электрогидравлической рулевой машины с двухдроссельным ЭГУ с отрицательным перекрытием с дроссельными окнами сегментной формы.

Расчетная схема принятого к рассмотрению варианта РМ представлена на рис. 1, а расчетная схема ее двухдроссельного ЭГУ — на рис. 2.

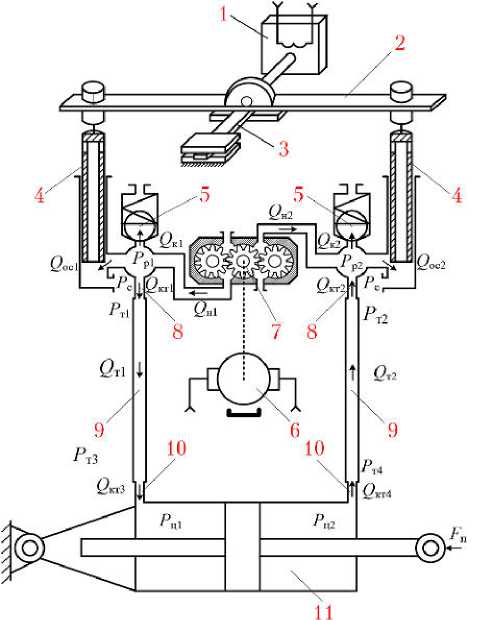
Рис. 1. Схема рулевой машины: 1 — поляризованное реле (электромеханический преобразователь); 2 — коромысло; 3 — плоская нагрузочная пружина; 4 — золотниковый плунжер; 5 — предохранительный клапан; 6 — электродвигатель; 7 — трехшестеренный насос; 8 — входной канал трубопровода; 9 — трубопровод; 10 — выходной канал трубопровода; 11 — силовой гидроцилиндр

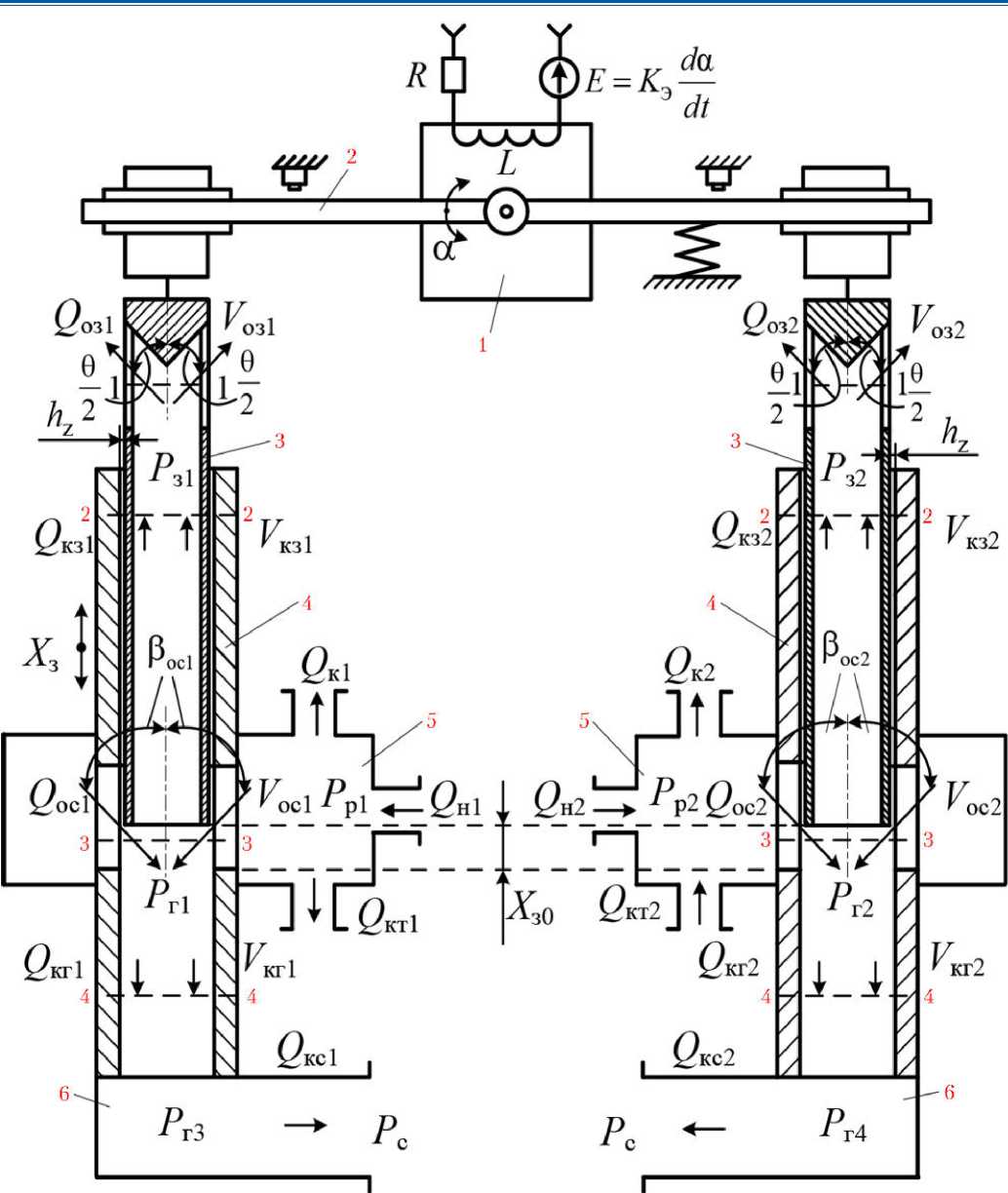
Рис. 2. Схема электрогидравлического усилителя (ЭГУ) рулевой машины: 1 — поляризованное реле (электромеханический преобразователь); 2 — коромысло; 3 — золотниковый плунжер; 4 — вращающаяся ось насоса; 5 — рабочая полость ЭГУ; 6 — канал слива

В основу разработки математических моделей статических режимов работы РМ и методов расчета ее статических характеристик были положены:

• •    методы комплексного моделирования физических свойств рабочих жидкостей, изложенные в работе [3];

• •    итерационные методы расчета параметров течений рабочей жидкости в каналах,

соединительных трубопроводах, проточных элементах и клапанах, представленные в работе [4];

• •    модификация метода Зейделя для решения систем нелинейных алгебраических и трансцендентных уравнений, приведенная в работе [5];

• •    методы расчета статических характеристик автономных однокаскадных РМ

  с двухдроссельным ЭГУ с отрицательным перекрытием, изложенные в работах [6, 7];

  • •    методы расчета статических характеристик двухдроссельного ЭГУ с отрицательным перекрытием, изложенные в работе [8];

  • •    результаты исследований рабочих процессов составляющих РМ, изложенные в работах [9–13].

  Математические модели статических режимов работы РМ получают из дифференциальных уравнений динамических режимов работы РМ путем приравнивания к нулю их старших производных.

  
  

  • уравнения, определяющие угловую скорость вращения вала электродвигателя (вала насоса) и потребляемый электродвигателем ток [8]

  
  

  ^{K 1 – K 2 K 3 – K 2 K 5 ( р р1 + р р2 )}    ;

  ^{[1 + K} 2 ^K 4⁽ ρ р1.с ν р1.с ⁺ ρ р2.с ν р2.с^)]

  
  
  
  

  I = э

  
  

  ^K 3 ^{+ K} 1 ^K 4⁽ ρ р1.с ν р1.с⁺ ρ р2.с ν р2.с⁾ ω ^{+ K} 5⁽ р р1⁺ р р2⁾

  
  

  ^{[1 + K} 2 ^K 4⁽ ρ р1.с ν р1.с ⁺ ρ р2.с ν р2.с^)]

  
  

  , (4)

  
  

  математическая модель статического режима работы и метод расчета силовой характеристики рулевой машины

  
  

  Под силовой характеристикой РМ понимается зависимость усилия, развиваемого силовым гидроцилиндром РМ, от командного тока. Силовую характеристику РМ определяют при условии предположения о заторможенном поршне силового гидроцилиндра, которое выражается соотношениями:

  
  

  п = 0; Q кт1 = Q т1 = Q кт3 = Q кт4 = Q т2 = Q кт2

  
  

  р _р1 = р _т1 = р _т3 = р _ц1; р _р2 = р _т2 = р _т4 = р _ц2, где р _р1, р _р2 — давления в рабочих полостях ЭГУ РМ; Q _кт1 – Q _кт4; Q _т1, Q _т2 — расходы через каналы и трубопроводы.

  Математическая модель статического режима работы для расчета силовой характеристики включает:

  • уравнение линейного перемещения золотникового плунжера [8]

  X з = a 1 I к – a 2 – a 3 F г ,              (1)

  где X _з — перемещение золотникового плунжера; F _г — гидравлическая сила, действующая на золотниковые плунжеры; а ₁… а ₃ — постоянные коэффициенты, определяе ^мы е как а 1 = ⁽ K M R a )/ K мп ; а 2 = ⁽ М стд R a )/ K _М п ; а 3 = R 2 / K _Мп, здесь K _M i — коэффициент моментной характеристики электромеханического преобразователя (ЭМП); М _стд — момент сухого трения движения, приведенный к валику ЭМП; K _МП — коэффициент позиционного момента от плоской нагрузочной пружины; R _а — плечо коромысла.

  На перемещение золотникового плунжера накладывается ограничение [8]

  | X _з| ≤ X _з^max,                     (2)

  где X _з^max — максимальное перемещение золотникового плунжера.

  
  

  где ю — угловая скорость вращения вала электродвигателя; I _э — потребляемый электродвигателем ток; K ₁… K ₈ — здесь и далее постоянные коэффициенты, определяемые как K 1 = U э / K ээ ; K 2 = R э / K ээ ; K 3 = ( M стэ + M стн )/ K мэ ;

  K ₄ = [ C _ж bm ²( z + 1)]/(2 K _мэ);

  K ₅ = [( C_f + 1) bm ²( z + 1)]/ K _мэ; K ₆ = bm ²( z + 1) – C_n ; K ₇ = C_рbm ²( z + 1); K ₈ = n _о 2,

  где U _э — напряжение питания электродвигателя; R _э — активное сопротивление якорной цепи электродвигателя, определяемое как R _э = R _э⁰ + K_tt , здесь R _э⁰ — значение активного сопротивления якорной цепи при 20 ° С; K t — температурный коэффициент; t — температура, ° С; K ээ — коэффициент электромагнитной скоростной связи электродвигателя; K _мэ — коэффициент моментной характеристики электродвигателя; M _стэ — момент сухого трения движения в электродвигателе; M _стн — момент сухого трения движения в насосе; C _ж — коэффициент жидкостного вязкого трения; C_f — коэффициент сухого трения, обусловленного давлением рабочей жидкости; b — ширина зубчатого венца шестерни насоса; m — модуль зацепления; z — количество зубьев шестерни насоса; C_n — коэффициент утечек, зависящих от скорости вращения вала насоса; C_p — коэффициент утечек, зависящих от перепада давления; Р _р1 . , р р _2с — средние значения плотности рабочей жидкости в зазорах предохранительных клапанов; у _р1с, у _р2с — средние значения кинематической вязкости рабочей жидкости в зазорах предохранительных клапанов;

  • уравнения давлений в рабочих полостях ЭГУ [8]

  Р pl = a 4 ^- Р p2 ^- a 5^{[1 +} a б ( Р р1.Л1.с ⁺ Р р2.с ^У р2.с ) ^{] X}

  
  

  ^Х ( Р р1Л1.с ) " ¹ Р p1

  
  
  
  

  ^- a 7^[1 + a 6⁽ Р

  
  

  р1.с ^ р1.с

  
  

  + Р

  
  

  р2.с р2.с^{)] X}

  
  

  ^X ^ ос1 ⁵ ос1 ^ 1/ Р р1.г1 ^pl ^- P Г1 1 sig ⁿ⁽ P p1 ^- Р Г1 ) ^-

  
  

  - a 8^[1 + a 6⁽ Р р1.сVр1.с + Р р2.с^ур2.с^{)] Q} к 1 ;        ⁽⁵⁾

  
  

p _p2 = a ₄ – p _p1 – a ₅[1 + a ₆( ρ _р1.с ν _р1.с + ρ _р2.с ν _р2.с)] × × ( ρ _р2.с ν _р2.с)^–1p_p2² – a ₇[1 + a ₆( ρ _р1.с ν _р1.с + ρ _р2.с ν _р2.с)] ×

× µ _ос2 S _ос2 1/ ρ _р2.г2 | p _p2 – p _г2|sign( p _p2 – p _г2) –

– a ₈[1 + a ₆( ρ _р1.с ν _р1.с + ρ _р2.с ν _р2.с)] Q _к2, (6) где p _г1, p _г2 — давления в полостях начала каналов гильз; Q _к1, Q _к2 — расходы рабочей жидкости через предохранительные клапаны; a ₄… a ₈ — постоянные коэффициенты, определяемые как а ₄ = ( K ₁ – K ₂ K ₃)/( K ₂ K ₅); а ₅ = K ₇/( K ₂ K ₅ K ₆); а ₆ = K ₂ K ₄; а ₇ = K ₈/( K ₂ K ₅ K ₆); а ₈ = 1/( K ₂ K ₅ K ₆);

• •    уравнение гидростатической силы, действующей на золотниковые плунжеры [8]

F _гс = а ₉( p _г1 – p _г2) + а ₁₀( p _з1 – p _з2),      (7)

где p _з1, p _з2 — давления в камерах золотниковых плунжеров; а ₉, а ₁₀ — постоянные коэффициенты, определяемые как а ₉ = S _т1; а ₁₀ = S _т2, здесь S _т1, S _т2 — площади внешней и внутренней торцевых поверхностей золотникового плунжера;

• •    уравнение стационарной гидродинамической силы [8]

F _гдс = ( p _г1 – p _г3)/ ( а ₁₁ + а ₁₂ λ _кг1) –

– ( p _г1 – p _з1)/( а ₁₃ + а ₁₄ λ _кз1) – ( p _г2 – p _г4)/( а ₁₁ + а ₁₂ λ _кг2) +

+ ( p _г2 – p _з2)/( а ₁₃ + а ₁₄ λ _кз2) + [ а ₁₇ µ ²_оз1( p _з1 – p _с)]/ ε _оз1 –

– [ а ₁₇ µ ²_оз2( p _з2 – p _с)]/ ε _оз2 – [ а ₁₈ µ ² _ос1 S _ос1( p _р1 – p _г1) ×

× cos( β _ос1)]/ ε _ос1 – [ а ₁₈ µ ² _ос2 S _ос2( p _р2 – p _г2) ×

× cos( β _ос2)]/ ε _ос2               (8)

где p _г3, p _г4 — давления в полостях перед каналами слива; λ _кг1, λ _кг2, λ _кз1, λ _кз2 — коэффициенты гидравлических потерь на трение по длине, соответственно, каналов гильз и каналов золотниковых плунжеров, определяемые в соответствии с работой [8] выражениями, которые удобно представить следующими функциональными зависимостями [4]

λ _кг1 = λ _к( p _г1, p _г3, ρ _г1.г3, ν _г1.г3, d _кг, l _кг, η _кг, ξ _кг.1, …, ξ _{кг. n} ); (9)

λ _кг2 = λ _к( p _г2, p _г4, ρ _г2.г4, ν _г2.г4, d _кг, l _кг, η _кг, ξ _кг.1, …, ξ _{кг. n} ); (10)

λ _кз1 = λ _к( p _г1, p _з1, ρ _г1.з1, ν _г1.з1, d _кз, l _кз, η _кз, ξ _кз.1, …, ξ _{кз. n} ); (11)

λ _кз2 = λ _к( p _г2, p _з2, ρ _г2.з2, ν _г2.з2, d _кз, l _кз, η _кз, ξ _кз.1, …, ξ _{кз. n} ), (12)

здесь ρ _г1.г3, ρ _г2.г4 — средние значения плотностей в полостях каналов гильз; ν , г1.г3

ν _г2.г4 — средние значения кинематической вязкости в полостях каналов гильз; ρ _г1.з1, ρ _г2.з2 — средние значения плотностей в полостях каналов золотниковых плунжеров; ν _г1.з1, ν _г2.з2 — средние значения кинематической вязкости в полостях каналов золотниковых плунжеров; η _кг, η _кз — относительные шероховатости внутренних поверхностей каналов гильз и каналов золотниковых плунжеров, соответственно; ξ _кг.1, …, ξ _{кг. n} , ξ _кз.1, …, ξ _{кз. n} — характерные изменения параметров русла каналов гильз и каналов золотниковых плунжеров; l _кг, l _кз — длины каналов гильз и каналов золотников, соответственно; d _кг, d _кз — диаметры каналов гильз и каналов золотниковых плунжеров, соответственно; µ _оз1, µ _оз2, ε _оз1, ε _оз2 — соответственно, коэффициенты расхода отверстий в золотниковом плунжере и коэффициенты сжатия потоков в отверстиях золотниковых плунжеров, определяемые выражениями, приведенными в работе [8], которые удобно представить в виде следующих функциональных зависимостей:

µ _оз1 = µ _оз( р _з1, р _с, ρ _з1.с, ν _з1.с, S _оз, П_оз); (13) µ _оз2 = µ _оз( р _з2, р _с, ρ _з2.с, ν _з2.с, S _оз, П_оз); (14) ε _оз1 = ε _оз( р _з1, р _с, ρ _з1.с, ν _з1.с, S _оз, П_оз); (15) ε _оз2 = ε _оз( р _з2, р _с, ρ _з2.с, ν _з2.с, S _оз, П_оз), (16)

здесь ρ _з1.с, ρ _з2.с — средние значения плотности рабочей жидкости в отверстиях золотниковых плунжеров; ν _з1.с, ν _з2.с — средние значения кинематической вязкости рабочей жидкости в отверстиях золотниковых плунжеров; S _оз — площадь проходного сечения отверстия в золотниковом плунжере, определяемая как S _оз = π d ²_оз /4; П_оз = π d _оз — смоченный периметр отверстия в золотниковом плунжере; µ _ос1, µ _ос2 — коэффициенты расхода сегментных дроссельных окон, определяемые выражениями, приведенными в работе [11], которые удобно представить в виде следующих функциональных зависимостей:

^µ ос1 ^{= µ} ос1⁽ р р1^, р г1^, ρ р1.г1

ν р1.г1^,   ос1^, ос1^, ос1^{, ξ} ос1 ^;

µ _ос2 = µ _ос2( р _р2, р _г2, ρ _р2.г2, ν _р2.г2, S _ос2, П_ос2, δ _ос2, ξ _ос2), (18)

где S _ос1, S _ос2 — площади проходных сечений дроссельных окон сегментной формы, определяемые выражениями [6]:

S ос1 = 0 при ( Х з0 – Х з ) ≤ 0,

S ос1 = S з + ( d о ²/4)arctg   [ d о /( d о – 2 X з0 + 2 X з )]² – 1  –[( d о – 2 X з0 + 2 X з )²/4]   [ d о /

о

– 2 X з0 + 2 X з )]² – 1

при 0 < ( X з0 – X з ) ≤ d о / 2;

S ос2 = 0 при ( Х з0 + Х з ) ≤ 0,

S ос2 = S з + ( d о ²/4)arctg [ d о /( d о – 2 X з0 – 2 X з )]² – 1 –[( d о – 2 X з0 – 2 X з )²/4]  [ d о /(d о – 2 X з0 – 2 X з )]² – 1

при 0 < ( X _з0 + X _з) ≤ d _о /2;

здесь и далее Xз0 — начальное открытие дроссельных окон сегментной формы; dо — диаметр окнообразующих отверстий в гильзе; Sз — остаточная площадь проходного сечения при полностью перекрытом сегментном дроссельном окне; Пос1, Пос2 — смоченные периметры сегментных дроссельных окон, определяемые выражениями [7]:

П ос1 = 0 при ( Х з0 – Х з ) ≤ 0,

П ос1 = П з + d о arctg    ^{( d о2 /4) + [( d о /2) – X з0 + X з ] 2}  + 2 ( d о ²/4) + [( d о /2) – X з0 + X з ]²     (21)

ос1 з о              (dо/2) – Xз0 + Xз                  о о з0 з при 0 < (Xз0 – Xз) ≤ dо/2;

П ос2 = 0 при ( Х з0 + Х з ) ≤ 0,

П = П + d arctg ^{( d о2 /4) + [( d о /2) – X з0 – X з ] 2} +2 ( d ²/4) + [( d /2) – X – X ]²    (22)

ос2 з о              (d /2) – X – X                   о          о         з0 з о /        з0 з при 0 < (Xз0 + Xз) ≤ dо/2, где Пз — значение смоченного периметра при полностью перекрытом сегментном дроссельном окне; δос1, δос2, ξос1, ξос2 — безразмерные параметры движущихся дроссельных окон и потоков в них, определяемые выражениями [8, 11]:

⁵ ос1

__________________ D г2 — D _Г 1 _______________. 2{[ d o ( Х зО — Х) — ( Х зО — ^Х з )Т ⁺ 0,25П_з} ’

δ

ос2

D г2 – D г1

2{[ d _э( Х зо + Х з ) — ( Х зо + Х з )²]⁰ ' ⁵ + 0,25П з };

^ξ ос1

^{ω n} o ^S ос1 ^ε oc1^{( D} г1 ^{+ D} г2^{) ;}

^{ω n} o ^S ос2 ^ε oc2^{( D} г1 ^{+ D} г2⁾

, 4 Q ос2

где D _г1, D _г2 — внутренний и внешний метры гильзы, соответственно; ε _ос1, ε _ос2 — коэф

ос2

диа-

фициенты сжатия потоков в сегментных дроссельных окнах, определяемые выражениями, приведенными в работах [8, 11], которые удобно представить в виде следующих функциональных зависимостей:

ε _ос1 = ε _ос1( р _р1, р _г1, ρ _р1.г1, ν _р1.г1, S _ос1, П _ос1, δ _ос1, ξ _ос1); (27)

ε _ос2 = ε _ос2( р _р2, р _г2, ρ _р2.г2, ν _р2.г2, S _ос2, П _ос2, δ _ос2, ξ _ос2), (28)

где Q _ос1, Q _ос2 — расходы рабочей жидкости, протекающей через дроссельные окна сегментной формы, определяемые выражениями [8, 11]

^Q ос1 ⁼ n о ^µ ос1 ^S ос1 ^2/ ρ р1.г1 ^| p p1 ^– p г1^| s ⁱ gn ⁽ р р1 ^– р г1^{); (29)}

^Q ос2 ⁼ n о ^µ ос2 ^S ос2 ^2/ ρ р2.г2 ^| p p2 ^– p г2^| s ⁱ gn ⁽ р р2 ^– р г2^{), (30)}

здесь n _о — количество дроссельных окон в гильзе; β _ос1, β _ос2 — углы истечения потоков рабочей жидкости в сечениях сегментных дроссельных окон золотникового гидрораспределителя, определяемые выражениями, которые удобно представить в виде следующих функциональных зависимостей [8, 11]

βос1 = βос1(χос1, δос1, ξос1, hz, Reос1);(31)

βос2 = βос2(χос2, δос2, ξос2, h–z, Reос2),(32)

здесь χ _ос1, χ _ос2 — относительные открытия дроссельных окон, определяемые выражениями [8, 11]:

χос1 = (Хз0 – Хз)/hz;(33)

χос2 = (Хз0 + Хз)/hz,(34)

где h_z — значение зазора меж_–ду золотниковым плунжером и гильзой; h_z — значение относительного зазора между золотником и гильзой, определяемое выражением [8, 11]

h_z = h_z / D _г1; Re_ос1, Re_ос2 — числа Рейнольдса потоков в сегментных дроссельных окнах, определяемые выражениями, приведенными в работах [8, 11], которые удобно представить функциональными зависимостями Re_ос1 = Re( р _р1, р _г1, ρ _р1.г1, ν _р1.г1, S _ос1, П_ос1, δ _ос1, ξ _ос1); (35)

Re_ос2 = Re( р _р2, р _г2, ρ _р2.г2, ν _р2.г2, S _ос2, П_ос2, δ _ос2, ξ _ос2); (36)

а11…а16 — постоянные коэффициенты, опреде-n ляемые как а„ = У£ ,/(2S2 ); а - l /(2d S );

11    ^^~кг.        кг 12 кг кг кг i 1

n a 13 - S.„ /(2StX а 14 - l„/<'d„SJ: а 15 = i = 1

nn

= 2mозSозcos(θ/2); а16 = 2nо, здесь ∑ζкг.i, ∑ζкз.i — i = 1 i = 1

суммы коэффициентов местных гидравлических сопротивлений, обусловленных изменениями параметров русла каналов гильз и каналов золотниковых плунжеров, соответственно;

• •    уравнение гидравлической силы, действующей на золотниковые плунжеры

F г = F гс + F гдс ;               (37)

• •    уравнения давлений в камерах никовых плунжеров [8]

р ₌ р             а 17^{(1/ µ 2} оз1⁾ ρ з1.с

• ^{з1     г1 ( а} 13^{+ а} 14 ^λ кз1^{) ρ} г1.з1 ^{+ а} 17^{(1/ µ 2} оз1^{) ρ} з1.с

  золот-

  
  

а17(1/µ2оз2)ρз2.с р2 = р2

⁽ а 13 ⁺ а 14 ^λ кз2⁾ ρ г2.з2 ⁺ а 17^{(1/ µ} оз2⁾ ρ з2.

; (38)

где а ₁₇ = 1/(2 m ² _оз S ²_оз) — постоянный коэффициент;

• уравнения давлений в полостях начала каналов гильз [8]

р _г1 = р _р1/ 1 + а ₁₈[ ρ _р1.г1/( µ ² _ос1 S ²_ос1)] ×

^{×    1/  (} а 11 ⁺ а 12 ^λ кг1⁾ ρ г1.г3 ^{+ (} а 19 ⁺ а 20 ^λ кс1⁾ ρ г3.с ⁺

^{+ 1/ (} а 13 ⁺ а 14 ^λ кз1⁾ ρ г1.з1 ⁺ а 17⁽ ρ з1.с^{/ µ 2} оз1^{) 2 ; (40)}

р _г2 = р _р2/ 1 + а ₁₈[ ρ _р2.г2/( µ ² _ос2 S ²_ос2)] × × 1/ ( а ₁₁ + а ₁₂ λ _кг2) ρ _г2.г4 + ( а ₁₉ + а ₂₀ λ _кс2) ρ _г4.с + + [ 1/ ^ ⁽ а 13 + а 14 ^- з 2^{) р} г2.з2 + а 17^{( р} з2.с / ^ оз2)] } ^ ⁽⁴¹⁾

а18…а20 — постоянные коэффициенты, опре-n деляемые как а18 = 1/(2n2о); а19 = ∑ζкс.i/(2Sк2с);

i = 1

n а20 = lкс /(2aксS2кс), здесь ∑ζкс.i — сумма коэф-

• уравнения давлений в полостях перед каналами слива [8]

_{р г3 = р г1}             ^{( а} 19 ^{+ а} 20 ^λ кс1^{) ρ} г3.с              _{;   (42)}

(а11 + а12λкг1)ρг1.г3 + (а19 + а20λкс1)ρг3.с р = р             (а19 + а20λкс2)ρг4.с            ;   (43)

^{г г} ( а + а λ ) ρ + ( а  + а λ ) ρ

11      12 кг2   г2.г4        19      20 кс2 г4.с

• •    уравнения перемещений затворов предохранительных клапанов [7]

Y _к1 = [ а ₂₁ – а ₂₂( µ ² _к1 S _к1/ ε _к1) + а ₂₃ µ ² _к1 S ²_к1] р _р1 – а ₂₄; (44)

Y _к2 = [ а ₂₁ – а ₂₂( µ ² _к2 S _к2/ ε _к2) + а ₂₃ µ ² _к2 S ²_к2] р _р2 – а ₂₄, (45)

где ε _к1, ε _к2 — коэффициенты сжатия потоков в клапанах, как и коэффициенты расходов, определяемые в соответствии с работой [12] системами уравнений, которые удобно представить функциональными зависимостями:

ε _к1 = ε _к( р _р1, р _с, ρ _р1.с, ν _р1.с, S _к1, Y _к1);      (46)

ε _к2 = ε _к( р _р2, р _с, ρ _р2.с, ν _р2.с, S _к2, Y _к2);     (47)

µ _к1, µ _к2 — коэффициенты расхода предохранительных клапанов, определяемые в соответствии с работой [12] системами уравнений, которые удобно представить функциональными зависимостями:

µк1 = µк(рр1, рс, ρр1.с, νр1.с, Sк1, Yк1);(48)

µ _к2 = µ _к( р _р2, р _с, ρ _р2.с, ν _р2.с, S _к2, Y _к2). (49) На перемещения затворов предохранительных клапанов налагаются ограничения [7]

0 ≤ |Yк1| ≤ Yкmax;(50)

0 ≤ |Yк2| ≤ Yкmax,(51)

здесь Y _к^max — максимальное перемещение затвора предохранительного клапана; S _к1, S _к2 — площади проходных сечений предохранительных клапанов, определяемые выражениями [12]:

S _к1 = { π Y _к1sin( Θ )[ d _ш + Y _к1sin( Θ /2)]}/2;   (52)

S _к2 = { π Y _к2sin( Θ )[ d _ш + Y _к2sin( Θ /2)]}/2, (53)

где Y _к1, Y _к2 — перемещения затворов клапанов; Θ — угол конусности седла клапана; d _ш — диаметр шарика затвора клапана; а ₂₁… а ₂₄ — постоянные коэффициенты, определяемые как а ₂₁ = π d ²_к/4 K _п; а ₂₂ = [2cos( Θ /2)]/ K _п; а ₂₃ = 8/( π d ² _к K _п); а ₂₄ = h ₀, здесь K _п — коэффициент упругости пружины клапана; d _к — диаметр подводной магистрали клапана; h ₀ — начальное поджатие пружины клапана;

• •    уравнения расходов рабочей жидкости, протекающей через предохранительные клапаны [12]

Q к1 = µ к1 S к1 2/ ρ _р1.c p _p1;            (54)

Q к2 = µ к2 S к2 2/ ρ _{р 2.c} p _p2 ;            (55)

• •    уравнения плотности и кинематической вязкости рабочей жидкости в полостях ЭГУ РМ, которые в соответствии с работой [3] можно определить следующими функциональными зависимостями:

ρ _р1 = ρ ( t , р _р1); ρ _р2 = ρ ( t , р _р2);

ρ _г1 = ρ ( t , р _г1); ρ _г2 = ρ ( t , р _г2);

ρ _г3 = ρ ( t , р _г3); ρ _г4 = ρ ( t , р _г4);

ρ _з1 = ρ ( t , р _з1); ρ _з2 = ρ ( t , р _з2); ρ _с = ρ ( t , р _с); (56)

/ ν

р1

= ν ( t , р _р1); ν _р2 = ν ( t , р _р2);

ν _г1 = ν ( t , р _г1); ν _г2 = ν ( t , р _г2); ν _г3 = ν ( t , р _г3); ν _г4 = ν ( t , р _г4);

ν _з1 = ν ( t , р _з1); ν _з2 = ν ( t , р _з2); ν _с = ν ( t , р _с), (57)

а их средние значения — выражениями [8]

ρ _р1.с = ( ρ _р1 + ρ _с)/2; ρ _р2.с = ( ρ _р2 + ρ _с)/2;

ρ _р1.г1 = ( ρ _р1 + ρ _г1)/2; ρ _р2.г2 = ( ρ _р2 + ρ _г2)/2;

ρ _г1.з1 = ( ρ _г1 + ρ _з1)/2; ρ _г2.з2 = ( ρ _г2 + ρ _з2)/2;

ρ _г1.г3 = ( ρ _г1 + ρ _г3)/2; ρ _г2.г4 = ( ρ _г2 + ρ _г4)/2;

ρ _з1.с = ( ρ _з1 + ρ _с)/2; ρ _з2.с = ( ρ _з2 + ρ _с)/2;

ρ г3.с = ( ρ г3 + ρ с )/2; ρ г4.с = ( ρ г4 + ρ с )/2;          (58)

золотникового плунжера (1) с учетом (2), перемещения затворов клапанов (44), (45) с учетом (50), (51), а также давлений в узловых точках — в рабочих полостях ЭГУ РМ (5), (6) и полостях начала каналов гильз (40), (41) — методом, изложенным в работе [5], при изменении командного тока I _к от нуля до I _к.max с шагом h_i , с последующим вычислением усилия F , развиваемого силовым гидроцилиндром РМ, по выражению

F = S п ( р р1 – р р2 ) – F п – F тр , (60)

где F _тр — сила сухого трения в силовом гидроцилиндре РМ; F _п — противодействующая нагрузка на штоке силового гидроцилиндра РМ.

При этом на каждой итерации вычисляются параметры по уравнениям (3), (4), (7)–(39), (42), (43), (46)–(49), (52)–(55), а перед входом в итерационный процесс при каждом новом значении командного тока I _к вычисляются значения плотности и кинематической вязкости рабочей жидкости в полостях ЭГУ РМ по выражениям (56), (57) и их средние значения — по выражениям (58), (59).

При отрицательных вычисляемых значениях усилия F , развиваемого силовым гидроцилиндром РМ, они обнуляются.

Здесь и далее при входе в итерационный процесс на каждом следующем шаге по командному току в качестве начальных значений вычисляемых параметров используются значения этих параметров, полученные на предыдущем шаге.

ν _р1.с = ( ν _р1 + ν _с)/2; ν _р2.с = ( ν _р2 + ν _с)/2;

ν р1.г1

ν г1.з1

ν г1.г3

( ν _р1 + ν _г1)/2; ν _р2.г2

( ν _г1 + ν _з1)/2; ν

( ν _г1 + ν _г3)/2; ν

г2.з2

г2.г4

( ν р2 + ν г2 )/2;

( ν _г2 + ν _з2)/2;

( ν _г2 + ν _г4)/2;

математическая модель статического режима работы и метод расчета скоростной характеристики рулевой машины

ν _з1.с = ( ν _з1 + ν _с)/2; ν _з2.с = ( ν _з2 + ν _с)/2;

ν _г3.с = ( ν _г3 + ν _с)/2; ν _г4.с = ( ν _г4 + ν _с)/2,     (59)

\

где t — температура рабочей жидкости; р ₁, р ₂ — давления в рабочих полостях Э^рГУ; р ^р2_г1, р _г2, р _г3, р _г4 — давления в полостях гильз ЭГУ; р _з1, р _з2 — давления в полостях золотников; р _с — давление в полости слива ( р _с = 0).

Метод расчета силовой характеристики РМ с двухдроссельным ЭГУ заключается

Под скоростной характеристикой РМ понимается зависимость скорости движения ее выходного органа под нагрузкой от командного тока. Скоростную характеристику РМ определяют из условия предположения о неразрывности потоков, из которого следует, что [7]

^Q кт1

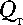
1 = Q кт3

^Q кт4

т2

в последовательном решении системы нелинейных алгебраических и трансцендентных уравнений, определяющих перемещение

где Q _т — обобщенный расход рабочей жидкости между рабочими полостями ЭГУ РМ; Q кт1 , Q кт2 , Q кт3 , Q кт4 , Q т1 , Q т2 — расходы рабочей жидкости через, соответственно, каналы трубопроводов и сами трубопроводы.

Математическая модель статического режима работы для расчета скоростной

характеристики включает уравнения (1)–(4), (7)–(59), а также:

• •    уравнения падений давления по длине комплексных трубопроводов [7]

∆ р ₁ = ∆ р _кт1 + ∆ р _т1 + ∆ р _кт3;         (61)

∆ р ₂ = ∆ р _кт2 + ∆ р _т2 + ∆ р _кт4,         (62)

здесь ∆ р _кт1, ∆ р _кт2 — падения давлений по длине входных каналов трубопроводов; ∆ р _кт3, ∆ р _кт4 — падения давлений по длине выходных каналов трубопроводов; ∆ р _т1, ∆ р _т2 — падения давлений по длине трубопроводов;

• •    уравнения падений давлений по длине каналов и трубопроводов [7]

∆ркт1 = (а25 + а26λкт1)ρр1.т1Qт2;(63)

∆рт1 = (а27 + а28λт1)ρр1.т3Qт2;(64)

∆ркт3 = (а25 + а26λкт3)ρт3.ц1Qт2;(65)

∆ркт4 = (а25 + а26λкт4)ρт4.ц2Qт2;(66)

∆рт2 = (а27 + а28λт2)ρт2.т4Qт2;(67)

∆ркт2 = (а25 + а26λкт2)ρт4.ц2Qт2,(68)

здесь λ _кт1, λ _кт2, λ _кт3, λ _кт4, λ _т1, λ _т2 — коэффициенты гидравлических потерь на трение по длине, соответственно, каналов трубопроводов и самих трубопроводов, определяемые в соответствии с работами [4, 7] функциональными зависимостями:

λ_кт1 = λ_к ( p _р1 , p _т1 , ρ_р1.т1 , ν_р1.т1 , d _кт , l _кт , η_кт , ξ_кт.1 , …, ξ_{кт. n} ); (69)

λ _кт2 = λ _к( p _т2, p _р2, ρ _р2.т2, ν _р2.т2, d _кт, l _кт, η _кт, ξ _кт.1, …, ξ _{кт. n} ); (70) λ _т1 = λ _т( p _т1, p _т3, ρ _т1.т3, ν _т1.т3, d _т, l _т, η _т, ξ _т.1, …, ξ _{т. n} ); (71) λ _т2 = λ _т( p _т4, p _т2, ρ _т2.т4, ν _т2.т4, d _т, l _т, η _т, ξ _т.1, …, ξ _{т. n} ); (72) λ _кт3 = λ _к( p _т3, p _ц1, ρ _т3.ц1, ν _т3.ц1, d _кт, l _кт, h _кт, ξ _кт.1, …, ξ _{кт. n} ); (73) λ _кт4 = λ _к( p _ц2, p _т4, ρ _т4.ц2, ν _т4.ц2, d _кт, l _кт, h _кт, ξ _кт.1, …, ξ _{кт. n} ), (74)

где η _кт, η _т — относительные шероховатости внутренних поверхностей каналов трубопроводов и самих трубопроводов; ξ _кт.1, …, ξ _{кт. n} , ξ _т.1, …, ξ _{т. n} — характерные изменения параметров русла каналов трубопроводов и самих трубопроводов;

• •    уравнение скорости движения поршня РМ [7]

V _п = |( a ₂₉/ K _квт)( р _р1 – р _р2) – ( a ₃₀/ K _квт)| ×

× sign[( a ₂₉/ K _квт)( р _р1 – р _р2) – ( a ₃₀/ K _квт)], (75)

где K _квт — коэффициент квадратичного вязкого трения, приведенного к поршню силового гидроцилиндра РМ, определяемого как [7]

K _квт = [( а ₂₅ + а ₂₆ λ _кт1) ρ _р1.т1 + ( а ₂₇ + а ₂₈ λ _т1) ρ _т1.т3 +

+ ( а ₂₅ + а ₂₆ λ _кт1) ρ _т3.ц1 + ( а ₂₅ + а ₂₆ λ _кт1) ρ _т4.ц2 +

+ (а27 + а28λт1)ρт2.т4 + (а27 + а28λт1)ρр2.т2]Sп3,(76)

здесь а25…а30 — постоянные коэффици-n енты, определяемые как а25 = ^Zkt//(2^Кт);

1'

n а26 = l.№dкт52кт); a27 - Zz„ /(2S^, г = 1

а28 = lт /(2dтSт2); а29 = Sп; а30 = Fтр + Fп, nn где ∑ζкт i, ∑ζтi — суммы, соответственно, i = 1      . i = 1

коэффициентов местных гидравлических сопротивлений, обусловленных изменениями параметров русла каналов трубопроводов и самих трубопроводов; l _кт, l _т — длины, соответственно, каналов трубопроводов и самих трубопроводов; d _кт, d _т — диаметры, соответственно, каналов трубопроводов и самих трубопроводов, где F _тр — сила сухого трения в силовом гидроцилиндре РМ; F _п — противодействующая нагрузка на штоке силового гидроцилиндра РМ; S _п — эффективная площадь поршня силового гидроцилиндра РМ, определяемая как

S = π ( d2 – d2), п   пш здесь dп — диаметр поршня силового гидроцилиндра; dш — диаметр штока силового гидроцилиндра;

• •    уравнения давлений в полостях трубопроводов и силового гидроцилиндра [7]

р т1 = рр1 – (а21 + а22λкт1)ρр1.т1Qт2sign(Qт);(77)

рт3 = рт1 – (а23 + а24λт1)ρт1.т3Qт2sign(Qт);(78)

р _т2 = р _р2 + ( а ₂₁ + а ₂₂ λ _кт2) ρ _р2.т2 Q _т²sign( Q _т); (79) р _т4 = р _т2 + ( а ₂₃ + а ₂₄ λ _т2) ρ _т2.т4 Q _т²sign( Q _т); (80)

рц1 = рр1 – ∆р1;(81)

рц2 = рр2 – ∆р2;(82)

• •    уравнение расхода через комплексный трубопровод [7]

Qт = SпVп;(83)

• •    уравнения давлений в рабочих полостях ЭГУ РМ [7]

p _p1 = a ₄ – p _p2 – a ₅[1 + a ₆( ρ _р1.с ν _р1.с + ρ _р2.с ν _р2.с)] ×

^{× (} ρ р1.с ν р1.с^{) –1} p ² p1 ^– a 7^{[1 +} a 6⁽ ρ р1.с ν р1.с ⁺ ρ р2.с ν р2.с^{)] ×}

× µ _ос1 S _ос1 1/ ρ _р1.г1  | p _p1 – p _г1| sign( p _p1 – p _г1) –

– a 8 [1 + a 6 ( ρ р1.с ν р1.с + ρ р2.с ν р2.с )]( Q к1 + Q т );     (84)

^X ( P p2.c ^V p2.c )^—1 P p2 ^— a 7^{[1 +} a 6⁽ P pLc ^V pLc ⁺ P p2.c ^V p2.c ) ^{] X}

^X Р ос2 ⁵ ос2 VVp PPZ ^ P p2^— P J ^Si gn ⁽ P p2 ^— P J ^—

- » 8 [1 ⁺ » 6 ( P p1.c V p1.c ⁺ P p2.c V p2.c )]( Q k2 — QY    ( ⁸⁵ )

• •    уравнения плотности и кинематической вязкости рабочей жидкости в полостях силового гидроцилиндра РМ и в полостях трубопроводов, которые в соответствии с работой [3] можно определить следующими функциональными зависимостями:

P ml = P ⁽ t , P ml ); P t2 = P ⁽ t , P т2 ) P t3 = P ⁽ t , P тЗ )

P t4 = p ⁽ t , p m4 );    Pm = p ⁽ t , p J;

Pц2 = p( t, р ц2);    Pc = p( t, pc);

^V m1 = ^{V (} t , P ml ); ^V t2 = ^{V (} t , P m2 ); ^V t3 = ^{V (} t , PтЗ^'

• ^v t4 = ^{v (} t , р т4 );     Ущ = V ⁽ t , р щ);

• Уц2 = V(t, Pц2); Vc = V(t, Pc),

и их средние значения — выражениями [7]

^P p1.m1

= ( P pi ⁺ P t1^)/2; P p2.T2 = ⁽ P p2 ⁺ P t2^)/2;

^P t1.t3   ^{( P} t1 ^{+ P} t3^{)/2; P} t2.t4   ^{( P} t2 ^{+ P} t4^)/2;

Ртз.1 = (Pt3 + Рц1)/2; Pt4.2 = (Pt4 + Рц2)/2;(

• ^V pi.T1 = ^{( V} pi ^{+ V} T1^)/2; V

• ^V t1.t3 = ^{( V} T1 ^{+ V} t3^{)/2; V}

  = ( V p2 ⁺ V t2 )/ ² ;

  = ( V t2 ⁺ V m4 )/2;

  
  

  р2.т2

  
  

  т2.т4

  
  

Vt3.1 = (Vt3 + Vm)/2; Vt4,2 = (Vt4 + Уц2)/2,(89)

где p _т1, p _т2, p _т3, p _т4 — давления в полостях трубопроводов; p _ц1, p _ц2 — давления в полостях силового гидроцилиндра.

Метод расчета скоростной характеристики РМ с двухдроссельным ЭГУ заключается в последовательном решении системы нелинейных алгебраических и трансцендентных уравнений, определяющих:

• •    перемещение золотникового плунжера (1) с учетом (2);

• •    перемещения затворов клапанов (44), (45) с учетом (50), (51);

• •    давления в узловых точках — в рабочих полостях ЭГУ РМ (84), (85) и полостях начала каналов гильз (40), (41);

• •    скорость движения поршня РМ (75) методом, изложенным в работе [5], при изменении командного тока I _к от нуля до I _к.max с шагом h_i .

При этом на каждой итерации вычисляются параметры по уравнениям (3), (4), (7)–(39), (42), (43), (46)–(49), (52)–(55), (61)–(74), (76)–(83), а перед входом в итерационный процесс при каждом новом значении командного тока Iк вычисляются значения плотности и кинематической вязкости рабочей жидкости в полостях ЭГУ РМ по выражениям (56), (57), (86), (87) и их средние значения — по выражениям (58), (59), (88), (89).

При отрицательных вычисляемых значениях скорости поршня силового гидроцилиндра РМ V _п они обнуляются.

апробация разработанных методов статического анализа

Результаты вычислительных экспериментов по определению статических характеристик автономной однокаскадной рулевой машины с двухдроссельным ЭГУ с отрицательным перекрытием и дроссельными окнами сегментной формы разгонного блока типа ДМ представлены на рис. 3–7.

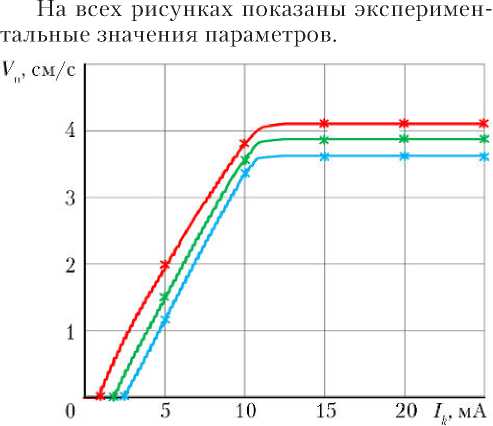
Рис. 3. Семейство скоростных характеристик РМ при противодействующих нагрузках на штоке РМ 0 ( ■ ), 1 000 ( ■ ) и 2 200 Н ( ■ ), напряжении питания 27 В и температуре 20 ° С: линия — расчет; * — эксперимент

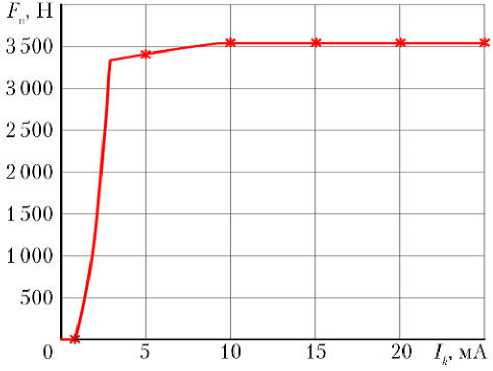
Рис. 4. Силовая характеристика РМ при напряжении питания 27 В и температуре 20 ° С: линия — расчет; * — эксперимент

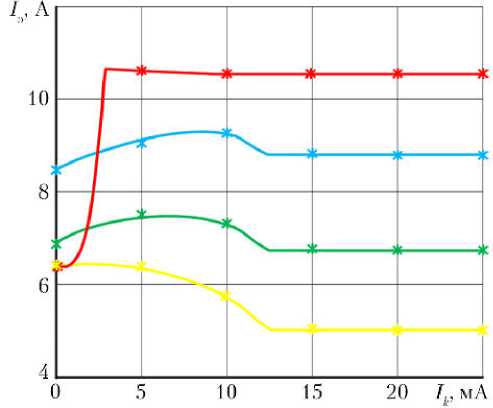
Рис. 5. Семейство зависимостей потребляемого тока РМ при противодействующих нагрузках на штоке РМ 0( — ); 1000( — ) и 2 200 Н ( — ) и заторможенном поршне ( ^— ) при напряжении питания 27 В, температуре 20 ° С: линия — расчет; * — эксперимент

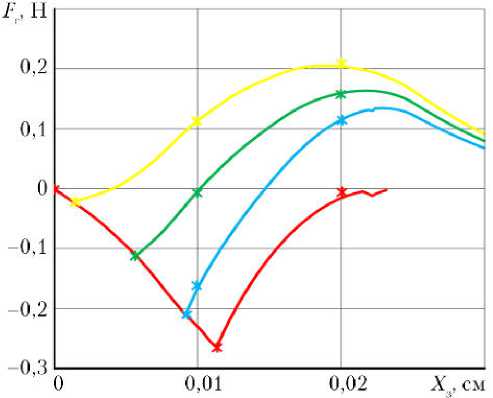
Рис. 6. Семейство зависимостей гидравлической силы, действующей на золотниковые плунжеры ЭГУ РМ, от перемещения золотникового плунжера при противодействующих нагрузках на штоке РМ 0 ( ^— ); 1 000 ( ^— ) и 2 200 Н ( ^— ) и заторможенном поршне ( ^— ) при напряжении питания

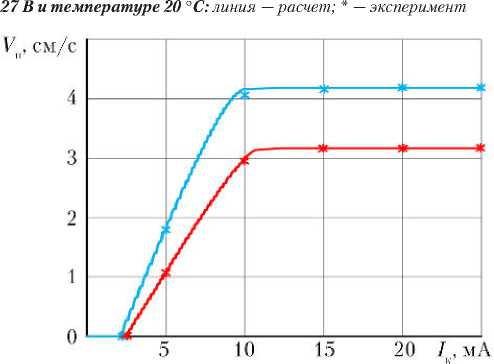
Рис. 7. Скоростные характеристики РМ при противодействующей нагрузке на штоке РМ 1000 Н, напряжении питания 23 В и температуре 50 ° С ( ^— ) и при напряжении питания 34 В и температуре -50 ° С ( ^— ): линия — расчет; * — эксперимент

Как видно из рисунков, расчетные графики и данные экспериментов практически совпадают, что указывает на корректность математических моделей, а также высокую точность и эффективность разработанных итерационных методов статического анализа рулевых машин.

заключение

В итоге проведенных разработок и исследований получены следующие основные результаты:

• •    разработаны математические модели статических режимов работы РМ с учетом местных гидравлических сопротивлений каналов и трубопроводов РМ и ее ЭГУ, а также с учетом зависимостей параметров РМ и ее ЭГУ от температуры, обеспечивающие погрешность вычисления характеристик не более 2% по сравнению с математическими моделями без учета указанных параметров и зависимостей, дающими погрешность вычислений до 15%;

• •    разработаны новые итерационные методы статического анализа РМ, включающие методы расчета статических характеристик РМ с учетом местных гидравлических сопротивлений, напряжения питания и температуры с заданной погрешностью вычислений и за минимальное время, и исследована их работоспособность.

Вывод по результатам проведенных в работе исследований: предложенные новые итерационные методы статического анализа РМ, основанные на решении нелинейных алгебраических и трансцендентных уравнений математических моделей статических режимов работы РМ, позволяют проводить расчеты статических характеристик РМ с заданной погрешностью вычислений и за минимальное время в широких диапазонах температур и напряжения питания.