Итерационный метод поиска авторотационных режимов автономной системы с одной степенью свободы

При исследовании механических систем с одной вращательной степенью свободы авторотационные режимы имеют особое прикладное значение (вращательные элементы станков, движение колесных машин в отсутствие проскальзывания, ветротурбины и т.д.). Если соответствующая математическая модель представлена в форме динамической системы с цилиндрической фазовой поверхностью, то режимам авторотации отвечают 2 π -периодические траектории. Описание условий существования и орбитальной устойчивости таких траекторий является одной из актуальных задач механики.

Поиск 2 π -периодических траекторий путем численного интегрирования уравнений движения с различными начальными условиями имеет существенный недостаток: при необходимости выявить влияние параметров модели на числовые характеристики периодических траекторий ресурсоемкость этого метода становится очень высока.

«Московский физико-технический институт (государственный университет)», 2017

Среди аналитических методов поиска периодических траекторий можно выделить методы, применимые к системам, близким к гамильтоновым: метод Пуанкаре–Понтрягина [1], метод Крылова–Боголюбова [2].

В настоящей работе предлагается численно-аналитический метод поиска периодических траекторий, не подразумевающий обязательного наличия малого параметра в системе. Метод представляет собой итерационную процедуру, подобную методу Пикара. На каждом шаге итерационного процесса строятся функции, приближенно описывающие 2 п -периодические траектории системы. Отметим, что функции, полученные на первом итерационном шаге, формально совпадают с результатом применения метода Пуанкаре– Понтрягина.

За счет того, что на каждом шаге уточняется информация только о 2 п -периодических траекториях, сложность метода при численной реализации значительно ниже, чем в случае численного построения полного фазового портрета системы.

2.    Постановка задачи

Пусть поведение механической системы с одной степенью свободы с угловой координатой, находящейся под действием неконсервативных сил, в том числе силы вязкого трения, описывается дифференциальным уравнением вида у = ш,    Со = wf (у, ш) — bw.

Здесь точкой обозначена производная по обезразмеренному времени, b — положительный безразмерный параметр, характеризующий коэффициент вязкого трения. Функция f ( у, ш ) — 2 п -периодическая и непрерывная по у , а также непрерывная и липшице-ва по ω (липшицева константа от ϕ не зависит) в некоторой ограниченной области {у Е [0 , 2 п ) ,ш Е G = ( ш 1 ,ш 2 ) } , где ш 1 ,ш 2 >  0. Требуется установить, существуют ли 2 п -периодические траектории системы (1), расположенные в области G , и описать такие траектории при их наличии.

Заметим, что если при некотором шо и некотором значении b = b(шо) траектория Ш(у;шо), проходящая через точку (0,шо), является 2п-периодической, то b(шо) удовлетво- ряет условию:

2 π

b ( ш о ) = 2 тт / f ( 9,ш ( 9 ’ ш о )) dy.

3.    Описание предлагаемого метода

Для поиска периодической траектории Ш(у ; ш о ) и соответствующего значения b ( ш о ) при заданном ω 0 предлагается следующая итерационная процедура:

Ш о ( у ; ш о ) = ш о ,

2 π

7 /     \ b о(ш о)

= 2 тт / f ( у,Ш о ( У ; ш о )) dу,

Ш к ( у ; ш о ) = ш о +

ϕ

j f ( t,W к- 1 ( t ; ш о )) dt —

b k - 1 ( ш о ) у,

2 π

7 /     \ bk (Ш о)

= 2тт /f (у,ш к(у;ш о)) d^, к > 1.

Докажем, что если липшицева константа функции f достаточно мала и при каждом к кривая Со к ( у ; ш о ) остается в области G , то при к ^ го последовательность функций

~

~

ш k ( у ; ш о ) равномерно сходится к ш ( у ; ш о ) и b k стремится к b ( ш о ), где ш ( у ; ш о ) — искомая 2 п -периодическая траектория системы (1) при b = b ( ш о ), проходящая через точку { 0 ,ш о } .

Заметим, что при ш > 0 системе (1) можно поставить в соответствие интегральное уравнение:

ϕ

— = f (у, ш) - b о ш =   (f (t, ш) - b)dt + ш0• dϕ

Пусть m — произвольное натуральное число. Рассмотрим невязку следующего вида:

Z n ( у ; ш о ) = ш n + m ( у ; ш о ) - ш n ( у ; ш о ) =

ϕϕ

У ( f ( t, ш n - 1+ m ( t ; ш о )) - ^b n - 1+ m ( ш о ) } dt - j ( f ( t, ш n - 1 ( t ; ш о )) - b n - 1 ( ш о ) } dt. оо

Учтем, что b k - 1 = тП J ^ ⁿ f ( у,ш k - 1 ( у ; ш о )) dу .

Также учтем, что поскольку f (у, ш) липшицева, то лишицевой является и функция f (у,ш) = f (у,ш)

-

1    2 п

2 П /_о ^{f (} у^,ш ) ^dУ.

Далее доказательство сходимости подобно доказательству сходимости классического метода Пикара, а именно:

|z n ( у ; ш о ) |

С

ϕ

j I f ( t,Ш n О

1+ m ( t ; ш о )) - f ( t, ш n - 1 ( t ; ш о )) I

dt С A

ϕ

j |ш n - 1+ m ( t ; ш о ) о

- ш n - 1 ( t ; ш о ) | dt,

где A — некоторая константа. Таким образом, получаем следующее соотношение:

lz _n ( у ; ш о ) | С А

^ϕ / о

|z n - 1 ( t ; ш о ) | dt.

В силу ограниченности рассматриваемой области имеем: |z о ( у ; ш о ) | С B = const, причем эта константа может быть выбрана не зависящей от m .

Получаем:

|z 1 ( у ; ш о ) | С АВу,

В ( Ау ) ^{2 |z} 2 ⁽ у ; ^ш о ) | ^С —2— , |z n ( у ; ш о ) | С BA^. n !

Поскольку рассматриваем систему на цилиндре, т.е. ϕ принимает значения на интервале [0 , 2 п ), то имеем: |z _n ( у ; ш о ) | С B ^^ nA^- • Следовательно, для произвольного е >  0 найдется N = N ( е ) такое, что при всех n > N ( е ) для произвольного m выполнено |z _n ( у ; ш о ) | < е . Таким образом, последовательность ci k ( у ; ш о ) фундаментальна. Следовательно, по критерию Коши рассматриваемая последовательность сходится. Обозначим ее предел ш ( у ; ш о ). Перейдем в (2) к пределу при k →∞ и получим:

ш ( у ; ш о ) = ш о +

ϕ

j f ( t,Ш(t ; ш о )) dt -b ( ш о ) у, о

2 п

^{b ( ш} о ) = 2 п / ^{f (} у^{,ш (} у ’ ^ш о )) ^dУ• о

Таким образом, для предела ш ( у ; ш о ) последовательности выполнено условие, означающее, что эта функция при b = b ( ш о ) определяет 2 п -периодическую траекторию системы (1), проходящую через точку (0 , ш о ).

Итак, при достаточно малом A имеет место сходимость указанной процедуры, которая в свою очередь означает существование периодической траектории ш(у ; ш о ) при соответствующем b ( ш о ) для всех тех значений ш о , для которых на каждом шаге выполнения процедуры ш k ( ^ ; ш о ) остается в области G .

4. Обсуждение результата в контексте известных итерационных методов

Итак, в результате применения предложенной итерационной процедуры получаем последовательность пар { b k ( ш о ) , ш к ( ^ ; ш о )}, сходящуюся к { b ( ш о ) , ш ( ^ ; ш о )}.

В частности, применение такой процедуры для некоторого набора {ш о i , i = 1 , ...,N} дает в пределе N точек бифуркационной диаграммы, описывающей зависимость 2 п -периодических траекторий системы (1) от параметра b , например: {b, ш (0) } .

Отметим, что если при некотором b = b о применить классический метод Пикара для численного интегрирования системы (1) с начальными условиями из набора {{ 0 ,ш о i },i = 1 ,...,N} на интервале ^ Е [0 , 2 п ), то мы получим N траекторий фазового портрета системы на цилиндре, в том числе, возможно, несколько из них окажутся близки к 2 п -периодическим траекториям системы (1). Тем самым, выполнив практически тот же объем численных расчетов, что и в первом случае, мы получим только точки бифуркационной диаграммы {b, ш (0) } , отвечающие конкретному b = b о .

Таким образом, предложенный метод по сравнению с классическим методом Пикара значительно уменьшает вычислительную сложность построения бифуркационной диаграммы 2 п -периодических траекторий системы (1).

Для проведения аналогии между предложенным методом и методами [1] поиска периодических решений в системах, близких к гамильтоновым, предположим, что требуется описать периодические траектории системы с одной степенью свободы, близкой к гамильтоновой, в некоторой области фазового пространства, в которой можно перейти к переменным действие–угол. Тогда в переменных действие I и угол ϑ уравнения системы можно представить в виде

•

•

У = P ( I ) ,     I = eQ ( У,I ) ,

где P ( I ) — производная от гамильтониана по переменной действие, е — малый параметр, функция Q ( У, I ) — 2 п -периодическая по У . В некоторой области G , где P ( I ) не обращается в ноль, можно в системе (3) перейти к производной по ϑ . Кроме того, предположим, что Q ( У, I ) P - 1 ( I ) = F ( У, I ) — В , где В — бифуркационный параметр, описывающий диссипацию, и что функция F ( У, I ) — липшицева в области G . Тогда можно рассматривать (3) как частный случай системы (1), при этом

т» = ^е ( F ( ^’I > ^{— В} > .

Применение итерационной процедуры (2) к уравнению (4), содержащему малый параметр, дает для периодического решения последовательные приближения, которые можно представить в следующем виде:

~

~

2 π

2л J' F ( У,Х о ( У ; I о ) ) ІУ,

В 1 ( I о ) = B о + еВ 1 ,

В 2 ( I о ) = В о + еВ 1 + е ² В 2 + O ( е 3 ) ,

( I о ) = У^ еВ + O ( е ^к +1 ), к >  3 .

i =0

I 1 ( У ; I о ) = I о + eI 1 ( У ) ,

^ 2 ( У ; I о ) = I о + eI 1 ( У ) + е ² 1 2 ( У ) + O ( е 3 ) ,

I k ( У ; I о ) = У e ⁱ I i ( У ) + O ( е ^{к +1} ) , В k

i=0

Таким образом, для системы вида (4) итерации (2) на к -м шаге позволяют получить 2 п -периодические траектории с точностью до O ( ^ k +1 ). Кроме того, получаем приближенное значение величины B ( I о ), при которой в окрестности I = I о существует периодическое решение системы (4). Существование следует (при условии, что I k ( $ ; I о ) G G для всех к ) из сходимости процедуры (2). Отметим, что на первом шаге получаем то же приближение, которое дает для периодической траектории системы (4) метод Пуанкаре–Понтрягина [1].

Естественно отметить, что разложение периодического решения уравнения (4) в ряд по малому параметру можно получить и путем прямой подстановки соответствующего ряда в уравнение (4) с последующим приравниванием нулю коэффициентов при одинаковых степенях ε . Однако такой прямой способ потребует для определения каждого следующего члена ряда вычислять не только интеграл от функции F ( ^, I ), но и частные производные этой функции все более высокого порядка.

5.    Пример

Рассмотрим следующую модель движения аэродинамического маятника, расположенного в стационарном потоке, с вертикальной осью вращения с ветроприемной пластинкой, закрепленной поперек державки:

dω dϕ

;² у ( C i ( а ) cos у — C d ( а)(ш + sin ^ )) — Ьш] ,

а = arctg ( — cos ^ ) , C i ( а ) = sin 2 а, C d ( а ) = 0 . 1 + sin ² а, ш + sin ^

r dϕ       ρSr ³

^ш = Vdt, a = "2J.

Здесь ϕ — угол поворота маятника, отсчитываемый от направления потока ветра, ω — безразмерная угловая скорость маятника, α — мгновенный угол атаки, r — расстояние от оси вращения до точки приложения аэродинамической силы (длина державки), V — скорость ветра, a — безразмерный параметр, характеризующий инерционные свойства маятника, ρ — плотность воздуха, — площадь ветроприемной пластинки, J — момент инерции маятника относительно оси вращения.

Значимость рассматриваемого маятника для практических приложений обусловлена тем, что он может служить моделью ветроприемного элемента ветроэнергетической установки с вертикальной осью вращения (типа Дарье), в последнем случае параметр b характеризует электрическую нагрузку в цепи генератора ветроустановки [3]. Отметим, что модель (5) является достаточно простой, более сложные математические модели подобных аэродинамических систем рассматривались, например, в [4–8].

В работе [9] на основе применения метода Пуанкаре—Понтрягина была построена бифуркационная диаграмма периодических траекторий уравнения (5) в зависимости от параметра b для случая a << 1. При этом приближение 2п-периодической траектории пред- ставляло собой на развертке фазового цилиндра прямую ω ≡ ω0 .

Применим итерационную процедуру (2) для построения бифуркационной диаграммы

{b ( ш о ) , ш (0; ш о)}

2 п -периодических траекторий системы (5) при конечном значении пара

метра a . Для примера рассмотрим случай a = 0 . 2.

На рис. 1 приведены итерации

|^bk ^{( ш} о ) , ^ш о}

к = 0 ,..., 13, для искомой бифуркационной

кривой. На выносном рисунке в увеличенном масштабе показана область, где сходимость

наиболее медленная, в этой области приведены несколько последних итераций: с 7-й по 14-ю. Эта же область отмечена на основной диаграмме пунктирным прямоугольником. Выносными цифрами на рисунках обозначены номера соответствующих итераций.

На рис. 2 показаны итерации построения кривых шk(^; шо) для случая шо = 0.5, а так- же результат построения соответствующей периодической траектории путем численного интегрирования уравнения (5) при b = 0.2106 методом Рунге-Кутты. Приближенное решение шк(^;шо), полученное на 4-й итерации предложенного метода, на рисунке визуально неотличимо от решения, полученного прямым интегрированием.

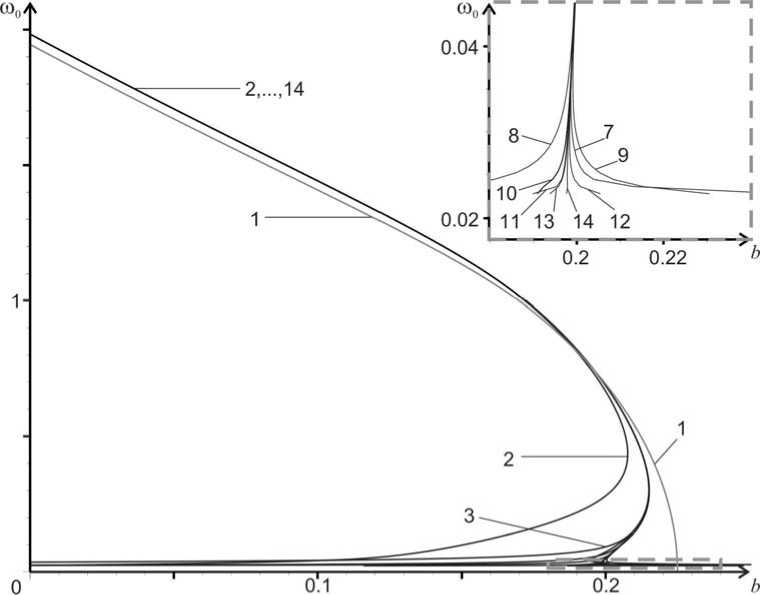
Рис. 1. Пример последовательных приближений бифуркационной диаграммы периодических траекторий

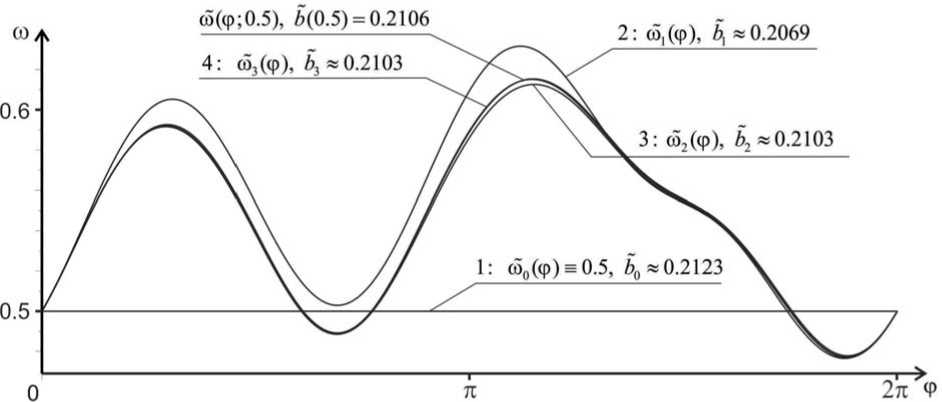
Рис. 2. Пример последовательных приближений периодической траектории

6.    Заключение

Предложенный в работе итерационный метод позволяет описать 2 п -периодические траектории динамической системы на цилиндре в зависимости от параметра системы, характеризующего диссипацию энергии (например, коэффициент вязкого трения в оси вращения).

Приведен пример построения бифуркационных диаграмм периодических траекторий одной механической системы маятникового типа на основе предложенного метода. За счет того, что на каждом шаге уточняется информация только о периодических траекториях, сложность метода при численной реализации значительно ниже, чем в случае численного построения полного фазового портрета системы.

Отметим, что итерационная процедура (2) может рассматриваться как развитие конструктивного метода поиска авторотационных режимов, предложенного в [9], где исследуемая система была близка к гамильтоновой и удовлетворяла условиям теоремы Пуанкаре– Понтрягина [1].

Работа выполнена при финансовой поддержке РФФИ (гранты №№ 15-01-06970, 16-31-00374, 17-08-01366).