Итерационный метод восстановления кусочно-постоянных изображений при известных границах областей

Кусочно-постоянные и близкие к таковым изображения являются достаточно распространёнными моделями регистрируемых полей яркости. Их восстановление после сглаживания, дискретизации и зашумления представляется интересным как с точки зрения теории, так и для многих приложений. Примером подобного приложения является мониторинг (регулярное наблюдение) сельскохозяйственных угодий на основе космических снимков [1]. Изображение угодий, как правило, имеет вид, близкий к кусочно-постоянному, границы областей мало меняются с течением времени и могут быть очерчены один раз по снимку высокого разрешения. После фиксации границ областей можно использовать для мониторинга снимки низкого разрешения, получаемые с более высокой частотой и имеющие существенно меньшую стоимость. Иными словами, предлагаемое восстановление изображений открывает возможность получения характеристик яркости, усреднённых по областям, с геометрической точностью, соответствующей снимкам высокого разрешения, но периодичностью снимков низкого разре- шения, что делает значительно доступнее процесс мониторинга и снижает требования к пространственному разрешению используемых данных.

На рис. 1 задача восстановления иллюстрируется на примере изображений участка земной поверхности, полученных со спутников Landsat (разрешение 32 метра) и Terra (разрешение 250 метров), с наложенными на них векторными границами.

Постановка задачи

Используемая в постановке задачи модель наблюдения показана на рис. 2. Пусть исходное изображение x ( t 1 , t 2 ), заданное в непрерывных координатах t 1 , t 2 , является кусочно-постоянным:

x ( t_v 1 2 ) = a i ,

( 1 1 , 1 2 ) ^e D i ,         i = О- 1 - 1,

D i П D =0 ,     i * j                       (1)

N - 1

u Di=D, i =0

LANDSAT

г)

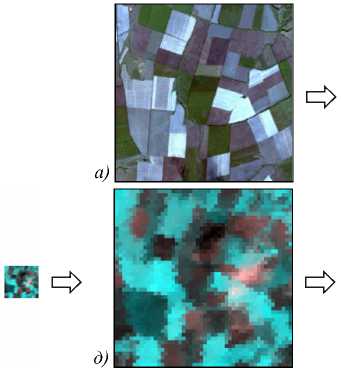
Рис. 1. Схема задачи восстановления кусочно-постоянных изображений для спутниковых изображений:

б)

е)

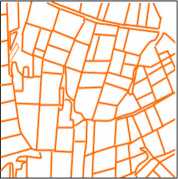
a) изображение среднего (32 м) разрешения, б) обрисовка векторных границ, в) сохранение векторных границ в ГИС, г) изображение низкого разрешения (250 м), д) интерполяция изображения г) до наземного шага дискретизации 32 м, е) наложение векторных границ на результаты интерполяции, ж) усреднение яркости внутри векторных границ

Рис. 2. Модель наблюдения

где a_i – значение яркости изображения в области D_i , I – число областей разбиения, D – область определения изображения.

Наблюдаемое дискретное изображение x_d ( n ₁, n ₂) формируется под действием искажающей линейной инвариантной к сдвигу системы с импульсной характеристикой (ИХ) h ( t ₁, т ₂) [2]

Х1 (t, 12) = J J , h (T1, t2 ) x (, - T1,12 T;) d^idT2, (2) пространственной дискретизации искаженного изображения с шагом T по координатам x 2 ( ni, n 2 ) = xi ( ti, t 2 )| ,,= nT ,                                    (3)

12 = n T и добавления шума xd (ni,n2) = x2(ni,n2) + v(ni,n2),                      (4)

где T – шаг дискретизации по координатам, ( n ₁, n ₂) – целочисленные индексы, v ( n ₁, n ₂) – случайные искажения пикселов.

Процесс восстановления в самом очевидном варианте выражается в интерполировании искажённого изображения:

x 3 ( t i , t 2 ) = EE x d ( t i , t 2 ) I ( t i ^- n i T , t 2 ^{- n} 2 ^T ) , ⁽⁵⁾ n ₁ n ₂

где I ( t ₁, t ₂) – интерполирующая функция, и приведении его к кусочно-постоянному виду путём усреднения по областям:

JJ X 3 ( T i , ^t 2 ) d ^T i d ^T 2

y ⁽ t i , t 2 ) = a i = —                     ,

JJ d T i d T 2                            ⁽⁶⁾

D i

( t ₁, 1 ₂ ) e D i ,         i = 0.. I - 1.

Однако оценка (6) весьма грубо описывает изображение (1) при больших значениях шага дискретизации T и широкой функции h ( t ₁, t ₂) .

Задача состоит в получении более точной оценки исходного изображения (1) при известном разбиении на области и наблюдаемом изображении (4).

Алгоритм

Если пренебречь шумовыми искажениями (4), то связь исходного изображения (1) и его оценки (6) можно представить в виде действия некоторого линейного оператора A (здесь и ниже запись аргументов для краткости опускаем):

y = Ax .

Известно, что если оператор A имеет обратный оператор A-1, линейный оператор J - A (где J - то- ждественный оператор) является ограниченным и выполняется условие

|| J - A || < 1,                                                   (8)

то существует единственное разложение обратного оператора A ^{- 1} в ряд Неймана [3]:

co

A ^{- 1} = J + E ( J - A ) n .                          (9)

n = 1

На этом факте основана итерационная схема восстановления Ван–Циттерта. Применяя вместо обратного оператора разложение (9) и выполняя последовательное суммирование, получаем приближения искомого решения x ^{( n )} :

X ⁽⁰⁾ = y , X ^{( n} ) = y + ( J - A ) x ^{( n - 1)}, n >  1.              (10)

В рассматриваемой нами задаче оператор искажений представляет собой композицию операторов сглаживания A ₁ (формула (2)) , дискретизации A ₂ (формула (3)), интерполяции A ₃ (формула (5)) и усреднения внутри границ областей A ₄ (формула (6)):

A = A ₄ A ₃ A ₂ A ₁.                                (11)

Очевидно, что оператор искажений в таком случае не имеет обратного, так как оператор дискретизации является вырожденным. Это означает две возможных ситуации: либо ряд (9) расходится, либо сходится, но к другому решению. В условиях отсутствия обратного оператора, а значит, принципиальной невозможности получить точное решение представляет интерес исследование свойств решения, получаемого в случае формального применения итерационной схемы (10).

Для сходимости ряда (9) необходимо, чтобы выполнялось условие (8). Условие (8) легко проверяется (а при необходимости и обеспечивается путём несложной модификации итерационной процедуры, см., например [3]) только для A ₁ . Однако несложно доказать, что операторы A ₂ , A ₃ , A ₄ являются положительными и нерасширяющими:

||A, || < 1, i = 2,3,4                                         (12)

и что этого достаточно, чтобы при выполнении условия (8) отдельно для сжимающего оператора A ₁ это условие выполнялось и для всей композиции (11).

Правило остановки итераций

Поскольку знания об идеальном сигнале отсутствуют, то недоступна для непосредственного измерения и погрешность приближенного решения

8 = x - x ^{( n} ) .                                             (13)

Однако можно вычислить погрешность аппроксимации в пространстве образов оператора искажений:

^ = y - Ax ⁽ " ) ,                                     (14)

так как нам известен оператор искажений. Рис. 3 демонстрирует связь этих величин. Если бы x ^{( n )} являлось точным решением, то выполнялось бы равенство е = ^ = 0 . Иными словами, погрешности в пространстве образов и в пространстве прообразов оператора искажений имеют общий ноль.

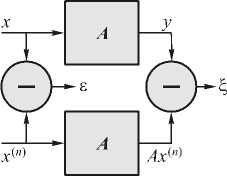
Рис. 3. Погрешность решения в пространстве сигнала и пространстве искажений

Из погрешности (14) и итерационной формулы (10) вытекает:

^ = y - Ax ⁽ n ) = x ⁽ n ^{+ 1)} - x ⁽ n ) .

То есть величина § может вычисляться как разность решений на двух последовательных итерациях. Поскольку сами погрешности (13) и (14) представляют собой случайные поля, для их характеристики на каждой итерации будем использовать их дисперсии е 2 и - .

В качестве критерия остановки итерационного процесса можно использовать:

• -    <А ,                                       (15)

где А - некоторый назначаемый порог.

Экспериментальное исследование

Экспериментальное исследование восстановления изображений при помощи описанной процедуры проводилось на модельных кусочно-постоянных квази-непрерывных изображениях, которые представляли собой набор мозаичных полей [4]. Мозаичное поле образуется при разбиении плоскости случайными прямыми и присвоении полученным областям случайных значений яркостей. Меняя среднее расстояние между линиями, можно обеспечить разный коэффициент корреляции изображений.

На рис. 4 а – пример неискажённого изображения, на рис. 4 б – результат восстановления предлагаемым методом. На рис. 4 в приведено отконтрастированное изображение погрешности восстановления. Рис. 4 г демонстрирует начальное приближение, которое значительно меньше соответствует исходному изображению, чем результат процедуры восстановления. Величина ошибки зависит от уровня коррелированно-сти изображения: чем меньше корреляция, т.е. меньше расстояние между объектами, тем ошибка выше.

При компьютерном моделировании оператора сглаживания использовалась дискретная свёртка. Пусть x ( m ₁, m ₂) – исходное квазинепрерывное изображение, h ( к 1 , k 2 ), - K < к 1 , k ₂ <  K - ИХ сглаживающего фильтра, тогда оператор A ₁ примет вид:

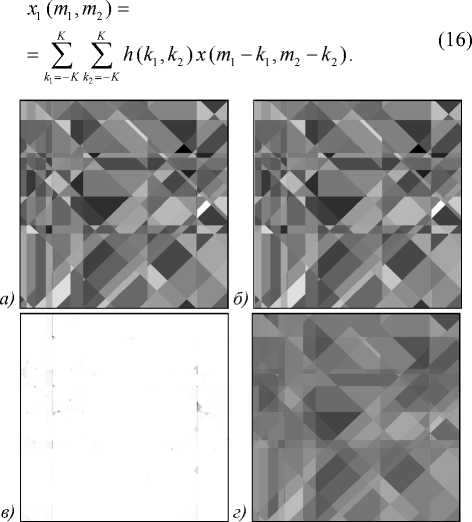
Рис. 4. Примеры изображений: а) квазинепрерывное мозаичное поле (коэффициент корреляции 0,95), б) результат восстановления, в) погрешность восстановления (после контрастирования), г) начальное приближение

В экспериментах применялись фильтры с гауссовой h ₁ импульсной характеристикой:

-

( ^к 12 ^{+ к} 22 )

,

2 R ²

h ( ^k i , ^к 2 ) = 0 exP

• -    K <  к 1 , к ₂ <  K ,

где Q ₁ – константа, обеспечивающая выполнение условия нормировки

Ki

ZZ hi (кi,к2) = 1, i = 1,2,(18)

• к i =- K к 2 =- K

и прямоугольной импульсной характеристикой h ₂

-------г, - K <  к , к ₂<  K

• h 2 (к1, к2 ) = ^( 2K +1)2                     .(19)

[ 0, иначе

В качестве пространственной дискретизации искажённого изображения x ₁ ( m ₁ , m ₂) использовалось равномерное прореживание в T раз. В качестве оператора A ₃ использовалась интерполяция по ближайшему соседу до уровня детализации исходного ква-зинепрерывного изображения.

В экспериментах с шумом использовался гауссов белый шум отношением шум/сигнал d = D V / D X , где D_X – дисперсия изображения, D_V – дисперсия шума.

Размер исходных неискажённых квазинепрерыв-ных изображений составлял 1024×1024 точки, параметр частоты прореживания составлял T = 8 , параметры гауссовой и прямоугольной импульсных харак- теристик определялись величинами K = 24, R = 8 и K = 8 соответственно. Эксперимент проводился на наборах по 10 изображений для трёх коэффициентов корреляции между соседними пикселами 0,9, 0,95 и 0,99.

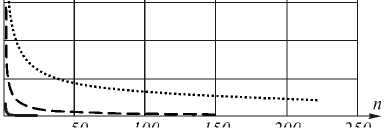
Рис. 5 а и рис. 5 б демонстрируют зависимость величины 8 2 / D X от номера итерации для случаев с гауссовой и прямоугольной импульсными характеристиками в отсутствие шума.

0,5

0,4

0,3

е2/ОЛ

—

...... р=0,90 -- р=0,95 --- р=0,99

—

0,2

0,1

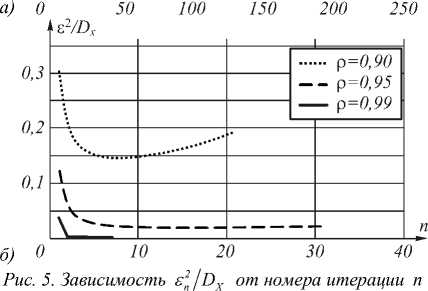
для случая с: a) гауссовой ИХ, б) прямоугольной ИХ, – при различных коэффициентах корреляции изображений

Итерационная процедура расходится в случае с прямоугольной импульсной характеристикой, поскольку не выполняется условие (8). Однако несмотря на расходимость, имеется минимум погрешности восстановления, в котором погрешность в несколько раз меньше, чем до применения итерационной процедуры. Т.е. данная процедура позволяет уточнить значения изображения в среднеквадратичном смысле, даже при отсутствии сходимости.

Исследования метода при наличии шумов проводились для значений d = 0,001; 0,01; 0,1 для всех изображений. На рис. 6 а изображены зависимости дисперсии погрешности восстановления от номера итерации для изображений с коэффициентом корреляции 0,95 и гауссовой искажающей импульсной характеристикой. При наличии шума погрешность восстановления имеет минимум, который хорошо прослеживается на графиках, что говорит об улучшении качества изображения.

Несмотря на отсутствие сходимости к точному решению при наличии шумов, итерационная процедура уменьшает погрешность восстанавливаемого изображения от 1,25 до 5 раз для изображений с корреляцией 0,9, от 2 до 15 раз при корреляции 0,95 и в 10 и более раз для корреляции 0,99.

Как видно из рис. 6а, оптимальное (в смысле погрешности) восстановление достигается относитель- но быстро, как правило, в течение первых двух десятков итераций. Поведение величины с 2 / DX при этих же условиях эксперимента представлено на рис. 6б.

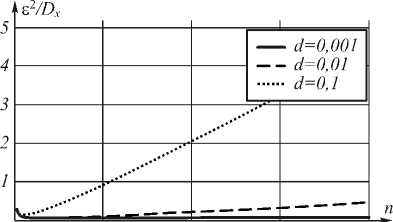
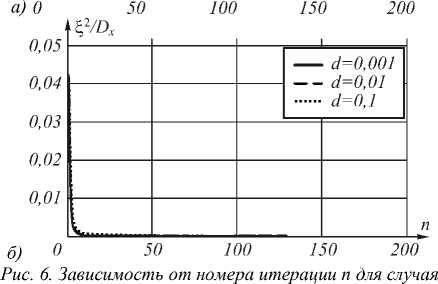
гауссовой ИХ, при значении коэффициента корреляции 0,95

и при отношении шум/сигнал d, равном 0,001, 0,01 и 0,1

Выводы

Описанная итерационная процедура повышает качество оценок изображений, близких к кусочнопостоянным, в широком диапазоне значений отношения сигнал-шум. Точность решения задачи восстановления ограничивается, во-первых, необходимой остановкой итерационного процесса, во-вторых, что более принципиально, наличием на изображении локальных «вставок» (объектов малой площади) среди протяжённых областей постоянной яркости.

Дальнейшее направление исследований связано с решением задачи выбора порога для остановки итерационных процедур Δ.

Работа выполнена при финансовой поддержке РФФИ (гранты 13-01-12080-офи и 13-07-97006-р_поволжье_а), программы фундаментальных исследований Президиума РАН «Фундаментальные проблемы информатики и информационных технологий» (проект 2.12), а также Минобрнауки РФ (госконтракт № 02.G36.31.0001 от 12.02.2013 г. в рамках Постановления Правительства РФ от 09.04.2010 г. № 218).