Итерационный расчет трибоконтакта ролика с пластиной
Автор: Иванов Виктор Андреевич, Еркаев Николай Васильевич
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 4 (56), 2014 года.
Бесплатный доступ
Разработана методика самосогласованного расчета контакта ролика с упругой пластиной конечных размеров при наличии смазочного слоя с учетом зависимости коэффициента вязкости от давления. Ключевым моментом является определение функций податливости, устанавливающих функциональную связь деформаций поверхностей ролика и пластины с давлением в смазочном слое. Для расчета функций податливости применяется известный программный комплекс ANSYS, основанный на методе конечных элементов, а также разложение Фурье. Для устранения вычислительных шумов типа мелкомасштабных осцилляций вводятся регуляризирующие множители для коэффициентов Фурье. Найденные функции податливости используются для самосогласованного расчета давления и прогиба поверхностей в зоне контакта по предложенной итерационной схеме. Представлены конкретные результаты расчетов давления и деформаций в области контакта ролика и пластины для различных нагрузок. Показана быстрая сходимость итераций. При этом необходимое число итераций зависит от нагрузки на ролик: возрастание максимального контактного давления приводит к увеличению числа итерационных циклов.
Итерации, контактное взаимодействие, смазочный слой
Короткий адрес: https://sciup.org/148177331
IDR: 148177331 | УДК: 628.822
Текст научной статьи Итерационный расчет трибоконтакта ролика с пластиной
Vestnik SibGAU
2014, No. 4(56), P. 48–54
ITERATIVE CALCULATION OF TRIBO-CONTACT BETWEEN A ROLLER AND A PLATE
-
V. A. Ivanov1, N. V. Erkaev2
1Polytechnic Institute of Siberian Federal University
-
26 , Kirenskiy st., Krasnoyarsk, 660074, Russian Federation. E-mail: VinTextrim@yandex.ru 2ICM SB RAS
50/44, Akademgorodok st., 660036, Krasnoyarsk, Russian Federation. E-mail: nerkaev@gmail.com
This article deals with the problem of the hydrodynamic contact of a roller with finite size elastic plate. The lubricant viscosity coefficient is assumed to be a function of the pressure. Generally, this problem requires joined solution of the 2-D hydrodynamic Reynolds’ equations and 3-D equations of solid mechanics. Our approach allows one to decouple the task of solid mechanics from the hydrodynamic task. At the first step, we solve the task of solid mechanics and find the compliance matrix, which establishes a functional relationship between surface deflections and pressure distributions along the lubricant layer. Determined ones, this matrix can be used for any pressure distributions along the lubrication layer. At the second step, we implement the obtained compliance matrix for solving the hydrodynamic problem. To find the compliance matrices, we apply the well known ANSYS package based on the finite element method, and also the Fourier series expansion. For suppressing the numerical noise-like small scaled oscillations we introduce regularization factors for the Fourier coefficients. The determined compliance matrices are used for self-consistent calculation of the pressure and surface deflections by the proposed iterative scheme. The particular results of calculations of pressure distributions and surface deformations are presented for different loadings. Fast convergence of the iterations is shown. Number of iterations depends on the loading conditions: An enhancement of the maximal contact pressure leads to increase of the number of the required iteration cycles.
Keyword: iterations, contact interaction, lubricant layer.
Введение. Расчет упругогидродинамического контакта ролика с деформируемой поверхностью является довольно сложной задачей, так как требует совместного решения уравнений гидродинамики в смазочном слое и уравнений упругости в деформируемом теле. Эта задача тесно связана с проблемой моделирования подшипников качения, которые широко используются во многих технических устройствах. Следует особо отметить применение подшипников качения в авиационных и ракетных двигателях, где они подвергаются предельным напряжениям. Большие силы и экстремальные температуры заставляют детали работать на пределе их технических возможностей. В то же время они должны отвечать самым строгим требованиям безопасности. Это накладывает повышенные требования к точности расчета рабочих характеристик конструктивных элементов подшипника. При этом корректный расчет деформаций рабочих поверхностей в присутствии смазки становится ключевой задачей.
Постановка задачи и подходы к решению обсуждались в работах [1–10], в которых рассматривался контакт ролика с упругим полупространством. В этих работах для расчета зоны контакта использовалось интегральное уравнение связи давления P и деформации 5 :
-
5 ( x ) = J P ( x ' ) K ( x - x ' ) dx ', (1) -to
где K ( x - x ') = K 1 ( x - x ') + K2( x - x) - суммарная функция податливости, характеризующая влияние давления в точке x ' на прогиб в точке x ; K 1 – функция податливости упругой пластины; K 2 – функция податливости ролика. В публикациях [2; 3] деформация ролика вообще не учитывалась ( K 2 = 0), а вместо пластины рассматривалось упругое полупространство, для которого функция податливости K 1 имеет простой аналитический вид:
2 ( 1 - m 2 ) ( 2£ )
K (x - x) = V 7 Ln — , (2) nE I |x - xH где m и E – коэффициент Пуассона и модуль упругости материала. Однако в реальном случае контакта ролика с пластиной конечной толщины функция податливости зависит от геометрических характеристик, и ее поведение не описывается простой логарифмической формулой (2). В этом случае отсутствуют аналитические выражения для функции податливости и необходимо привлекать численные методы решения задачи. Целью данной работы является построение метода численного определения функций податливости контактирующих поверхностей для случая контакта ролика конечной длины с упругим телом конечной толщины при наличии смазки. Для выполнения расчетов привлекается известный вычислительный комплекс ANSYS.
Описание метода расчета. Предлагаемый метод расчета может использоваться для проектирования подшипников качения. Так как радиус ролика очень мал по сравнению с радиусом кольца, по которому он катится, то можно приближенно принять внешнее кольцо подшипника плоской пластиной [7]. Для иллюстрации метода рассмотрим контактное взаимодействие цилиндрического ролика с движущейся пластиной, покрытой слоем смазочного материала (рис. 1). Весь ход решения задачи разбиваем на три этапа.
На первом этапе определяем распределение давления в смазочном слое из решения уравнения Рейнольдса:
d ( d P ) ( d h )
—I h exp( - a P )— 1 = 6ц V\ I , (3) d x | d x ) | d x )
где P – давление в смазочном слое; V – скорость движения пластины; ц 0 - динамическая вязкость масла при нормальном давлении; a - пьезокоэффициент давления [11]. Ось x ориентирована в направлении движения пластины.
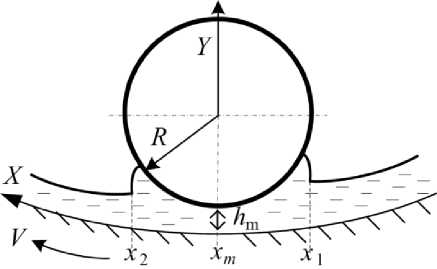
Рис. 1. Схема расположения ролика, пластины и слоя жидкого смазочного материала
Предполагая, что размер области контакта цилиндра и пластины мал по сравнению с радиусом ролика R , получаем следующее выражение для толщины слоя смазочного материала [2]:
h = h m + ( x - xm )2/ ( 2 R ) , (4)
где h m – минимальная толщина смазочного слоя; x m – координата точки минимального зазора. Формула (4), в которой пока не учтены упругие деформации поверхности, используется для предварительного расчета давления в области контакта. Деформации будут учтены в дальнейшем при выполнении итераций, описанных в последнем разделе.
Граничные условия в рассматриваемом случае имеют следующий вид [1; 2]:
dP
P ( x , ) = P ( x 2 ) = dP ( x 2 ) = 0,
где x 1 и x 2 – входная и выходная границы смазочного слоя.
Для удобства решения задачи вводим безразмерные переменные:
x = ( x - x m )/( hmR )1/2, q = Ph m /2/ ( 6 ц V4R ) , t = tV /( hmR )1/2.
После перехода к безразмерным переменным уравнение Рейнольдса (3) принимает более простой вид:
d ( / \ з d q ^ 8 H ( x )
— I H ( 5 c ) exp ( - a q )-^ I= V , (6)
dx | dx) dx где H(x) = 1 + x2 / 2; a = 6ац0V^R /h^'2.
Положения входной и выходной границ будем характеризовать безразмерными параметрами a и b :
( x i - x m ) , ( x 2 - x m )
a = b =
( Rhm ) ( Rhm )
Значение параметра a зависит от количества смазки. В случае обильной смазки полагают a = –∞ [2–4].
Интегрируя уравнение (6) и используя нулевое граничное условие (5) для производной функции давления при x = x 2, получаем дифференциальное уравнение первого порядка:
и интегрируем от –l / 2 до l / 2. В результате получаем систему линейных алгебраических уравнений относительно неизвестных коэффициентов M k и N k :
. дq H(x)-H(b) (x2 -b2)/2 exp(-a q) — = ——--—= -----—r дX H (X )3 (1 + X 2/2)3
—^
.
В результате интегрирования уравнения (7) находим функцию, характеризующую распределение давления в смазочном слое и зависящую от параметра b :
l /2
M k j P ( x ') sin I k — x ' I dx ' +
-l/2 A l v l/2
dx ' =
1 - exp( - a q ( x ))
α
arctan
x
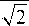
n)V2( 3, A
+ 1 b 2 -
2J 4 ( 2 J
- 1 /2
l /2
= 2 f 5 sin I k
I
1 -1/2 A l/2
', k * 0,
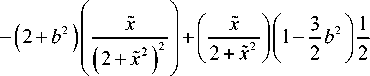
l /2
l /2
dx ' -
dx ' =
Неизвестный параметр b определяем с помощью граничного условия q ( b ) = 0, из которого следует трансцендентное уравнение
- l /2
l /2
— x ' |- dx ', k * 0;
I b I п I \ 2 I _ 3 ,2 1 7 2 \ arctan —;= + — — 1 —b - 2 + b x
( V2 J 2 J 4 ( 2 J v
x
b
U 2 + b 2)’
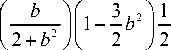
-1/2 v 1 v l/2 l/2
M 0 j P ( x ') dx' = - j 5 - dx '.
- 1 /2 l - 1 /2
Решая систему линейных алгебраических уравнений (11), находим коэффициенты Фурье:
Решая уравнение (9) численно методом Ньютона, находим значение искомого параметра: b = 0,67155. Подставляя найденное значение b в уравнение (8), получаем распределение давления в смазочном слое, удовлетворяющее всем граничным условиям.
На втором этапе найденное распределение давления используем для определения прогиба упругой поверхности, контактирующей с роликом, и деформации самого ролика. Для этого применяем программный комплекс ANSYS, основанный на методе конечных элементов [12]. В нем строится модель пластины и ролика, которые разбиваются сеткой на элементарные конечные элементы. При разбиении на элементы необходимо учитывать, что в зоне контакта сетка должна быть строго упорядоченной и достаточно мелкой для более точного расчета. На граничных узлах сетки в области контакта задается найденное на первом этапе распределение давления. Далее выполняется расчет в ANSYS, после которого снимаются показания прогибов контактирующих поверхностей, которые используются в дальнейшем для определения функции податливости.
На третьем этапе определяем функции прогибов на основе результатов расчета ANSYS и интегральной формулы (1). Для искомых функций податливости используем разложение Фурье следующего вида:
n
K(x )_E i=0
Mi cos
где l – интервал изменения функции податливости (порядка длины контакта).
Подставляем выражение (10) в уравнение (1),
I 2n A ■ ( 2n ,)
умножаем поочередно на cos I x—k I и sin I x—k I
M
r л k^k ~ kk^k k"l X2 + Y
N = 2 YC - XD , k l X k + Y/
, k * 0 ,
M _ 1 X 0 C 0 + Y 0 D 0 N _ 1 Y 0 C 0 - X 0 D 0
0 l X 0 + Y 2 ’ k l X 0 + Y 0 ,
где
l /2
I 2n 1
Yk = P ( x )cos I k — x I- dx ,
-
-1/2 A 12
l /2
I
Xk = I P ( x )sin I k — x I- dx ,
-
-1/2
l /2
- l /2
l /2
l /2
Здесь функции P ( x ) и 5 ( x ) определяются сплайн-интерполяцией сеточных значений P i и 5 i . Важно отметить, что при восстановлении функции податливости возникают шумы, связанные с влиянием мелкомасштабных погрешностей в исходных данных, полученных на основе расчета ANSYS. Чтобы устранить эти шумы, необходимо использовать специальную регуляризацию. Общая теория регуляризаций при решении интегральных уравнений описана в монографии [13]. Для подавления шумов вводим регуляри-1
зирующие множители вида g. =------, где £ - ма- j 1 + s j 4
лый параметр, подбираемый для уменьшения паразитных осцилляций. В этом случае выражения (12) принимают вид
- =2 XkCk + YkDk ~ =2 YkCk - XkDk k l Xk2 + Yk2 gk, k l X2 + Yk2
g k , k * °;
M = 1 X 0 C 0 + y 0 D6 N = 1 У C 0 - X 0 D o
0 l X 02 + У 2 , 0 l X 02 + У 2
Подставляя найденные значения Mk и Nk из (13) в формулу (10), получаем сглаженную функцию податливости:
n
K (x )=Z k=0
( 2n , ) ( 2n,
Mk cos I x — k \ + Nk sin I x~k
Формула (14) применима как для K 1 – функции податливости упругой пластины, так и для K 2 – функции податливости ролика. Функции K 1 и K 2 могут существенно отличаться в силу различий геометрических характеристик и свойств материалов пластины и ролика.
На последнем этапе используем найденную функцию податливости для уточненного расчета распределений давления и прогиба итерационным способом. Итерационная формула имеет вид
H 0 ( 5c ) = 1 + x 2 /2,
b
5 ( n ) ( x ) = A J q n ( x ' ) K , ( в ( x - x ') ) dx ', a
b
5(2 n ) ( x ) = A J q n ( x ' ) K 2 ( в ( x - x ') ) dx ',
a
Hn ( x ) = 1 + x 2 / 2 + 3 ( n - 1) ( x) + 5 2 n - 1) ( x) =
b
= 1 + x 2 /2 + A J q n - 1 ( x ' ) K 1 ( в( x - x ') ) dx ' + a
b
+ A J Q n - 1 ( x ' ) K 2 ( в( 5е - x ') ) dx , a
1 - exp ( - a Q n ( x )) = Г H n ( x ,) - H n ( b ) d x '
a J H n ( x ') 3 , (15)
n = 0, 1, 2, 3.., где n - номер итерации; p = (R hm )1/2/Ly; A = 6 Цо V R /hm2 — коэффициенты, вычисляемые по заданным параметрам задачи; Ly – толщина пластины.
На нулевой итерации расчет давления в смазочном слое выполняется без учета прогиба упругого слоя. В процессе сходящихся итераций получаем самосогласованные распределения давления и прогиба в области контакта.
Иллюстрация метода на конкретном примере. Для расчетов использовались следующие числовые параметры: h m = 0,00001 м, ц = 0,024 Пат, V = 7 м/с, R = 0,005 м (за основу взят подшипник 32114 серии [14]). Для моделирования примем, что материалы пластины и ролика идентичны и имеют следующие механические свойства: E = 2,1·1011 Па – модуль упругости (сталь), m = 0,3 – коэффициент Пуассона.
Решая уравнение (9) численно методом Ньютона, находим b = 0,67155. Подставляя найденное значение b в уравнение (8), получаем распределение давления, показанное на рис. 2. Далее найденное распределение давления используем для определения прогибов упругой поверхности и ролика.
. (14)
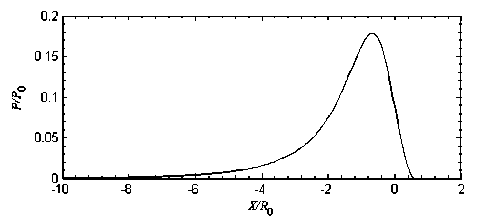
Рис. 2. Распределение безразмерного давления в смазочном слое при отсутствии упругих деформаций. Координата нормирована к характерному размеру зоны контакта R 0 = ( R hm )1/2
В программном комплексе ANSYS для моделирования процесса контакта была построена расчетная модель упругой пластины (упругий параллелепипед размерами L x × L y × L z = 0,2 × 0,05 × 0,2 м). Вся расчетная область разбивалась на 40 элементов по длине, 10 элементов по высоте и 4 элемента по ширине (крупная сетка). В зоне действия нагрузки делалось дополнительное, более мелкое разбиение области на 90 ячеек вдоль пятна контакта для большей точности расчетов (рис. 3, а ). Внутри упругого ролика ( R = 0,005 м) расчетная область от R = 0 м, до R = 0,002 м разбивалась свободной сеткой, предложенной комплексом ANSYS. Область от R = 0,002 м, до R = 0,005 м разбита на 10 элементов. Расчетная область, за исключением пятна контакта, разбита на 40 элементов по длине окружности, а само пятно контакта дополнительно разбито на 90 элементов (рис. 3, б ).
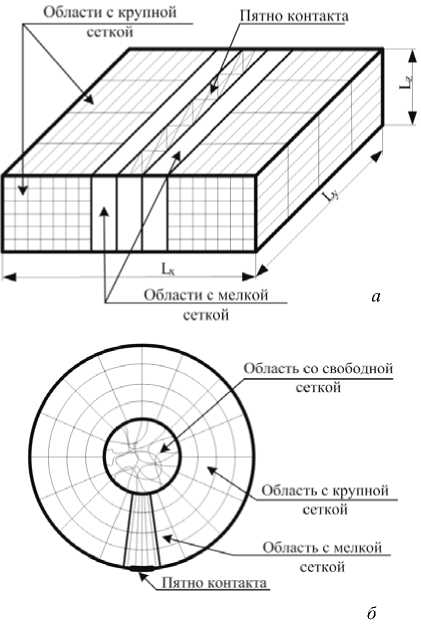
Рис. 3. Схема расчетной сетки, используемой в ANSYS: а – для упругой пластины; б – для упругого ролика
В качестве нагрузки задавалось давление, действующее на каждую ячейку сетки вдоль пятна контакта. Выполняя расчет ANSYS для заданного распределения давления (рис. 2), получаем значения деформаций ролика и пластины, показанные на рис. 4.
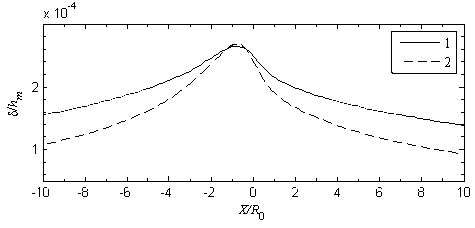
Рис. 4. Прогиб поверхности, полученный в результате моделирования в ANSYS: 1 – упругой пластины; 2 – упругого ролика
Используя найденное ранее распределение давления в слое и рассчитанные по программе ANSYS деформации, определяем из решения системы (12) коэффициенты Фурье.
Для сглаживания паразитных осцилляций вводим регуляризирующие множители. Осцилляции сильнее проявляются на краях и в меньшей степени – в центральной части области определения функции податливости. Поэтому в центральной части применяем множители g 1 k с меньшим сглаживанием, а на периферии – множители g 2 k с большим сглаживанием:
g 1 n 1 + 0,0002 n4’ g 2 n 1 + 0,0008 n4'
Подставляя найденные значения Mk и Nk с множителями (16) в формулу (14), получаем окончательное выражение функции податливости в виде n z k=0
( 2n , Y „ • ( 2n
M k g i k cos I x y k I+ N kg i k sin I x—
K ( x ) Y
|x / L\ < 0,03;
n
k = 0
E " I 2n
M k g 2 k cos I x —
,) „ • ( 2n ,)
k I + Nkg 2 k sin I x—k I ,
I x / L > 0,03.
График найденных функций показан на рис. 5. Значения функций нормированы к их максимальным значениям: Kmax1 = 3,267·10–15 Па–1 для упругой пластины и Kmax2 = 3,45·10–15 Па–1 для упругого ролика. Пики функций податливости пластины и ролика очень близки по значениям. Это объясняется идентичностью механических свойств материалов ролика и пластины. При этом функция податливости пласти- ны существенно медленнее спадает по сравнению с функцией податливости ролика, что связано с различием их геометрических параметров. Характер убывания функции податливости для ролика зависит от его радиуса, а для пластины – от её толщины.
Полученная формула (14) для функции податливости может применяться при любых распределениях давления в смазочном слое для заданных размеров пластины и ролика. Проверка данного метода выполнена в [15].
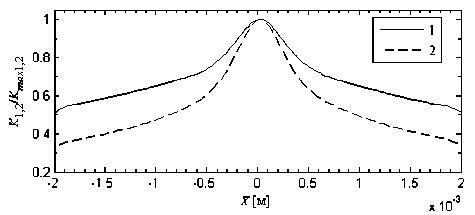
Рис. 5. График функций податливости: 1 – упругой пластины; 2 – упругого ролика
Далее включаем найденные функции податливости в общую итерационную схему для самосогласованного расчета давления и прогиба в зоне контакта. Сначала выполняем расчет для h m = 0,000001 м. Результаты расчетов прогиба и давления представлены в таблице. Нулевая итерация не учитывает прогиб поверхности и поэтому дает наибольший пик давления. При следующих итерациях, учитывающих прогиб, пик давления заметно снижается. Как видно из таблицы, установившийся режим для данного случая наступает уже на третьем итерационном шаге. На дальнейших итерационных шагах относительные изменения максимального прогиба и давления очень малы (составляют сотые доли процента).
Таблица
Максимальные значения давления и прогиба для h m = 0,000001 м
|
№ итерации |
Давление P· 107 Па |
Прогиб δ·10–8 м |
Нагрузка 103, Н |
|
|
Кольцо |
Ролик |
|||
|
0 |
1,33280 |
2,88508651 |
2,98079148 |
4,871 |
|
1 |
1,2209 |
2,715387 |
2,804656146 |
4,499 |
|
2 |
1,2272 |
2,725262225 |
2,8149000698 |
4,522 |
|
3 |
1,2268 |
2,7244631096 |
2,8140732702 |
4,52 |
|
4 |
1,2269 |
2,7250222903 |
2,8146484524 |
4,522 |
|
5 |
1,22687 |
2,7247243298 |
2,8143419046 |
4,521 |
Далее проводим серию вычислительных экспериментов, постепенно увеличивая давление за счет уменьшения минимального зазора. Так, выполняем расчеты для следующих значений минимального зазора h m : 0,00000085, 0,00000065, 0,0000005, 0,00000037 и 0,00000025. Расчеты показали, что уменьшение параметра h m (увеличение внешней нагрузки) приводит к некоторому замедлению сходимости процесса и увеличению числа итерационных шагов для достижения требуемой точности. На рис. 6 показана зависимость минимального зазора в смазочном слое от контактной нагрузки. Зависимость нагрузки от распределения контактного давления определяется следующим интегральным уравнением:
W = J P ( x ) dx , (17)
x 1
где W – контактная нагрузка.
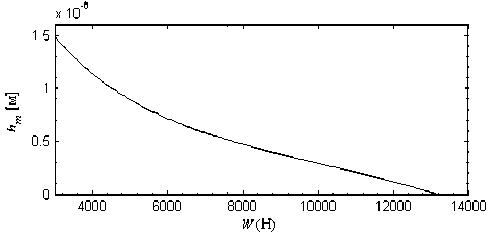
Рис. 6. Зависимость минимального зазора в смазочном слое hm от контактной нагрузки W (17)
Заключение. Разработан подход к решению задачи упругогидродинамического контакта ролика с движущейся пластиной конечной толщины. На первом этапе на основе решения уравнения Рейнольдса выполняется предварительный расчет давления в смазочном слое без учета деформаций поверхности. Далее распределение этого давления задается в программе ANSYS для определения упругих деформаций пластины и ролика. В предположении линейной интегральной связи деформации и давления определяется функции податливости контактирующих тел. Найденные функции податливости не зависят от конкретного распределения давления в смазочном слое и используются для итерационного расчета характеристик смазочного слоя и деформаций поверхностей при различных нагрузках.
Список литературы Итерационный расчет трибоконтакта ролика с пластиной
- Коднир Д. С. Контактная гидродинамика смазки деталей машин. М.: Машиностроение, 1976. 304 с.
- Галахов М. А., Усов П. П. Дифференциальные и интегральные уравнения математической модели теории трения. М.: Наука. Физ.-мат. лит., 1990, 280 с.
- Галахов М. А., Гусятников П. Б., Новиков А. П. Математические модели контактной гидродинамики. М.: Наука, 1985, 294 с.
- Терентьев В. Ф., Еркаев Н. В., Докшанин С. Г. Трибонадежность подшипниковых узлов в присутствии модифицированных смазочных композиций. Новосибирск: Наука, 2003, 142 с.
- Venner C. H., Lubrecht A. A. MultiLevel methods in lubrication. Amsterdam: Elsevier, 2000. P. 400.
- Venner C. H. Multilevel solution of the EHL line and point contact problems/PhD thesis, University of Twente. Endschende, 1991.
- Venner C. H., Lubrecht A. A. Numerical simulation of a transverse ridge in a circular EHL contact under rolling sliding//Trans. ASME J. Tribol. 1994. Pp. 751-761.
- Anuradha P., Kumar P. EHL line contact central and minimum film thickness equations for lubricants with linear piezoviscous behavior//Tribol. 2011. Int. 44. Pp. 1257-1260.
- Беспорточный А. И. Асимптотические режимы гидродинамического контакта упругого цилиндра и жесткого полупространства//Труды МФТИ. 2013. Т. 5, № 2. С. 4-12.
- Беспорточный А. И. Режимы смазки контакта цилиндра с упругим покрытием и жесткого полупространства//Научный вестник МГТУ ГА. 2011. № 163. С. 138-143.
- D’Agostino V., Petrone V., Senatore A. Effects of the lubricant piezo-viscous properties on EHL line and point contact problems//Tribol. Lett. 2013. Int 49. Pp. 385-396. DOI 10.1007/s11249-012-0079-5.
- Любимов А. К. Применение системы ANSYS к решению задач механики сплошной среды. Нижний Новгород: Изд-во Нижегородского гос. ун-та. 2006. 227 с.
- Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач. М.: Наука. 1979. 288 с.
- Нарышкин В. Н., Коросташевский Р. В. Подшипники качения. Справочник-каталог. М.: Машиностроение, 1984. 280 с.
- Иванов В. А., Еркаев Н. В. Моделирование контакта ролика с пластиной при наличии смазки//Технология машиностроения. 2014. № 6. C. 53-58.


