Итеративное оценивание с использованием информации об эмпирических распределениях невязок

При решении задач оценивания по малому числу наблюдений распределения ошибок на отдельных реализациях не обладают статистической устойчивостью, поэтому использование априорных вероятностных моделей помех не вполне правомерно. Если о распределении ошибок ничего не известно, то, опираясь на восходящее к Гауссу мнение, применяют метод наименьших квадратов (МНК). Однако известно, что если распределение ошибок на конкретных реализациях существенно отличается от гауссовского, МНК-оценки, оказываются неработоспособными [1].

Для преодоления указанного недостатка строят так называемые робастные оценки в расчете на "наихудшее" (например, в смысле фишеровской информации) распределение из некоторого класса [2]. Такой подход обеспечивает повышение надежности оценок, однако возможна существенная потеря точности по сравнению с классическими МНК-оценками в ситуациях, когда распределение ошибок на конкретной реализации в действительности оказывается близким к гауссовскому.

Более адекватным существу задачи в данном случае представляется адаптивный подход, заключающийся в подборе наиболее подходящей модели ошибок для каждой реализации в ходе оценивания. Центральной проблемой при этом является получение необходимой для реализации процедуры перестройки дополнительной информации. Такая информация может быть получена, напри мер, путем дополнительных измерений [3]. В настоящей работе исследуется возможность получения дополнительной информации путем изучения распределений реализаций вектора невязок, получаемых на промежуточных шагах так называемого итерационного МНК [4].

Постановка задачи

Рассматривается задача оценивания M x 1-вектора c параметров модели типа линейной регрессии:

у = Xc + о , (1)

где N x M- матрица X = [ x 1 , x ₂ ,._ x N , J и N x 1-вектор у составлены из доступных для наблюдения измерений, а - неизвестный N x 1-вектор ошибок. Предполагается, что N мало (превышает M не более чем в 2-3 раза).

Для получения оценок реализуется схема итерационного МНК в виде следующей последовательности шагов. Вычисляются начальная МНК-оценка c = [xtx ] X у (2) вектора параметров с модели (1) и вектор невязок о= у - Xc.            (3)

Далее по вектору невязок строится так называемая весовая матрица

G = G £) = diagg 1 ,g₂ ,..g_N ) , осуществляется преобразование исходных данных:

X = GX, у = Gy ,         (4)

и вновь вычисляется МНК-оценка (2) по X и у .

Если в рамках этой схемы весовые коэффициенты g i , i=1, N на каждом шаге процедуры (2)-(4) вычисляются по правилу g i = | X i| ^v 2 , 0 <  v <  2 , она совпадает с итерационным МНК, предложенным в работе [5] для вычисления L _v - оценок. К этой же схеме можно свести вычисление оценок максимального правдоподобия параметров сдвига c и масштаба s плотности p ( ^ ( c ), s ) .

Действительно, пусть функция потерь

F (^(c),s)=- lrp(5(c),s)       (5)

удовлетворяет условиям:

Fx'(x(c),s)x-1 > 0 limg(x,s) = 0, [• x ., ling(X,s) < ¥

X ®o где g £,s) = (F ^(c)^ ~1 )12 •

Тогда искомые оценки c , ' :

N

Q ⁽ X ⁽ c) s ) = min £ F ( £ ( c ) s ) ^c,s i = 1

являются решением системы (M+1) уравнений вида

N

Ё g^{2 ( X} ( c ), sk x r

i = 1

c -

Ё g^{2 ( X} ('''к Y i

. i=1

= 0 ,

N

Ё ^F s' ( ^ i ^{( c} X^s' ) = ⁰ •           (9)

i = 1

Попеременное решение уравнений (8) и (9), по существу, является схемой последовательных МНК-оценок (2)-(4). В частности, решение уравнения (8) доставляет взвешенные МНК-оценки, а элементы весовой матрицы могут быть вычислены по соотношению (7) при s = ', которое является решением нелинейного уравнения (9). Формальное совпадение вычислительных схем послу жило поводом для вывода о том, что оценивание методом взвешивания (2)-(4) на одном малом наборе данных согласуется со статистической теорией оценивания [3, стр.244]. Необходимо подчеркнуть, что такое сходство носит исключительно внешний характер.

Таким образом, весовая матрица преобразования G может быть построена, если задана априорная гипотеза о виде плотности распределения вероятности вектора ошибок. Поскольку априорное распределение вектора ошибок никогда не известно, поставим следующую задачу.

Зададим совокупность гипотез в виде n функций распределения

• ^{{ F} 1 ⁽ Х >^2 (M .^F n Й ,. )}

или плотностей

• ^{ Р 1 ^{X ,}4p fe ^,s )z ..,p n ⁽ ^ ^,s )} ,     ⁽¹⁰⁾

где £ - вектор невязок (3), а s - неизвестный параметр (масштаба). Будем на каждой очередной итерации алгоритма решать задачу выбора наиболее правдоподобной гипотезы относительно эмпирического распределения вектора невязок. Далее с использованием выбранной функции p(х (c),s) по указанным выше соотношениям вычисляются весовые коэффициенты g X ,s) и строится оценка вектора параметров на следующей итерации.

В рамках этой постановки задачи возникают, по крайней мере, две проблемы. Во-первых, в какой мере в рамках указанной выше вычислительной схемы правомерно использовать гипотезу p(x (c),s) вместо неизвестной плотности p(X (c)^s) для вычисления весовых коэффициентов. В качестве обоснования такой "подмены" можно привести следующие соображения. Можно показать, что £ = Т0 Т £, где T0 - Nx(N-M) - матрица, составленная из нормированных собственных векторов, соответствующих нулевым собственным значениям матрицы XXT. Из этого равенства видно, что если вектор ошибок принадлежит нуль-пространству матрицы XT, он совпадает с вектором невязок. Есть осно- вания полагать, что в некоторой окрестности нуль-пространства всегда существует множество векторов ошибок достаточно близких к соответствующим векторам невязок. Для этого должны выполняться обычные требования слабой сопряженности векторов ошибок и полезных сигналов (столбцов матрицы X). Признаком принадлежности вектора ошибок окрестности нуль-пространства может служить сравнительное большое (при соответствующей нормировке) значение нормы вектора невязок.

Вторая проблема связана с применением в данном случае классических критериев проверки гипотез при малом числе наблюдений. Деликатность ситуации состоит в том, что даже в случае, когда ошибки независимы и одинаково распределены, невязки являются зависимыми и неодинаково распределенными. Поэтому на вектор наблюдений (невязок) следует смотреть как на реализацию некоторого случайного процесса, а не как на выборку в классическом смысле.

В настоящей работе предлагаются некоторые эмпирические критерии принятия решений о наиболее правдоподобном семействе функций распределения (плотностей) для вычисления весовых коэффициентов с использованием компонент вектора невязок. При этом не принимается во внимание в полной мере существование отмеченной выше второй проблемы и предлагаемые критерии во многом аналогичны классическим. Учитывая этот факт, проводится сравнительный анализ критериев и экспериментально показывается, в какой степени информация об эмпирическом распределении невязок является полезной и может быть использована для повышения точности оценок.

Критерии выбора наиболее правдоподобной гипотезы

В качестве набора гипотез (10) рассмотрим симметричные относительно оси ординат параметрические семейства функций, удовлетворяющих условиям (5)-(7) и зависящих (при ^ ₀ =0) лишь от одного параметра масштаба s.

Среднеквадратичный критерий.

В качестве меры для различения гипо тез о принадлежности эмпирической функции распределения f ^ ^) к одному из заданных однопараметрических семейств F j ^,s) будем рассматривать критерий вида:

+^г ъ

J j s) = J [ F j ^ ,s) - F . g ) J d ^ . (11) —TO

Наиболее правдоподобной считается та гипотеза, для которой величина критерия (11) является наибольшей.

Критерий нормированного квантиля

Для набора априорных вероятностных моделей (гипотез) (10) наряду с (11) будем рассматривать критерии различения, основанные на непосредственном вычислении характеристик эмпирического распределения.

Зададимся некоторой вероятностью p₀. Квантиль, соответствующий данной вероятности, зависит от вида функции распределения и пропорционален параметру масштаба s или с.к.о. о (если оно существует). Поэтому произвести выбор можно по величине K q,j = F j ^{- 1} (p₀)/ о . В данном случае по выборке вычисляется эмпирическое значение этой величины и сравнивается с теоретическими значениями для заданных распределений. Выбирается то распределение, у которого K q j наиболее близко к эмпирическому.

Критерий нормированного среднего модулей невязок.

Смысл критерия поясним на рисунке 1, где приведена непрерывная функция распределения F( £ ). В данном случае в качестве признака принадлежности эмпирического распределения к одному из заданных априорных семейств используются величины площадей, в областях слева и справа относительно центра. На рисунке, эти области обозначены S и заштрихованы.

Можно показать, что суммарная (слева и справа от ординаты) площадь равна математическому ожиданию модуля величины £ . Этот факт очень важен при практическом использовании, так как позволяет избежать построения вариационного ряда и эмпирической функции распределения. Данная площадь имеет ту же размерность, что и сама

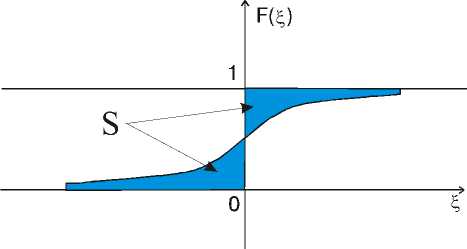
Рис. Непрерывная функция распределения F ( X )

случайная величина. Сравнение распределений производится по безразмерным величинам, также как в случае критерия нормированного квантиля.

Будем рассматривать два способа нормировки среднего модулей невязок:

• а)    Нормировка на среднеквадратичное отклонение В этом способе величиной для сравнения распределений является S / ст .

• б)    Нормировка на площадь равномерного распределения.

В этом способе уже при теоретическом рассмотрении непрерывного распределения используются не бесконечные, а конечные пределы интегрирования - минимальное и максимальное значения невязок Е и Е . min max

Нормировка производится на площадь, заключенную под функцией распределения равномерной плотности в тех же пределах. Сравнение распределений производится так же, как и в предыдущем способе. Далее приводятся результаты сравнительного исследования эффективности описанных критериев.

Проверка гипотез и процедура оценивания с использованием среднеквадратического критерия

В таблице 1 приведены некоторые из известных симметричных относительно центра параметрических семейств распределений, удовлетворяющих условиям (5)-(7) [6]. Для упрощения рассматриваются функции, зависящие лишь от одного параметра масштаба - s. Во втором столбце приведены выражения для функций функции p (< E ( c ), s ) , в третьем - соответствующие им функции потерь (5), а в четвертом - выражения для квадратов весовых коэффициентов (7).

Прежде всего, проиллюстрируем принципиальную работоспособностьсреднеквад-ратического критерия (11), который в дискретном случае можно переписать в виде гn -112

Jj Ы = № S^)-Pi I * С - Ei)^

L i=1

Здесь E - отсчеты вариационного ряда, построенного из компонент вектора невязок

^Е , ⁿ е K i & J

pi - отсчеты эмпирической функции распределения F j Е ,s) i = 1,N •

Заметим, что "весовые" множители E _{i + 1} - E i по смыслу близки к множителям n / p i при вычислении статистики %² (если N - число разрядов, а n - объем выборки). При малом числе наблюдений использование свойств %² -распределения, конечно, необоснованно. Более того, теряет смысл и раз-

Таблица 1. Параметрические семейства распределений

	ТуНКЦИЯ p( x ( c ) , s )	Т ункция потерь	Тункция g ( X ,s )
1	-^ ___1___ e 2 s 2 s V2P	ln(V2 ps ) + (-V^s 2 )	1 I2
2	i     1X J 47(1+7)e s	ln4 s + x /s - In ( 1 + x /s )	1 s ( s + x )
3	s        1 — *——— p s 2 +X 2	In ( s 2 ■ X 2 ) + ln ( p/s )	2 2 , £2 s +X

биение выборки на разряды, поэтому мы полагаем N=n. Однако указанная аналогия может быть полезна при необходимости верификации результатов при больших N.

Для проверки эффективности критерия (12) проводился эксперимент, заключавшийся в генерации малых выборок с заданными в таблице 1 законами распределения и последующей их аппроксимацией набором тех же параметрических семейств функций. При построении набора данных в качестве случайного значения ^i принимался квантиль, соответствующий вероятности i — 0,5 . :

Pi =------- , i = 1,N .

i N

При этом способе построения выборки длина отрезка интегрирования [a;b] растёт с ростом N как ~ V lrN при распределении 1, ~ lnN при распределении 2 и ~ N при распределении 3. Поэтому оценка сверху погрешности традиционных квадратурных формул может не выполняться. Тем не менее, отношение (b-a)/Nдля распределений 1 и 2 стремится к нулю, поэтому выражение под корнем в правой части (12) является интегральной суммой для интеграла (11). При этом вместо кажущегося естественным выбора n i по формуле центральных прямоугольников: П = С + ^ i ₊ i )/2 , ^ве™^чины zf i e fe i ^ i +J определялись равными квантилям соответствующих вероятностей:

i

Рн =-- , i = 1,N - 1 .

1 N

Это позволяет исключить методическую ошибку аппроксимации и, в частности, обеспечивает равенство нулю критерия (12) в случае, когда генерируемое и аппроксимирующее семейства совпадают.

Аппроксимация построенных для каждого набора данных эмпирических функций распределения осуществлялась по принципу "каждая" "каждой". Для оценки параметра масштаба s методом дихотомии решалось уравнение djjs)ds = 0 . Результаты исследования для N=25 приведены в таблице 2. Целые числа 1-3 в обозначениях строк и столбцов соответствуют номерам исходных распределений в таблице 1. При дальнейшем увеличении N они практически не изменяются.

Результаты моделирования подтверждают предположение о возможности непосредственного использования критерия (12) для оценки априорных гипотез при небольших N (N <  25). Значение критерия при аппроксимации множества компонент вектора невязок "своим" параметрическим семейством действительно минимально и отличается от нуля, по-видимому, лишь из-за погрешностей округления.

Исследовалась также частость совпадений параметрических семейств распределений компонент векторов ошибок и невязок. Эксперимент проводился по следующей схеме. Осуществлялось оценивание вектора c параметров уравнения (1) по матрице X и вектору у в присутствии вектора ошибок £ . Размерности векторов у и ^ 25 x 1. Генерировалось по 100 реализаций вектора выхода модели и шума указанной длины для каждого заданного параметрического семейства распределений. После получения оценки c для каждой реализации вычислялся вектор невязок (10) и строилась эмпирическая функция распределения его компонент. Затем она аппроксимировалась каждым из указанных выше трех (1, 2 и 3) параметрических семейств распределений и подсчитывалось значение критерия (12). При моделировании

Таблица 2. Результаты исследования эффективности критерия (12) для N=25

Вид	1		2		3
распределения	s	J ä (s)	s	J ä (s)	s	J ä (s)
1 (s=1,000)	1,000	0,00011	0,554	0,02213	0,543	0,07834
2 (s=0,546)	1,071	0,03682	0,546	0,00020	0,510	0,06869
3 (s=0,480)	1,665	0,21448	0,578	0,14051	0,480	0,00005

Таблица 3. Относительное число совпадений распределений ошибок и невязок

Распр еделе ние Априо рная гипоте за Относительн ое число решений Кср (в %) Средняя норма вектора невязок 1 1 54,3 4,439 2 43,4 4,405 3 2,3 3,578 2 1 28,2 4,614 2 66,4 4,753 3 5,4 4,555 3 1 0,4 2,236 2 26,1 9,843 3 73,5 10,747 векторов ошибок искусственно вводилась рандомизация, а результаты усреднялись по 100 экспериментам. В таблице 3 приведены данные об относительном числе случаев K ср , в которых каждое распределение оказывалось наилучшей, в смысле минимума критерия (12), аппроксимацией.

Приведенные данные хорошо согласуются с высказанными ранее соображениями качественного характера о том, что значение нормы вектора невязок свидетельствует о близости его распределения к распределению вектора ошибок. Приведем теперь результаты оценивания вектора параметров.

Эксперимент проводился для той же модели и при тех же размерностях векторов, как и выше. Особенность эксперимента заключалась в следующем. Параметрические классы распределений, задаваемые на этапе моделирования, считались известными, а оценивание осуществлялось по трехшаговой схеме с использованием весовых коэффициентов, соответствующих классам 1-3 из таблицы 1. Для анализа вектора невязок и принятия решения о типе преобразования взвешивания использовался среднеквадратический критерий. Вычислялись средние (по 100 реализациям) погрешности оценок вектора параметров с, на первом - £1 и третьем - £3 шагах процедуры оценивания в процентах. Результаты приведены в таблице 4.

Указанный в таблице выбор значений параметра s связан с тем, что при аппроксимации функции распределения (см. таблицу 2) оптимальное значение s для распределений 2 и 3 примерно вдвое меньше, чем для распределения 1 (при аппроксимации по методу моментов для распределения 2 значение s будет точно в два раза меньше). Приведенные результаты подтверждают принципиальную возможность существенного повышения точности при использовании стратегии МНК-оценивания при малом числе наблюдений.

Описанный метод проверки гипотез по среднеквадратическому критерию обладает существенным недостатком - очень большим

Таблица 4. Погрешности на первой и третьей итерации трёхшаговой схемы оценивания

Исходное распределение 1
s	0,01	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
6 1	0,2374	2,458	4,646	7,736	9,131	12,88	14,66	19,75	22,52	21,54	21,57
6 3	0,2374	2,458	4,646	7,736	9,131	12,88	14,66	19,75	22,52	21,54	21,57
Исходное распределение 2
s	0,01	0,05	0,1	0,15	0,2	0,25	0,3	0,35	0,4	0,45	0,5
6 1	0,4982	2,509	4,443	8,065	9,717	14,39	13,64	15,48	18,58	27,58	26,22
6 3	0,5111	2,568	4,194	7,707	9,645	14,58	13,30	15,05	18,34	25,78	26,05
Исходное распределение 3
s	0,01	0,05	0,1	0,15	0,2	0,25	0,3	0,35	0,4	0,45	0,5
6 1	1,395	5,480	10,94	21,62	22,62	29,21	38,57	45,82	50,85	56,12	68,07
6 3	0,723	2,987	6,73	11,04	12,49	15,48	21,74	23,83	27,68	27,44	28,85

объёмом вычислений. Эксперименты показывают, что на определение вида распределения затрачивается примерно в 4,4 раза больше времени, чем на все остальные вычисления. Далее приводятся результаты исследования других, предложенных в разделе 2 критериев, основанных на непосредственном вычислении характеристик эмпирического распределения.

Проверка гипотез по критерию нормированного квантиля

Прежде чем вести речь о других критериях проверки гипотез и излагать методику сравнения критериев, следует заметить, что ошибки при проверке гипотез неравнозначны. Ошибки принятия гипотезы 2, когда в действительности имело место распределение типа 1 (и наоборот) менее существенны, чем принятие гипотезы 3, когда было распределение типа 1 и уж тем более принятие гипотезы 1, в ситуации, когда имело место распределение 3. Это, вообще говоря, ясно из интуитивных соображений и подтверждается данными таблицы 3.

С учетом сказанного, целесообразно установить ограничение на число ошибок, заключающихся в принятии гипотезы 3, в то время как имело место распределение 1 и наоборот - гипотезы 1 при распределении 3. В частности, потребуем, чтобы относительное число таких ошибок составляло не более 1-2%. При выполнении этого условия будем сравнивать критерии по суммарному числу правильно принятых решений на векторах невязок, полученных моделированием трёх указанных выше распределений (1,2 и 3) одинаковое число раз.

Еще одно замечание. Для всех исследуемых далее эмпирических критериев, фигурирующий в них параметр масштаба s находится без решения уравнений. Для этого используются соотношения, полученные при проведении экспериментов по схеме п.3 для всех распределений:

№1: s о ; №2: s=0,546 -o и№3: s=0,48 -o . (13)

Теперь конкретизируем процедуру выбора вида распределения по эмпирическому значению величины нормированного кван тиля K q,j = F j1 (p0)о . Исходя из вида различаемых нами трёх распределений, лучше всего было бы взять р0 малым, чтобы квантиль был за пределами 2^2,5о, где различие трёх квантилей достаточно велико, однако при малой выборке это нереализуемо. Подсчёты по непрерывным плотностям показали, что можно взять р0= 1/3. Алгоритм работает следующим образом:

• 1)    Вычисляется выборочное с.к.о. о и среднее 2

• 2)    Значения выборки упорядочиваются по возрастанию и центрируются.

• 3)    Вычисляется значение квантиля F —Ч /З ) (оно отрицательно). В силу симметрии проверяемых распределений для повышения точности в качестве результирующего квантиля берётся

Q v,j ( ' ( ) ' F j - 1 ( 23 ))/ 2 .

Кроме того, так как при малом N округление от деления на 3 существенно, при вычислениях f ^{- 1} ( 13 ) и F ^{- 1} ( 23 ) делается коррекция в зависимости от остатка от деления N на 3.

• 4)    Величина Q _v (а сравнивается с теоретическими значениями для каждого из распределений. Они равны соответственно 0,43; 0,388; 0,277.

• 5)    Значение параметра s вычисляется по формуле (13) с учётом уже найденного вида распределения, вместо о подставляется о .

Проверка гипотез по критерию нормированного среднего модулей невязок

Рассмотрим особенности применения этого критерия для двух указанных выше способов нормировки. Вначале рассмотрим случай нормировки на среднеквадратичное отклонение. В этом способе величиной сравнения является S а /о . Приведём выражения для S а и о при трёх используемых распределений.

Распределение 1. - S _а = ^( 2 п ) s; o = s

Распределение 2. - S _а = 1,5 - s; с = 2s

Распределение 3.

В этом случае оба интеграла расходятся, поэтому ограничим интегрирование отрезком [-A;A].

Распределение 1.

S 1

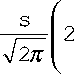
— exp > —

V

A ² i

2s 2 ,

Распределение 2.

~

³ а

s

Г A 2 ^

= -1п1+ — с

п

V

s

~ 2

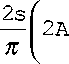
. A 1

s - arctg s 7

*

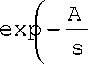
3          A2

- ( A + s ) +---

8          4s

В асимптотическом варианте, когда A

велико:

S 2

3s

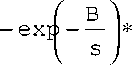
3           B2

- ( B + s ) +---

8         4s

A

s

2s

³ а =    ¹

п

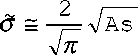
Распределение 3.

Нормированные величины будут следу

ющими:

23. Z A fs

V П ;4 ; \п S V A

s

S =

³ 2 п

( expi —

V

B2

2s2

7 f A2 1        _ lnH--— + 1111+---

B

V

^{V s 7}

V ^s

Равномерное распределение.

.

. (14)

. (15)

Опишем алгоритм:

• 1)    Вычисляется выборочное с.к.о. ст и среднее £ ".

• 2)    Значения выборки центрируются.

• 3)    Находится среднее значение

о

| £ = к - <  |

o

• 4)    Величина | ^ | /ст сравнивается с теоретическими значениями. При сравнении с распределением №3 берётся

oo

A = (max ^ - min ^ )/2 ; s = 0,48 - с т .

• 5)    Значение параметра s вычисляется по соотношениям (13).

Экспериментальные исследования показывают, что лучшие результаты, обычно, получаются при отличающихся от теоретических значениях нормированных величин: V2/ п + 0,0 3 6; 3/4 + 0,02; 0,675 . Для гипотезы 3 (распределение Коши) это значение существенно отличается от исходного теоретического, по-видимому, из-за того, что при малом объёме выборки N асимптотическое приближение неправомерно.

Теперь рассмотрим случай нормировки на площадь равномерного распределения . Вначале приведём выражения для площадей при различных распределениях. Отрезок интегрирования [-A;B].

s равн

A ² + B ²

2 (A + B ) .

Алгоритм реализуется в виде следующих шагов:

• 1)    Вычисляется выборочное с.к.о. ст и среднее ^ ^f

• 2)    Значения выборки центрируются.

  - o

• 3)    Находится среднее значение | £ | , oo

A =— min ^ ' , B = max £ . Площадь, соответствующая равномерному распределению, считается по формуле (17).

• 4)    Величина | £ /з _равн сравнивается с теоретическими значениями.

• 5)    Значение s вычисляется по формуле (13).

В отличие от нормировки на с.к.о. здесь нельзя заранее вычислить теоретические значения нормированных величин. Из выражений (14)-(17) видно, что пороговые значения зависят не только от выбранного параметрического класса распределений, но и от интервала [-A;B] ошибок. В свою очередь, этот интервал, для каждого заданного параметрического семейства, зависит от объема данных.

В качестве начального приближения для порогового значения брались значения, получаемые по формулам (14)-(17). А для вычисления границ интервала A и B использо-

Таблица 5. Проверка качества различения видов распределений

Тактическое распред еление Количество решений о гипотезе №: Сумма править-ных решений 1 2 3 Квадратичный критерий 1 54,3 43,4 2,3 155,33 2 28,3 66,3 5,4 3 0,4 26,1 73,5 Критерий нормированного квантиля 1 56,0 32,4 11,6 143,59 2 38,0 39,0 23,0 3 2,3 13,1 84,6 Критерий площади, отнесённой к с,к,о, 1 54,7 44,4 0,9 171,05 2 28,8 67,1 4,1 3 0,4 7,6 92,0 Критерий площади, отнесённой к площади при равномерном распределении 1 61,45 38,52 0,03 170,53 2 29,34 70,58 0,08 3 0,23 18,63 81,14 валась следующая эмпирическая формула

A=B=k(N)*s. (18)

Здесь k(N) - зависит от вида распределения и объёма выборки N так, что -A является квантилем 1/2N, а B -квантилем 1-(1/2N). Наилучшие результаты при N = 25 получились при нормированных величинах 0,896; 0,645; 0,355 соответственно для распределений 1, 2, 3.

Сравнение критериев

Проводилась сравнительная экспериментальная оценка критериев. В ходе эксперимента на каждой из 100 реализаций X, у осуществлялись следующие этапы:

• 1.    Моделирование реализации вектора ошибок для одного из заданных типов распределений (№1, 2 или 3). Параметры масштаба для них задавались на основе результатов исследований, приведенных в таблице 2. В частности, для распределения №1, s = 7 , для №2, s = 0,54 6 - 7 и для №3. s = 0,4 8 - 7 , где 7 - выборочное СКО.

• 2.    Решение задачи оценивания и вычис

• 3.    Определение (по невязкам) текущего значения критерия (одного из трёх) и выбор типа распределения в соответствии с заданным пороговым значением при моделировании трёх указанных выше распределений (1, 2 и 3) одинаковое число раз. Для сравнения критериев осуществлялась проверка качества различения видов распределений на тех же наборах данных. Для этого на исходные данные накладывался шум с распределением заданного класса (1,2 или 3) и подсчитывалось среднее по 100 экспериментам относительное число правильных и ошибочных решений для каждого распределения. Результаты приведены в таблице 5.

ление соответствующей реализации вектора невязок.

Заключение

Приведенные результаты экспериментов показывают, что параметрические семейства распределений компонент векторов ошибок и невязок в ситуациях, когда принимается гипотеза 3, соответствующая плотности распределения Коши, в большом числе случаев совпадают. По-видимому, это является следствием того, что для этого распределения характерным является больший вес числа выделяющихся ошибок, для которых такая связь проявляется более устойчиво.

С точки зрения надежности принимаемых решений наиболее эффективным является критерий нормированного среднего модулей невязок. Эффективность различения гипотез будет существенно больше, если вместо двух плохо различимых гипотез 1 и 2 использовать лишь одну (любую из них).

Использование описанных процедур проверки гипотез о параметрическом распределении позволяет повысить надежность и точность оценивания на каждой реализации. Их использование полезно на этапе адаптации алгоритмов, когда априорная информация о распределении ошибок в исходных данных отсутствует.

Работа выполнена при частичной поддержке Российского фонда фундаментальных исследований (РФФИ, грант № N 99-0100079).