Итеративный алгоритм линейного выравнивания, робастный по отношению к ошибкам оценок характеристик канала связи
Автор: Малютин А.А., Нечаев Ю.Б., Радько П.Н.
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 4 т.8, 2010 года.
Бесплатный доступ
Предлагается итеративный алгоритм совместной демодуляции-декодирования сигнала в многолучевых каналах с помощью линейного эквалайзера, особенностью которого является учет возможной неточности измерения изменяющихся во времени параметров канала связи.
Итеративные алгоритмы, многолучевой канал, последовательный модем, линейный эквалайзер
Короткий адрес: https://sciup.org/140191887
IDR: 140191887 | УДК: 621.396.4
Текст научной статьи Итеративный алгоритм линейного выравнивания, робастный по отношению к ошибкам оценок характеристик канала связи
Как показано в [1], ошибки оценок характеристик канала связи могут приводить к существенному снижению помехоустойчивости алгоритмов приема в многолучевых каналах, основанных на линейном выравнивании. Известны неитеративные алгоритмы, робастные по отношению к неточному измерению характеристик канала [2]. В связи с рядом существенных преимуществ итеративных процедур [3] целесообразно разработать их робастные аналоги.
Постановка и математическое описание задачи
Будем рассматривать задачу, сформулированную в [3], но с учетом возможной неточности оценок характеристик канала связи.
Целью использования SISO-эквалайзера является формирование мягких решений о передаваемом канальном символе – набора апостериорных вероятностей ^sk = к для каждого из z = 0, ... , M-\ его возможных значений ^ , где M = 2Q, a Q – количество двоичных бит в символе. На их основе формируются значения логарифмов отношения правдоподобия (LLR) для символов L {x„ = s, } (или бит L {cnQ+k = bitk (s,)}) кодового слова, передаваемых, после перемеже-ния, на вход символьного (или битового) SISO декодера. Критерием качества является средний квадрат ошибки оценки информационного символа.
Начиная со второй итерации для SISO-эквалайзера доступна поступающая по кольцу обратной связи (после соответствующего депе-ремежения) информация, которая может быть использована для улучшения характеристик эквалайзера на последующей итерации его работы.
Пусть длина регистра сдвига эквалайзера содержит N = TV, + N2 +1 ячеек, на каждом шаге (временном сдвиге на один символ) выносится решение о n -ом символе, занимающем Nv +1 положение в регис ре сдвига.
Пусть Уп [y»+w, ’•■•’ Уп’--ч Уи-уг] – вектор из TV, + N2 +1 элементов – символов, последовательно поступивших на вход приемного устройства, на основании которых выносится решение о символе X , наблюдаемых вместе с аддитивным шумом, описываемым вектором из TV, + TV2 +1 отсчетов шума w„ = k,+Mv..,w„,...,w„_^2] . Если временная протяженность импульсной характеристики канала h„=ко’-’кл-1] распространяется на L символов, то данному вектору принимаемых символов V соответствует вектор передаваемых символов Xn [-^n + V v-4Xn)--4Xn-N2+L-A ] из TV, + TV2 + L элементов.
Модель, описывающая искажения вектора передаваемого сигнала XR каналом с межсимвольной интерференцией и добавлением шума W(] , может быть представлена как
Уп = HnXn + W„ ’ (1)
где H n – канальная матрица размерности
(7V1+7V2+l)x(7V1+Af2+L).
При решении учитывается априорная информация обо всех передаваемых символах Xn ’ за исключением априорной информации о самом оцениваемом символе Xn ’ в соответствии с так называемыми турбо-принципами [4], согласно которым априорная информация об оцениваемом символе, поступающая на вход одной из ступеней итерационной обработки, не должна передаваться со входа на выход данной ступени.
Априорная информации доступна в форме логарифмов отношения правдоподобия для канальных символов, либо формируемых непосредственно самим SISO-декодером (при использовании символьного кодирования), либо рассчитываемых, исходя из битовых отношений правдоподобия, формируемых SISO-декодером (при использовании битового кодирования), начиная со второй итерации декодирования.
При перемежителе достаточно большой длины оценки можно считать независимыми, так как маловероятно, что после деперемежения в регистре сдвига эквалайзера длины окажутся символы, находившиеся на расстоянии менее нескольких длин кодового ограничения (когда возможна значимая корреляция решений) во входной последовательности декодера.
Будем искать оценку передаваемого информационного символа на выходе эквалай зера в виде линейной функции от вектора отсчетов принимаемого сигнала не накладывая ограничений на вид функции обратной связи . С учетом (1) можно записать х — атН х + агw — f. (2)
и п п п п п Т П' V /
Формально задача состоит в поиске оптимальных значений вектора весовых коэффициентов фильтра и сигнала, передаваемого по кольцу обратной связи , как функции от известных статистических характеристик шума, сигнала и оцененных параметров канала связи. Критерием оптимальности целесообразно выбрать минимизацию среднего квадрата ошибки оценки Усреднение должно проводиться:
-
- по ансамблю всех возможных значений вектора с учетом всей имеющейся априорной информации о передаваемых символах, за исключением априорной информации о самом оцениваемом символе ;
-
- по ансамблю всех возможных значений случайных величин элементов канальной матрицы при известных оценках этих элементов, образующих матрицу оценок
-
- по ансамблю всех возможных значений случайных величин отсчетов шума, при оцененных статистических характеристиках шума.
Обозначим данные операции вычисления средних значений как и соответственно. Тогда подлежащая минимизации величина среднего квадрата ошибки оценки будет иметь вид е" = Е . н \Е {|х — х I" ш = где – условная плотность вероятностей истинных значений при известных н„;рх\х„> – плотность вероятностей с учетом всей имеющийся априорной информации о всех передаваемых символах (включая оцениваемый ). Запись для плотности вероятностей не учитывающей информацию об оцениваемом символе предполагает независимость компонент вектора . Требуется най ти .
Подставляя (2) в (3) получим
8-11 Де - \11\\сЕ П х : \ и \\\ - х: - .1\ х
Я wn | wn к Н„ Н„ к Х\Хп к L п п пи п “п А х \атН х + атw —х — £ ш =
=Е Де Де .JUHxI"^
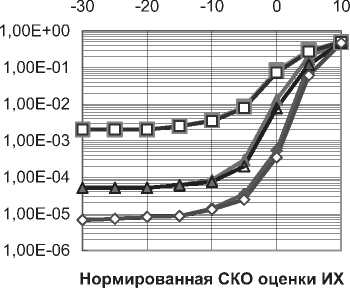
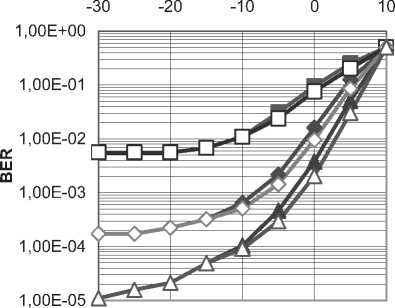
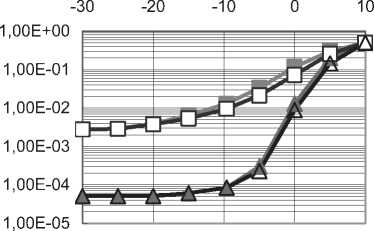
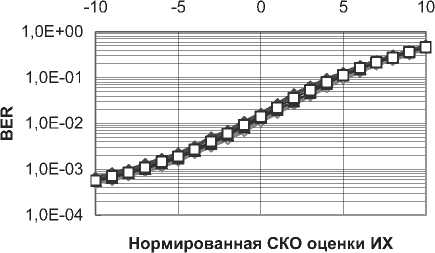
+атН х (c/w ) — агН х х* — И И мул и и п и И п YlTn п и Х Д'„ Н„Х„ ) +\ап W„ | * ап Wd,. * d WA * - х„ ^Нпхп)- хп (aTnwn) + |х„ |2 + xd* - Выполнив усреднение и приняв в расчет следующие соотношения: Е~ Ldw„ }= Е~ i(dw„) \=dEv {w„l = хп \ п п ) ХуДУ И и / ) и Xп к и ? Н J * 1 Т^ f 1 Т-1 / * 1 А а., ж f= Е~ f Е - у= О где усреднение проводилось с учетом априорной информации обо всех символах , за исключением оцениваемого , и было введено обозначение . Введем обозначения : вектор представляет собой вектор принимаемых символов, в котором значение оцениваемого n-го символа заменено нулевым, а вектор определяется как: е,. = [О,...,О;_„1,О,.+1,...,О]5 то есть является вектором длины из нулей с единицей на i-ой позиции; : вектор представляет собой просто n-ый столбец матрицы . Вычислим первые семь слагаемых, входящих в (4) с учетом введенных обозначений. С учетом (6) и (5) средний квадрат вероятности ошибки может быть записан как = Е ~ IE . ) \ат(Н х + х s ) I 4y„ гя„|я,д| ”Y » » » I ^X^N"^ X \НпХп + XnSn Y Y = L n n n n J ) J \ n ) = Er We i. {s„k|x„|2 + H^W + + H x xH HH + x s (H x У } = n n n n и n\ n nJ ) n) Подставив полученные выражения в (4), будем иметь 2 Tr J Я 1 * 2 . £„ = ah . \ахт + n n /у V n n ) n x \ T r? j ту [7 ~ II 1 rr // 1 * + ah ia Lxx \a — n ц m t n x„ \ n n ) n ) n - a s ty — a H x± + ^r ah i. ww, саи — аи sov + n WnVVn к И >1 ) И И n X xcE^^HS.V^- Вид функции обратной связи, минимизирующий может быть найден дифференцированием (5) по ^n . При вычислении учтем, что ^n – комплексное число и WJW„=^ согласно правилам дифференцирования по комплексному аргументу. В результате получим уравнение 0E,ja?„=-a^H„x„l+5>o, решая которое относительно , получим ^n ^n ^n^n * (6) £" = aTE . {55я Lz* + n n H v n n ) n х°;Ен,й\н,Е5.^„х^Н^ T ~ 2 ТЛ ~п\л II * . — asi1crv — aH \ххи аи + них n n \ n n J n n + a^E 1 a . n wn |w„ V. n n ) n Значения коэффициентов фильтра прямой связи an могут быть получены дифференцированием (7) по данному вектору д£7, / дап = О . Учитывая, что zT a = aT z , д^ат zY da = a и d[aTnz*Y dz = О (где а и z – комплексные векторы), будем иметь E„ ,й b" V>; + E,s. {нл. ^.x" V к - - ■ Uw к = 0. n x n \ n n J n n Wn I Wn к И n ) n Решая данное уравнение, получим ^^-^t^wj//^5"15» 4 + ^WhaWVeV ~E„!» {я„(44)ь!+ , 77 J я 1-1-1 „2 + E I W ( s (7 = ^ькьЬь +Ен.1й. b„K {xj;}- txEW}+ , 77 J я 1-1-1 + £,.I».K«'. j) s„ =ve„ 1Й Ь„"}4+яя |Я {я„^я;}+ + kv„|4HW»j] SWx, где d-ing\yn+Nx 5---1 Vn-1 ’ ^x ’ b+l ’•"’ Vn-Ni+L+\ ) представляет собой ковариационную матрицу вектора оценок информационных символов X, соответствующих принимаемому сообщению У» ’ вычисленную по ансамблю всех его реализаций с учетом априорной информации обо всех символах, за исключением символа .x^ , для которого Остальные величины рассчитываются как K~xJX'k =b) При использовании символьного кода расчет априорной вероятности символа в (9) производится, исходя из известных символьных отношений правдоподобия, сформированных декодером на предыдущей итерации обработки: РрЛх„ = sj = PprK = s0}exp№„ = s.}} = м-i = exp {£ ^x„ = s;}} / £ exp {£ {x„ = s;}}. 7=0 При использовании битового кода расчет производится, исходя из набора отношений правдоподобия, формирующих данный символ бит l + ^(5z)exp{z{c g+,}} ^+ёхр{Е^~}р = bitk(s^ = где ЬИк($;) – значение к -го бита, информационного символа, которому соответствует сигнальная точка созвездия Sj , имеющая метку i. Расчет априорных вероятностей бит, формирующих символ на входе декодера, исходя из отношений правдоподобий данных бит l + exp{z{c„e+;}} ,^{0,1}. Диагональная структура матрицы Ун ’ как упо- миналось выше, следует из независимости величин xi при использовании перемежителя большой длины по сравнению с длиной кодового ограничения используемого кода. Удобно выразить Vn через ковариационную матрицу всех (включая и xn ) априорных средних значений входных символов : К =E- {x хя}-(х Xя) = n xn v n n ) \ n n ’ = diag^Nx ,...Уп_хУ„^,.^ для чего можно представить последнюю матрицу в виде Рц Ki + VneN, +ieN, +1 ' Подставляя последнее выражение в (8), получим EH^ZH^-v^ + ^.W^E^ которое далее можно преобразовать, используя лемму об обращении расширенной матрицы [7]: (A + abHyl = A~l- А~'аЬнА~' 1 + bH A~'a Окончательно будем иметь: an ^x Ец щ \HnVnHn } + £" |^ {и’пи’;; } 5,; / l + (l-v^/^)x (10) Y^Hn\Hn ^H»EHn } + EWn\^,n{wnwn }J s„. Таким образом, коэффициенты эквалайзера представляют просто масштабированный вектор к„|я„ ^НУпН” 1 + EK>n {w„w^ }]-' S„, поскольку сомножитель в виде дроби является обыкновенным скалярным числом. Выражения (6) и (10) полностью описывают операции, выполняемые SISO-эквалайзером для получения оценки символа xn . Далее полученная оценка используется для расчета набора апостериорных вероятностей Pp.skXn ^/} ^ 0, ... , M 1, по которым определяется набор внешних отношений правдоподо-бияCK="J или набор внешних отношений правдоподобия для всех образующих символ бит£ХКр+А' = bitk<Si^, в зависимости от вида используемого кода (символьного или битового). После деперемежения peqv {•••}- LcodV-Д поступают на вход SISO-декодера. Как и в случае точно известных характеристик канала связи [5], коэффициенты фильтра изменяются во времени, то есть должны пересчитываться для каждого оцениваемого символа, причем даже для стационарного канала связи с канальной матрицей Hn , не зависящей от временного индекса n. Рассмотрим случай отсутствия априорной информации, соответствующий первой итерации оценки, то есть случай, когда X; = 0 для всех i и E = ^x1 • Тогда коэффициенты трансверсального фильтра и сигнал в цепи обратной связи будут рассчитываться как Если при этом характеристики канала и шума известны точно, то есть определено E {H Нн}^ H HH ,E Ы wH\ = w wH, u n \ И n , to a* = cr; x \a"vHH” + w„w” и, /7 /7 ’ /7 X L -V П П П П J ’ таким образом, предлагаемый вариант эквалайзера превращается в классический линейный эквалайзер без обратной связи [8]. В противоположной ситуации, когда точно известны все символы, кроме оцениваемого, соответствующей последним итерациям при большой величине отношения «сигнал /шум», имеем: v„2 -0, xn = xn, xn=xn и Y^^e^e"^. Подставив в (6) и (8), получим = Й:а ^EH^S^ Выражение (11) представляет собой просто масштабированный вариант согласованного (с ожидаемым сигналом, искаженным каналом) фильтра, а (12) – сигнал МСИ от других элементов сообщения, в предположении, что элементы сообщения известны точно. Расчет условной плотности вероятности распределения компонент вектора ИХ канала и корреляционной функции отсчетных значений шума при известных величинах их оценок Для вычисления E^.W,входящих в (8) -(12), необходимо располагать условной плотностью вероятностей распределения компонент вектора ИХ при известных величинах их оценок. Для каждой модели канала известна априорная плотность распределения вероятностей p pr(h) . Для каждого способа оценки ИХ канала h можно считать известной P(h | A) . Тогда совместная плотность вероятности pUiJY может быть найдена как pViJi> = pVA^ PprW, а затем и искомая условная плотность вероятностей может быть получена как p(h | A) = p(h | A) ppr(Ji)l \p(h | h)ppr(h)dh. Если считать, что ошибка оценки имеет гауссовское распределение, то справедливо mh R R AA AA RhhRW’ , где mh = E^ , a Rhh=Eh^h-mhXh-mhh)HY R- - = E- {(A - m- )(A -тЛн\ AA Av A z x h7 ) R ■ = E ■ {(A - mh )(A - m ■ )"}, Rn = E. {(A - m -)(A - mh )H}, и тогда искомая плотность вероятностей будет также гауссовской: P(A|A)|^| exp {-(a ^^Eh^Vm^R^h-Tn?) и Rh\h = Е1АЙ {(A - «J(A - mA| -) ^ Rhh - R^R^. ^=№'+^)"1- Согласно используемой модели канала можно считать, что mh = 0 и следовательно, при несмещенной процедуре оценки Vmh = mh = °) , получим mh\h= ^ . При достаточно высокой точности оценки ИХ можно считать, что 1Ы»1К/,д/,||, где ll-ll – матричная норма, тогда ^A|A ^ ^ААДА . Считая ошибку аддитивной, то есть rr,f"^n "1” Av/Z , можно записать Ew„\wn ^Rwn ^ RW„ + Raw,,- гдеR Оценка вычислительной сложности алгоритма и методы ее уменьшения Основной сложностью при реализации предлагаемого алгоритма, работающего в реальном масштабе времени, является задача расчета коэффициентов фильтра прямой связи ^n , требующая обращения матрицы An=EH |й $tHynH^ + Ew>3wnw»Y Данную операцию необходимо выполнять для каждого информационного символа и на каждой итерации оценивания. Операция непосредственного обращения матрицы NxN требует N арифметических операций. Размерность N данной матрицы, определяемая памятью канала, бодовой скоростью и требуемой помехоустой- чивостью (длиной фильтра), может доходить до 25…35. Даже для относительно невысоких скоростей передачи информации, характерных для КВ-канала, вычислительных ресурсов для выполнения этой операции в реальном времени путем непосредственного вычисления обратной матрицы будет явно недостаточно ни при каком программном или даже чисто аппаратном способе реализации – как в настоящее время, так и в обозримой перспективе. Поэтому необходимо найти эффективные в вычислительном отношении способы выполнения данной операции. Предлагается рассмотреть варианты как точного решения этой задачи, учитывающие специальную структуру матрицы в зависимости от характеристик канала, так и приближенного ее решения. Варианты точного вычисления обращаемой матрицы, применимые только для случая стационарного канала (нп=н является теплицевой эрмитовой матрицей): - рекурсивная процедура вычисления обратной матрицы Ап на основе знания обратной матрицы Д4 , использующая метод, основанный на специфических свойствах канала связи [1]; - алгоритм Левинсона-Дербина; - алгоритм Шуры; - алгоритм факторизации Холецкого. Все вышеупомянутые методы обладают вычислительной сложностью реализации (N + Lf . Для каналов с достаточно протяженной ИХ (Т>15) реализация их на современной и планируемой на ближайшую перспективу аппаратной платформе является проблематичной. Предложим следующие упрощенные варианты предлагаемого робастного алгоритма. Первый упрощенный вариант робастного алгоритма Суть предложения состоит в аппроксимации диагональной матрицы V единичной (с масштабным коэффициентом), усреднении ее диагональных элементов Vn (априорных дисперсий оценок информационных символов) за некоторый интервал времени. Это позволяет производить расчет обратной матрицы Ап не на каждом символьном интервале, а один раз для всего интервала усреднения. Усреднение величины априорных дисперсий оценок информационных символов (элементы матрицы V,) производится на интервале некоторой длины K методом скользящего окна: п + К/2 Ч-к" (13) j=n-K/2 Тогда Уп « v 4 и 4 - 4 = ^Ен й {НпН^} + Ew>-1 {WnWHn}. В таком случае обращение Аи можно проводить не на каждом шаге работы эквалайзера, а один раз на интервале внутри интервала усреднения. Вычисление Ап для (12) может проводиться точно, поскольку выполняемые над ним операции не требуют больших вычислительных затрат (по сравнению с задачей обращения). Тогда коэффициенты эквалайзера будут вычисляться как «;= Ki».(//.w") + £-.i*.(“'."'"!?^! где V определяется (13). А коэффициенты фильтра обратной связи будут по-прежнему рассчитываться при помощи (6), но с использованием (14) вместо (10). Минимальная длина интервала усреднения здесь равна длине фильтра TV, + N2 +1, а максимальная ограничивается интервалом стационарности характеристик канала. В случае стационарного канала усреднение диагональных элементов vn может быть проведено на всем интервале кодового слова, тогда в результате предельного перехода при неограниченном повышении точности оценок ИХ данный вариант превратится в предлагаемый в [5]. Второй упрощенный вариант робастного алгоритма Вариант, состоящий в точном вычислении обратной матрицы AH для определенных символов, выбираемых с некоторым интервалом, и определении коэффициентов фильтров внутри данного интервала с использованием какого-либо алгоритма адаптивной фильтрации или адаптивного сглаживания. Точность, очевидно, будет тем выше, чем чаще будут выбираться узловые точки, в которых коэффициенты фильтра будут вычисляться точно. В качестве методов адаптивной подстройки коэффициентов эквалайзера могут использоваться адаптивные алгоритмы: наименьших квадратов (LS); рекурсивных наименьших квадратов (RLS); калмановской фильтрации. —■—Eb/No=7 dB —*—Eb/No=8dB —•— Eb/No=10 dB —D—точн. роб. алгоритм, Eb/No=7 dB А точи. роб. алгоритм, Eb/No=8 dB —О—точн. роб. алгоритм, Eb/No=10 dB а) Нормированная CKO оценки ИХ —■—Eb/No=14 дБ —♦—ЕЬ/Ыо=18дБ -*-Eb/No=22 дБ —□—точн. роб. алгоритм, Eb/No=14 dB — О—точн. роб. алгоритм, Eb/No=18 dB — А— точн. роб. алгоритм, Eb/No=22 dB б) Рис. 1. Влияние точности оценок компонент вектора отсчетов дискретной ИХ на помехоустойчивость оптимального робастного алгоритма итеративного приема и алгоритма, построенного в предположении точных оценок ИХ а) 8PSK; б) 64QAM Первый алгоритм является наиболее простым, а два последних, по сути, очень близки, и при определенных условиях [9] RLS может рассматриваться как частный случай калмановской фильтрации, обеспечивая более быструю сходимость (по сравнению с LS). Для повышения точности целесообразно использовать алгоритмы не адаптивной фильтра- ции, а адаптивного сглаживания [9], отличающиеся тем, что критерием подстройки коэффициентов фильтра является минимизация сигнала ошибки не в одной точке, а в нескольких [9]. Результаты моделирования Характеристики помехоустойчивости предлагаемых вариантов, полученные при помощи моделирования, изображены на рис. 1 для случаев: а) 8PSK; б) 64QAM. Кодированная модуляция BICM-ID во всех случаях, количество итераций декодирования проводилось до достижения полного насыщения. Использовалась модель многолучевого канала 1б [10]. О' ш со Нормированная СКО оценки ИХ ■ стандартный алгоритм, канал 1а А стандартный алгоритм, канал 16 —□—робастный алгоритм, канал 1а А робастный алгоритм, канал 16 Рис. 2. Влияние вида ИХ на помехоустойчивость робастного алгоритма, 8PSK, BICM-ID • стандартный алгоритм —О—точный робастный алгоритм ▲ 1-й упрощённый алгоритм — D— 2-й упрощённый алгоритм Рис. 3. Характеристики помехоустойчивости упрощенных робастных алгоритмов На рис. 2 изображены кривые помехоустойчивости для каналов 1а и 1б [10]. Видно, что в худшем канале выигрыш робастного алгоритма больше. На рис. 3 приведены характеристики помехоустой- чивости упрощенных робастных алгоритмов для сигнального созвездия 8PSK в канале 1б при кодированной модуляции BPSK-ID. В первом упрощенном алгоритме использовалось усреднение на длине эквалайзера для каждого оцениваемого символа. Во втором упрощенном алгоритме использовался адаптивный RLS фильтр для подстройки коэффициентов эквалайзера между узловыми точками, расположенными на расстоянии, равном длине фильтра. Выводы 1. Величина энергетического выигрыша от использования предлагаемого алгоритма по сравнению с построенным в предположении точно известной ИХ в области ошибок оценки, представляющих практический интерес, лежит в пределах 0,2 - 0,7 дБ. 2. При увеличении кратности используемой модуляции и «ухудшении» вида ИХ преимущество робастного алгоритма возрастает. 3. Робастность по отношению к ошибкам измерения дисперсии шума не дает значимого выигрыша помехоустойчивости в области представляющих интерес значений ошибок. 4. Строго оптимальный вариант робастного алгоритма обладает неприемлемой вычислительной сложностью реализации даже при использовании специальных методов быстрого обращения матриц. 5. Два предложенных приближенных метода значительно уменьшают объем необходимых вычислений при приемлемом снижении величины энергетического выигрыша. Ни один из методов не имеет явных преимуществ перед другими и при определенных условиях наилучшим может быть любой из них. Работа выполнена при финансовой поддержке РФФИ (проекты 08-02-1355-офиц, 09-07-97522-р-центра).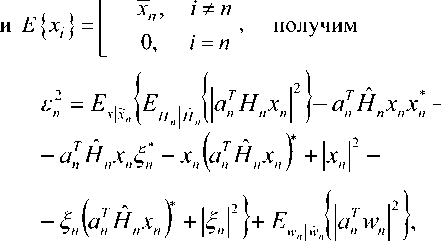
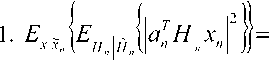
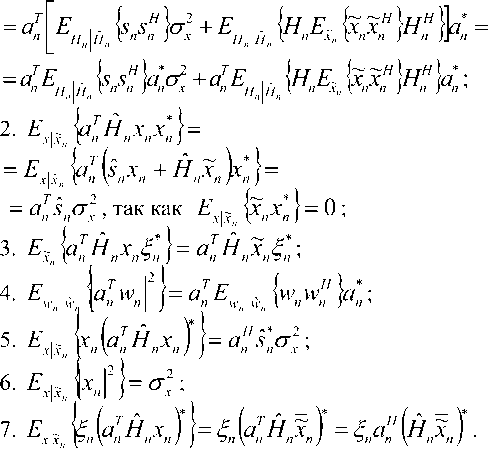
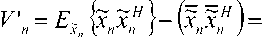
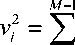
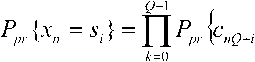
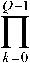
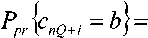
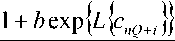
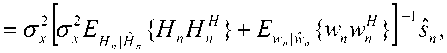
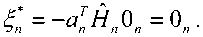
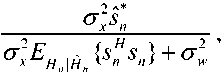
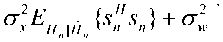
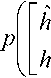
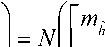
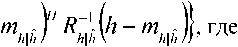
Список литературы Итеративный алгоритм линейного выравнивания, робастный по отношению к ошибкам оценок характеристик канала связи
- Нечаев Ю.Б., Малютин А.А. Методы оценки параметров многолучевого канала связи при итеративных алгоритмах приема//Теория и техника средств связи. №2, 2009. -С. 13-25.
- Liavas А. On the robustness of the finite-length MMSE-DFE with respect to channel and second-order statistics estimation errors//IEEE Trans. Signal Processing. Vol. 50, Nov, 2002. -P. 2866-2874.
- Otnes R., Tüchler M. Block SISO linear equalizers for turbo equalization in serial-tone HF modems. 2004. http://citeseerx.ist.psu.edu>
- Otnes R., Tüchler, M. On iterative equalization, estimation, and decoding. 2008. citeseerx.ist.psu.edu' TARGET='_new'>http://>citeseerx.ist.psu.edu
- Tuchler M., Koetter R., Singer A. Turbo equalization: principles and new results//IEEE Transactions on Communications. Vol. 50, No.5, May 2002. -P. 754-767.
- Lee S.-J., Singer A., Shanbhag N. Linear turbo equalization analysis via BER transfer and EXIT charts//IEEE Transactions on Signal Proc-essing. Vol. 53, No.8, Aug. 2005. -P. 2883-2897.
- Уоткинс Д. Основы матричных вычислений. М.: Бином, 2006. -664 с.
- Прокис Дж. Цифровая связь. М.: Радио и связь, 2000. -800 с.
- Haykin S. Adaptive Filter Theory. Third edition. -990 с.
- Нечаев Ю.Б., Малютин А.А., Радько П.Н. Помехоустойчивость итеративных алгоритмов приема в многолучевых каналах с неточно известными параметрами//Теория и техника радиосвязи. №4, 2009. -С. 23-28.


