Итеративный алгоритм расчета скорости и затухания трубных волн по данным акустического каротажа

Оценка скорости и затухания волны является базовой задачей при обработке данных акустического каротажа [1]. По этим параметрам акустической волны определяют физические и механические свойства околосква-жинной породы (например, [2]).

Распространенным методом обработки данных акустического каротажа являются метод Прони [3] и его модификации [4, 5]. Недостатками метода Прони являются большое количество выбросов в значениях оцениваемых параметров и большая погрешность в оценке коэффициента затухаемости. Чтобы преодолеть эти недостатки был разработан гомоморфный метод [1], который будет подробно рассмотрен далее. Однако при малом количестве приемников и высокой зашумленности данных, как будет показано ниже, гомоморфный метод приводит к большой погрешности в оценке затухаемости волны. В качестве шумов могут присутствовать как измерительная погрешность аппаратуры, так и искажения вследствие наложения различных типов волн.

Для обработки данных с высокой зашумленностью был разработан метод предсказания [6, 7]. Этот метод устойчив к шумам данных, но позволяет оценивать только скорость волны. Кроме того, он не позволяет проводить дисперсионный анализ и, таким образом, может с достаточной надежностью применяться в анализе только продольных и поперечных волн, исключая дисперсные волны Стоунли.

Общей особенностью всех этих методов является то, что в них изначально выбирается или временная или частотная плоскость для последующих расчетов. Так в методе Прони и его модификациях расчеты выполняются в частотной плоскости. Это приводит к тому, что результаты оценок параметров базовым методом Прони по зашумленным данным имеют большие выбросы. Сглаживание получаемых оценок в гомоморфном методе [1] делает их более устойчивыми к шумам. Однако точность оценок в некоторых полосах частот снижается. Кроме того, гомоморфный метод применим только в том случае, если отсутствуют искажения вследствие наложения различных типов волн.

В методе предсказания [6] расчеты выполняются только во временной плоскости. Это исключает возможность проведения дисперсионного анализа.

Предлагаемый в данной работе метод использует в расчетах и временную и частотную плоскости. Поэтому он сочетает достоинства упомянутых выше методов. Он устойчив к шумам, позволяет работать с малым количеством приемников и выполнять дисперсионный анализ.

Идея использования и временной и частотной плоскостей в итеративном подходе к оценке требуемых параметров не нова. Она применялась в оптике, астрономии [8,9], при расчете дифракционных оптических элементов [10, 11].

Результаты работы предложенного итеративного алгоритма сравниваются с гомо- морфным методом. Приведем описание гомоморфного метода.

Гомоморфный метод определения скорости и затухания трубной волны

В общем случае для нахождения требуемых параметров волны необходимо решить волновое уравнение [12]:

1 ^{s ( z} ’t) =

(2p)

¥

¥

J d w exp( - i w t ) J dkX(k , w ) exp( - ikz)

-¥

-¥

где s(z, t) - отклик, записанный на приемни ке, z - расстояние между излучателем и приемником, t - время, w - частота, k - волно вое число. Выражение X(k,w) включает в себя информацию о геометрии модели, излучателе, граничных условиях и т.д. Для реализации и гомоморфного и итеративного алгоритмов не требуется знать точный вид вы ражения X (k ,w).

Записывая (1) в частотной плоскости и выполняя интегрирование по контуру в плос кости комплексного волнового числа, полу чим выражение, состоящее из суммы выче тов, охваченных контуром, и двух ветвящих ся интегралов

J, cut

[13]:

1 ^¥

S (z, w ) = —   dkX (k , w ) exp( - ikz) =

2 p

-¥

= i V R j exp( - ikz ) + [                (^

'                       Ccut

В некоторых частотных диапазонах основной вклад в (2) вносит лишь один вычет. Экспериментально установлено [1], что так происходит для трубной волны в диапазоне от 0 до 5 kHz.

Пусть спектр волны на первом приемнике имеет вид:

s1( w) = A(w)exp(ij>(w)).(3)

Спектр волны на втором приемнике описывается в виде:

s2 (w) = s( w) exp(ik (w )l),(4)

где l - расстояние между приемниками, k ( w )

- комплексное волновое число.

Запишем k ( w ) в виде:

k (w) = kr (w) + ia (w),(5)

где k r (w ) - описывает скорость волны, a ( w ) - затухание волны. Тогда (4) можно переписать в виде:

s ₂ (w) = A( w) exp( - a (w )l) x x exp(i( j(w) + k_r (w)/))

Необходимо оценить параметры k r (w ) и a(w ) по измеренным сигналам на приемниках во временной плоскости.

Вычислим натуральный логарифм s₂(w ) и выделим действительную и мнимую части:

^ [ ln s₂(w ) ] = ln A(w ) - a (w )l , (7)

□ [ ln s ₂(w) ] =

= Развернутое значение [ j(w) - k_r (w)/ ] . (8)

Выражения (7) и (8) описывают прямые линии. Выражение "развернутое значение" в (8) подразумевает [1], что полученные по модулю 2п значения "разворачиваются" в прямую линию добавлением чисел 2 пп, где n - целое, т.е. выполняется операция, обратная взятию по модулю 2 п . Коэффициенты этих прямых можно найти, используя метод наименьших квадратов (МНК). В этом и заключается определение скорости и затухания акустической волны гомоморфным методом.

Итеративный алгоритм определения скорости и затухания трубной волны

Применение гомоморфного метода дало хорошие результаты при использовании большого количества приемников (12) и малом затухании волны [1]. Чтобы более точно оценивать требуемые параметры, предлагаем интерпретировать вычисления, выполняемые в гомоморфном методе, как "половину итерации". То есть, имея отклик на нескольких приемниках во временной плоскости, переходим в частотную плоскость, выполняя преобразование Фурье. Далее, в соответствии с гомоморфным методом, находим коэффици- енты прямых - kr (w) и a (w), но не заканчиваем на этом расчеты, а переходим опять во временную плоскость. Здесь, получившуюся фазу мы оставляем неизменной, а результирующую амплитуду заменяем на амплитуду отклика на приемниках. На этом единичная итерация заканчивается.

Кроме того, в процессе итераций мы полагаем, что k_r ( w ) и a ( w ) являются линейными функциями частоты. Такая "линеаризация" увеличивает быстродействие алгоритма и делает его более устойчивым к шумам. Для выполнения более точного дисперсионного анализа значения k r (w ) и a ( w ) можно аппроксимировать полиномами степени большей, чем первая.

Формально предлагаемый алгоритм для двух приемников записывается в виде:

Пусть 1 s(t ) и ₂ s(t ) - отклики на первом и втором приемниках, соответственно. 1 S⁽ щ ) = ^ф{ s⁽t^)}=A^exptiG Ф^))^-] ^{- ф}урье-спектр отклика на первом приемнике.

• 1.    Полагаем отклик на втором приемнике начальным приближением ₂ s(t )=₂s₀ (t) .

• 2.    Находим Фурье-спектр

• 3.    Находим значения a_n и c n из условия

2 ^Sn ⁽ Ю ) = ^ф{ 2 s n ^{( t )}}= 2 A n ⁽ Ю ) ^exp[i⁽ 2 Ф n ⁽ Ю ^))] , где n - номер итерации.

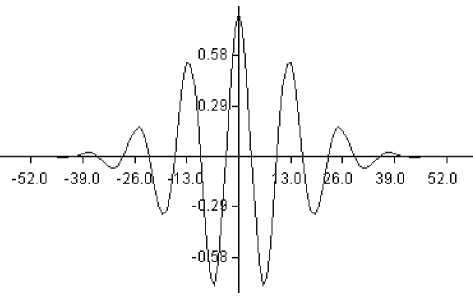
Рис. 1. Сигнал на нервом приемнике

Численные результаты

В качестве тестового сигнала на первом приемнике использовался (рис.1)

(

. 20р,. N i s(ti) = cos( — (i - у)) exp

^^^^^^^в

•i- N'2]

А2

. (11)

\            7

min iZ

a n ^{, c}n

w

In

2 A n ( w ) 1 A( w )

+ a^w - c   У n n ,

находим значения k_n из условия

min 1 Z ^[i j^(w ) ^{+ k} n ^w-2 j n ^{(w)] 2} * .

где N = 128 - количество отсчетов сигнала, А = 20, i = 1 k 128 .

Умножив Фурье-спектр сигнала (11) на коэффициент, описывающий затухание, и выполнив обратное Фурье-преобразование, получим сигнал на втором приемнике (без запаздывания)

2 S ^{( t}i ) = ^ф-1 { ^exP⁽ « ^{i )Ф[} 1 S ^{( t}i )] } , ⁽¹²⁾

На рис.2 показаны амплитуды сигнала на первом приемнике и, получившегося в результате операции (12), сигнала на втором приемнике.

На рис.3 показана фаза сигнала на втором приемнике. Заметно, что операция (12) приводит к небинарной фазе. Подобное искажение фазы может происходить, например,

kn

w

4. Выполняем обратное Фурье-преобразование

2 s n + 1

(t ) = Ф — ¹

1 A( w ) exp( - a _n w + c_n ) x

1                                      r lx eXP(1 j(w) + knw)    J

5. Выполняем замену

₂ s^p n + i (t ) =

^{2 s ( t} )

| 2 S n + 1 (tГ n ^+1()] .

Переходим к шагу 2 или заканчиваем итерации, если изменение ₂ s n (t ) меньше за

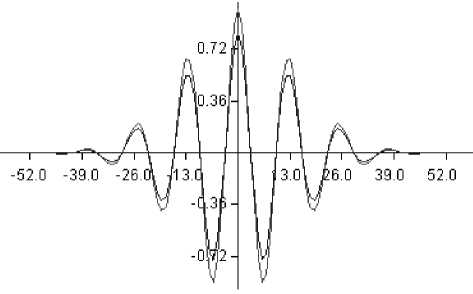
Рис. 2. Сигнал на первом приемнике и сигнал на втором приемнике с коэффициентом затухания

данной погрешности.

a = 0.003

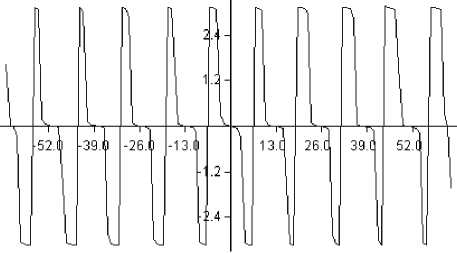
Рис. 3. Фаза сигнала на втором приемнике

при наложении друг на друга поперечной волны и волны Стоунли. Выражения (7) и (8) для модели (6) не учитывают возможности такого искажения фазы. Таким образом, цель предлагаемого итеративного процесса - точное восстановление сигнала (в том числе -фазы на втором приемнике, рис.3, включая оценку значений запаздывания и затухания сигнала, рис.4).

На рис.4 показаны амплитуды сигнала на первом приемнике и, получившегося в результате операции (12) и сдвига по времени для k = 0.1, сигнала на втором приемнике.

Эффективность работы предложенного итеративного алгоритма проверялась на зашумленных сигналах, показанных на рис.5. На этом рисунке представлены сигналы на первом и втором приемниках с коэффициентом затухания a = 0.003 и запаздыванием k=0.1, искаженные гауссовым шумом с дисперсией d = 0.01.

В результате численных экспериментов было установлено, что предложенный алгоритм обладает различными скоростями сходимости для двух оцениваемых параметров. Алгоритм сходился к правильному значению запаздывания за две итерации, в то время как для точной оценки затухания требовалось 1015 итераций. Такое различие можно объяснить различным характером воздействия шума на амплитуду и фазу сигнала.

Действительно, зашумленный сигнал на приемнике можно записать в виде:

s(w) = (A( w)exp(-a(w)l) + ea) x x exp(i(j (w) + kr (w )l + ef ))      , где ea и ef - шумовые компоненты амплитуды и фазы, соответственно. После логарифмирования вариация фазы записывается в виде:

A ( 3 [ ln s(w ) ] ) = A ( e _f ) .

Таким образом, преобразование не меняет вариацию фазы, и, следовательно, оценку скорости.

Используя разложение в ряд, вариация амплитуды записывается в виде:

^A(^^[lns⁽ w ^)])=^A( e a )

exp( a ( w ) l ) A ( w )

Т.е. вариация амплитуды растет экспоненциально с ростом расстояния l между приемниками, что затрудняет оценку величины затухания.

Для генерации гауссова шума из равномерной случайной выборки использовался алгоритм Бокса-Мюллера. Генерация равномерной случайной выборки выполнялась с помощью алгоритма Ранеку [14].

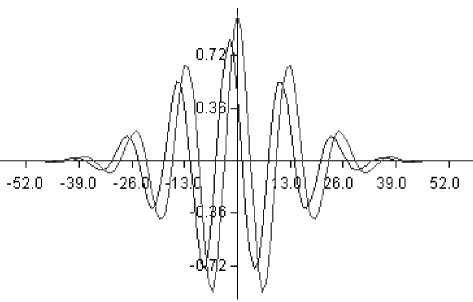
Рис. 4. Сигнал на первом приемнике и сигнал на втором приемнике с коэффициентом затухания a = 0.003 и запаздыванием k = 0.1

Для примера, представленного на рис.5, при оценке величины запаздывания алгоритм сошелся к правильному значению за две итерации, причем после первой итерации (что соответствует оценке гомоморфным методом)

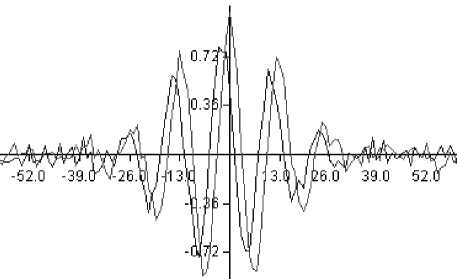
Рис. 5. Сигнал на первом приемнике и сигнал на втором приемнике с коэффициентом затухания a = 0.003 и запаздыванием k = 0.1 , искаженные гауссовым шумом с дисперсией d = 0.01

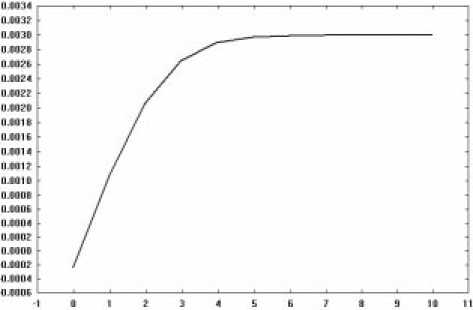
Рис.6. Зависимость оценки коэффициента затухаемости от числа итераций ошибка составляла всего 2%. Для оценки коэффициента затухаемости потребовалось 10 итераций, чтобы получить ошибку менее 1% (рис.6).

Выводы

Численные эксперименты показали работоспособность предлагаемого метода. Особенно эффективен новый метод по сравнению с гомоморфным методом при оценке затухания зашумленной акустической волны. Предполагаются дальнейшие исследования, направленные на разделение различных типов волн, присутствующих в сигнале, и оценку их параметров.