Из опыта преподавания. I. Симметрия - диссимметрия - антисимметрия

В 1993—1999 гг. в «Записках ВМО» были опубликованы 16 статей Д. П. Григорьева под названием «Из опыта преподавания минералогии», 15 из них изданы Н. П. Юшкиным отдельной книгой [2] в издательстве «Геопринт». Значение этого цикла, написанного одним из создателей современной минералогии, трудно переоценить, поскольку в нём обсуждаются наработанные десятилетиями методические приёмы преподавания. Авторы статьи призывают коллег продолжить цикл Д. П. Григорьева под более общим названием — «Из опыта преподавания», имея в виду все дисциплины, уместные на страницах «Вестника института геологии Коми НЦ УрО РАН».

«Одним из существенных условий прогресса знаний является объединение и совместное изучение всех тех явлений, которые явно имеют в себе общую сторону. Изучая их именно с этой стороны, мы, несмотря на несхожесть их в других отношениях, сливаем их в один объект знания <...>. Только прогрессируя в таком объединении знания, мы при нашем ограниченном уме, продолжительности жизни и других несовершенствах нашей природы, можем в единичном интеллекте совместить знания, которые при индивидуальном исследовании явлений представлялись бы неизмеримыми, необъятными и даже прямо безграничными. <^> Мы явно шли бы навстречу полному разъединению и непониманию друг друга, если бы познание основных начал сходства знаний самого разнообразного рода <^> не облегчало бы схватывания интеллектом всё большего умственного материала в связи с более совершенной организацией этого материала» [6, с. 3].

В указанном аспекте далее обсуждаются концепции симметрии, диссимметрии и антисимметрии. Связь первых двух достаточна наглядна, чего нельзя сказать о третьей. Диссимметрия (по П. Кюри) — исчезновение некоторых элементов симметрии [3, 7, 10]. Но антисимметрия определяется как симметрия плюс «перекрашивание», то есть радикальное изменение физического свойства тела [9, 11]. Физическое свойство возникает здесь неожиданно. Авторы предлагают иной логический приём, не выводящий за рамки геометрической кристаллографии, «сливающий в один объект знания» все три концепции и допускающий развитие теории.

Ровно 350 лет назад Н. Стеной впервые сформулировал закон постоянства углов между соответственными гранями кристаллов — один из краеугольных камней кристаллографии [5, 12]. Но подоплёка этого закона — видимое искажение формы кристалла при движении граней вдоль нормалей, о чём и идёт речь в статье. В следующем году исполнится 90 лет с выхода в свет основополагающей статьи Г. Хееша об антисимметрии. Авторы определяют её, используя всё то же движение граней вдоль нормалей. Так связываются две концепции, отстоящие в истории кристаллографии на 260 лет. Это побудило авторов посвятить статью обеим датам.

Симметрия — диссимметрия

Концепция диссимметрии вводится в университетском учебнике [4, с. 135—138] как понижение симметрии кристалла (выпадение некоторых её элементов), если его точечная группа симметрии (т.г.с.) не вкладывается, с учётом ориентировок элементов симметрии, в предельную группу симметрии среды. Здесь следует подчеркнуть, что искажение идеальной формы! кристалла определено различным развитием граней простой формы, а последнее — различной скоростью их роста. Высшее достижение в анализе искажённых простых форм — полное перечисление ложных простых форм 1-го рода (подформ) в каждом из 32 классов симметрии [8]. Принцип перечисления — систематическая декомпозиция каждой идеальной простой формы в совокупность таковых с меньшим числом граней.

Авторы подошли к решению той же проблемы иначе. В статьях [13, 14] дано определение реальной кристаллографической простой формы (р.к.п.ф.) как выпуклого полиэдра, ограниченного некоторыми гранями исходной простой формы, находящимися в правильной ориентации, но на любом расстоянии от начала координат. Компьютерное перечисление р.к.п.ф. для любых простых форм и их комбинаций дало инструмент для описания полного разнообразия диссимметричных кристаллов [1]. Так, октаэдр порождает 33 комбинаторно различных р.к.п.ф., ромбододекаэдр — 625, комбинация куба и октаэдра — 77657. В целом число р.к.п.ф. растёт с числом непараллельных граней и различных межгранных углов в исходной простой форме. Это огромное, но исчислимое разнообразие форм — тот ресурс, из которого природа выбирает реализации, сообразуясь с физической целесообразностью. В указанных случаях все р.к.п.ф. по необходимости_отно-сятся к подгруппам предельно высокой т.г.с. т 3 т . В общем случае вопрос о соотношениях т.г.с. исходной простой формы (их комбинации) и её р.к.п.ф. не изучен.

Диссимметрия — антисимметрия

Концепция антисимметрии вводится в учебнике [4, с. 187—188] как композиция симметрии и «перекрашивания» (например, отображение одного индивида на другой при описании двойников, переход от «положительного» кристалла к «отрицательному» и т. д.). Покажем, как она вытекает из концепции диссимметрии.

При генерировании р.к.п.ф. движение граней вдоль нормалей допускалось лишь вовне, что моделировало анизотропный рост кристалла. Но что будет, если переместить все грани вдоль нормалей на другую сторону от начала координат (назовём это радикальной диссимметризацией), для определённости — на то же расстояние? Если исходный полиэдр не содержит элементов симметрии 2-го рода, то полученный полиэдр энантиоморфен исходному. А с учётом изменения ориентировок нормалей к граням на противоположные он даже антисимметричен исходному (эвертирован, от англ. to evert — «выворачивать наизнанку»). В противном случае полученный полиэдр геометрически совместим с исходным, но «перекрашен», по А. В. Шубникову (рис. 1).

Подчеркнём, что эверсия не тождественна инверсии: эвертированный полиэдр отличен от инвертированного противоположными ориентировками нормалей к граням. Таким образом, концепция антисимметрии логично следует из диссимметрии, не требуя привлечения «цвета» как физического свойства. Его роль играет ориентировка нормали к грани полиэдра, оставляя рассуждение в рамках геометрической кристаллографии.

Частично эвертированные полиэдры

Усложним задачу, разрешив перемещать на другую сторону от начала координат любое число граней исходного полиэдра на любые расстояния. Полученные полиэдры назовём частично эвертированными. Для примера рассмотрим те же тригональные трапецоэдр (32) и дипирамиду (6m2). Первый имеет лишь элементы симметрии 1-го рода, второй — 1-го и 2-го рода. Из тригонального трапецоэдра получим 63 комбинаторно различных полиэдра: один с шубниковской т.г.с. m', остальные классические 1 и 2. Из тригональной дипирамиды получим 36 комбинаторно различных полиэдров: три с шубниковски-ми т.г.с. 222, 2 и mm'2, остальные — классические 1, 2 и m. Изображения всех полиэдров даны в статье [15], с шубниковскими т.г.с. — на рис. 2. Как связаны т.г.с. полученных антисимметричных и исходных полиэдров?

Комбинированные полиэдры

Очевидно, одна часть граней антисимметричных полиэдров взята из граней исходного, другая — из граней эверти-рованного полиэдра. В целом антисимметричные полиэдры составлены из граней комбинированного (исходный плюс эвертированный) полиэдра, обладающего инверсионной шубниковской т.г.с. При этом исходный и эвертированный полиэдры гемиэдричны по отношению к комбинированному. Теперь ясно, что m — подгруппа шубниковской т.г.с. ди-тригонального скаленоэдра ( 3'т' ), порождаемого тригональным трапецоэдром, а 222 , 2 и mm2 — подгруппы шубниковской т.г.с. гексагональной дипирамиды ( 6/mmm ), порождаемой тригональной дипирамидой (рис. 3).

Заключение

Таким образом, концепция антисимметрии выводима не только из концепции симметрии добавлением цвета (физического свойства) фигуры, но и из концепции диссимметрии, где роль цвета играет ориентировка нормали к грани полиэдра. Такая трактовка интересна тем, что не выводит рассуждение о симметрии, диссимметрии и антисимметрии из области геометрической кристаллографии, позволяя ограничиться движениями граней вдоль

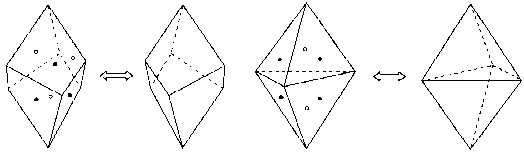
Рис. 1. Антисимметричный тригональный трапецоэдр (слева) и перекрашенная тригональная дипирамида (справа). Внутренние нормали показаны чёрными (на передних гранях) и белыми (на задних гранях) кружками, внешние нормали не показаны

Fig. 1. Antisymmetric trigonal trapezohedron (left) and trigonal dipyramid painted the opposite color (right). The internal normals are marked black (on front facets) and white (on back facets) circles, the external normals are not marked

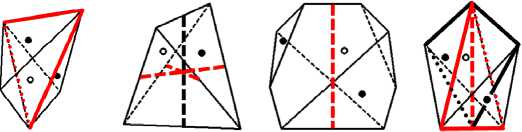
Рис. 2. Антисимметричные полиэдры, полученные из тригонального трапецоэдра (слева, m ) и тригональной дипирамиды (справа, 222 , 2 , mm2 ). Плоскости и оси антисимметрии показаны красным цветом

Fig. 2. Antisymmetric polyhedra derived from a trigonal trapezohedron (left, m' ) and a trigonal dipyramid (right, 222 , 2 , mm'2 ). The planes and axes of antisymmetry are marked red

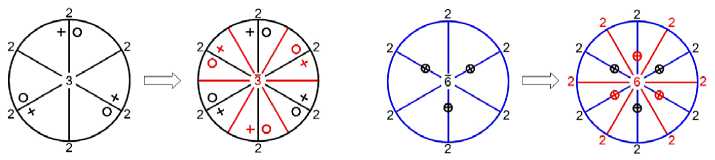
Рис. 3. Исходные, эвертированные и комбинированные выпуклые полиэдры на стереографических проекциях. Тригональный трапецоэдр (т.г.с. 32 ) порождает дитригональный скаленоэдр (т.г.с. 3’т’ , слева), тригональная дипирамида (т.г.с. 6m2 ) порождает гексагональную дипирамиду (т.г.с. 6/mmm ‘ , справа). Грани даны чёрными (исходные) и красными (эвертированные) крестиками (передняя полусфера) и кружками (задняя полусфера). Оси симметрии ( 2, 3, 6 ) и антисимметрии ( 2 , 3 , 6 ) показаны чёрными и красными цифрами, плоскости симметрии и антисимметрии — синими и красными линиями соответственно

Fig. 3. The initial, everted and combined convex polyhedra in the stereographic projections. A trigonal trapezohedron (s.p.g. 32) generates a ditrigonal scalenohedron (s.p.g. 3'm', left), a trigonal dipyramid (s.p.g. 6m2 ) generates a hexagonal dipyramid (s.p.g. 6'/mmm ‘, right). The facets are indicated by black (initial) and red (everted) crosses (front hemisphere) and circles (back hemisphere). The axes of symmetry (2,3, 6) and antisymmetry (2, 3,6) are marked black and red figures, while the planes of symmetry and antisymmetry are marked blue and red respectively нормалей. Рассуждения потребовали введения новых понятий: радикальной диссимметризации, (частично) эвер-тированного и комбинированного полиэдров, предлагаемых к обсуждению.

Авторы благодарят рецензентов за высокопрофессиональные замечания, способствующие развитию темы.

Работа частично выполнена в рамках темы НИР 02262019-0052 Геологического института КНЦ РАН.