Из опыта преподавания. III. Кристаллография икосаэдрических вирусов

Давно замечено, что природа рациональна. Структуры, оптимальные в том или ином физическом контексте, копируются в минеральных и живых объектах. Плоскости, простые и винтовые оси симметрии в организации минералов, животных и растений буквально бросаются в глаза. По меткому выражению Н. В. Белова, «осью 5-го порядка жизнь защищается от кристаллизации». Вокруг нас идет согласование эволюционных стратегий. Неудивительно, что в поле зрения кристаллографии попадает все больше структур, к описанию которых применимы математический язык теории симметрии и физические методы структурного анализа. Представляется правильным включать рассмотрение таких примеров в университетский лекционный курс.

Кристаллография живого вещества впервые и мощно заявила о себе расшифровкой структур ДНК и РНК Дж. Уотсоном и Ф. Криком в 1953 г. (Нобелевская премия 1962 г.). С тех пор теоретическим и приборными анализами охвачены разные живые объекты. В том числе нами показано широкое распространение в минеральной и живой природе полиэдрических структур типа фуллеренов, в которых разрешены только 5-угольные (ровно 12) и 6-угольные (все остальные) грани [5]. При этом в самых симметричных фуллеренах легко узнаваем додекаэдрический мотив, ведь простейший фуллерен — именно додекаэдр, а самый стабильный фуллерен Сбо — усечённый икосаэдр. В скелетах радиолярий встречены оба мотива (Circogonia dodecahedra Hackel и Circogonia icosahedra Hackel).

Но наиболее ярко они выражены в капсидах икосаэдрических (сферических) вирусов (рис. 1). Тот факт, что додекаэдр и икосаэдр геометрически дуальны друг другу, позволяет легко перейти от одного к другому и дать классификацию и номенклатуру для всех структур на их основе. «Номенклатура и классификация вирусов — трудная область вирусологии... Группировка может быть основана на морфологических и физиологических критериях. Идеал, к которому мы стремимся — это создать такую классификацию, которая отражала бы эволюционные и филогенетические взаимоотношения организмов, а также обеспечивала бы удобную и рациональную систему номенклатуры» [1, с. 18—23]. В части морфологии икосаэдрических вирусов задачи классификации и номенклатуры решаются в предлагаемой статье.

Принципы классификации и номенклатуры

Принципы строения капсидов икосаэдрических вирусов из капсомеров (субъединиц, сферических белковых глобул) и их классификация предложены ранее [3]. Всякий капсид (белковая оболочка, в которую упакована свернутая в клубок молекула ДНК или РНК) построен из 20 равносторонних треугольных мегаграней — фрагментов плоской сетки, образованной гло-

Гексоны (всего 20)

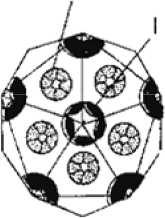
Пентоны (всего 12)

Полые шипы на вершинах икосаэдра

путем протеолиза

Фибриллярные отростки

Капсид содержит

12 пеятонов i по одному на каждую вершину) и 240 гексонов

Неустановленное число капсомеров на гранях

Удаление наружного капсида

РЕ08ИРУС (55-60 нм, вирус животных}, показаны наружный и внутренний капсиды

АДЕНОВИРУС        Поперечный срез аденовируса,

160—90 нм, вирус животных) гюказывающии расположение ДНК

Протомер, или белковая субъединица

Рис. 1. Строение икосаэдрических вирусов [2]

Fig. 1. The structure of icosahedral viruses [2]

булами по принципу плотнейшей шаровой упаковки. Линии глобул не всегда совпадают с рёбрами икосаэдра, что и создавало проблему поиска общей формулы для их числа в капсиде.

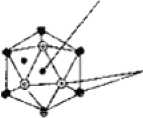
В статье [3] анонсирована теорема, перечислившая разрешённые для икосаэдрических капсидов «триангуляционные числа» Т = Pf2, где Р = h2 + hk + k2, h > k > 0 — любые пары целых чисел без общих делителей (при этом h > 0, т. к. h = 0 влечет k = 0, что противоречит физическому смыслу триангуляционного числа как площади грани капсида), f = 1, 2, 3... Доказательство впервые приведено в статье [4, с. 1124—1125]. По сути, h и k — координаты конца базального ребра мегаграни в косоугольной (60°) декартовой системе координат, согласованной с плотнейшей упаковкой глобул (рис. 2).

В основу описания икосаэдрических капсидов сегодня положены именно триангуляционные числа Т (табл. 1). В этом есть известное удобство. Число глобул в капсиде: М = 10Т + 2. Они образуют морфологические субъединицы: 12 пентамеров и 10(Т — 1) гексамеров. При этом Т = (m — 1)2, где m — число глобул на ребре мегаграни, т. е. если линия глобул и ребро икосаэдра сонаправлены (верхняя строка табл. 1, класс (f, 0), см. далее) [6]. Кроме того, 20Т — число элементарных треугольных граней у любого капсида. Для многих вирусов эти характеристики известны: бактериофаг фХ174: Т = 1, M = 12, m = 2, (h, k) = (1, 0); вирус жёлтой мозаики турнепса: Т = 3, M = 32, (h, k) = (1, 1); вирус полиомы: Т = 4, M = 42, m = 3, (h, k) = (2, 0); паповавирус: Т = 7, М = 72, (h, k) = (2, 1); реовирус: Т = 9, M = 92, m = 4,

(h, k) = (3, 0); ротавирус: Т = 13, М = 132, (h, k) = (3,1); вирусы герпеса и ветряной оспы: Т = 16, M = 162, m = 5, (h, k) = (4, 0); аденовирус и вирус собачьего гепатита: Т = 25, M = 252, m = 6, (h, k) = (5, 0); радужный вирус: Т = 81, M = 812, m = 10, (h, k) = (9, 0). Анализ таблицы обнаруживает изомеры — вирусы с одинаковым Т. Для Т = 49 их можно различить по симметрии: капсид (h, k) = (7, 0) имеет точечную группу симметрии (т. г. с.) — 5 - 3m , капсид (5, 3) — т. г. с. 532 . * Но для Т = 91 оба капсида (9, 1) и (6, 5) имеют т. г. с. 532 . Символ (h, k) фиксирует строение любого капсида однозначно. Именно его следует положить в основу номенклатуры.

Гомологические сериив классах —5—Зм и 532

В статье [3, с. 15, табл. 1] предложено деление икоса-эдрических капсидов на три класса. Первый (верхняя строка табл. 1) порождается простейшим капсидом (1, 0) — икосаэдром, в вершинах которого расположены белковые глобулы. Остальные капсиды класса, все с т. г. с. – 5 – 3m , получаются увеличением грани икосаэдра с помощью коэффициентов подобия f = 2, 3, 4… при той же ориенти-

Таблица 1. Триангуляционные числа T Table 1. Triangulation numbers T

k\h	1	1 2 1	1 3 1	1 4 1	1                5               |	1 6	7	8 1	1 9 1	1 10
0	1	4	9	16	25	36	49	64	81	100
1	3	7	13	21	31	43	57	73	1 91 1	1 111
2		12	19	28	39	52	67	84	103	124
3			27	37	1 49 1	63	79	97	117	139
4				48	61	76	93	112	133	156
5					75	1 91 1	109	129	151	175
6						108	127	148	171	196
7							147	169	193	219
8								192	217	244
9									243	271
10										300

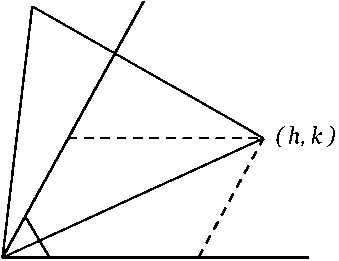
Рис. 2. Положение грани капсида (равносторонний треугольник) относительно линии глобул (горизонтальная ось h )

Fig. 2. The position of the capsid facet (equilateral triangle) relative to the line of globules (horizontal axis h )

ровке относительно плотнейшей упаковки глобул (рис. 2). Этот класс логично обозначить (f, 0). Судя по имеющимся публикациям (к сожалению, публикуются не первичные снимки высокого разрешения, а раскрашенные модели), короновирус SARS-CoV-2 (табл. 2, врезка) имеет капсид (2, 0), Т = 4, аналогичный вирусу полиомы. Это второй капсид в классе Т = f2, начинающемся с (1, 0) — бактериофага ϕX174. За SARS-CoV-2 следуют: (3, 0) — реовирус, (4, 0) — вирус герпеса и ветряной оспы, (5, 0) — аденовирус и вирус собачьего гепатита, … (9, 0) — радужный вирус.

Второй класс (диагональ табл. 1) порождается аналогичным преобразованием подобия из капсида (1, 1) — додекаэдра, над гранями которого надстроены пентагональные пирамиды. Его можно обозначить (f, f). Капсиды этого класса тоже имеют т. г. с. — 5-3m. Остальные капсиды (внутри треугольника в табл. 1) имеют только поворотные оси, то есть т. г. с. 532. Судя по тому, что они названы в статье [3] skew classes (скошенные, асимметричные классы), каждый символ (h, k) означает отдельный класс, в каждом — один капсид. Это не логично, так как преобразованием подобия любой капсид порождает бесконечную серию одинаково устроенных капсидов: (h, k) ^ (fh, fk)... Табл. 1 вся состоит из таких серий, начинающихся с (h, k), у которых h и k не имеют общих делителей.

Табл. 1 содержит и более интересные связи. Капсид (1, 1) получается из (1, 0) как усечённый икосаэдр из додекаэдра — дуальным переходом и отсечением всех вершин. Как это выразить алгебраически? На целочисленной решётке (рис. 2) рёбра (h_b k 1 ) и (h₂, k₂) двух капсидов выражаются друг через друга линейно. Пусть искомое преобразование имеет вид: (h 1 , k 1 ) ^ (h₂, k₂) = (ah 1 +bk 1 , ch 1 +dk 1 ). В статье [6] показано, что оно утраивает триангуляционное число. Из условия Т₂ = 3Т 1 находим, что для любого (h_b k_x) оно разрешимо лишь в случае: (h 1 , k 1 ) ^ (h₁+2k₁, h₁-k₁). Подстановкой легко убедиться в переходах (f, 0) ^ (f, f) ^ (3f, 0) ^ (3f, 3f). Тем самым две серии (f, 0) и (f, f) объединяются в класс — 5 - 3m (рис. 3, соединения 16-48- ..., 25-75... и др. подразумеваются). Аналогично объединяются в классы 532 пары (гомологические по отношению друг к другу) серий, образованных skew -капсидами (h, k) и (h + 2k, h - k). Читатель легко сделает это самостоятельно с помощью табл. 1. При этом капсиды (h, k), не сводимые к более простым, названы нами генераторами. Их критерий: h и k взаимно просты, h - k не делится на 3 (табл. 2). Заметим, что изомеры существуют и среди генераторов.

Общее преобразование капсида

Нельзя ли найти преобразование капсида в любой другой: (h_b k_x) ^ (h₂, k₂) — как это сделано для фуллеренов, моделирующих микроэволюции скелетов радиолярий [7]? По сути, задача состоит в повороте вектора (h 1 , k 1 ), образующего угол а 1 с осью h, до вектора (h₂, k₂), образующего угол а₂ с осью h, и дополнительном растяжении/сжатии (рис. 4). В ортогональной декартовой системе координат преобразование имеет вид:

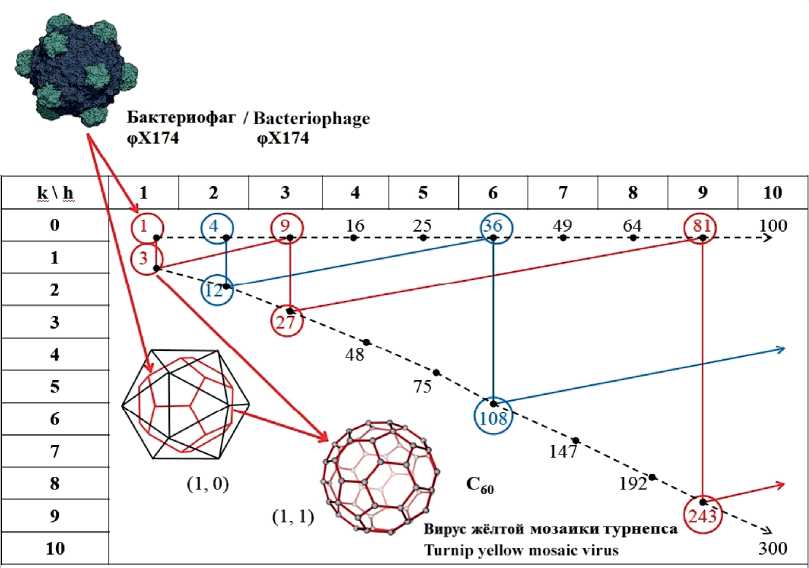
Рис. 3. Связь двух гомологических серий - 5 - 3m

Fig. 3. The relationship of two homologous series - 5 - 3m

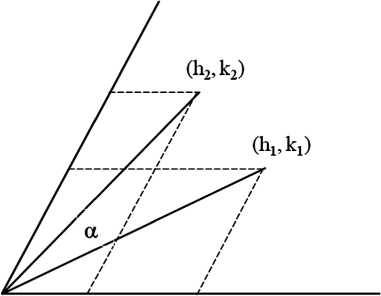
Рис. 4. К описанию общих преобразований икосаэдриче-ского капсида

Fig. 4. To the description of general transformations of an icosahedral capsid

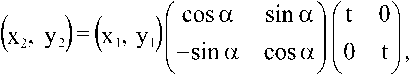
Таблица 2. Триангуляционные числа T для капсидов-генераторов

где a = a₂ — a i , коэффициент растяжения t = (T₂/T 1 )^1/2.

Формулы перехода к косоугольной (60°) системе координат: X i = T 1 ^1/2 cosa 1 , У 1 = T 1 ^1/2 sina_b x₂ = T₂^1/2 cosa₂, y₂ = T₂^1/2 sina₂. Выражаем тригонометрические функции через стороны треугольников (рис. 4) и после преобразований получаем:

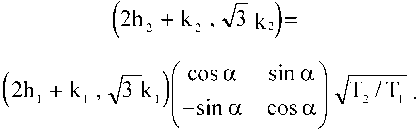
Задав (h 1 , k 1 ) и (h₂, k₂), находим коэффициент растяжения (T₂/T 1 )^1/2 и угол 0 < a < 60°.

Рассмотренные выше частные случаи следуют из полученного уравнения. Для преобразований подобия (h 1 , k 1 ) ^ (h₂, k₂) = (f h 1 , f k 1 ) подстановкой получим, что матрица поворота единичная: cos a = 1, sin a = 0, то есть a = 0. Действительно, указанные серии объединяют капсиды с гранями, одинаково ориентированными в системе координат (рис. 2). Для переходов между гомологичными сериями (h 1 , k 1 ) ^ (h₂, k₂) = (h 1 +2k_b h₁—k₁) находим общее решение: a = arc sin [^ — 3k 1 (h₁+k₁) / 2T 1 ]. При k 1 = 0, a = 30°, при k 1 = h 1 , a = -30°; в обоих случаях коэффициент растяжения равен A 3.

Действительно, в дуальных преобразованиях последовательные переходы отличаются лишь знаком поворота.

Выводы

Икосаэдрические вирусы — весьма содержательный объект кристаллографического, комбинаторно-геометрического и алгебраического исследования. Сегодня неясно, какие из вирусов, теоретически упорядоченных в табл. 1 и 2, реально действуют в природе. Их многообразие должно ограничиваться размерным фактором. Но уже очевидна важная роль капсидов (1, 0), (2, 1) и (3, 1), стоящих в начале таблицы, не сводимых к более простым, а наоборот, продуцирующих (в морфологическом смысле) двумя указанными способами (преобразованием подобия и дуальным переходом к гомологической серии) подавляющую часть известного многообразия. В поисках способов разрушения капсидов следует обратить на них особое внимание.

Описывает ли найденное выше общее преобразование капсидов реальный процесс? Нам это неизвестно. Но можно задать вирусологам связанный вопрос: сопровождаются ли мутации коронавирусов изменением длины свернутой в капсиде ДНК/РНК? Если да, то из соображений целесообразности, с очевидностью, воплощенной природой в структуре капсида, следует ожидать, что вирус подгоняет его под необходимый объем содержимого. Возможно, здесь кроется лазейка для разрушающего физического/химического воздействия на механизм построения капсида мутирующего вируса. Из выполненного исследования можно сделать выводы.

• •    Номенклатуру икосаэдрического капсида следует строить на символе (h, k) его икосаэдрической грани, однозначно фиксирующем её ориентацию относительно плотнейшей упаковки белковых глобул.

• •    Классификация капсидов по т. г. с. — 5 - 3т (с плоскостями) и 532 (без них) логична. Но класс —5—3т состоит из двух гомологических серий (f, 0) и (f, f), где f = 1, 2, 3..., связанных дуальным переходом (h 1 , k 1 ) ^ (h 1 + 2k 1 , h 1 — k 1 ).

• •    Класс 532 тоже состоит из серий (f h, f k), порождаемых генераторами (h, k), узнаваемыми по критерию: h и k взаимно просты, h — k не делится на 3. У каждой серии в классе есть гомологичная, связанная дуальным переходом (h 1 , k 1 ) ^ (h 1 + 2k 1 , h 1 — k 1 ).

• •    Предположительно, коронавирус SARS-CoV-2 имеет капсид (2, 0), т. г. с. —5—3т , Т = 4, аналогичный 43

  
  
  

вирусу полиомы, второй в серии гомологов Т = f2, порождаемой генератором (1, 0) — бактериофагом фХ174. Его эффективность определена не специфической морфологией, а функциональными особенностями.

• •    Получено общее преобразование, описывающее переходы (h₁, k₁) → (h₂, k₂). Икосаэдрические капсиды — редкий случай биологической организации, когда удалось получить столь общий результат, даже если он имеет лишь теоретическое значение.

• •    Представляет интерес следующая задача: частота встречаемости икосаэдрических вирусов классов — 5 - 3m и 532 , в частности различных видов (h, k), ещё детальнее — вирусов-изомеров.