Из опыта преподавания. IV. Три вопроса из курса кристалломорфологии

Вопросы, рассмотренные в статье, были заданы автору во время лекций по кристалломорфологии. Первый касается некоторых условностей в структуре таблицы 32 видов симметрии (в. с.) как она дана в университетском учебнике [2, с. 92], и трудностей с выводом инверсионных видов симметрии. Последовательный разбор исторической статьи [1] ставит все на место и напоминает о плодотворной деятельности Федоровского института* в стенах Ленинградского горного института (ныне Санкт-Петербургского горного университета).

Второй вопрос вызвал в аудитории откровенно любопытные взгляды: «Вы сказали, что простых форм 47, а я прочел в Интернете, что их 48. Как же так?» Пришлось тут же извлечь из Интернета ответ — статью А. К. Болдырева «47 или 48 простых форм возможны на кристаллах?» [5] (здесь и далее перевод наш). Она замечательно показывает важность строгих определений, в данном случае — определения простой формы (п. ф.).

Третий вопрос — о символах граней тригональных и гексагональных кристаллов в их гексагональной установке. В учебнике [2] рассмотрены случаи, когда след грани в горизонтальной (то есть перпендикулярной главной оси) плоскости параллелен или перпендику- лярен (рис. 125) одной из осей, и сделан вывод: сумма трех первых индексов всегда равна нулю. Но откуда следует, что всегда? Доказательство этой теоремы элементарно, его следует давать в лекциях.

История науки — составная часть самой науки. История кристаллографии богата поучительными сюжетами и коллизиями. Их использование в лекциях представляется полезным методическим приемом.

Таблица 32 видов симметрии

Вывод в. с. кристаллов, то есть возможных сочетаний допустимых элементов симметрии, выполняется в два этапа: для кристаллов с единичными направлениями Е (низшие и средние сингонии, 27 в. с.) и без них (кубическая сингония, 5 в. с.) [2]. Мы ограничимся лишь первым этапом. В качестве методического приема найдем возможные сочетания «очевидных» элементов симметрии (в обозначениях Федоровского института): осей L1, L2, L3, L4, L6, плоскости Р и центра инверсии С. Это позволяет показать, как возникает необходимость в «неочевидных» инверсионных осях и как они способствуют упорядочению таблицы 32 в. с.

Найдем сочетания единичного направления Е с элементами симметрии, сохраняющие Е. Совмещая с Е каждую из L n , получим «примитивные» в. с.: L 1 , L 2 , L 3 , L 4 , L₆ . Помещая С на Е, получим в. с. С . Проводя Р через Е или перпендикулярно к Е (И. И. Шафрановский обозначает их Р и П, но различает лишь в оперативных

целях; при подсчетах элементов симметрии Р = П) получим в. с. Ð . Ось L₂, перпендикулярная к Е, также сохраняет Е. Считаем этот в. с. совпадающим с примитивным (по аналогии с Р и П).

К каждой L_n добавим С. В силу известной теоремы для четных осей получим дополнительные перпендикулярные P: L₂PC , L₃C , L₄PC , L₆PC — «центральные» в. с. Те же в. с., кроме L₃Ð , получим, если к каждой из L_n добавим П.

К каждой L_n добавим продольную Р. В силу известной теоремы получим дополнительные Р: L₂2P , L₃3P , L₄4P , L₆6P — «планальные» в. с.

К каждой L_n добавим перпендикулярную L₂. В силу известной теоремы получим дополнительные L₂: 3L₂ , L₃3L₂ , L₄4L₂ , L₆6L₂ — «аксиальные» в. с.

К каждой L_n добавим С и продольную Р. В силу известных теорем получим дополнительные L₂ и Р: 3L₂3PC , L₃3L₂3PC , L₄4L₂5PC , L₆6L₂7PC — «планак-сиальные» в. с.

К оси L₃ добавим Р и П, получим новый в. с. L₃3L₂4P .

Таким образом, сочетания L_n, Р и С дают 25 из 27 в. с. (еще раз заметим, что 5 в. с. кубической сингонии здесь не рассматриваются), в том числе 5 хорошо выраженных классов (отвечающих столбцам таблицы) и стоящие отдельно в. с. L₃Р и L₃3L₂4P. Именно анализ комбинации L₃Р (а точнее L₃П в обозначении И. И. Шафрановского) позволяет узнать в ней новый элемент симметрии — инверсионную ось L_i6. Тут же встает вопрос о L_in других порядков^*. Легко увидеть, что L_i1 = C, L_i2 = P, L_i3 = L₃C и что инверсионная ось L_i4 никак не проявила себя ранее в сочетаниях «очевидных» элементов симметрии. Зато сама она и ее сочетание с Р и перпендикулярной L₂ дают два новых в. с.: L_i4 и L_i42L₂2P . Становится понятным, почему инверсионная ось L_i4 и два последних в. с. упущены даже в «Кристаллографических этюдах» О. Браве [3, с. 124].

Итак, все виды симметрии найдены, некоторые даже повторно. В какие ячейки таблицы их поместить? Статья [1] замечательно показывает накал международной дискуссии и аргументацию разных авторов. Так, «прибегать к сложным представлениям об инверсионных осях следует только в том случае, если никакого другого более простого толкования нельзя найти» [1, с. 153]. Именно поэтому в обозначениях большинства в. с. мы сегодня пользуемся символами С и Р, а не Li1 и Li2. Но их инверсионная подоплека оказалась весьма полезной: к триклинной сингонии логично отнесены в. с., в которые входит L1 или Li1; к моноклинной — в. с., в которые входит одна L2 или Li2. Перечислим условности в организации таблицы: С = Li1, Р = Li2, L3C = Li3 можно непротиворечиво отнести к инверсионно-примитивным; L2 — к примитивным, L2РС — к центральным в. с. За дополнительной аргументацией отсылаем читателя к статье [1].

47 или 48 простых форм?

Поводом к написанию статьи [5] послужила вышедшая накануне статья [6], автор которой предложил свои названия для п. ф. Сотрудниками Федоровского института эта работа была выполнена под руководством А. К. Болдырева 10 годами ранее [4]. Можно представить, какой интерес вызвала статья [6] даже не расхождениями в названиях п. ф., а тем, что их оказалось 48, а не 47. А. К. Болдырев замечает, что можно иметь различные мнения относительно названий, но не числа п. ф. Полагать, что их 48, а не 47 — это не мнение, а ошибка, как и считать, например, что в. с. 33, а не 32.

Причина дискуссии — диэдр, который оказался разделенным на «дому» (планальный диэдр, в. с. m ) и «сфеноид» (осевой диэдр, в. с. 2 ). Чтобы разрешить противоречие, А. К. Болдырев начинает с определения: две п. ф. различны, если у них различное число граней или если последние различаются формой или взаимным расположением^**. В противном случае они суть одна п. ф., даже если получены из исходной грани различными операциями симметрии. Далее он показывает, что А. Ф. Роджерс в целом следует тому же определению, называя пинакоидом пару параллельных граней в любом (где он разрешен) в. с.; ромбической призмой — п. ф. {hk0} и {hkl} в ромбической и моноклинной сингониях; октаэдром — п. ф., полученную в центральном и аксиальном в. с. кубической сингонии с помощью разных элементов симметрии (Р и С в первом случае, оси симметрии — во втором); аналогично — тетрагональные призмы разных в. с., дипирамиды разных сингоний и т. п., и только для диэдра делает исключение, различая «дому» и «сфеноид», что непоследовательно и нелогично.

По сути, этой аргументацией дискуссия вполне исчерпывается. Что касается названий 47 п. ф., то 32 из них совпадают, 15 различаются (3 — в низших, 2 — в средних, 10 — в кубической сингонии). Время показало, что конструктивный и единообразный подход (главным образом для п. ф. кубической сингонии), предложенный сотрудниками Федоровского института, оказался удобным и ныне принят большинством научных школ.

Символы простых форм

На основании теоремы синусов из малого и большого треугольников (рис. 1) имеем соотношения:

1/sin (120 – α) = a / sin α,

1 / sin (60 – α) = b / sin α, откуда следует:

a = sin α / sin (120 – α), b = sin α / sin (60 – α).

Взяв обратные величины к длинам отрезков, отсекаемых гранью АВ на осях координат (с учетом знаков: 1, b , – a ), и избавляясь от дробей умножением на sin α (который, очевидно, не равен нулю), получаем три ее первых индекса: sin α, sin (60 – α), –sin (120 – α). С помощью тригонометрических формул находим:

sin α + sin (60 – α) — sin (120 – α) =

= 2 sin (a — 60) x cos 60 + sin (60 — a) =

= sin (α – 60) + sin (60 – α) = 0.

Итак, сумма равна нулю для любого α, то есть для любой грани кристалла тригональной или гексагональной сингонии.

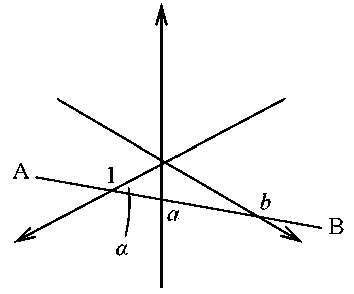
К доказательству теоремы. При α = 60 и 30° получим рис. 125 а, б из учебника [2]

To the proof of the theorem. For α = 60 and 30° we get Fig. 125 a, b [2]

Заключение

Вывод 32 видов симметрии кристаллов, как правило, увлекает студентов, если подать тему с должным историко-научным экскурсом, не забыв упомянуть, что И. И. Шафрановский до конца своих дней искал тайный подтекст этого замечательного числа — пятой степени двойки. Догадка о возможности и необходимости инверсионных осей симметрии при описании кристаллических полиэдров впечатляет студентов не меньше, чем «основная теорема кристаллографии» о невозможности L5, L7 и т. д. Вывод 32 видов симметрии математически несложен (особенно когда ответ известен), требует лишь внимания и знания нескольких вполне наглядных теорем. Но перебор сочетаний элементов симметрии допускает варианты, что оживляет рутинные процедуры. Неоднократное обращение к таблице 32 видов симметрии в ее современной форме способствует усвоению терминологии. Поначалу примитивные в. с. путаются с аксиальными — те и другие суть сочетания осей симметрии; некоторые центральные в. с., состоящие из осей, плоскостей и центра инверсии, путаются с планаксиальными и т. д. Наконец, классифи- кация, номенклатура и символика 32 в. с. кристаллов, как и номенклатура 47 п. ф., — замечательные результаты российских кристаллографов, признанные в мире. Об этом уместно и необходимо упоминать в лекциях.

Автор благодарит рецензентов за профессиональные советы, способствовавшие более четкому изложению материала.