Из опыта преподавания. VI. Симметрия бордюров

В университетском курсе кристаллографии для геологов широкого профиля [4] переход от конечных фигур и 32 точечных групп (видов) симметрии (т. г. с.) к бесконечным фигурам и 230 пространственным (федоровским) группам симметрии (п. г. с.) совершается очень быстро. Теорема о порождении однородных элементов симметрии при взаимодействии плоскостей и осей симметрии с ортогональными трансляциями иллюстрируется по ходу вывода всего 2—3 простейших п. г. с. Теория 230 п. г. с. остается в сознании большинства студентов недоступной абстракцией. Рекомендуемые для самостоятельного изучения работы [1, 2] остаются нетронутыми. Об этом писал Н. В. Белов в предисловии к книге [3].

«Вторая глава раздела геометрической кристаллографии посвящена “внутреннему устройству кристаллов”, т. е. 14 решеткам Бравэ и 230 федоровским группам. Опыт показывает, что для того, чтобы эти объекты преподавать надлежащим образом, нужен специальный курс, в учебнике же более элементарной кристаллографии они всегда выглядят куцыми. <™> 17 плоских групп должны предшествовать 230 пространственным, чтобы на них была изучена симметрия бесконечных мотивов на обоях и тканях, обобщением которых будут все структурные мотивы трехмерных кристаллов. <™> На обойных (wallpaper — термин М. Бюргер. — Ю. В.) груп пах была бы изучена такая важная характеристика центрированных групп, как всегдашнее “чередование” элементов симметрии двух сортов: плоскостей зеркальных с плоскостями скольжения, осей поворотных с винтовыми и т. д. Что-то об этом, очевидно, должно быть сказано в элементарном курсе™» [3, с. 9—10].

В течение ряда лет автор использует для тех же целей еще более простой аппарат семи групп симметрии бордюров. Уже они иллюстрируют указанную теорему о порождении однородных элементов симметрии. Вывод семи типов бордюров относительно прост и вдохновляет студентов на последовательный штурм 17 плоских групп симметрии, 31 группы симметрии лент и даже 230 п. г. с.

Теория

Все семь типов бордюров популярно показаны и иллюстрированы А. В. Шубниковым. Он определяет бордюр как «фигуру без особенных точек, но с особенной полярной плоскостью и единственной осью переносов» [5, с. 72]. Полярная плоскость — это плоскость рисунка. И нас интересует лишь его лицевая сторона. А трансляция бордюра вдоль единственной оси переносов не оставляет ни одну точку неподвижной (особенной) в отличие от точечных групп симметрии при описании конечных фигур. Перед выводом типов бордюров следует ввести удобные обозначения элементов симметрии, например: Т — трансляция, T* — пло-

скость скользящего отражения (трансляционная составляющая у T* равна T/2), 1 — единичная операция, Р — продольная (сонаправленная Т) плоскость симметрии, П — поперечная к Т плоскость симметрии (обозначение И. И. Шафрановского для плоскости, поперечной к единичному направлению фигуры [4, с. 71]), С — центр инверсии (действует в плоскости рисунка как перпендикулярная к нему ось симметрии L 2 ).

Дальнейший вывод состоит в переборе сочетаний операций 1, Р, П, С, геометрически формирующих из элементарной асимметричной фигуры (обычно треугольник) кластер, и его размножении в бордюр операциями Т и Т*. Последовательность операций удобно обозначать произведением. Операции 1, Р, П, С перестановочны. Геометрически в этом легко убедиться при построении кластера. Алгебраически это следует из коммутативности произведения диагональных матриц. В тройке Р, П, С произведение любых двух операций дает третью.

Эти свойства делают перебор совсем простым и приводят к семи различным бордюрам: Т ( а , по [5]), Т* ( а ) РТ ( a m ), ПТ ( a : m ), СТ ( a : 2 ), РПТ ( a : 2 m ), ПТ* ( a’: 2 ) (рис. 1). Бордюр РПТ получается еще как РСТ, ПСТ и РПСТ, так как РП порождает С, РС — П, ПС — Р. В итоге все четыре содержат комбинацию элементов симметрии РПСТ. Аналогично бордюр ПТ* получается как СТ*, но взаимная ориентация треугольников в

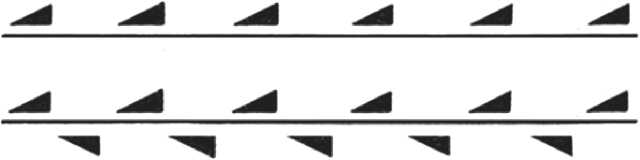
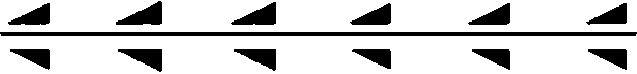
кластерах различна. В этом случае П взаимодействует с составляющей Р плоскости зеркального отражения Т* и дает С, а С взаимодействует с составляющей Р и дает П. В итоге оба бордюра содержат комбинацию элементов симметрии ПСТ* (рис. 2).

Заметим, что бордюр РТ* по внешнему виду совпадает с РТ. Но при фиксированной трансляции Т первый уложен кластерами в два раза чаще (рис. 3). Аналогично соотносятся бордюры РПТ* и РПТ (рис. 4). В бордюре РПТ* полезно обсудить со студентами двукратное появление дополнительных П и С из-за высокой симметрии транслируемого кластера в силу все той же теоремы о порождении однородных элементов симметрии. Наличие указанных разновидностей у бордюров ПТ*, РТ и РПТ обычно не отмечается.

Соподчинение групп симметрии бордюров можно показать двумя путями — вложением друг в друга их геометрических схем (рис. 1) и символов. Очевидно, что группа РПТ (РПСТ) находится в самом верху, Т — в низу иерархии. Вполне ясны вложения: РПТ (РПСТ) ^ РТ, СТ, ПТ ^ Т (рис. 5, слева), ПТ* (СТ*) ^ Т*, СТ, ПТ ^ Т (рис. 5, в центре) и РТ ^ Т* ^ Т. Объединяя их, получаем схему (рис. 5, справа).

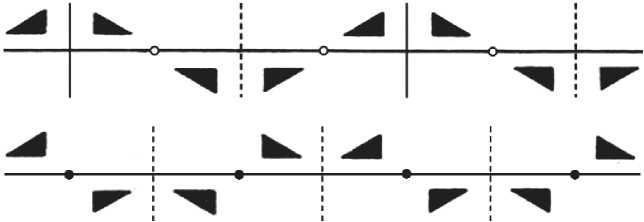
Рис. 2. Бордюры ПТ* (вверху) и СТ* (внизу) получены из того же элементарного треугольника (слева вверху). Вид симметрии тот же, но орнаменты различны

Fig. 2. The borders ПТ* (top) and СТ* (bottom) are obtained from the same elementary triangle (top left). The type of symmetry is the same, but ornaments are different

Рис. 3. Бордюры РТ (вверху) и РТ* (внизу)

Fig. 3. The borders РТ (top) and РТ* (bottom)

Рис. 1. Семь типов бордюров, сверху вниз: Т, Т*, РТ, ПТ, СТ, РПТ и ПТ*. Горизонтальная линия — направление трансляции Т, плоскостей Т* или Р (из контекста). Вертикальные сплошные линии и залитые кружки — П и С в кластере. Вертикальные штриховые линии и пустые кружки — П и С, порожденные трансляциями Т и Т*

Fig. 1. Seven types of borders, from top to bottom: Т, Т*, РТ, ПТ, СТ, РПТ, and ПТ*. The horizontal line is the direction of translation Т, planes Т* or Р (from the context). Vertical solid lines and filled circles are П and С in the cluster. Vertical dashed lines and empty circles are П and С generated by translations Т and Т*

Пример 1. Кириллица и латиница

Какие бордюры можно образовать, выписав подряд некоторую заглавную букву кириллицы или латиницы? Результат для кириллицы (в порядке убывания частот): тип Т — БББ. и др. (13 букв, 39.4 %), тип ПТ — ААА. и др. (8 букв, 24.3 %), тип РТ — ВВВ. и др. (7 букв, 21.2 %), тип РПТ — ХХХ... и др. (4 буквы, 12.1 %), тип СТ — ИИИ... (1 буква, 3.0 %). Результат для латиницы: тип Т — FFF. и др. (8 букв, 30.8 %), тип ПТ — ААА... и др. (6 букв, 23.1 %), тип РТ — ВВВ. и др. (5 букв, 19.2 %), тип РПТ — ХХХ. и др. (4 буквы, 15.4 %), тип СТ — ZZZ. и др. (3 буквы, 11.5 %). В обоих случаях типы Т* и ПТ* отсутствуют — плоскость зеркального отражения Т* перебрасывает букву на другую сторону, удваивая ее, что противоречит правилу построе- 29

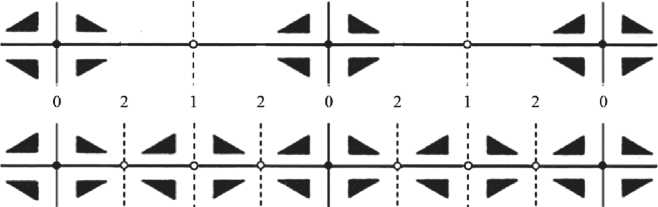
Рис. 4. Бордюры РПТ (вверху) и РПТ* (внизу). Плоскости П: 0 — в кластере, 1 — порожденные 1-го рода, 2 — порожденные 2-го рода

Fig. 4. The borders РПТ (top) and РПТ* (bottom). The planes П: 0 — in the cluster, 1 — generated of the 1^st kind, 2 — generated of the 2^nd kind

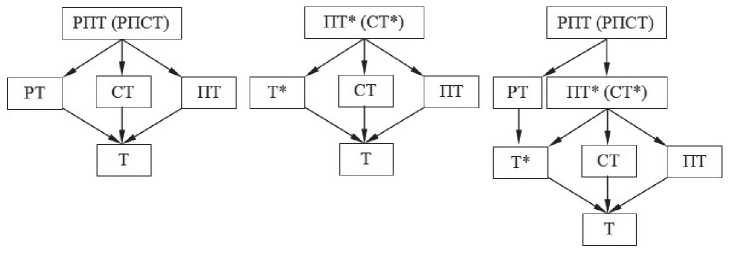
Рис. 5. Иерархия групп симметрии бордюров

Fig. 5. Hierarchy of border symmetry groups ния бордюра (написание букв подряд). Итак, частотные спектры типов бордюров для обоих алфавитов совпадают, что лишь отчасти объяснимо одинаковым начертанием некоторых букв. Этот совсем не минералогический пример не требует наглядных пособий и обращает внимание студентов на частотный анализ видов симметрии как метод исследования неограниченного многообразия объектов.

Пример 2. Архитектура

Студенты охотно замечают архитектурные бордюры в городском ландшафте (ограды, решетки, орнаменты, барельефы, горельефы, мозаики и т. д.), ищут в них асимметричные элементы, определяют виды симметрии бордюров и активно дискутируют. Это именно то, о чем мечтает каждый профессор. На рис. 6 дано по одному бордюру каждого вида симметрии. Но при сборе оказывается, что их разнообразие в каждом виде велико, при этом различно (по нашим данным, убывает в ряду ПТ, РПТ, СТ, Т, ПТ*, РТ, Т*). Возникает вопрос о замыслах архитекторов. В решетках мостов и набережных Невы част и уместен динамичный бордюр Т, подчеркивающий бег волн. Впрочем, в зданиях вдоль проспектов с потоками машин они смотрятся тоже неплохо. В лепных украшениях старинных государственных учреждений наиболее часты бордюры ПТ и РПТ, вертикальными плоскостями симметрии акцентирующие массивность зданий и тем самым незыблемость империи. Аналогично — в спальных районах, что вызывает ощущение покоя. Отсюда легко перебросить логический мостик к анализу «замыслов природы», заложившей (тоже с весьма разной частотой) 230 п. г. с. в структуры минералов.

Кристаллографический заряд архитектурных бордюров этим далеко не исчерпан. На рис. 7 (слева) в од- 30

ном архитектурном орнаменте сочетаются бордюры ПТ* и СТ, виды симметрии которых соотносятся как группа и подгруппа. Но их трансляции не согласованы, что позволяет упомянуть в лекции о несоразмерных фазах как минералогических аналогах. Там же показано, как бордюр Т с цветками двух сортов накладывается на бордюр-лиану Т* вдоль общей линии трансляции с образованием единого бордюра Т. Кристаллографическая аналогия — суперпозиция нескольких правильных си-

Рис. 6. Семь типов бордюров в архитектуре Санкт-Петербурга, сверху вниз: Т, Т*, РТ, ПТ, СТ, РПТ и ПТ*

Fig. 6. Seven types of borders in the architecture of Saint Petersburg, from top to bottom: Т, Т*, РТ, ПТ, СТ, РПТ, and ПТ*

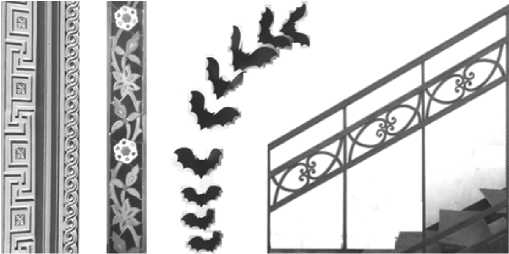
Рис. 7. Сочетания бордюров, криволинейный и однородно деформированный бордюры

Fig. 7. Combinations of borders, curved and uniformly deformed borders стем точек в структуре минерала. Бордюр РТ (летучие мыши) с искривленной линией трансляции явно напоминает о криволинейной симметрии и симметрии подобия Д. В. Наливкина и П. Л. Дубова. Наконец, однородно деформированный бордюр ПТ вдоль лестничного марша (рис. 7, справа) отсылает нас к гомологии В. И. Михеева. Но эти обобщения симметрии классических бордюров в архитектуре и минералогии заслуживают отдельного рассмотрения.

Заключение

«Книга И. Костова — весьма хороший курс для высшей школы, его перевод будет иметь важное значение не только сам по себе, но и поможет встряхнуть застывшие советские курсы кристаллографии и, может быть, напомнит их составителям о необходимости большего внимания и к нашим классикам, и к зарубежным кристаллографам» [3, с. 14]. Сказано смело и должно пониматься не в том смысле, что «советские курсы кристаллографии» плохи * , а в том, что для максимально доступного изложения трудного курса кристаллографии надо использовать лучшие методические приемы, найденные отечественными и зарубежными профессорами. Иначе для большей части студентов-геологов, не имеющих склонности к математике и не избравших кристаллографию своей специализацией,

230 п. г. с. навсегда останутся величественной, но пугающей глыбой теории. А ведь они должны быть надежным руководством в изучении минерального мира, да и всего универсума. Как показано выше, вывод семи видов симметрии бордюров богат нюансами, подготавливающими студентов к освоению 230 п. г. с. А окружающая природа, городские ландшафты и произведения искусства изобилуют образцами, превращая математическую теорию в действенный инструмент познания мира, позволяя «поверить алгеброй гармонию» и всякий раз побуждая к размышлениям о замыслах архитектора.

Автор благодарит студентов Санкт-Петербургского горного университета С. И. Азаренко, А. А. Дирксен, А. С. Иванову, К. П. Мальцеву, Е. А. Потанину, С. В. Шовкун за помощь в сборе архитектурных бордюров и обсуждение темы.