Из опыта преподавания. XII. Зарождение кристалла и принцип равного ближайшего окружения

Иногда студенты задают неудобные вопросы. Проблема преподавателя состоит в том, что ответ должен быть убедительным и лаконичным. Длинный не пройдет: долго объясняете — знать, неясно мыслите. Что вообще означает — «объяснить»? Этимологически — сделать ясным, по сути — свести сложное к простому, непонятное — к уже понятому. Но кого-то убеждают расчеты, другого — геометрические образы. Да и сам преподаватель имеет предпочтения. Здесь есть педагогическая проблема. Вот вопрос студента-геолога на излете 2-го курса: «Согласно какому наглядному принципу рождается кристалл, если коротко? У Ч. Банна я ответа не нашел». Вопрос обескураживает. Книга (Банн, 1970), рекомендованная мной, — хороший ориентир. Значит, некогда популярная, она уже не обладает нужной строгостью. Укажем во избежание недоразумений, что фундаментальное объяснение зарождению, росту и превращениям кристаллов может дать только термодинамика (Темкин и др., 1980) в альянсе с кристаллохимией (Филатов, Пауфлер, 2019). Система (расплав, раствор) всякий раз замыкает химические связи в узилище кристаллической решетки ради минимизации свободной энергии. Далее речь пойдет о наглядном образе, иллюстрирующем физический принцип при образовании зародышей.

Принцип равного ближайшего окружения

Поищем образ в геометрии. При этом будем иметь в виду, что в себе самой она движения не содержит. В сценарий рождения кристалла его приходится вводить как смену атомных конфигураций, выражающих на каждом шаге некую целесообразность. Но в чем она? Суть кристалла — в трансляционной упорядоченности, точнее — в суперпозиции правильных систем точек, по которым распределены кристаллохимически эквивалентные атомы. Более строго — точеч-

ная (r, R)-система Делоне будет кристаллом, если она орбита некоторого конечного множества по пространственной группе G. Система Делоне называется правильной, если она G-орбита одной точки. В этом случае все точки равно окружены другими (Галиулин, 1984).

Для дальнейшего кажется разумным принцип равного ближайшего окружения. Но как он реализуется в конечной структуре? Пусть куб с ребром n сложен единичными кубиками. Их число N распределено по позициям: N = n3 = (n – 2)3 + 6(n – 2)2 + 12(n – 2) + 8, где первое слагаемое — число центральных, второе — центральных гранных, третье — центральных реберных, последнее — вершинных кубиков. С n быстрее всего растет число центральных, но даже для n = 10 их всего 512, т. е. чуть больше половины. «Почти все» (95 %) кубики станут центральными при n = 118, когда в кубе их будет N = 1 643 032, т. е. более 1.64 миллиона. Принцип, принимаемый в целом, проявляет себя далеко не сра- зу. Тем более интересно, что для совсем малых кластеров он дает нетривиальные результаты.

Рост малых кластеров из сферических частиц смоделирован в работе (Дубов и др., 1995). Для полиэдрических форм ее превосходят лишь компьютерные каталоги выпуклых 4- … 12- и простых (3-валентных) 13- … 16-эдров (Войтеховский, Степенщиков, 2008a, 2008b). Дуальным переходом из них получаются полиакроны (поливершинники). Рисунок 1 показывает сложность моделирования — быстро нарастающее разнообразие кластеров. Выявление трендов упрощается, если учесть принцип равного ближайшего окружения. В идеале ему удовлетворяют лишь платоновы и архимедовы полиэдры, призмы и антипризмы. (Нас не интересует квазидвумер-ный случай, для которого годятся кольца и зигзаги — тренд вверху справа на рис. 1.) Это условие принимают и другие авторы (Aslanov, Markov, 1989; Aslanov, 1991).

Перечислим подходящие конфигурации малых кластеров: мономер (N = 1), димер (2), треугольник (3),

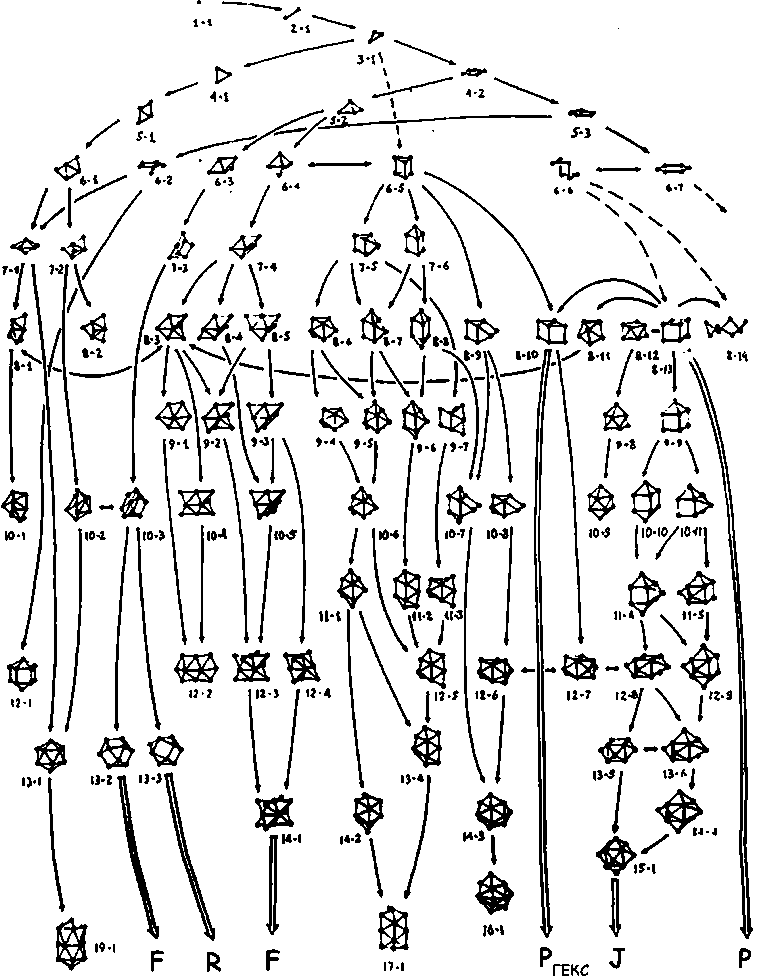
Рис. 1. Схема формирования кластеров с ростом N (Дубов и др., 1995, рис. 1.7)

Fig. 1. Scheme of cluster formation with increasing N (Dubov et al., 1995, Fig. 1.7)

тетраэдр (4), октаэдр и 3-гональная призма (6), куб и 4-гональная антипризма (8), 5-гональные призма и антипризма (10), усеченный тетраэдр, архимедов кубооктаэдр и икосаэдр (12). Они отсутствуют для нечетных N = 5, 7, 9, 11. Для N = 5 есть всего два полиэдрических кластера — 3-гональная бипирамида и 4-го-нальная пирамида (5-1 и 5-2 на рис. 1). В статье (Войтеховский, 2022) для сравнения выпуклых полиэдров дополнительно к точечной группе симметрии (т. г. с.) и порядку группы автоморфизмов (п. г. а.) предложено использовать статистические энтропии разнообразия вершин H_v и ребер H_e. Для 3-гональной бип и рамиды (т. г. с.^* L_i63L₂3P = L₃3L₂4P = L₃3L₂3PП = D_3h = = 6 m2, п. г. а. 12, H_v = 41.8 % от max^**, H_e = 29 % от max) и 4-гональной пирамиды (L₄4P = L₄2P2P’ = C_4v = 4mm, п. г. а. 8, H_v = 31.1 % от max, H_e = 33.34 % от max) они показывают двойственную ситуацию. У 3-гональной бипирамиды выше п. г. а. и ниже H_e, у 4-гональной пирамиды ниже H_v. Что выгоднее? Легко представить, как 5-атомный кластер колеблется, выбирая между ними. По сути, он находится с некоторыми вероятностями сразу в двух состояниях.

Возникает догадка: 5-атомный кластер присоединяет еще 1 атом и принимает самую симметричную (из кристаллографических) 8 -эдрическую конфигурацию (3L₄4L₃6L₂9PC = O_h = m3m, H_v = H_e = 0). Иначе говоря, он переходит из 4-эдрической (N = 4) сразу в 8-эдрическую (N = 6). Так же преодолеваются конфигурации с N = 7, 9, 11. И в этих случаях выбор идет между кластерами в виде бипи р амид и пирамид: N = 7 — 5-гональная бипирамида (10m2, п. г. а. 20) и 6-гональ-ная пирами да (6mm, п. г. а. 12), N = 9 — 7-гональная бипирамида (14m2, п. г. а. 28) и 8-гональная пирамида ( 8 mm, п. г. а. 16), N = 11 — 9-гональная бипирамида (18m2, п. г. а. 36) и 10-гональная пирамида (10mm, п. г. а. 20). Для N = 7 (34 кластера) и N = 9 (2606 кластеров) все H_v и H_e даны в статье (Войтеховский, 2022).

Возможно, уже здесь, в зародыше, отчасти содержится ответ на вопрос, почему кристалл прирастает не только отдельными атомами, но и группами. Эта гипотеза Д. Баларева^*** активно обсуждалась (Юшкин, 1971; Юшкин, Баларев, 1993; Асхабов, 2022). Высокая симметрия как критерий отбора и перескоки невозможных атомных конфигураций известны для фуллеренов С_n. У них n может быть только четным из-за особенностей геометрии (Kroto, 1987). Их рост возможен лишь присоединением пар атомов. При этом ст аб ильные ф ормы требуют высоких т. г. с. (C₆₀, C₈₀: 53m; C₇₀: 10m2…). Как показано выше, малые полиэдрические кластеры с нечетным числом атомов противоречат принципу равного ближайшего окружения. Но здесь мы должны остановить чисто геометрическое рассуждение, т. к. для больших кластеров следует учитывать виды атомов и особенности химических связей.

Рис. 2. Баларев Д., 1935 (архив Д. П. Григорьева) и обложка книги (Юшкин, Баларев, 1993)

Fig. 2. Balarev D., 1935 (D. P. Grigoriev’s archive) and the cover of the book (Yushkin, Balarev, 1993)

Протозародыш

Сферическая частица может быть с касанием окружена 12 такими же. А вот задача 13-го шара решалась несколько столетий, в том числе И. Кеплером и И. Ньютоном. Ряд доказательств приводит Ф. Тот (1958). Переход к кластеру из 13 частиц означает важный рубеж — он и все последующие могут быть допированы атомами, проскользнувшими внутрь оболочки. Появляются внутренние и наружные атомы. И это прекращает действие принципа равного ближайшего окружения в прежней форме.

На рис. 3 (слева) показана частица А, окруженная шестью такими же, задающими слой плотной шаровой упаковки. Добавление частиц снизу и сверху (по 3) в позициях В и/или С (рис. 3, справа) порождает множество периодических кристаллических, непериодических (ортогонально слоям) квазикристаллических и некристаллических структур. Возможность последних обеспечена тем, что 12 частиц первой координационной сферы могут довольно свободно скользить по поверхности частицы А (что и породило задачу 13-го шара), нарушая в растущем кластере кристаллографический порядок. Так, синтезированы оболочечные ико-саэдрические кластеры PdN c N = 13, 55, 147, 309, 561, 923…, в каждой оболочке 10n2 + 2 частиц, n — порядковый номер оболочки (Дубов и др., 1995).

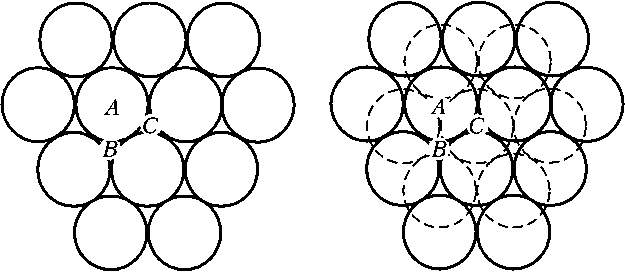
Рис. 3. Окружение шара А шестью другими и перспективы роста кластера

Fig. 3. Surrounding ball A with six others and the growth prospects of the cluster

В каком кластере может быть опознан будущий кристалл? Это вопрос, на который нет простого ответа. Если иметь в виду узнавание с помощью методов рентгеновской дифракции, то в кластере с несколькими сотнями или тысячами атомов, образующих плоские сетки. Если речь идет о кластере, в котором различим принцип, дающий шанс стать кристаллом, то с 13 атомами. В нем уже узнаваем фрагмент плотной шаровой упаковки.

Заключение

Как же возникает протозародыш кристалла, если «коротко и наглядно»? Он возникает в результате отбора самых симметричных полиэдрических атомных кластеров, устроенных по принципу равного ближайшего окружения; их рост состоит в присоединении пар атомов ради преодоления нечетных конфигураций. Фрагмент плотной шаровой упаковки, дающей шанс стать кристаллом, узнаваем в 13-атомном кластере.

Здесь судьбы кластеров расходятся. Принцип равного ближайшего окружения заработает снова для внутренних атомов больших кластеров, выбравших путь кристаллического роста. Это их структуры определят внешние формы согласно принципу: т. г. с. есть фактор-группа пространственной г. с. по подгруппе трансляций. До того он не работает, структуры и внешние формы флуктуирующих зародышей еще не определены и между собой не связаны.

Автор благодарит рецензентов за весьма профессиональные рекомендации.