Из опыта преподавания. XVII. Бордюры и предельные группы Кюри

Однажды во время лекции о кристаллографических бордюрах, т. е. линейных односторонних ритмично упорядоченных орнаментах (Шубников, 1940), нами было отмечено, что наши прабабушки, замыкая ритмические узоры на платьях, рубахах, фуражках и тюбетейках, всякий раз превращали трансляции в поворотные оси. Математический формализм позволяет замкнуть кристаллографический бордюр в «бесконечно удаленной точке» (это непросто представить), тем самым создав ось ∞ бесконечного порядка, ведь на бесконечном кольце умещается бесконечно много конечных (даже как угодно больших) повторяющихся фрагментов орнамента. Но каждый изучавший кристаллографию должен ощутить здесь некую опасность. С бесконечностями всегда так…

В кристаллографию ось ∞ ввел П. Кюри для описания физических сред, полей и свойств кристаллов. Идея родилась в пору его работы в минералогической лаборатории Сорбонны и открытия пьезоэлектричества в 1880 г. (Шпольский, 1956), но систематически изложена в статьях 1883–1884 гг., много раз переизданных (Curie, 1894, 1908; Кюри, 1966а, 1966б, 1966в).

С точки зрения симметрии бордюров и предельных групп Кюри по семь — замечательное совпадение! Но среди последних лишь пять с одной осью ∞, а две сферические к нашему случаю не относятся. Тогда где еще 2 группы? Или 2 бордюра при замыкании исчезают? Обсуждению этой коллизии и посвящена статья.

Иерархия бордюрови предельных групп Кюри

К иерархиям бордюров и групп Кюри сделаем несколько пояснений. В предложенных ранее обозначениях бордюров (Войтеховский, 2020, 2021) буквами обозначены (рис. 1, слева): продольная плоскость Р, поперечная П, центр инверсии С (эквивалентен ортогональной бордюру оси L2), трансляция Т и скользящее отражение Т* (композиция Т и отражения в Р на половине трансляции). Их полный перечень в символе упрощает сравнение бордюров. При этом Т вкладывается в Т*, а Т* — в РТ (рис. 1, справа).

Многие отдавали должное П. Кюри в связи с предельными группами симметрии, но большей частью ввиду их приложений к физическим объектам и явле-

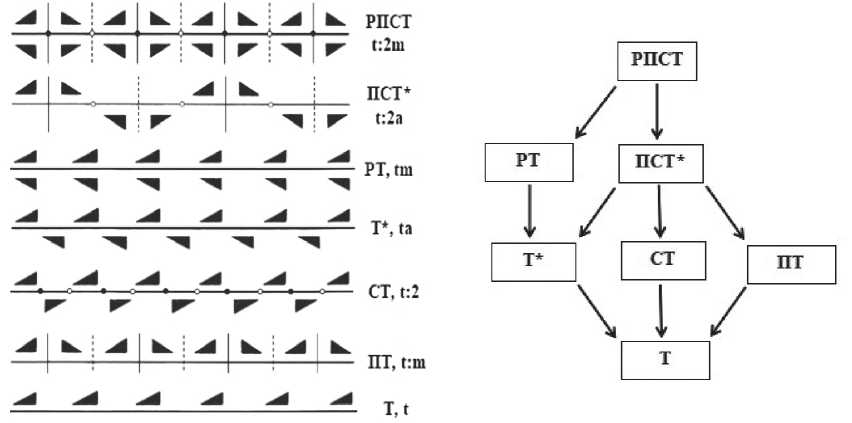
Рис. 1. Бордюры (слева) и их иерархия по группам симметрии (справа). Обозначения по: Войтеховский, 2020, 2021 и Шубников, 1940

Fig. 1. Borders (on the left) and their hierarchy by symmetry groups (on the right). Designations by: Voytekhovsky, 2020, 2021 and Shubnikov, 1940

ниям (Иоффе, 1956; Копцик, Рез, 1981), а также принципу диссимметрии (Шубников, 1961; Шафрановский, 1964, 1966; Chalmers, 1970; Ismael, 1997; Castellani, Ismael, 2016). Геометрический аспект с акцентом на симметрии конусов, цилиндров, сфер и их природных прототипов обсуждается кристаллографами (Шубников, 1956, с. 592; 1972, с. 34; Шафрановский, 1957). Вложения предельных групп обсуждаются редко, это весьма специфическая тема. И в монографии (Вайнштейн, 1979,

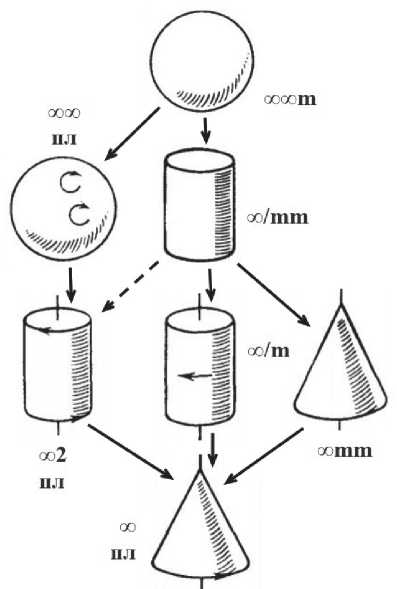
Рис. 2. Иерархия предельных групп симметрии Кюри (Вайнштейн, 1979). Буквы «пл» указывают на энантиоморфные (правые и левые) разновидности

Fig. 2. Hierarchy of limit symmetry groups of Curie (Weinstein, 1979). The letters «пл» indicate enantiomorphic (right and left) varieties с. 107) допущена неточность. Группа ∞2 вкладывается не только в ∞∞, но и в ∞/mm (рис. 2, дано штрихами). Кристаллографические примеры: (222 → 422) → 4/mmm, 32 → (6m21 → 6/mmm), 622 → 6/mmm. В скобках: в 1-м случае — подгруппы скрученного, во 2-м — покоящегося цилиндров. Студентам бывает трудно понять, как вращающиеся конусы и цилиндры вкладываются в неподвижные. Следует указывать, что последние допускают вращение в обе стороны.

Оси вращения конусов обычно показывают ориентированными (Вайнштейн, 1979, с. 100). Это лишнее, ведь конусы уже запрещают переворачивающие элементы симметрии, разрешая лишь продольные плоскости в группе ∞mm (рис. 2). Ориентировки осей нужны при замене конусов на цилиндры, что сделано далее при рисовании на них замкнутых бордюров. Обратная замена цилиндров на конусы, склеенные основаниями, применена в работе (Франк-Каменецкий и др., 1984, с. 19). В обозначениях предельных групп имеет место разброд. А. В. Шубников не экономил на указаниях взаимного расположения элементов симметрии: ∞ , ∞ · m , ∞:m , ∞:2 , m · ∞:m , ∞/∞ , ∞/∞ · m (Шубников, 1956, с. 592; 1972, с. 34). Позднее стали прибегать к сокращениям и/или модификациям символов (в т. ч. на рис. 2).

Группы симметрии замкнутых бордюров

На рис. 3 показаны замкнутые бордюры на цилиндрах с числом повторяющихся фрагментов n = 1–4. Перечислим порождаемые ими кристаллографические точечные группы симметрии (т. г. с., в скобках — для n = 6), найдем формулы симметрии для любого n и совершим переход n → ∞, понимая под ∞ как угодно большое n.

РПСТ: mm2, mmm, 6m2, 4/mmm, (6/mmm) …; 2nm2 (ложная инверсия — см. далее) для нечетных и n/mmm для четных n; переход: ∞/mm (нечетные n) и ∞/mmm 2 (четные n) — покоящийся цилиндр;

ПСТ*: 2/m , 4 2m , 3 m … ; n m (ложная инверсия) для нечетных и 2n 2m (истинная инверсия — см. далее) для четных n; переход: ∞ m (?);

РТ: m , 2/m , 6 , 4/m , ( 6/m ) …; 2n (ложная инверсия) для нечетных и n/m для четных n; переход: ∞/m — вращающийся цилиндр;

Т*: 1 , 4 , 3 … ; n (ложная инверсия) для нечетных и 2n (истинная инверсия) для четных n; переход: ∞ (?);

СТ: 2 , 222 , 32 , 422 , ( 622 ) …; n2 для нечетных и n22 для четных n; переход: ∞2 (нечетные n) и ∞22 ³ (четные n) — скрученный цилиндр;

ПТ: m , mm2 , 3m , 4mm , ( 6mm ) …; nm для нечетных и nmm для четных n; переход: ∞m (нечетные n) и ∞mm ⁴ (четные n) — покоящийся конус;

Т: 1 , 2 , 3 , 4 , ( 6 ) …; n ; переход: ∞ — вращающийся конус.

Пропавшие бордюры

Итак, пропавшими оказались замкнутые бордюры Т* и ПСТ* со скользящими отражениями, превратившимися в инверсии. (При этом инверсии С бордюров на рис. 1 превратились в оси 2 , перпендикулярные осям ∞ замкнутых бордюров на рис. 3.) Это им не нашлось эквивалентов в схеме предельных групп Кюри (рис. 2). И трудно сразу предложить геометрические формы и/или движения, промежуточные (по вложению) между вращающимися конусом и цилиндром для Т*, скрученным и обычным цилиндрами для ПСТ* (рис. 2 и 3).

К характеристике именно этих бордюров относятся инверсионные оси, названные выше ложными и истинными. Фраза «инверсионная ось n-го порядка» имеет смысл для любого n и подразумевает поворот фигуры на угол 360/n с последующим отражением в лежащей на оси точке, истинным центром инверсии не являющейся. Но легко увидеть и прочитать объяснение в учебниках кристаллографии для n = 1–4 и 6, что инверсионная ось нечетного порядка — композиция простой оси того же порядка и истинного центра инверсии: 2n+1 = L_2n+1 + C ( 1 = C, 3 = 3 + C); инверсионная ось четного порядка вида 4n+2 — композиция простой оси в два раза меньшего нечетного порядка и перпендикулярной плоскости 4n+2 = L_2n+1 + m ( 2 = 1 + m = m , 6 = 3 + m ). Те и другие — ложные. Лишь инверсионные оси четного порядка вида 4n истинные, т. е. не выражаемые через обычные элементы симметрии, известные до открытия О. Браве оси 4 на тетраэдре. Именно истинные инверсионные оси составляют специфику замкнутых бордюров Т* и ПСТ*. В схеме предельных групп Кюри (рис. 2) все оси ∞ обычные. Но куда могут быть вложены инверсионные оси ∞ ? Почти очевидно,

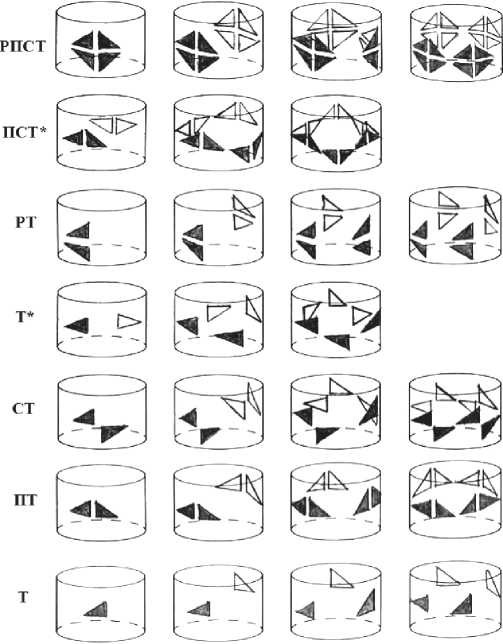
Рис. 3. Замкнутые бордюры. Пояснения в тексте

Fig. 3. Closed borders. See text что только в группы ∞/m вращающегося и ∞/mm покоящегося цилиндров.

В приведенном списке бордюров есть 27 кристаллографических т. г. с. (без 5 кубических). Это естественно, ведь среди порождающих операций симметрии — все разрешенные для конечных фигур. Но 4 т. г. с. получены дважды: 2 (Т, СТ), m (ПТ, РТ), mm2 (ПТ, РПСТ), 2/m (РТ, ПСТ*). Их элементы симметрии по-разному ориентированы относительно осей ∞ конуса и цилиндра. Так как n = 1, 2, 3, …, в приведенном списке содержатся вообще все (кроме кубических) т. г. с. По-видимому, их вывод через замкнутые бордюры никем ранее не выполнялся⁵.

Ось бесконечного порядка

Присмотримся к оси ∞. По аналогии с осями Ln конечных порядков следует полагать, что при повороте

на 360о фигура (в т. ч. бесконечная — среда или поле) совмещается с собой ∞ (бесконечно много) раз при повороте на бесконечно малый угол 360/∞. В этом рассуждении, тиражируемом в университетских курсах, не все гладко. Ведь ∞ — не число, его нельзя получить арифметически, потому и 360/∞ — не число. Оба сопротивляются представлению уже потому, что не рождают убедительную интуицию числа. Конусы, цилиндры и сферы у П. Кюри — символы гладкости. Суть не столько в этих формах, подобранных для иллюстрации, сколько в группах присущих им элементов симметрии, характеризующих известные физические (потенциально бесконечные и бесформенные) поля, среды и свойства.

Вот еще один способ понимания. «Конус подобен n-гональной пирамиде средних сингоний» (Шафра-новский, 1973). В той же мере цилиндр подобен n-гональной призме. При n → ∞ пирамиды и призмы (с оговорками, заставляющими грани дружно убывать по площади) стремятся к конусу и цилиндру, n-гранные фуллерены с икосаэдрической симметрией — к сфере. А вот похожее рассуждение. «Из дискретных элементов симметрии можно получить элементы непрерывной (предельной) симметрии групп Кюри. Из оси симметрии n-го порядка можно получить ось бесконечного порядка, устремляя n к бесконечности. Образом точки при таком преобразовании является окружность и поворот осуществляется на бесконечно малый угол. Второе непрерывное преобразование — это трансляция на бесконечно малое расстояние, получаемое из обычной конечной трансляции с помощью того же предельного перехода. Образом точки при таком преобразовании является прямая линия» (Франк-Каменецкий и др., 1984, с. 14). Впрочем, повод к такому представлению дал сам П. Кюри, обсуждая соотношение плоскостей «непрерывной» и «перемежающейся» симметрии (т. е. плоскости скользящего отражения) в бесконечных системах: «Мы имеем плоскость непрерывной трансляционной симметрии, если трансляция τ бесконечно мала» (Кюри, 1966б, с. 79).

Выражение «стремиться к бесконечности» туманно. Нельзя стремиться к чему-то столь плохо определенному, «что больше любого наперед заданного числа». Тогда почему нам кажется понятным символ 360/∞, обычно принимаемый за 0? Следует различать два нуля: один — арифметический, другой — неощутимый в его малости антипод необъятной огромности (Генон, 2013). Иначе говоря, есть два взаимно обратных стремления: n → ∞ и 360/n → 0. Но если мы легко перешагиваем исчезающе малый зазор между 360/n и 0, то перешагнуть неубывающую бездну между растущим n и ∞ нельзя⁶. Это выглядит парадоксом, но в смысле Г. Кантора (по числу точек) эти континуумы на числовой оси равномощны.

Наконец, неограниченно увеличивая порядок оси симметрии n, мы циклично переходим от нечетного числа к четному и наоборот, в этом смысле топчась на месте. Выше показано, что в этом кроется важный мо- мент — разные формулы симметрии для нечетных и четных n даже в одном типе замкнутого бордюра, и более того, рождение истинной инверсии при четных n, кратных 4.

Геометрическая интерпретация

На рис. 4 дана геометрическая интерпретация т. г. с. замкнутых бордюров, включающая известную схему предельных групп Кюри. Полосы, параллельные образующим цилиндра, двуцветные (условно «+» и «–») с краем и без края (сплошная и точечная линии соответственно). Еще лучше представлять «+» и «–» как черный и белый цвета. Тогда при n → ∞ полосы, становясь все тоньше, дадут системы прямых линий (образующих цилиндров), тем не менее сохраняющих их т. г. с. В прямоугольных рамках — соподчиненные бордюры, соответствующие предельным группам Кюри ∞/m вращающегося и ∞/mm покоящегося цилиндров (рис. 2).

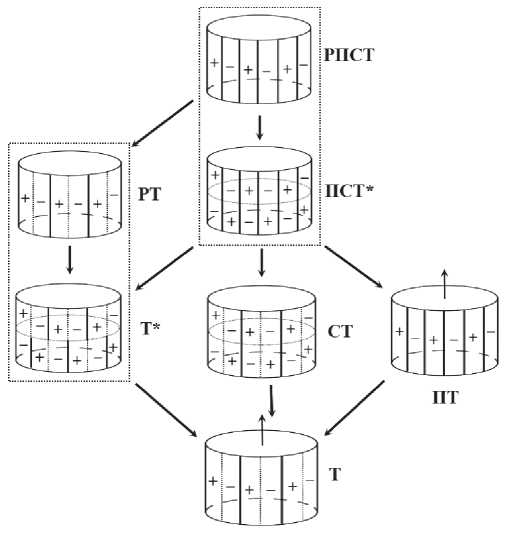
Рис. 4. Геометрическая интерпретация замкнутых бордюров. Пояснения в тексте

Fig. 4. Geometric interpretation of closed borders. See text

Заключение

Поясним еще раз, почему в системе Кюри оказалось 5, а не 7 предельных групп с одной «осью изотропии» ∞. В статье Кюри (1966а, с. 58) дана классификация из 10 «систем повторяемости», 3 из них — с осями ∞: сфера, цилиндр и «усеченный» (?) конус. Вращений не указано, но для конуса (и только для него) дан физический прототип — электрическое поле. В другой статье Кюри (1966б, с. 88) предложена более детальная классификация из 24 «конечных систем повторяемости и симметрии». В «сферическом» типе выделены вращающаяся7 и покоящаяся8 сферы, в типе «с двусто- ронней осью изотропии» — скрученный9 и покоящий-ся10 цилиндры, в типе «с осью изотропии и противоположной ей» — вращающийся цилиндр11, вращаю-щийся12 и покоящийся13 конусы.

В обеих работах для систем с осями конечных порядков рассмотрены варианты с нечетными и четными n, получены все 32 т. г. с. конечных фигур — без учета инверсионных осей последний результат не мог быть получен. Но, переходя к пределу при n → ∞ (суть именно в этом!), Кюри совместил их с обычными осями симметрии¹⁴. По нашему мнению, ось L_∞ = L_n при n → ∞ можно понимать в том смысле, что n как угодно велико, но сохраняет специфику (нечетное или четное, в последнем случае — кратно ли 4). В этой ситуации имеет место взаимно однозначное соответствие т. г. с. замкнутых бордюров и предельных групп Кюри, что логично. Мы не видим рациональности в игнорировании двух замкнутых бордюров с истинными инверсионными осями.

Исчерпана ли тема? Присмотримся к понятию гладкости. Столь осязаемое для сферы, цилиндра и конуса, оно скрывает математический омут. Гладкость функции характеризуется числом ее непрерывных производных (своего рода аналоги физической шероховатости). Чтобы быть гладкой, надо прежде быть непрерывной, хотя не обязательно равномерно непрерывной. Не углубляясь в нюансы определений, предположим, что уточнения этих понятий для полей, сред и свойств еще откроют путь к детализации предельных групп Кюри.

Возможное возражение состоит и в том, что ко всем предельным группам сам П. Кюри и последователи подобрали физические прототипы. Есть ли таковые для двух «инверсионных» замкнутых бордюров (предельных групп)? Мы пока затрудняемся их указать. Но возможность их геометрической интерпретации в единой системе с известными предельными группами (рис. 4) обнадеживает. Может быть, найдутся и физические прототипы, и тогда окажется, что известные предельные группы симметрии — лишь первое приближение к описанию реальности. «В заключение отметим, что идеи Пьера Кюри в области учения о симметрии нельзя считать до конца оформленными. Это сделают будущие поколения» (Шубников, 1956, с. 602).

Автор благодарит рецензентов за рекомендации, способствовавшие лучшему изложению результатов.