Избирательное повышение жёсткости - путь к эффективным конструкциям

Рассмотрим задачу об отыскании конструкции минимального объёма, которая в единственном случае нагружения имеет заданное обобщённое перемещение. Решение будем проводить пока без учёта условий прочности.

В направлении ограничиваемого перемещения приложим единичную обобщённую силу и по формуле Максвелла-Мора вычислим перемещение, предполагая, что конструкция разбита на m конечных элементов, работающих в плоском напряжённом состоянии

А = t f     dS„

'⁼' S E ⁵ ’             _                       _      (1)

[R * ] = [R (R - ^ R ) + R (R - ^ R ) + 2( 1 + a )R R J

L ’ J L x ’' X’ ' ’ y 1' y ’' y ’ ~’ x 1/       '       • ’ / xy’ xy’-l

Здесь R i = CT5 ’ - поток усилий в i-ом элементе от единичной нагрузки; R = ст5 ’ - поток усилий в i-ом элементе от расчётной нагрузки; 5 i -толщина элемента; S_i – площадь элемента в плане; E i , ^ i - модуль упругости и коэффициент Пуассона материала элемента.

Отметим одно важное обстоятельство. Здесь формула Максвелла-Мора используется не как классическое средство вычисления коэффициентов канонической системы уравнений для раскрытия статической неопределимости, а в своём чистом, изначальном смысле применительно к конструкциям любой степени статической неопределимости.

Единичная обобщённая сила и расчётная нагрузка - суть векторы правых частей в методе

конечных элементов и поэтому внутренние усилия R i и R i в элементах определяются обычной процедурой метода конечных элементов. Если используются конечные элементы с постоянным полем напряжений, то формула (1) упрощается

_А= m^ fR^Js, t l E’5’

•

Для тонкостенных конструкций объём материала запишется в виде:

m

V = t S i 5 i .              (3)

i = 1

Минимизируем этот объём при условии

А = А o ,                 (4)

где А o - заданное значение обобщённого перемещения.

Величины слагаемых в (2) показывают вклад каждого элемента в создание ограничиваемого перемещения. Если величина f R , ] большая, то перемещение во многом определяется деформациями i-го элемента и добавлением в него материала или переходом на более высокий модуль упругости можно существенно уменьшить суммарное перемещение. А если величина f R_f ] отрицательна? Поскольку единичная обобщённая сила приложена в направлении нежелательных деформаций, то отрицательное значение интеграла Мора, показывает, что в данном месте необходимо разрешить конструкции деформироваться как можно больше, то есть нужно уменьшить жёсткость элемента.

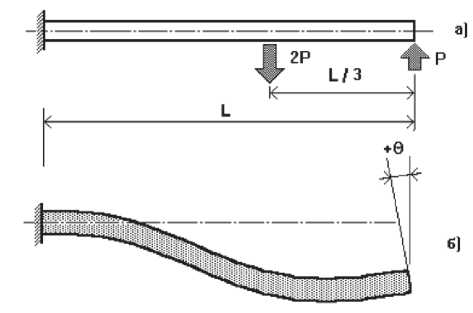
Рис. 1. Пример для иллюстрации способов достижения заданных деформаций

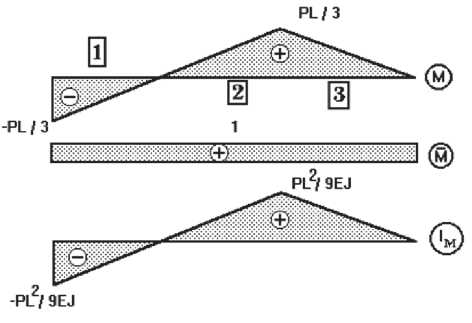
Рис. 2. Эпюры моментов и интегралов Мора

Для иллюстрации рассмотрим консольную балку, нагруженную двумя силами, как показано на рис.1а. Потребуем ограничить угол поворота концевого сечения, см. рис.1б.

Приложим на конце балки в направлении (+ 5 ) единичный изгибающий момент м = 1 и найдём распределение интегралов Мора, вычисляемых в данном случае как

тов, для которых интегралы Мора положительны; n – количество элементов, где интегралы Мора положительны.

Обозначим

IM

MM

=       dz.

^∫ L EJ

А+

Л

Тогда

[R i^* ] S i

E i 5 '

[Ri*] Si i Ei 5

Положим для простоты EJ = const и тогда перемножением эпюр моментов расчётного и единичного случаев нагружения получим распределение интегралов Мора по длине балки, см. рис. 2.

Из анализа эпюр рис. 2 видно, что уменьшение изгибной жёсткости 2 и 3 участков вызовет увеличение угла 5 , в то время как уменьшение жёсткости участка 1 приведёт к его уменьшению. Заданного значения угла поворота 5 концевого сечения можно добиться либо усилением зоны 23, либо ослаблением зоны 1, либо этими действи-

А = А+ -А .

ями одновременно.

Вообще, отрицательные значения интегралов Мора всегда безошибочно укажут такие зоны конструкции, которые необходимо ослабить для достижения желаемых перемещений. Из (2) видно, что в этих местах нужно назначать толщины, минимально допустимые по прочности, конструктивным или технологическим соображениям, или каким-либо другим условиям. Поэтому ограничение (4) перепишем следующим образом. В выражении (2) соберём все отрицательные слагаемые. Вынося минус за знак суммы, получим

n

А = I i=1

[R’^s, _- у [R * ]S , E i 5 . - . 1 E i s _t

Здесь: 5 - принятые минимально допустимые толщины элементов с о ~ трицательными значениями интегралов Мора; 5 - толщины элемен-

и условие (4) будет иметь вид

А+=А о + А-.           (10)

Поскольку в зонах с отрицательными интегралами Мора приняты минимально допустимые толщины, то толщины этих элементов исключим из числа проектных переменных и найдём оптимальное распределение материала только в зонах с положительными интегралами Мора. Таким образом, имеем задачу условной оптимизации: минимизировать объем материала конструкции

V~ = ^S, 5, ^min (11)

i = 1

при условии (10).

Решение найдём методом множителей Лагранжа. Составим функцию

n

∑ ~

Si 5 + Л (А -Ао -А ), (12)

i = 1

где Л 1 — множитель Лагранжа. Условия минимума функции имеют

^L = 1 - Л [R^] = 0 , i = 1 , 2 ,...n;   (13)

дЗ.        4 E 3.2     ,      ,

i ii

— = A+-A -A = 0.

дк °

Из уравнений (13) имеем

S i S i

V i

- °xi" P-Oyi - °yi" E°xi - 2( 1+ PiKyi o.-----— +o —+o -------- xi E yi E xyi E z                                                    z                                                          z

=[ ° xi ^£ Xi ^{+ o}, ^ yi ■ ^o .-'■'. ' c°^nst i=l,2,..n.

*

s. = к [Ri-]

i 1 _E

.

Подставляя (15) в (14) найдём жителя Лагранжа

значение мно-

_VS ^fR i ^J ^ i

.       [ i = 1 V ^E i

^A i = л----"AT

.

Уравнение (15) с учётом (16) запишется в виде

s

s- i=1

[Ri* ]

Ei

•

[Ri* ]

Ei

i = 1,2,...n. (17)

Выражение (17) определяет закон распреде-

ления материала по элементам конструкции, обеспечивающий заданное зна ч ение обобщённого перемещения при усилиях R i и R_i

При наличии зон с отрицательными интегралами Мора, то есть при A^- + 0 , мы имеем возможность получить проект с нулевым значением обобщённого перемещения: Д_o = 0. Другими словами, мы можем отыскать конструкцию, которая будет абсолютно жёсткой относительно ограничиваемого перемещения. Более того, возможно удовлетворение требования A o < 0, но при условии, что |A ₀1 <  A - , то есть можно добиться, чтобы конструкция деформировалась в сторону, противоположную своим реальным деформациям при первоначальном распределении материала. Если же участки с отрицательными интегралами Мора

отсутствуют, то мы можем только уменьшить существующее обобщённое перемещение.

Выражение (13), определяющее условие ми-

нимума объёма материала конструкции при ог-

раничении A o = A - перепишем следующим об-

разом:

Ш=1

Е S.2 к , ii 1

или

[R ] S 1

—i__i = — = c°nst, i = 1,2,...n. (20)

Et Si Vi   A

Подставляя в (2 ~ 0) значение [R i* ] учитывая, что R i = Siov , получим

из (1) и

Отсюда видно, что соотношение (13) определяет важное свойство построенного по (17) проекта, а именно: в оптимальной конструкции с заданным значением обобщённого перемещения, в зонах с положительными интегралами Мора удельная работа внутренних сил, возникающих от единичной нагрузки, на деформациях расчётного случая нагружения должна быть постоянна во всех элементах конструкции. В зонах с отрицательными интегралами Мора следует разрешить конструкции деформироваться как можно больше, для чего надлежит использовать в этих местах низкомодульные материалы с большими допускаемыми деформациями.

Требования статической аэроупругости, такие, например, как отсутствие дивергенции крыла, могут рассматриваться как ограничения на крутильные деформации. При использовании критериев оптимальности эти ограничения вводятся как неравенства и, в случае крыла, мерой жёсткости конструкции служат упругие перемещения некоторого количества выбранных, «характерных» или «типичных» сечений, расположенных по потоку. Деформации таких сечений и их аэродинамические характеристики для целей нашего исследования сводятся к анализу деформаций единственного характерного сечения. Обоснование применимости такого подхода и правило выбора характерного сечения для конкретного крыла выходит за рамки данной статьи и может быть найдено в работе [1].

В качестве примера рассмотрим проектирование конструкции крыла обратной стреловидности с ограничением на угол закручивания характерного сечения, расположенного на относительном расстоянии z = 0.81 от корня крыла. За прототип примем крыло с формой в плане как у самолёта «Беркут С-47», но выполненного из изотропного (не композиционного) материала, см. рис. 3.

Приложенная нагрузка имеет передний центр давления и соответствует полёту с максимальной перегрузкой. В процессе оптимизации нагрузка не корректировалась в соответствии с упругими свойствами крыла. Нам было важно показать принципиальную возможность получения конструкции, не подверженную дивергенции, а не решать точно аэроупругую задачу. В качестве начального распределения материала по силовым элементам было принято распределение, обеспечивающее избыточную жёсткость.

Деформации крыла с начальным распределени- миниевых сплавов, обладающих высоким ресур- ем материала показаны на рис. 4.

Результаты оптимизации показаны на рис. 5, 6, 7.

Видно, что задняя кромка перемещается больше передней, за счёт этого углы атаки (закручивания поточных сечений) уменьшаются и дивергенция полностью исключена.

Из сравнения рис. 6 и рис. 7 видно, что для обеспечения заданных деформаций в сторону уменьшения угла атаки необходимо усиливать конструкцию в передней части крыла (там, где интегралы Мора положительны) и ослаблять в задней части крыла. При этом увеличивается прогиб зад- сом и надёжностью.

Новый критерий оптимальности позволяет управлять деформациями конструкции на стадии проектирования и разрабатывать проекты, в которых распределение материала в одной её части управляет деформациями другой её части. Эффективность такого управления показывает распределение интегралов Мора.

Рассмотрим под этим углом конструкции живой природы. Крыло морской чайки, см. рис. 8, обладает как прямым участком, так и участками прямой и обратной стреловидности и, судя по тому, что птица не ломает крылья в полёте, не подвержено явлению дивергенции во всех полётных ситуациях.

ней кромки, что уменьшает угол атаки.

Мы добились этого результата при исполь-

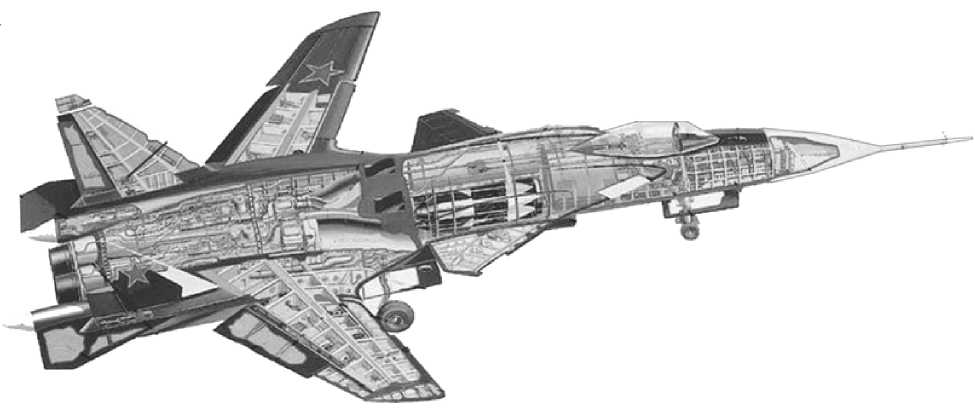
Рис. 3. Прототип крыла для оптимизации

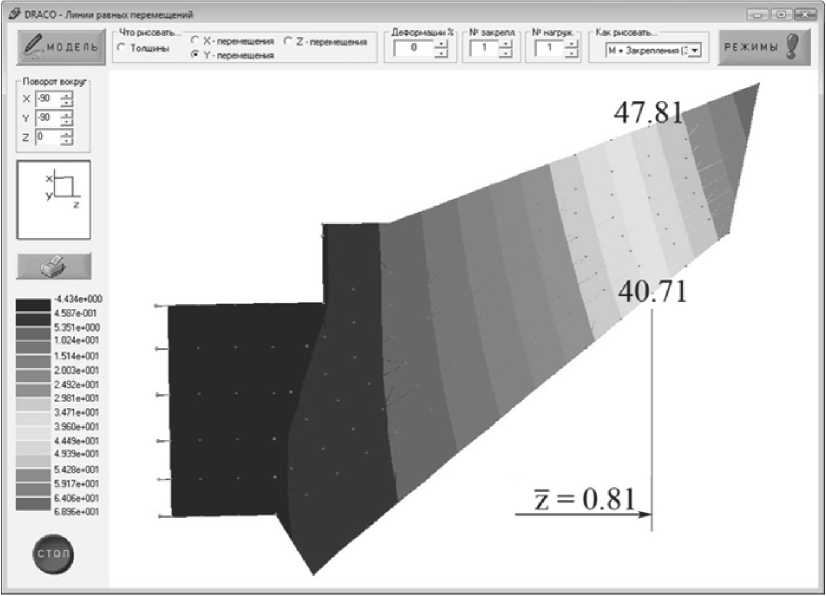
Рис. 4. Вертикальные перемещения сечений крыла до оптимизации

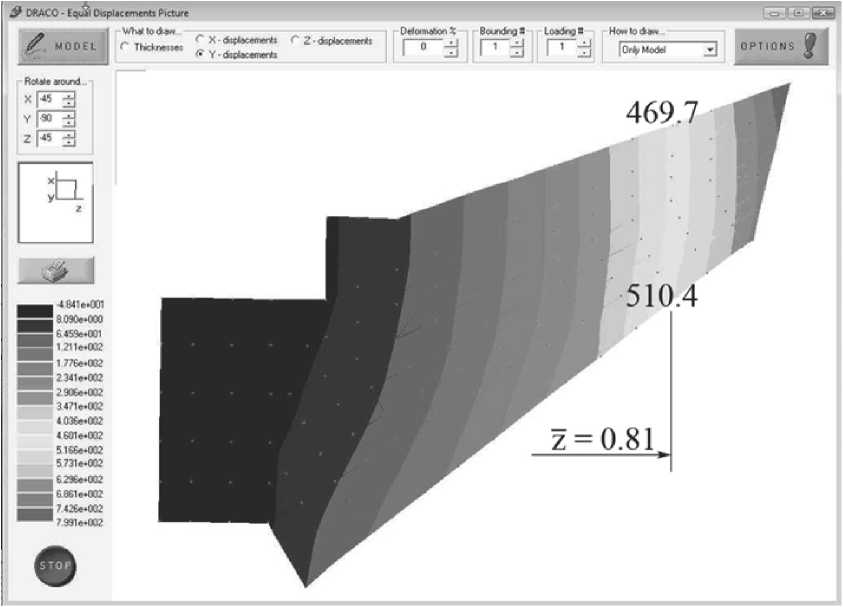
Рис. 5. Вертикальные перемещения сечений крыла после оптимизации.

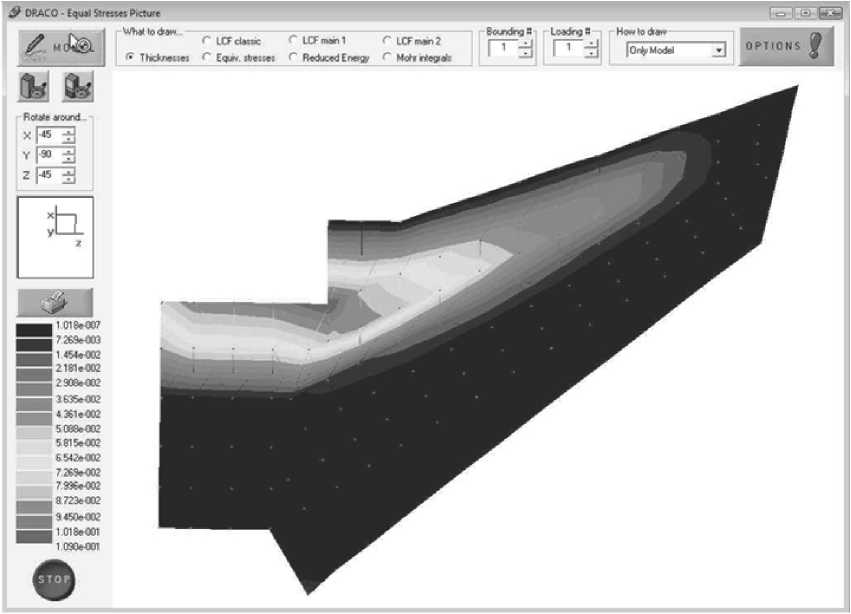
Рис. 6. Распределение толщины обшивки после оптимизации (тёмные участки – толщины минимальны)

Когда чайка парит, то крыло развёрнуто и приближается к форме прямого крыла с максимальным аэродинамическим качеством. Во время ловли рыбы чайка срывается в пикирование, значительно увеличивая скорость полёта. При этом она складывает крылья, придавая им стреловидную форму. Полёт во время пикирования полностью управляем по каналам тангажа, крена и рысканья, причём машущих движений, как правило, не происходит, и крылья остаются в стреловидном положении.

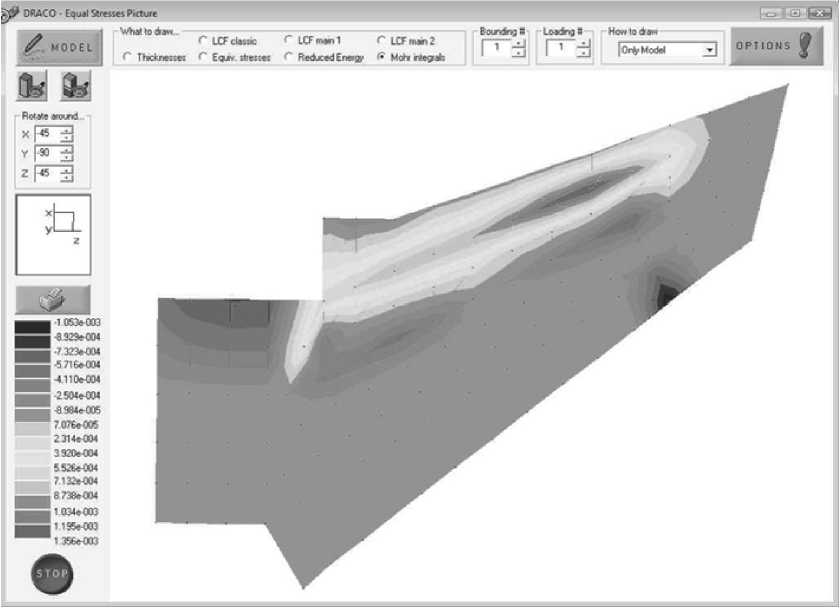
Рис. 7. Распределение интегралов Мора в обшивке после оптимизации (светлые участки – интегралы положительны)

Рис. 8. Крыло морской чайки

Природа поступила весьма мудро, соединив в одной конструкции прямую и обратную стреловидность. Изгиб консольной части крыла прямой стреловидности “нагружает” корневую часть обратной стреловидности крутильными деформациями в сторону уменьшения угла атаки. Поэтому часть крыла с обратной стреловидностью начинает работать уже имея запас отрицательного угла атаки, который уменьшается по абсолютной величине по мере приближения к “фюзеляжу”.

Проведём виртуальную модификацию самолёта Ан-140, как показано на рис. 9. Такая модификация позволит увеличить крейсерскую скорость за счёт снижения волнового сопротивления и сохранить высокие взлётно-посадочные

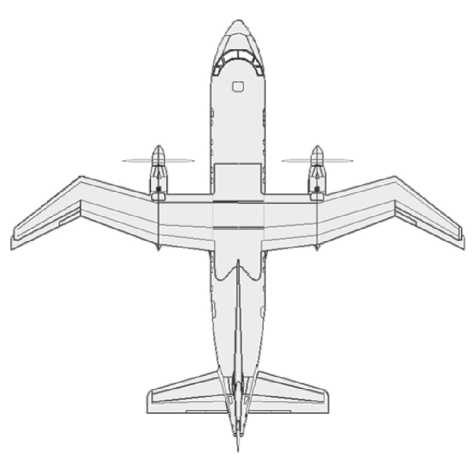
Рис. 9. Модификация крыла самолёта Ан-140 характеристики за счёт прямого участка и участка обратной стреловидности крыла.

Такое крыло имеет деформации, показанные на рис. 10. Видно, что углы упругого закручивания сечений равны нулю (прогибы сечений по передней и задней кромке равны).

Для данной модификации крыла мы не выполняли оптимизацию распределения материала. Представленные на рис. 10 упругие деформа-

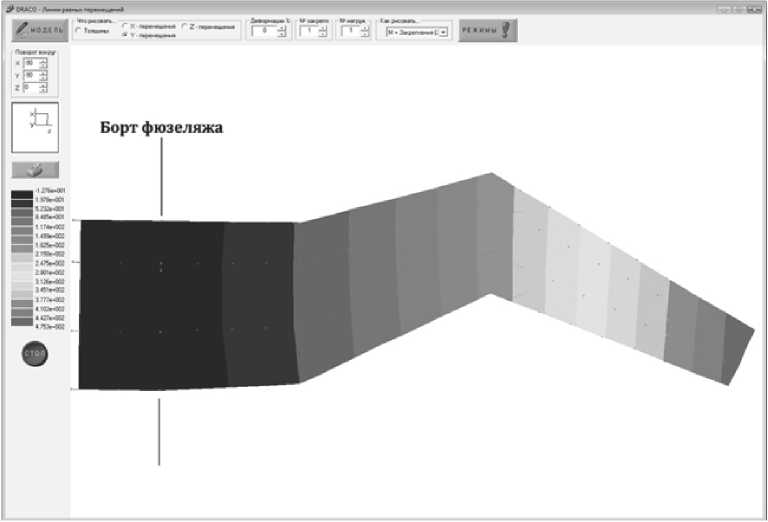
Рис. 10. Вертикальные прогибы точек крыла

ции соответствуют типичному распределению материала в кессонном крыле.

ВЫВОДЫ

Полученный новый критерий оптимальности позволяет проводить избирательное уменьшение деформаций не только за счёт добавления материала в элементы конструкции, но и за счёт снятия части материала с других элементов. Тем самым повышается эффективность получаемых проектов.