Изгиб композитного бруса

В настоящее время большое внимание уделяется всестороннему исследованию композитных материалов. Так, в [1] разработана многослойная броня – алюмооксидная керамика (тканый материал), армированная эпоксидной смолой и алюминиевым сплавом. В [2] исследованы колебания композитной балки из функционально-градиентного в двух направлениях материала, армированного углеродными нанотрубками. В работе [3] определена и сопоставлена эффективность различных схем облицовки пластины композитными покрытиями. В [4] исследована устойчивость подкрепленного отсека фюзеляжа самолета, выполненного из композиционного материала, при чистом изгибе и нагружении внутренним давлением. В [5] проведены исследования стойкости формируемого композитного материала при высокоскоростном соударении. В [6] приводится математическая постановка задачи о вынужденных установившихся и собственных колебаниях рассматриваемых смарт-систем, а также результаты численных расчетов, из которых следует, что графеновые композиты могут быть использованы для дополнительного демпфирования колебаний смарт-структур на основе пьезоэлементов. В работе [7] на основе метода конечных элементов разработан вычислительный алгоритм для решения ограниченного класса задач об изгибе композитных пластин, армированных системами однонаправленных высокопрочных волокон. Разработана модель динамического деформирования и разрушения композитных материалов, в которой учитывается нелинейность диаграмм ударного нагружения с упрочнением, зависящего от скорости деформирования [8].

В [9] Ю. Н. Работнов предложил модель композитного материала с упруго-пластическим связующим и упругими волокнами. При этом между волокнами и связующим, при нагружении, действует постоянное касательное напряжение. На основе этой модели в предлагаемой статье рассмотрено напряженное состояние бруса, изготовленного из композиционных материалов. Задача решена с помощью законов сохранения, построенных для системы дифференциальных уравнений, описывающих напряженное состояние бруса. Методику построения законов сохранения можно найти в [10; 11]. Законы сохранения позволяют эффективно решать краевые задачи для ряда уравнений механики деформируемого твердого тела. Примеры решения таких задач можно найти в [12–15].

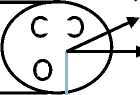
Рассмотрим брус, изготовленный из упруго пластического материала, армированный n упругими волокнами. Один конец бруса закреплен в точке z = 0 , на втором конце бруса при z = l подвешен груз весом Р в начале координат, который совпадает с центром тяжести сечения (рис. 1).

Матрица бруса имеет модуль упругости G и предел текучести при чистом сдвиге ks . Волокна расположены вдоль оси бруса в произвольном порядке параллельно оси z . Каждое волокно имеет круглое сечение, центр волокна располагается в точке с координатами (xi,yi) , радиус волокна равен R , модуль упругости Gi . Пределы текучести волокон превосходят предел текучести матрицы. Касательное напряжение между волокном и матрицей равно τ < ks .

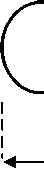
l

о о

P

о

x

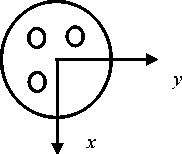
Рис. 1. Брус с волокнами с подвешенным грузом

Fig. 1. A fiber beam with a suspended load

Заданный процесс описывается уравнением равновесия и уравнениями совместности де- формаций [13]:

∂τ    ∂τyz    Px ∂2τ    ∂2τ         P ∂2τ xz                           xz xz                         yy

+    =-   ,      +     =-       ,       +=

∂x    ∂y      I    ∂x2    ∂y2     (1 + ν)I    ∂x2

σ _z

P ( l - z ) x I

I = ∫ x ² ds . S

Из двух последних уравнений (1), с учетом первого получаем

∂τ xz   ^∂τ yz      P ν

-

∂ y    ∂ x   I (1 + ν )

y - 2 K ,

где K – постоянная, являющаяся углом поворота объемного элемента бруса относительно оси

z ; τ _xz , τ _yz , σ _z – компоненты тензора напряжений; S – поперечное сечение бруса; I – момент инерции относительно оси y ; ν – коэффициент Пуассона.

Граничные условия на боковой поверхности бруса, свободной от напряжений и находящейся в пластическом состоянии, имеют вид

τ n +τ m =0, τ2 +τ2 =k2 =k2 -1/3σ2, xz yz               xz yz            s           z где n0 ,m0 – компоненты вектора нормали к боковой поверхности, которые можно записать в виде

τ _xz = m mk , τ _yz = ± nk .

На границе между волокном и матрицей выполняются условия

τxzmi - τyzni =τ, τx2z + τ2yz =k2, где ni ,mi – компоненты вектора нормали к боковой поверхности i-го волокна, которые запишем в виде

τ _xz = m_i τ ± n_i V k ² -τ ², τ _yz = n_i τ m m_i 7 k ² -τ ².                          (4)

Далее в формулах (3)–(4) выбирается верхний знак.

Для удобства дальнейших вычислений введем следующие обозначения: τ _xz = u , τ _yz = v .

Тогда задача (1)–(4) запишется так:

F₁ = u x — v_y + Px / 1 = 0, P v         „

F = u — v--у + 2 K = 0,

• ² y ^x (1 + v )

на боковой поверхности:

u = — mk, v = nk, на границе волокна и матрицы:

u = m i t + n i^ k ² — t ² , v = n i t — m i^ k ² — t ² .

Определение. Законом сохранения для системы уравнений (5) назовем выражение вида

A_x ( x , у , u , v ) + B y ( x , у , u , v ) = © F ₁ + w₂ F ₂,                          (6)

где ю ₁, ю ₂ - некоторые линейные операторы, одновременно не равные тождественно нулю.

Более подробно с техникой вычисления законов сохранения и их использования можно ознакомиться в [3–5].

Пусть

A = а ¹ u + Р ¹ v + у\ B = а ² u + р ² v + у ²,                           (7)

где а i , р ¹ , у ¹ - функции только от x , у .

Подставляя (7) в (6) получаем а x + а у = 0, р x + ру = 0, а = ©1, р = —су, а = су, р = ©1, yX + у У = —а1 Px /1 + р1[2 K — Pvу / (I (1 + v))].

Отсюда следует аX—ру = 0, px+аУ = 0, yx + у у = —а1 Px /1 + Р1[2 K — Pvу / (I (1 + v))].

Рассмотрим для системы уравнений (8) два решения, имеющие особенности в произвольной точке x ₀ , y ₀ сечения:

• ¹⁾    _а 1 = ^{x — x} 0          р 1 = _—        у ^— у 0

(x — x0)2 +(у — у 0)2’        (x — x 0)2 +(у — у 0)2’ у1 = 0, у2 =— Px arctg у у 0 +  Pv  (у — у 0 + (^0— + x — x0)arctg у у 0 +

I       x — x ₀    I (1 + v )            x — x ₀                x — x ₀

+ :2^{ln(( x — x} 0 ^{) 2} + ⁽ у ^— у 0 ^{) 2 ) —} K ^{ln(( x — x} 0 ^{) 2} + ⁽ у ^— у 0 ^{) 2 )} ,

• ²⁾    „1           у ^— у 0         o1           ^{x — x} 0

а* =          2             2 , p* =          22

^{( x — x} 0 ) + ^{( у — у} 0 )         ^{( x — x} 0 ) + ^{( у — у} 0 )

у* = 0,  у*2 = 2 Karctg у  у 0 — Pv [ у 0arctg у у 0 + x—x0 ln((x — x 0)2 + (у — у 0)2)] — x — x0 I (1 + v) x — x02

• ^— Px -^{ln(( x — x} 0 ^{) 2} + ⁽ у ^— у 0 ^{) 2 )} ,

где x ₀, y ₀ – постоянные.

Пусть ( x ₀, y ₀) – произвольная точка, принадлежащая связующему, и пусть в этой точке сохраняющийся ток имеет особенность вида (9) или (10). Тогда из (6) следует

JJ (Ax + By)dxdy = J Ady - Bdx-]T [J Ady - Bdx - J Ady - Bdx = 0,          (11)

S                        Г0                   i=1 Гi                   ε где ε окружность (x-x0)2 + (y- y0)2 = ε2 (рис. 2).

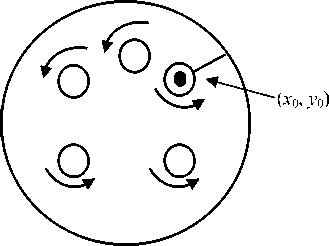
Рис. 2. Вычисление напряженного состояния в точке x ₀ , y ₀

Fig. 2. Calculation of the stress state at a point x ₀ , y ₀

Рассмотрим решение (9), полагая x - x ₀ = ε сos ϕ , y - y ₀ = ε sin ϕ , тогда из (11) с учетом (9), при ε → 0 , получаем

^{2 nT} x _Z ^{( x} 0 , y 0 ) = [J ⁽ m 0 ^k

Г0

x - x ₀

( x - x ₀)² + ( y - y ₀)²

- n ₀ k        ^{y - y 0}       ) dy

( x - x ₀)² + ( y - y ₀)²

-

- ( m ₀ k        ^y ₂ ^{- y 0}     ₂ + n ₀ k

( x - x ₀) + ( y - y ₀)

x - x ₀

( x - x ₀)² + ( y - y )²

+ у ) dx +

ⁿ ₍ ( m_i τ+ n_i k ² -τ ²)( x - x ₀) _- ( - n_i τ+ m_i k ² -τ ²)( y - y ₀)

i=1 Гi

( x - x ₀)² + ( y - y ₀)²

( x - x ₀)² + ( y - y ₀)²

) dy -

- (( m_i τ + n_i k ² - τ ² )

y - y ₀

( x - x ₀)² + ( y - y ₀)²

+

+ ( n_i τ + m_i k ² - τ ² )

x - x ₀

( x - x ₀)² + ( y - y )²

+ y 2 ) dx.

Рассмотрим другое решение уравнений (8) вида (9).

Почти дословно повторяя предыдущие рассуждения с решением (12), получаем

2 ^ПТ 23 ^{( x} 0 , y 0 ) = J ⁽ m 0 ^k

Г0

y - y ₀

( x - x ₀)² + ( y - y ₀)²

+ n ₀ k

x - x ₀

( x - x ₀)² + ( y - y ₀)

₂ ) dy -

- (-m0k

x- x0

(x-x0)2 +(y- y0)2

+ n0k

------yr^y0-----2 + Y» ))dx + (x-x0)2 +(y-y)2

n

+2 и (

i=1 Гi

( m_i τ + n_i k ²

-

( x - x ₀)² + ( y - y ₀)²

τ ²)( y - y ₀) ₊ ( - n_i τ + m_i

k - τ )( x - x ₀ )

( x - x ₀)² + ( y - y ₀)²

) dy -

- ( - ( m_i τ + n_i k ² -τ ²)

x - x ₀

( x - x ₀)² + ( y - y ₀)²

+ ( n_i τ+ m_i k ² -τ ²)

y - y ₀

( x - x ₀)² + ( y - y )²

+ y 2 ) dx.

Полученные формулы позволяют вычислить напряженное состояние в любой точке связующего материала. Те точки, где т Xz + T ^ z = k ² , будут находиться в пластическом состоянии, остальные точки среды, а также волокна, будут оставаться упругими. Предложенный метод решения позволяет построить упруго-пластическую границу в изгибаемом композитном брусе и тем самым оценить его несущую способность. Многообразие композитов [14 – 16] и их огромная практическая важность позволяют надеяться, что предложенная авторами методика позволит оценивать прочность конструкций изготовленных из композитов.

• 1.    Ахмед П. С., Абед М. С., Салим И. А. Экспериментальное исследование и численное моделирование баллистического воздействия на гибридный композит (оксид алюминия – тканый материал – эпоксидная смола – алюминий), используемый при изготовлении бронежилета // ПМТФ. 2023. № 4. C. 3–13.

• 2.    Пан М., Чжоу С. М., Ху Б. Л., Чзан Ю. Ц. Свободные колебания композитной балки из функционально-градиентного в двух направлениях материала, армированной углеродными нанотрубками // ПМТФ. 2023. № 5. C. 166–178.

• 3.    Кирпичников В. Ю., Кощеев А. П., Сятковский А. И. Экспериментальное исследование эффективности армированных вибропоглощающих покрытий // ПМТФ. 2022. № 1. C. 65–70.

• 4.    Железнов Л. П., Серьезнов А. Н. Исследование нелинейного деформирования и устойчивости композитной оболочки при чистом изгибе и внутреннем давлении // ПМТФ. 2022. № 2. C. 207–216.

• 5.    Голышев А. А., Долгова С. В. Влияние керамического волокна SiC в металломатричном композите на его стойкость при высокоскоростном нагружении // ПМТФ. 2022. № 6. C. 145–149.

• 6.    Матвеенко В. П., Ошмарин Д. А., Юрлова Н. А. Использование электропроводящих композиционных материалов для дополнительного демпфирования смарт-систем на основе пьезоэлементов // ПМТФ. 2021. № 5. C. 45–57.

• 7.    Петраков И. Е., Садовский В. М., Садовская О. В. Анализ изгиба композитных пластин с учетом различия сопротивлений растяжению и сжатию // ПМТФ. 2021. № 1. C. 172–183.

• 8.    Федоренко А. Н., Федулов Б. Н., Ломакин Е. В. Моделирование ударного воздействия на демпфирующие элементы, изготовленные из композитных материалов // ПМТФ. 2021. № 1. C. 100–107.

• 9.    Работнов Ю. Н. Механика деформируемого твердого тела. Москва : Наука, 1979. 743 с.

• 10.    Vinogradov A. M. Local symmetries and conservation laws // Acta Appl. Math. 1984. No. 2. P. 21–78.

• 11.    Senashov S. I., Vinogradov A. M. Symmetries and conservation laws of 2-dimensional ideal plasticity // Proc. Edinburg Math. Soc. 1988. No. 31. P. 415–439.

• 12.    Senashov S. I., Savostyanova I. L. Using conservation laws to solve boundary value problems of the Moisila-Teodorescu system // J. Appl. Industr. Math. 2022. Vol. 25, No. 2.P. 101–109.

• 13.    Gomonova O. V., Senashov S. I. Determining elastic and plastic deformation regions in a problem of unixaxial tension of a plate weakened by holes // J. Appl. Mech. Tech. Phys. 2021. Vol. 62, No. 1, P. 157–163.

• 14.    Senashov S. I., Savostyanova I. L., Cherepanova O. N. Elastoplastic bending of the console with transverse force // J. of the Siberian Federal University. Math. and Phys. 2019. Vol. 12, No. 5, P. 637–643.

• 15.    Сенашов С. И., Савостьянова И. Л. Об упругом кручении вокруг трех осей // Сибирский журнал индустриальной математики. 2021. Т. 24, № 1. С. 120–125.

• 16.    Новацкий В. Теория упругости. М. : Мир, 1975. 872 с.

• 17.    Милейко С. Т. Антони Келли и композиты сегодня. Ч. 2. Композиты с металлической матрицей // Композиты и наноструктуры. 2021. В. 1, № 3–4 (51–52). С. 59–107.

• 18.    Милейко С. Т. Композиты и наноструктуры // Композиты и наноструктуры. 2009. Вып. 1. C. 6– 37.

• 19.    Келли А. Инженерный триумф углеводородов // Композиты и наноструктуры. 2009. Вып. 1. C. 38–49.

• 1.    Ahmed P. S., Abed M. S., Salim I. A. [Experimental investigation and numerical modeling of ballistic effects on a hybrid composite (aluminum oxide – woven material – epoxy resin – aluminum) used in the manufacture of body armor]. PMTF . 2023, No. 4, P. 3–13 (In Russ.).

• 2.    Pan M., Zhou S. M., Hu B. L., Chzan Yu. Ts. [Free vibrations of a composite beam made of a functionally gradient in two directions material reinforced with carbon nanotubes]. PMTF . 2023, No. 5, P. 166–178 (In Russ.).

• 3.    Kirpichnikov V. Yu., Kosheev A. P., Syatkovsky A. I. [Experimental study of the effectiveness of reinforced vibration-absorbing coatings]. PMTF . 2022, No. 1, P. 65–70 (In Russ.).

• 4.    Zheleznov L. P., Serebrinov A. N. [Investigation of nonlinear deformation and stability of a composite shell under pure bending and internal pressure]. PMTF . 2022, No. 2, P. 207–216 (In Russ.).

• 5.    Golyshev A. A., Dolgova S. V. [The influence of SiC ceramic fiber in a metal matrix composite on its resistance under high-speed loading]. PMTF . 2022, No. 6, P. 145–149 (In Russ.).

• 6.    Matveenko V. P., Oshmarin D. A., Yurlova N. A. [The use of electrically conductive composite materials for additional damping of smart systems based on piezoelectric elements]. PMTF . 2021, No. 5, P. 45–57 (In Russ.).

• 7.    Petrakov I. E., Sadovsky V. M., Sadovskaya O. V. [Bending analysis of composite plates with taking into account the differences in tensile and compressive resistances]. PMTF . 2021, No. 1, P. 172–183 (In Russ.).

• 8.    Fedorenko A. N., Fedulov B. N., Lomakin E. V. [Modeling of impact on damping elements made of composite materials]. PMTF . 2021, No. 1, P. 100–107 (In Russ.).

• 9.    Rabotnov Y. N. Mekhanika deformiruemogo tverdogo tela [Mechanics of a deformable solid]. Moscow, Nauka Publ., 1979, 743 p.

• 10.    Vinogradov A. M. Local symmetries and conservation laws. Acta Appl. Math . 1984, No. 2, P. 21–78.

• 11.    Senashov S. I., Vinogradov A. M. Symmetries and conservation laws of 2-dimensional ideal plasticity. Proc. Edinburg Math. Soc . 1988, No. 31, P. 415–439.

• 12.    Senashov S. I., Savostyanova I. L. Using conservation laws to solve boundary value problems of the Moisila-Teodorescu system. J. Appl. Industr. Math . 2022, Vol. 25, No. 2, P. 101–109.

• 13.    Gomonova O. V., Senashov S. I. Determining elastic and plastic deformation regions in a problem of unixaxial tension of a plate weakened by holes. J. Appl. Mech. Tech. Phys . 2021, Vol. 62, No. 1, P. 157–163.

• 14.    Senashov S. I., Savostyanova I. L., Cherepanova O. N. Elastoplastic bending of the console with transverse force. J. of the Siberian Federal University. Math. and Phys . 2019, Vol. 12, No. 5, P. 637–643.

• 15.    Senashov S. I., Savostyanova I. L. [On elastic torsion around three axes]. Siberian Journal of Industrial Mathematics . 2021, Vol. 24, No. 1, P. 120–125 (In Russ.).

• 16.    Novatsky V. Teoriya uprugosti [Theory of elasticity]. Moscow, Mir Publ., 1975, 872 p.

• 17.    Mileyko S.T. [Anthony Kelly and composites today. Part 2: composites with a metal matrix]. Kompozity i nanostruktury . 2021, Vol. 1, No. 3–4 (51–52), P. 59–107 (In Russ.).

• 18.    Mileyko S. T. [Composites and nanostructures]. Kompozity i nanostruktury . 2009, Vol. 1, P. 6–37 (In Russ.).

• 19.    Kelly A. [Engineering triumph of hydrocarbons]. Kompozity i nanostruktury . 2009, Vol. 1, P. 38–49 (In Russ.).