Изгиб упругой консоли в поле центробежных сил: пороговые значения нагрузок

Задачи, связанные с изгибом консоли в поле центробежных сил, актуальны при разработке конструкций лопастей вертолетов, лопаток турбин и других конструкций, в том числе и применяемых в космосе, где присутствуют гибкие элементы консольного типа, находящиеся одновременно под действием растягивающей и сжимающей нагрузок.

Ранее задачи изгиба для консоли с сосредоточенной на конце массой в плоскости вращения и в плоскости, перпендикулярной плоскости вращения, рассматривались в работе [1], где при условии малости прогибов на основе решения линейных уравнений получена зависимость эффективного коэффициента жесткости от приведенной растягивающей нагрузки. Решение в геометрически нелинейной постановке применительно к расчету изгиба консоли в механизме центробежного регулятора скорости вращения вала дано в работе [2], где точные выражения для стрелы прогиба были определены через три эллиптических параметра Попова - эллиптический модуль и два значения эллиптических амплитуд на концах консоли. Изгибно-крутильные пространственные колебания стержня с учетом кориолисовых сил инерции при условии малости прогиба рассмотрены в работе [3].

Стремительное усложнение конструкций и исполнительных механизмов, основанных на геометрически нелинейном изгибе составных элементов, применение современных конструкционных материалов, а также ограничения, накладываемые условиями эксплуатации, приводят к необходимости исследования устойчивости нагруженной конструкции. Цель данной работы - дать аналитический метод расчета гибких элементов консольного типа при пространственном изгибе в поле центробежных сил.

Для практического применения можно выделить два вида нагружения консоли в поле центробежных сил, приводящих к двум различным вариантам изгиба.

Первый вариант - нелинейный изгиб в плоскости, перпендикулярной плоскости вращения. Он рассмотрен в работе [4], где получены точные аналитические решения, зависящие от одного параметра.

Второй вариант - нелинейный изгиб в плоско сти вращения, обусловленный растягивающей центробежной и изгибающей следящей нагрузкой, направленной перпендикулярно свободному концу консоли, ранее не рассматривался. Однако этот вариант в определенном приближе- нии моделирует, например, изгиб лопасти в плоско сти вращения, если набегающий на нее поток перпендикулярен ее оси.

Изучение статически равновесных форм изгиба консоли в поле центробежных сил после потери устойчивости, а также пороговых значений нагрузок; является актуальным и в связи с различными механическими и биомеханическими задачами требует дополнительного рассмотрения. Исследуем обозначенные выше варианты нагружения консоли и определим условия существования равновесных форм изгиба с точками перегиба и без них, а также значения пороговых нагрузок, при которых возможно существование таких статически равновесных форм.

Схемы нагружения консоли. Уравнения изгиба стержней хорошо известны. Наиболее подробно теория изгиба гибких стержней изложена в монографии [2]. В данной статье теорию изгиба стержней рассмотрим для случая больших геометрических нелинейностей, в основном следуя работам [1; 2; 5].

Введем систему координат Пусть x , у - декартовы координаты в плоскости изгиба стержня; l - криволинейное расстояние от начала координат вдоль линии стержня до рассматриваемой точки; 9 = 9 ( l ) - угол наклона касательной в текущей точке к линии стержня; d 9 / dl -кривизна этой кривой. Покажем возможные схемы нагружения консоли при вращении, а также необходимые для дальнейших выкладок обозначения действующих сил и характеристик упругой кривой (рис. 1).

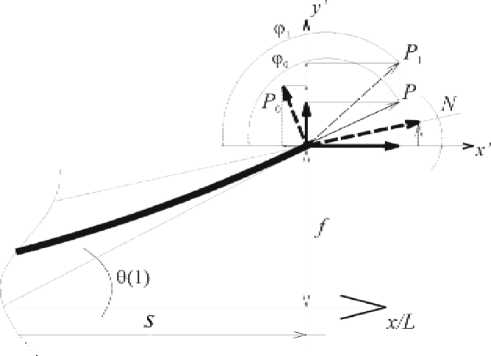
Рис. 1. Схемы нагружения консоли

Схема нагружения, показанная сплошными линиями, определяет изгиб в плоскости, перпендикулярной плоскости вращения. Пунктирными линиями отмечен изгиб в плоскости вращения. Через ф ₀, ф 1 обозначены углы приложения результирующих сил P и P ₁ в системе координат х ', у '; P 0 , N - соответственно сжимающая и растягивающая компоненты результирующих нагрузок; f – прогиб конца консоли; a - угол отклонения растягивающей составляющей N ; 9 - угол между осью Ох и касательной к оси стержня в случае, если за положительный отсчет углов выбрано направление против часовой стрелки. Заметим, что составляющая P ₀ в случае изгиба в плоскости вращения сохраняет постоянный угол с касательной, проведенной к концу консоли, т. е. является следящей.

В случае изгиба в плоскости, перпендикулярной плоскости вращения, проекция результирующей силы P_{x 2} совпадает с растягивающей силой N и имеет неизменное направление. В случае изгиба в плоскости чертежа растягивающая сила N поворачивается, и линия ее действия проходит через начальное сечение консоли.

Общий случай постановки задачи. Опишем решение задачи изгиба стержня, основываясь на работах [5; 6]. Пусть тонкий стержень, изначально прямой, закрепленный на левом конце и свободный либо закрепленный на правом, подвергается действию (сжатию под произвольным углом) внешней нагрузки, сосредоточенной на правом конце стержня. Изначальное неизогнутое положение стержня – вдоль оси Ox . Левый закрепленный конец стержня расположен в начале координат. Изгиб происходит с выпучиванием вверх.

Уравнение равновесия стержня приведем к уравнению нелинейного маятника:

d ²9 _ . . _

EI — p -P, sin 9 + P cos 9 = 0.

dl ^{2 xy}

Для упрощения уравнения введем угол наклона ф ₀ направления сосредоточенной силы Р к оси Ox . Для изучения возможных вариантов изгиба стержня рассмотрим угол направления силы ф изменяющийся в пределах от 0 до п /2. Величины P и ф ₀ считаются известными. В результате получим

P x = — P cos Ф ₀, P y = P sin Ф ₀.            (2)

Подставим выражения (2) в уравнение (1):

d 2 9 P • (a An ⁺   sin (^ ) = 0.

dl EI

Введем безразмерную длину t = l / L , изменяющуюся в пределах от 0 до 1 (здесь L – длина консоли), и сделаем замену у = 9 + ф ₀. Введем обозначение для собственного числа q ² = PL ²/ EI , где Е – модуль Юнга; I – момент инерции стержня, и получим уравнение для угла у типа уравнения нелинейного маятника:

d y + q ² sin у = 0.                ⁽³⁾

Решение этого уравнения хорошо известно из [2; 5]:

Y(t) = 2arcsin[k sn(qt + F1, k)], dy(t) / dt = 2kq cn(qt + F1, k), где функции sn и cn – эллиптические синус и косинус Якоби. Модуль эллиптических функций k и параметр F1

играют роль констант интегрирования, и их связь с действующей силой Р и углом приложения ф ₀ определяется по граничным условиям каждого конкретного случая изгиба стержня.

Поставим граничные условия к уравнению равновесия (1). Защемление на левом конце стержня требует, чтобы

9 (0) = 0.

На свободном конце должно выполняться условие равенства нулю момента сил:

d 9 ( L ) / dl = 0.

Для уравнения (3) эти условия запишутся в виде

Y (0) = ф ₀, d у (1) / dt = 0.                (4)

Уравнение равновесия стержня будет соответствовать (1), причем угол, под которым действует сила, в системе координат изменяется в пределах от 0 до п . В работах [5; 6] рассматривалось изменение этого угла в пределах от 0 до п /2. Угол, равный р, соответствует ситуации, когда стержень совпадает с осью Оx и деформация чистого изгиба исключена в связи с отсутствием перерезывающей составляющей нагрузки. Также исключено растяжение консоли, поскольку эта возможность в сформулированной модели не учитывается. Произвольность перемещения силы достигается за счет изменения компонент результирующей силы, что возможно при вращении консоли за счет увеличения растягивающей нагрузки при увеличении угловой скорости вращения.

В общем случае угол приложения результирующей силы в зависимости от результирующих проекций, когда за положительное направление при определении проекций выбрано направление вдоль консоли как ось Ox, можно представить в виде ф1 = пm - arctg(Py2 /Px2), m = 0,1,2, ... .      (5)

Пороговые значения нагрузок при изгибе в плоскости, перпендикулярной плоскости вращения. В случае изгиба в плоскости, перпендикулярной плоскости вращения, ф0 = п/2 + arctg(Px 2 /P 2 ), (6)

где Py2 , Px2 – соответственно поперечная и продольная составляющие результирующей нагрузки, были получены пороговые значения нагрузки для случая изгиба кон- соли перпендикулярно плоскости вращения:

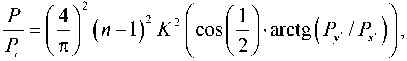
где Р = (п/2)2EI/L2 - эйлерова критическая сила; n - номер моды решения; K(k) – полный эллиптический интег- рал первого рода, откуда

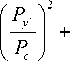
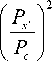
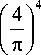
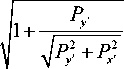
( n - 1)⁴ K ⁴ х

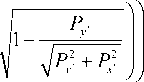
Соотношение (7) определяет конфигурации для действующих сил, при которых реализуются статически равновесные формы изгиба консоли при различном количестве точек перегиба, определяемых числом n. Зависи- мость поперечной нагрузки от растягивающей нагрузки [4] в соответствии с выражением (7) характеризует формы изгиба консоли с двумя и тремя точками перегиба (рис. 2). Однако в работе [4] анализ показанных зависимостей не проводился.

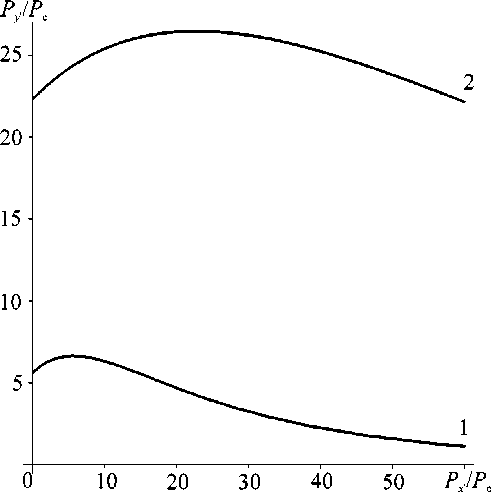
Рис. 2. Возможные значения пороговых нагрузок в соответствии с (2) для случая 1 (две точки перегиба) и 2 (три точки перегиба)

точками перегиба. Формы равновесия с двумя точками перегиба при некоторых значениях растягивающей составляющей нагрузки, когда конфигурация попадает в зону под максимумом, могут оказаться неустойчивыми и возможно, что через прощелкивание форма с двумя точками перегиба изменится в форму с одной точкой перегиба. В полученных решениях факт возможной неустойчивости определяется отсутствием решений для статической задачи. Реальный физический процесс перехода от формы с бомльшим числом точек перегиба к формам с меньшим числом точек неясен, однако теоретически соотношение (7) показывает условия (необходимые нагрузки), от которых зависит этот переход. Также не исключается возможность обратного перехода от форм с меньшим числом точек к формам с бомльшим числом точек, причем соотношение (2) позволяет выбрать оптимальные условия для реализации такого перехода. Например, при большой растягивающей нагрузке (кривая 1 рис. 2) необходима незначительная поперечная, возможно, им-пульсно приложенная нагрузка.

Изгиб в плоскости вращения. В данном случае необходимо ввести угол между направлением действующей силы N и осью Ox' , который позволит вычислить продольную растягивающую компоненту силы и добавку к заданной поперечной компоненте. Это возможно при постоянной угловой скорости вращения консоли.

Если обозначить угол между вектором N и осью Ox' через а , то выражения для компонент продольной и поперечной составляющих будут представлены выражениями

Рассмотрим рис. 2 более подробно. Анализ этого рисунка показывает, что равновесные формы изогнутой консоли, соответствующие определенному числу точек перегиба, возможны только при определенных значениях поперечной и растягивающей продольной нагрузок. Представленные зависимости также характеризуются тем, что при некоторых поперечных нагрузках переход от формы с одной точкой перегиба к форме с двумя точками перегиба возможен при двух значениях растягивающей составляющей: при фиксированной ненулевой растягивающей или поперечной составляющей нагрузки пороговое значение искомой другой составляющей нагрузки дается выражением (7); в случае отсутствия растягивающей нагрузки пороги для поперечной нагрузки принимают известные значения [5].

Обращает на себя внимание тот факт, что кривые для пороговых нагрузок имеют максимум, и поэтому при фиксированном значении поперечной нагрузки P могут быть два значения растягивающей нагрузки P x , , при которых возможны переходы от одной формы изгиба к другой.

Отметим, что конфигурации нагрузок, соответствующие форме изгиба без точки перегиба, могут быть любыми. Для формы с одной точкой перегиба возможны только те конфигурации, которые располагаются на кривой 1 и выше, для двух точек перегиба – на кривой 2 и выше. Таким образом, если мы выбираем конфигурацию сил для формы с одной точкой перегиба выше кривой 1 , то возможны равновесные формы и для формы изгиба с одной точкой перегиба, и для формы с двумя

P_x , = N cos а - P 0 sin 0 (1),

P y , = P ₀ cos 0 (1) + N sin a .              (8)

Угол а определяется стрелой прогиба и проекцией 5 длины стержня на ось Ox ':

a = v п + arctg

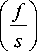
Если крайняя точка свободного конца консоли при изгибе находится в первом квадранте, то v = 0, если во втором квадранте, то v = 1.

Входящие в (9) величины f и s определяются следую-

щими выражениями:

f . у (1) =

L

2 k cn F ₁

( pK ( k ) - F 1 )

cos ф 1 +

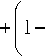
2[ pE ( k ) - E (am F , k )]) .

---------------------------- sin Ф,,

( pK ( k ) - F )    J

x (1)

5 =---

L

2 k cn F ₁

( pK ( k ) - F )

sin Ф 1

-

(   2[ pE ( k ) - E (am F , k )])

- 1--1----- cos ф,

I       ( pK ( k ) - F )    ^{J 41}

где p = 1, 2, 3, …, Е (am u , k ) – неполный эллиптический интеграл второго рода от эллиптической амплитуды Якоби.

Учитывая выражение для угла в случае изгиба в плоскости вращения ф 1 = п m - arctg( P y /P_x) m = 0, 1, 2, _, а также полученные в работе [6] соотношения для нагрузки, получим систему уравнений для определения угла ф 1

и эллиптического модуля k в зависимости от заданных нагрузок. В этом случае угол направления действия результирующей силы Ф 1 дается выражением

P y P„ cos 9 (1) + N sin a tg Ф 1 = — =------ ,

Px, P0sin 9(1)- N cos a или после тригонометрических преобразований

- P₀ cos( 9 (1) + Ф 1 ) = N sin( a + Ф 1 ).

Учитывая выражение для угла наклона касательной на конце стержня 9 (1) = - ф 1 + 2 arcsin( k ) [6], окончательно получим

N sin(ф₁ + a) + P ₀(1 - 2 k ²) = 0.         (12)

При отсутствии растягивающей силы N = 0. Тогда мы имеем известное предельное значение эллиптического модуля k ² = ¹ , соответствующее случаю изгиба следя-2

щей нагрузкой, направленной под прямым углом к оси консоли [7].

Используя выражения для проекций нагрузок (8), выражение для спектра собственных значений, полученное в [6], а также соотношение (12), запишем систему уравнений для определения эллиптического модуля k и угла приложения результирующей нагрузки ф 1 :

N sin(ф₁ +a) + P ₀(1 - 2 k ²) = 0,

‘4- 7 P ■ P -| - I [(2 n -1) K ( k )- F ] 2 = 0. (13) _ P_c              k п J

При заданных нагрузках N и P ₀, решая численным методом систему уравнений (13), получим значения искомых параметров, которые позволяют однозначно определить профиль изогнутой консоли.

Пороговые значения нагрузок. Последовательно рассмотрим пороговые ситуации для случаев первой и последующих мод.

Учитывая разложения для разностей эллиптических интегралов [8] в окрестности произвольной точки, переходя k ^ k0, а также учитывая, что 7 1 - k02 = |соз(ф1/2)| = cos(ф1/2) при -п < ф1 < п, получим выражения для угла a в случае перегибных форм изгиба. Для формы консоли с одной точкой перегиба n = 1 выражения (10) и (11) примут вид f = 2k0 71 - k02 cos Ф1 + [1 - 2(1 - k02)] sin Ф1 = 0, s = 2k0^1 - k2 sin Ф1 - [1 - 2(1 - k02)]cos Ф1 = 1. (14)

Тогда, подставив результат (14) в (9) и зная, что крайняя точка свободного конца консоли находится в первом квадранте (v = 0), имеем a = 0.                     (15)

Преобразуем систему (13) с учетом результата (15) при k ^ k 0 и для первой моды получим

P 7 N² + P = 0.

Этот результат в отсутствии растягивающей составляющей N = 0 соответствует известному для изгиба консоли следящей силой P ₀ случаю формы с одной точкой перегиба [7]. Также отметим, что потеря устойчивости формы происходит беспороговым образом.

Для последующих форм изгиба при n = 2, 3, учитывая, что крайняя точка свободного конца консоли при при- ближении к пороговому значению находится во втором квадранте (v = 1), получим a = п - Ф1.

Переходя к пределу k ^ k 0 с учетом соотношений (13), выведем выражение для пороговых нагрузок:

P>

^^COSф1 = 0, ф1 = ±2, 1(-N + Po) =f41 (n-1)2K2(sin(ф1/2)).

. Pc

Первоначально знак угла ф ₁ определяется для каждого порогового значения в зависимости от начального выбора направления деформирования. Например, в рассматриваемом случае при переходе от формы с одной точкой перегиба к форме с двумя точками перегиба Ф 1 = - п /2 (а также при любых других переходах) должно выполняться условие 9 (1) = 0, что означает смену знака эллиптического модуля при переходе от одной перегиб-ной формы к другой. Тогда в выражении (16) при извлечении квадратного корня выбирается положительный знак. Окончательно имеем

• ²                                I 1

PL = 1 4 I ( n - 1)² K ² м± + N .        (17)

P c 1п)           k 2 I P c

В отсутствии растягивающей составляющей нагрузки N = 0 выражение для пороговых нагрузок (17) соответствует известному выражению для случая изгиба консоли сосредоточенной следящей силой, приложенной к свободному концу под прямым углом [4; 6; 7]. Для того чтобы получить плавный переход между формами изгиба в условиях действия дополнительной растягивающей нагрузки, нужно увеличить пороговое значение следящей сжимающей нагрузки на величину добавляемой растягивающей нагрузки. А для того чтобы плавно вернуться от формы с бомльшим числом точек перегиба к форме с меньшим числом точек перегиба, достаточно увеличить растягивающую составляющую нагрузки. Таким образом, при заданной следящей нагрузке выше пороговой существует возможность мягкого перехода от формы изгиба с большим числом точек перегиба к форме с меньшим числом таких точек. При вращении увеличение растягивающей составляющей возможно при увеличении угловой скорости вращения. Таким образом, подбирая угловую скорость вращения, можно исключить переходы изгибающейся в плоскости вращения консоли к перегибным формам изгиба и тем самым управлять устойчивостью консоли.

При фиксированной ненулевой растягивающей или поперечной составляющей нагрузки пороговое значение искомой составляющей нагрузки определяется выражением (17). Отметим, что с увеличением растягивающей нагрузки увеличение порогового значения поперечной нагрузки происходит линейным образом в отличие от случая, рассмотренного в [7].

Точки перегиба. Выражения, определяющее перемещение точек перегиба и сжатия при изменении действующих на консоль нагрузок, следуют из (8) при значениях угла ц₁ и модуля k , определяемых по (13):

_ (2 m + 1) K ( k ) - F₂

• ¹    = (2 n - 1) K ( k ) - F ₂ , где F ₂ = F (sin( ф ₁ /2)/ k ).

Таким образом, на примере двух задач изгиба консоли в поле центробежных сил как частных случаев приложения действующих нагрузок можно сделать вывод о том, что если к консоли приложены несколько нагрузок, одна из которых следящая, то при некоторых значениях следящей составляющей переходы к новым перегибным формам консоли осуществляются плавно. Иными словами, при пороговых значениях следящей нагрузки, которые определяются всеми оставшимися составляющими, переход к перегибным формам, соответствующим последующей моде, является продолжением уже имеющейся формы в отличие от случаев, когда результирующая действующая сила носит поступательный характер. Также нужно отметить, что при наличии в системе действующих сил хотя бы одной следящей составляющей можно получить плавный переход исходной формы в перегиб-ную форму. При этом результирующая нагрузка и угол, под которым она направлена, будут соответствовать случаю изгиба вследствие действия поступательной нагрузки, направленной под произвольным углом к исходной форме изгиба.