Излучение из торца планарного диэлектрического волновода

На примере задачи излучения поля из торца плоскопараллельной диэлектрической пластины изложены строгий метод решения задач о рассеянии волн на резких неоднородностях волноводов [1, 2] и получение результатов численного расчета с любой наперед заданной точностью. Имеется ряд работ, в которых задача также ставится строго, однако численные решения получаются приближенными. Так, в работе [3] решение задачи сводится к системе бесконечного числа линейных алгебраических уравнений и предлагается приближенный метод ее решения методом редукций. В работе [4] строятся зависимости коэффициента отражения от параметров инжекционного лазера с двойной гетероструктурой. Используется вариационный метод решения. Из отраженных мод рассматриваются только первые две исходя из соображения, что доля остальных мод составляет менее 0,5 %. В [5] рассматривается отражение от торца диэлектрического лазера. Задача, учитывающая все типы волн, сводится к приближенному решению интегральных уравнений первого рода методом Ритца–Галеркина. В работах [6] и [7] строго поставленная задача для поля на торце волновода в виде интегрального уравнения первого рода решается приближенным итерационным способом.

• II.    Торец волновода

В настоящей работе рассматривается излучение из торца одномодового (TE-волна) симметричного волновода толщиной 2b (рис. 1). Поле собственной волны, распространяющейся вдоль оси z, с учетом временной зависимости exp (i ω t) запишем в виде

E x (y,z) = ^(y) exp(i(wt т Yz))-

Ниже используются выражения для функции поперечного сечения направляемых волн ф(у) и волн непрерывного спектра ф(к,у), введенных в работе [1]. Запишем функции для волн непрерывного спектра в виде pW

v ⁽⁰⁾ (к) cos к(у — b) + w ⁽⁰⁾ (к) sin к , у — b), y > b, cos K i y,                              — b < y < b,

v ⁽⁰⁾ (к) cos K(y + b) — w ⁽⁰⁾ (к) sin K(y + b), y <  — b,

VW

v ⁽¹⁾ (x) cos x(y — b) + w ⁽¹⁾ (x) sin x(y — b), cos xy, ^{— b} v ⁽¹⁾ (x) cos x(y + b) — w ⁽¹⁾ (x) sin x(y + b),

y>< b, y<

b,

- b,

где

N ⁽⁰⁾ (к) = Y(к) ² п[v ⁽⁰⁾ (к) + w ⁽⁰⁾ (к)],

v ⁽⁰⁾ (—) = cos — - b, w ⁽⁰⁾ (—) = —- sin — - b, κ

v ⁽¹⁾ (x) = cos xb, w ⁽¹⁾ (x) = sin xb,

— ₁ = (k ² (e ₁ — e) + — ² ) 2 , Y(—) = (k ² E — — ² ) 2 ,

N ^(-) (x) записывается аналогично, k = ш/с, с — скорость света, e и e - — относительные диэлектрические проницаемости внешней среды и волновода, κ, χ — поперечные волновые числа со стороны волновода и со стороны открытого пространства соответственно. Верхние индексы (0) и (1) у функций поля и постоянных распространения относятся к их значениям слева и справа от торца (z = 0) соответственно.

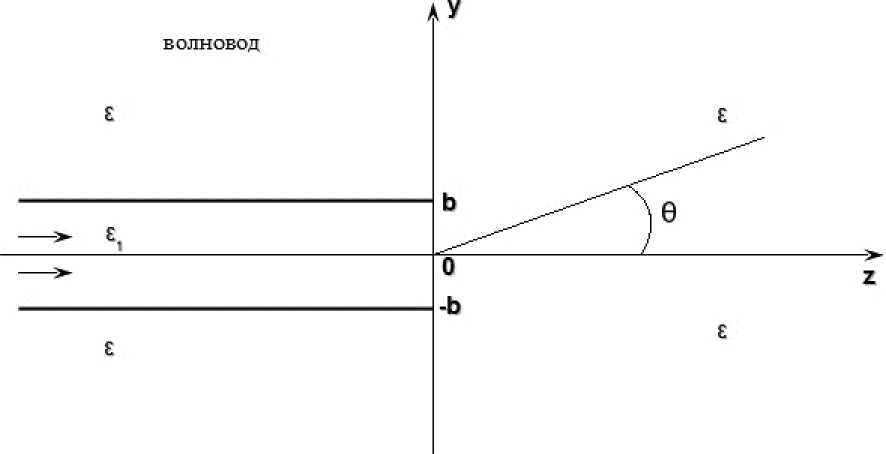
Рис. 1. Торец одномодового планарного волновода

Система собственных функций поперечного сечения имеет свойство ортогональности, которое может быть записано в виде

∞

Y i j ^iW-y = 1,

-∞

∞

Y i (x) j Wx,yN(x,y)dy = ^(x — x),                             (1)

-∞

∞ j ^1 (yN(x,y)dy = 0.

-∞

Поле на торце при z = 0 можно представить в виде суперпозиции собственных волн волновода [1] и свободного пространства в виде

∞ еХо)(у,О) = (A10) — B(0)N(0)(y) — j B(0)(—N(0)(—,y)d—,

∞ eX-) (у,0) = j A(1)(x)^(1)(x,y)dx, где A-0), B(0), A(1)(x), B(0)(—) — амплитуды падающей и отраженной направляемых волн и прямых и встречных волн непрерывного спектра соответственно.

Далее необходимо удовлетворить условиям непрерывности для тангенциальных компонент поля в плоскости стыка [1] в виде

E X ⁰⁾ (y,0) = E X ¹⁾ (y,0),

Н У ⁰⁾ (у,0) = Н У 1) (у,0).                                           (2)

Применяя к уравнениям (2) условия ортогональности (1), устраняем зависимость от поперечной координаты y и, с помощью ряда стандартных преобразований, получаем систему интегральных уравнений второго рода (подробнее см. [1]). Полученную систему решаем методом итераций. В качестве нулевого приближения были использованы значения амплитуд отраженных волн, равные нулю. Оценка точности приближений проводилась, как в [1] и [2], по балансу мощностей падающей и рассеянных стыком волн, то есть проверялось, что сумма мощностей отраженной направляемой, излученной влево и вправо от торца волн, равна мощности падающей на торец волны, принятой за единицу.

AP = 1 - B 1 ⁰⁾² - P a - P b .                             (3)

• III.    Результаты расчетов

В расчетах диэлектрическая проницаемость внешней среды принималась равной единице. Были рассмотрены три разные толщины волновода при двух значениях диэлектрической проницаемости волноведущего слоя. Параметры волновода соответствовали условиям одномодовости. В табл. 1 представлены результаты расчетов для квадратов коэффициента отражения на первом ,, (0)2 „(0)2

B 1 (1) и втором B 1 (2) шагах итераций, значения мощностей излучения в открытое пространство вправо на нулевом и первых двух шагах ( P a (0 , 1 , 2) ) и влево для первого шага P b (1) . Также указаны величины расхождения баланса мощностей A P для первого шага итераций. Обозначения соответствуют [1, 2]. Из табл. 1 видно, что при малой диэлектрической проницаемости волновода (е = 2,5) учет отражения вносит небольшую поправку в долю излученной мощности: 1-2%, в зависимости от величины 2b/A. Однако уже при е = 5 поправка второго шага итерации достигает 6-11%. Визуально величину поправок на разных шагах итераций можно видеть на диаграммах излучения (рис. 2 и 3).

Таблица 1

Результаты расчетов для нулевого и первых двух шагов итераций

ε	2b/A	R (0)2 B 1    (1)	R (0)2 B 1    (2)	P A (0)	P A (1)	P A (2)	P B (1)	A P
5	0,1	0.06537	0.07230	0.92133	0.78407	0.86397	0.00111	0.14943
	0,14	0.09220	0.10631	0.91065	0.70768	0.81847	0.00099	0.19910
	0,16	0.10232	0.11980	0.91371	0.68367	0.80529	0.00092	0.21307
2,5	0,1	0.00644	0.00652	0.98813	0.97488	0.98003	0.00099	0.01768
	0,14	0.01507	0.01546	0.97992	0.94894	0.96240	0.00104	0.03492
	0,16	0.01991	0.02053	0.97707	0.93634	0.95332	0.00102	0.04270

Данные получены по соотношениям

A ⁽¹⁾ (0) = ( — a ⁽¹⁾ (k sin(y))

для правого полупространства z >  0, и

B ⁽⁰⁾ (0) = ( — B ⁽⁰⁾ (k sin(0))

для левого. В левом полупространстве диаграммы графически неразрешимы из-за малости величин. Доля отраженной мощности указана в табл. 1. На диаграммах изображены результаты нулевого, первого и второго приближения. Было получено также несколько значений третьего приближения для проверки сходимости решения к точному. Они графически неразличимы и не представлены на диаграммах. Каждое последующее приближение дает существенно меньшую поправку, что является косвенным признаком сходимости к точному решению. Видно, что при толщинах волновода, близких к критической толщине второй моды, возрастают погрешности результатов для нулевого приближения.

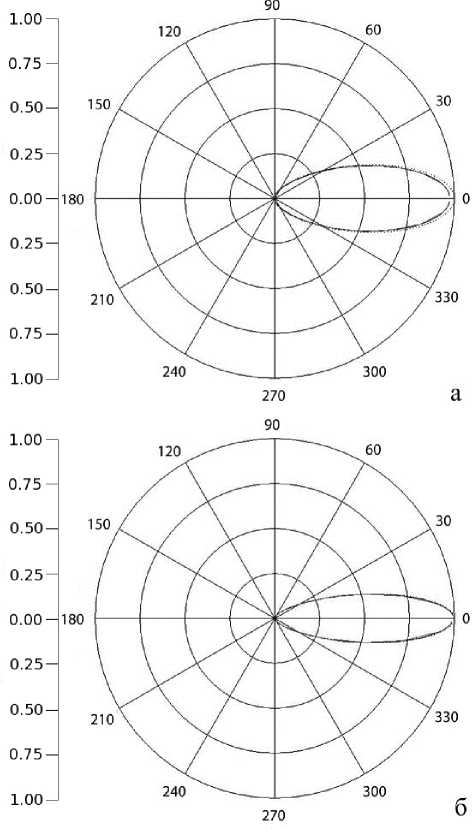
Рис. 2. Диаграммы излучения по мощности при е₁ = 2 , 5 , 2 b/X = 0 , 1 (а); 0 , 14 (б). Пунктиром обозначено нулевое приближение, сплошной линией — второе, штриховой — третье

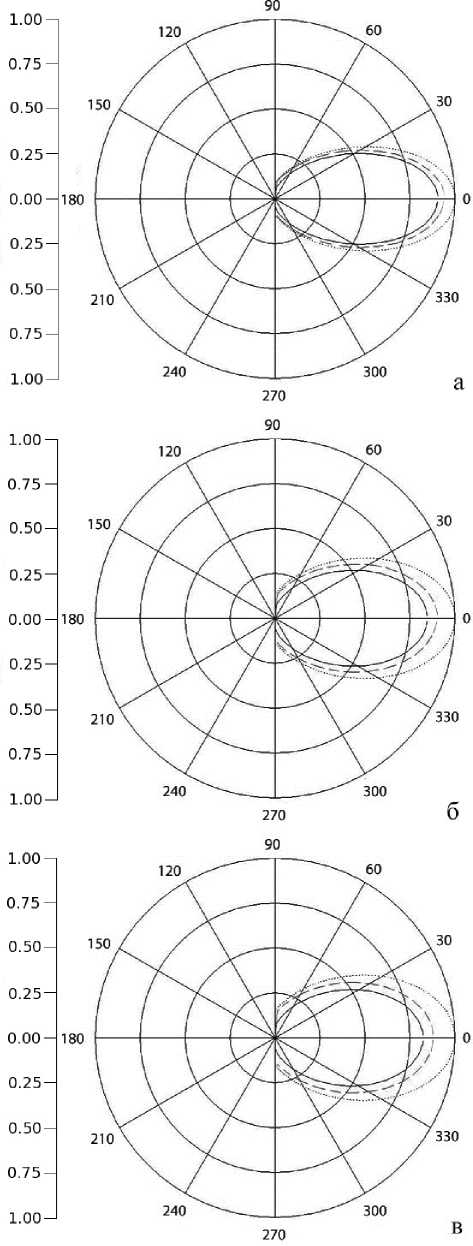
Рис. 3. Диаграммы излучения по мощности при е1 = 5 , 2 b/X = 0 , 1 (а); 0 , 14 (б); 0 , 16 (в). Пунктиром обозначено нулевое приближение, сплошной линией — второе, штриховой — третье

Сравнение двух способов расчета. В данной статье ставилась и решалась задача о непосредственном излучении поля в открытое пространство, а приведенные здесь результаты автор также получил из решения задачи о стыке двух волноводов, рассмотренной в работе [1], задавая:

• 1)    значение толщины второго волновода, равной 0;

• 2)    значение диэлектрической проницаемости второго волновода — 1.

Сравнение этих способов расчета показало, что способ, представленный в данной статье, дает более быструю сходимость решения и требует значительно меньших вычислительных ресурсов.

Автор выражает благодарность профессору В.В. Шевченко, под руководством которого выполнена данная работа.