Излучение ультразвука в расплавы легкоплавких металлов

Величина удельного импеданса и типоразмера излучателя определяет мощность и интенсивность ультразвуковых колебаний, излучаемых в жидкости, в том числе и в легкоплавких металлах.

Как известно, в случае колебаний с равномерно распределенной на поверхности излучателя нормальной скоростью - □, механический импеданс излучения определяется выражением [1]:

f P a d^

(1),

где р_а - давление, которое в силу реакции со стороны жидкости действует на площадку величиной- ds .

Средний удельный импеданс излучения, отнесенный к единице площади - S имеет вид [1]:

Za=^ = ra+JXa ,    (2)

где г_а и х_а активная и реактивная составляющие импеданса соответственно. Полная мощность ультразвука, излучаемого в жидкость при площади излучателя – S [1]:

N a = ^V>                            (3)

при соотношении d » Л, где X длина волны, активная составляющая импеданса принимается равной волновому сопротивлению жидкости.

Удельный импеданс для тонкого круглого диска диаметром – d= 2a, колеблющегося в бесконечном экране, согласно определению Релея имеет вид [2]:

'                           <4> где ρ – плотность, с – скорость звука, ρc – волновое сопротивление среды, а- радиус диска, k = -л - волновое число, ]1 - функция Бесселя

Л первого рода, первого порядка, К1 - модифицированная функция Бесселя, определенная Релеем [3]:

К(х) =-(--^ + ^г-

--)

¹⁴⁷ л X 3     5    3²-5²-7

Зависимости импеданса - z_a от величины - ka для дисков и пластин, колеблющихся, как поршень были получены в работах Л.Я Гутина. (например [3]) и Кикучи с сотрудниками [1,4]. Эти аналитические выражения имеют громоздкий вид и поэтому в рамках данной статьи они приведены из работы [4] в наглядном графическом виде [1]. При значениях ka <1 реактивная составляющая больше активной х_а >  г_а , как у диска с двухсторонним излучением, колеблющегося без экрана, так и диска, излучающего одной стороной в свободной пространство, с фиксированной противоположной стороной. Активная составляющая растет и становится преобладающей при ka =2, а при значении ka =3, реактивная составляющая падает до величины х_а « 0,2г_а. [1,4]. Важно, что для всех трех видов диафрагм при ka =2 и ka =3 значения г_а равны между собой с точностью графического изображения (рис. 1a,b). Кроме того эти значения близки для круглой и равновеликой прямоугольной пластины в бесконечном экране, а также для бесконечной пластины в бесконечном экране [4].

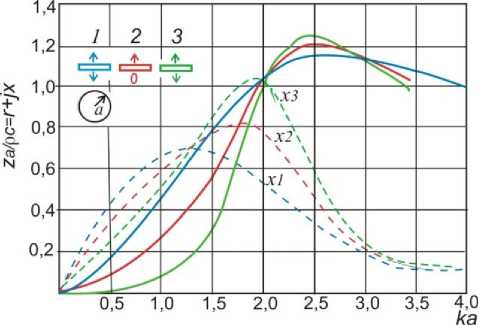
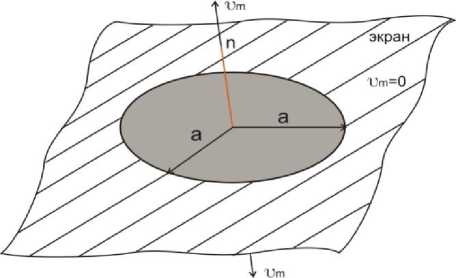
Рис. 1a,b Зависимости составляющих удельного импеданса z _a от ka [4]. Сплошные кривые - т_а, штриховые и штрихпунктирные кривые - х_а . а) 1 -диск в бесконечном экране с излучением двумя сторонами, 2 – c односторонним излучением и фиксированной другой стороной, 3 – диск, колеблющийся без экрана в свободном пространстве;

Принимая эти значения как критические, используем их для оценок мощности и интенсивности ультразвука (3), излучаемого в жидкие легкоплавкие металлы при значении ka =2 .

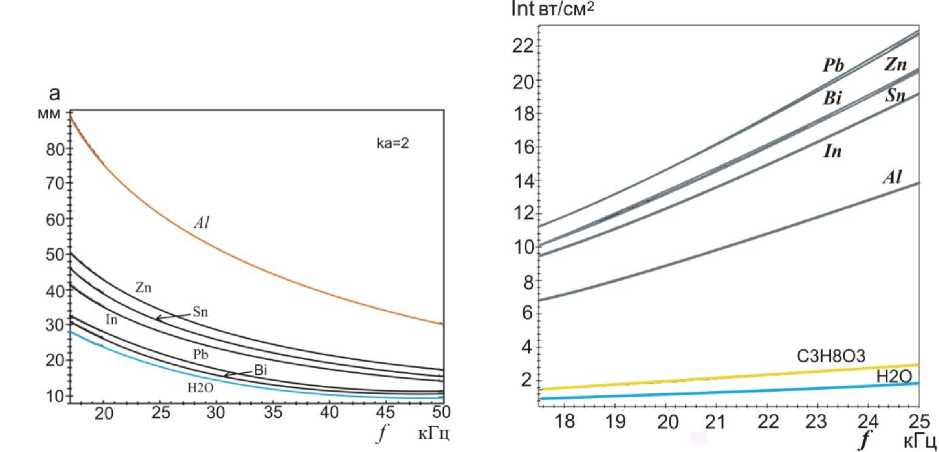
Рис. 2 a,b. a) Зависимости радиуса излучателя – a и интенсивности – Int от частоты– f в диапазоне низкочастотного ультразвука при значении ka =2.

На низких частотах (ка « 1) для диска в бесконечном экране с двухсторонним излучением, величина г_а определяется квадратом частоты - ш², а для диска, колеблющемся в свободном пространстве с двухсторонним излучением - ш ⁴ [1,4].

Мощность излучаемого ультразвука в соответствии с выражением (3) в этих случаях незначительна, и для получения оптимального значения ka = 2, радиус излучателя должен увеличиваться с уменьшением частоты (рис.

2а). Величина z_a=r_a +j'x_a пропорциональна волновому сопротивлению - p_tC (табл. 1), поэтому мощность и интенсивность (4) при равной величине ka =2 для случая расплавов металлов на порядок выше, чем в воде (рис 2b),. Таблица 1

Свойства легкоплавких металлов и воды [6-11]

Ме	Al	Ga	Zn	Sn	Cd	In	Pb	Bi	H 2 O
с; м/с	4750	2740	2700	2450	2215	2215	1760	1660	1483
p l cf10-7 кг/м2 сек	1,12	1,67	1,87	1,68	1,56	1,61	1,85	1,67	0,148
р; кг / м3 □	2369	6095	6920	6830	7790	7260	10510	10030	1000
o v 10-3Н/м2	520	720	785	526	564	340	442	376	73

Волновое сопротивление в таблице обозначено: ra = plc;, p; - плотность, с; - скорость звука в жидкости.

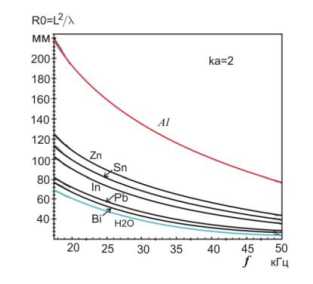
В данной работе были также произведены оценки величин ближней и дальней зоны излучения, а также толщины вязкого слоя для ряда расплавов металлов (рис.3а,Ь,с). Протяженность ближней зоны излучения - r₀ определяется выражением [5]:

Г о = п²/Л = d²f/(4q) ,

Протяженность дальней зоны - R 0 (зона Фраунгофера) определяется расстоянием от поверхности излучателя до первой фокальной точки, где интенсивность максимальная. Интенсивность в этой зоне изменяется в зависимости от квадрата расстояния [5].

Приведенные на рис.2a,b величины интенсивности, являются потенциально достижимыми для случая докавитационного режима. [5]. При развитии кавитации появление пульсирующих пузырьков приводит к изменению скорости звука и плотности возмущенной жидкости [10], а начальный этап развития кавитации в легкоплавких металлах зависит от смачивания и шероховатости поверхности излучателя [11-14].

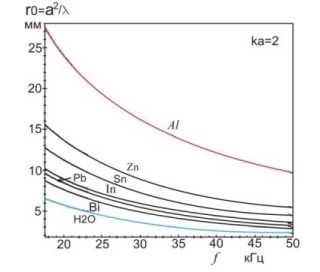
a                        b                       c

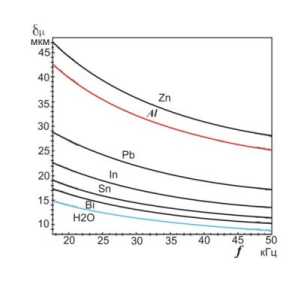
Рис. 3 a) Зависимость протяженности ближней зоны излучения – r0 , b) дальней зоны излучения - R0 от частоты для ряда легкоплавких металлов , с) толщина вязкого слоя - 8 ^ для ряда расплавов металлов.

Кавитирующая жидкость является нелинейной средой, характеризуемой средним значением сопротивления излучения ргсг, которое также как мощность ультразвука, передаваемая в жидкость нелинейно зависит от квадрата колебательной скорости D^ = (

W_ak = ^к^ = ~^_тPiC S [15]. Рассмотрение этого явления произведено в работах [11-14] и выходит за рамки данной работы.

Но исходная величина ka = 2 при расчете излучателя для случая введения ультразвуковых колебаний в жидкий металл на практике остается оптимальной [16].