Излучение звука сферой с переменной температурой

Известны механизмы излучения звука, нестационарными течениями [2,3,5], когда, звуковое поле является следствием вихревых турбулентных пульсаций. При малом числе Маха, нестационарное течение в области аэродинамических источников звука, может рассматриваться в приближении несжимаемой жидкости [4], и звук образуется за. счет динамических процессов в вихревом течении. При этом можно рассмотреть альтернативный механизм генерации, связанный с вязкой диссипацией в турбулентном течении, который обычно проявляет себя вблизи границ (так называемый константиновский механизм генерации/затуха-ния [6,7]). При неоднородности температуры также могут проявляться два. аналогичных механизма. [1]: один напрямую связан с теплопроводностью, другой связан с нестационарным переносом неоднородности температуры и может быть существенен в горячих турбулентных течениях (горячих струях). В настоящей работе рассматривается источник первого типа, связанный с теплопроводностью. Простейшей задачей, в которой реализуется источник подобного типа, имеющей к тому же важное методическое значение, является задача, о покоящемся шаре, поверхность которого имеет температуру, периодически меняющуюся

во времени. В таком случае течение в главном приближении является стационарным, а пульсации происходят за счет неоднородности температуры. В рассматриваемой постановке при учете малости колебаний температуры и компактности сферы как источника звука задача может быть решена точно.

Эффекты акустического излучения в случае неоднородностей температуры имеют прямое отношение к излучению шума горячими потоками, экспериментальное исследование которых до последнего времени было ограничено в силу отсутствия требуемой экспериментальной базы. Появление в акустическом отделении ЦАРИ стенда с горячим потоком в заглушенной камере [8] позволит проводить фундаментальные и прикладные исследования в области генерации шума неизотермическими потоками1.

2.    Постановка задачи

Пусть на поверхности сферы радиуса а заданы граничные условия на температуру:

Т (t, а) = Т а + Т‘е^-іш1.

Сфера погружена в вязкий совершенный газ, подчиняющийся уравнениям Навье -

Стокса:

' dp + дик = 0

dt   Р дхк    1

du. _   др д (     1 дик \

• ^Р dt      дх. ^Pdxj \ ^ij   3 дх_к^ij) ¹

• < dT  dp _ д2т       /       1 / дик V\

  
  

^{pC p} dt   dt = ^к дхк дхк ^{+ 2} у⁸^⁸'^-   3 (дхJ J

• р = pRT,

• _s. = 1 ( ^д' ₊ ""^ .

• _ ^-3    2 \dx-j    дх./

Здесь р,р,Т,и. — поля плотности, давления, температуры и скорости соответственно, с_р,K,p,R — известные постоянные. Граничные условия (прилипания и убивания возмущений, распространяющихся от сферы на бесконечность):

lim v(t, х1, х ₂ , х з ) = 0 ,

^(т =    ^х 1 ^{+ х} 2 ^{+ х} 3 ),

v |r = a

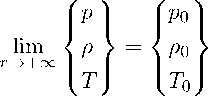
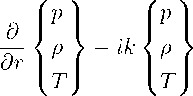
=" ш

т ^ +то.

Требуется решить задачу (1) - (3) и определить интенсивность акустических возмущений, создаваемых пульсациями температуры на сфере. Возмущения считать малыми.

Будем считать, что сфера — акустически компактный источник и справедливы соотношения

• к « ¹ « J^ =1,                         (4)

3.    Линеаризация задачи

а V х I где к = ш/с — волновое число, х = ^(срР-) ~ коэффициент температуропроводности.

Линеаризуем задачу, явно выделив возмущения относительно стационарного состояния:

Р ^ Р о + P, р ^ ро + р, T ^ Т о + Т,

и учтём, что среднее течение отсутствует (вязкостью можно пренебречь, см. [6]), а задача сферически симметрична:

др

+ poV • v = 0, at дг ро at = -^

дТ роСР ^

др А „

^- ді = ^{К Д Т} '

( р = poRT + pRTo.

4.    Получение уравнения для температуры

Из первых двух уравнений (5) стандартным образом можно исключить скорость:

• д2 Р - Др = 0. дТ²

Выразим плотность из уравнения состояния и подставим в (6):

7 д 2р с² дТ²

Р о д 2 Т

Др То дТ2,

С =^RTо,  7 = с,, с».

Продифференцируем (7) по времени:

7 д²   др        др\

С2 дт² (sty ^{- Д} (sty =

Р о д³Т

Т о at³.

Выразим из уравнения энергии производную давления по времени:

ЭР       дТ \ ai = РоСр ( л " хДТ)

и подставим её в уравнение (8):

^С рХ^Д 2 ^Т - (^х^ ^{+ с}

^ д^ж( 7Ср_  ^ д3Т-А

'^р дt) ^{ДТ +}( с²    Т о у st ^{3   0 .}

(Ю)

Учтём, что д дт ^ гш,

Т_ с2

-

1 _ 1

СрТо    с² .

Тогда уравнение (10) преобразуется:

Д2Т + (У + 7і2) ДТ + е Д2Т = 0.

(И)

5.    Общее решение уравнения для температуры

Если мы получим решение Т (г), то из уравнения энергии (9) сразу находим р(г). Удобно ввести замену Ғ (г) = гТ(г) после которой уравнение (11) на новую функцию Ғ с учётом сферической симметрии задачи будет иметь вид

Ғ ⁽⁴⁾ + (і ^— + ук²) Ғ‘‘ + і ^— к²Ғ = 0.

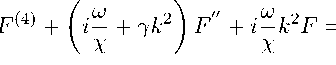
Это линейное обыкновенное дифференциальное уравнение четвертого порядка с постоянными коэффициентами. Его решение ищется в виде е^Хт, откуда

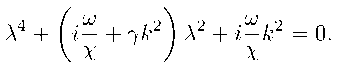
А⁴ + ^ і — + ук² ^ Л² + і—к² = 0

Решение этого биквадратного уравнения:

^Л 1 , 2 , 3 , 4 = ±

—            И .-—,9

( і —+ ук²) ±ы м—+ ук²) — 4і—к²

А общее решение уравнения (12) представляется в виде

Ғ = Сіе^х^^г + С2е^х2 + Сзе^ + С 4 е^Л4^г

Для определения констант используем условия на границе сферы (закон изменения температуры и условие прилипания) и на бесконечности (условие излучения и убывания).

6.    Удовлетворение условиям излучения и убывания

Чтобы использовать условия на бесконечности, необходимо знать представление комплексных чисел в алгебраическом виде Л = а + ib. Такое представление можно получить путём разложения корней по формуле Тейлора (используя (4)):

—                —            .-—,9

і—+ ук² ± a і—+ ук²   — 4і—к²

X             X ) X

=^— (д ^{+ ук} 2 ) ±У—1 )

+ (ук2)2 + 2і—ук2 — 4і —к2

(х ^{+ ук}2) ± д/

X

1 + 2і ^Х к²(2 — у)

—

—(д+ук2) ±(

X

—

і —

X

к2(2 — у) . (13)

Таким образом,

Л 1 , з = ±\/—к² = ±ік,

^Л 2 , 4 = ±^^{—і— — к} 2 ^{( у —} 1) ^ ± ^{(1 —} ^^Х ^{— (1+} ^ ^Т^{( у} — 1) = ±⁽".)

Чтобы удовлетворить условию излучения, мнимая часть должна быть положительной, а условие убывания требует отрицательной действительной части, поэтому

Ғ = гТ = С1е^ікг + С ₂ е ^{- (}-^)г

Отметим, что если пренебречь слагаемым в показателе экспоненты порядка к²^ x/—> то из граничных условий на сфере будет видно, что С1 = 0. Это означает, что акустические возмущения в главном приближении отсутствуют, и для их определения необходимо в разложении удерживать и члены более высокого порядка.

• 7.    Удовлетворение условиям на сфере

Граничное условие на температуру даёт aT ‘ = Ci + 62,

61 = 61 exp

(-a(1 — ^/IX + a(1 + г)VIR^7 — 1)) ,

6₂ = 6₂ ехр(гка).

Условие прилипания можно переписать в терминах давления, используя линеаризован ное уравнение импульсов:

v(t, a) = 0

dv     Эр

Ро dt     дт

^    (t,a) = 0.

дт

Подставим найденное общее решение (14) в уравнение энергии, чтобы найти давление:

• -гшр    .     х ^д2F

  ---- = -гш^т---т—у .

роСр             т дт2

Опустим несложные, но громоздкие выкладки и запишем для давления окончательно:

• — та ⁶¹ гк^{2X (}7 - ^1)exp ^^-т(1 - ^г)Лтр- ^{+ т(1 + г)}^^2ХД-⁽7 ^— 1/1 ⁺

РоСр    т ш                        2-              ш 4

+ — (1 + гк^2X ) ехр(гкт). (17) т \ ш

Условие (16) даёт второе равенство для определения констант:

61 У(7 - 1)(1+ 9+62^ =0.

Решение системы (15), (18):

61 ~ T‘а, 6₂ та —T ‘(7 — 1)k²aJX exp (г—) .

• 8.    Результаты

Таким образом, пульсации давления

р(t,т) = Р_о^ae ^гш1 |г(к1)² • exp (———(^——) — к² al • exp (гк(т — a) + г— )|    (19)

и температуры

T (t, т) = T ‘-е ^гш1 <(exp (—----^^-----) — k²al(y — 1) • exp (гк(т — a) + г— ^ j> ,    (20)

где Ро = pocpT‘(7 — 1), l = ^yх/ш. Первый экспоненциально убывающий член в (19) всю ду много меньше второго звукового члена, поэтому им можно пренебречь. Оставшийся

звуковой член с учётом ср(7 — 1) = c2/To запишется в виде

Р

Рос2

-

IT'

т^ ^{(ka) e}xp(

—гшt + гк(т

-

—

^{a) + г} 4).

Такой же результат был получен в [1] на основе акустической аналогии Блохинцева - Хоу.

Мощность акустического излучения:

I = 4тгг²;|ф   2г ( ^Т) a²poc³(ka)²(kl)².

2рос      \T0J

В дополнение скажем, что приближенно решить рассматриваемую задачу можно «более физично». Пульсации температуры на сфере приводят к пульсациям объёма газа вблизи неё (тонкий слой газа около стенки). Эти пульсации легко оценить, зная коэффициент объемного расширения /3 и характерную толщину приповерхностного слоя l = ХІ^ші ^в который подводится тепло:

V = ¹   • V^dT_; ^ ³ • ^4га2¹ • ^dT = -A^V^x' exp f-гші + г|) .       (23)

V о! ОТ               ОТ                'о \         2)

Тогда по известным формулам (см. [6]), используя (23), находим выражения для давления

p(t,r) = Ро/^~ to —рос2-^-(ka)2exp(-i^t + ikr) 4гг            г То и мощности излучения

I = ^P°^V" ~ 2г () а²ро c³(ka)²(kl)², 4гс      ТТ₀

что соответствует (22).

9.    Заключение