Изменение контактных углов смачивания при добавлении в моющие растворы поверхностно-активных веществ

В основе комплекса параллельнопоследовательных физико-химических и физико-механических процессов, объединенных в многоэтапном технологическом процессе отмывания загрязнений, лежат явления смачивания, адсорбции, диспергирования-эмульгирования, стабилизации и гетерокоагуляции дисперсий, пептизации, адгезии, набухания, растворения, солюбилизации и пено-образования. Наиболее важная роль в протекании процессов отводится природе очищаемой поверхности; загрязнениям; среде, в которой проводится очистка; моющим средствам; способам и интенсивности механического воздействия. Начальная фаза процесса отмывания загрязнений заключается в смачивании или вытеснении жидкой фазой другой фазы (твердого или жидкого тела). Эффективность процесса напрямую зависит от контакта моющего средства с обмываемой поверхностью. В начале смачивания частицы гидрофильных загрязнений намокают, увеличиваются в объеме и начинают разрушаться. При полном смачивании они растекаются равномерным слоем по поверхности и удаляются струей воды или механическим способом. Для смачивания и удаления гидрофобных частиц (частиц нагара, масел, смол, песка и т. п.) моющая жидкость должна содержать поверхностно-активные вещества (ПАВ). Общеизвестно, что мерой смачивания обычно служит контактный угол θ , поскольку он является мерой относи-

Technologies and means of maintenance in agriculture

тельного притяжения жидкости к твердому телу и к самой себе [1]. Чем активнее моющая среда в физико-химическом плане, тем меньше затрат механической энергии требуется для удаления загрязнения, а чем среда пассивнее, тем больше нужно затрат [2]. Поэтому оптимальные параметры моечного процесса выбирают на основе технологических и экономических соображений. Одновременно необходимо отметить еще один немаловажный показатель моющего раствора: способность формировать на очищаемой поверхности защитную пленку, и как следствие, повышать коррозионную стойкость обмываемой поверхности без дополнительной консервационной обработки. Итак, поскольку смачиваемость является одним из показателей физикохимических свойств моющих растворов, важно иметь сведения о влиянии ПАВ на величину контактного угла.

Целью исследования является определение функциональной зависимости контактного угла смачивания от концентраций различных комбинаций ПАВ. Для реализации цели исследования авторами разработана методика экспрессного определения контактного угла смачивания и программное обеспечение, автоматизирующее процесс и ускоряющее обработку информации.

Обзор литературы

Процедура определения контактного угла смачивания имеет ряд особенностей [3], без учета которых точность его определения довольно низка (ошибки от 1 до 5 градусов), а учет влияния ПАВ 297

оказывается затрудненным из-за того, что отклонения в величине контактного угла имеют тот же порядок, что и ошибки измерения. Более того, существенный разброс значений появляется из-за явления гистерезиса контактного угла, связанного с разными значениями угла при натекании (росте капли) и отте-кании (уменьшении капли) [4–8]. Размер капли также может оказать влияние на результаты измерений, поэтому необходимо использовать рекомендации по выбору их размера из определенного диапазона.

• А. Мармуром [9] разработана обобщенная методика определения контактных углов смачивания: даны рекомендации по кратности проведения экспериментов, объему капли, скорости увеличения и уменьшения объема капли. Для определения угла смачивания применяется микроскоп, который использует каплю жидкости в качестве чувствительного элемента.

Учет возникающих сложностей при измерениях приводит к тому, что процедура измерения контактного угла может потребовать нескольких часов [Там же], однако в связи с непрекращающими-ся физико-химическими процессами в моющей жидкости ее свойства за это время могут изменяться, что способно повлиять на точность измерений.

Поскольку при простом измерении контактного угла возникает множе-

Том 29, № 2. 2019

ство нюансов, мешающих быстрому и точному его определению, были рассмотрены методы установления геометрической формы капель и их аналитического описания [10–16]. Основой данных методов является минимизация поверхностной энергии поверхностей раздела фаз. В работе С. И. Матюхина и К. Ю. Фроленкова [17] приведен обзор основных методов расчета равновесной формы капель, расположенных на твердой горизонтальной поверхности в гравитационном поле: приближенные методы описания формы капель, вариационные методы и т. д. Численное решение уравнения Лапласа позволяет получить выражения для формы капли, которые содержат только геометрические параметры (геометрия капли определяется силами поверхностного натяжения и силой тяжести). Классический вид формы капли на горизонтальной поверхности показан на рис. 1 [Там же].

Еще Юнгом была показана связь краевого угла с соотношением между удельными поверхностными энергиями раздела разных фаз. Согласно вышеназванной работе [Там же], равновесная форма осесимметричных капель может описываться дифференциальным уравнением следующего вида:

z"                 z'

--------+-- 177 = 2b + cz , (1) a          ^{3/2                  1/2}

+ z '2)      x (1 + z '2)

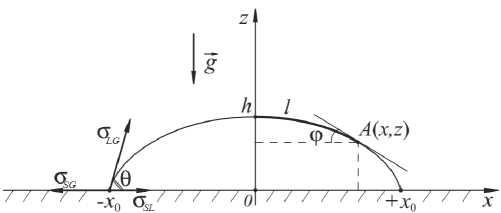
Р и с. 1. Классический вид формы капли на горизонтальной поверхности: σ_LG – коэффициент поверхностного натяжения жидкости; σ_SG – удельная поверхностная энергия раздела твердой и газообразной фазы; σ_SL – удельная поверхностная энергия раздела твердой и жидкой фазы

F i g. 1. The classic type of a drop shape on a horizontal surface: σ_LG is the coefficient of liquid surface tension; σ_SG is the specific surface energy of the solid and gaseous phase; σ_SL is the specific surface energy of the solid and liquid phase

298                    Технологии и средства технического обслуживания в сельском хозяйстве

Vol. 29, no. 2. 2019 где x и z – координаты, b и c – коэффициенты.

В качестве граничных условий уравнения (1) выступают краевой угол и объем капли. Производная z ʹ( x ₀) есть тангенс угла наклона, а следовательно, и искомый контактный угол. Таким образом, появляется возможность достаточно быстро определять форму огибающей для поверхности капли z ( x ), и уравнение (1) можно использовать в экспрессном методе определения контактного угла смачивания.

Итак, анализ литературных источников показал, что для повышения точности измерений и скорости вычислений контактного угла смачивания необходимо объединить достоинства чисто экспериментальных методов с теоретическим описанием кривой поверхности капли и использовать вычислительные мощности современных устройств и программных средств.

Материалы и методы

Определение контактного угла смачивания в данной статье основывается на статистической обработке фотографии капли моющего раствора на горизонтальной поверхности специально созданной программой. Программа позволяет получить достаточно большой массив данных для описания z(x). Данные поступают от попиксельно обрабатываемой фотографии путем сравнения цветов фона, капли и поверхности. Такой подход дает возможность получать достаточно высокую точность определения граничных координат поверхностей раздела фаз, поскольку ошибка колеблется в пределах 2–3 пикселей с промежуточными переходными цветами. Далее массив данных передается системе компьютерной алгебры wxMaxima, в которой, согласно дифференциальному уравнению, подбираются числовые параметры формы капли z(x) и затем вычисляется производная zʹ(x0). Поскольку процесс фотографирования и обработки данных не требует больших затрат времени, в целях повы- шения статистической надежности для каждого варианта комбинаций ПАВ и их концентраций были вычислены контактные углы в двадцатикратной повторности, средние значения которых приведены в таблице.

В настоящее время для повышения моечного эффекта используются такие синтетические моющие средства (СМС), как Лабомид-203, МС-8, МЛ-51 и др. Они представляют собой смесь ПАВ с электролитами – натриевыми солями угольной, фосфорной и кремовой кислот. Моющее действие (процесс удаления загрязнения с поверхности твердых тел с переводом его в состояние раствора или устойчивой дисперсии) растворов СМС, применяемых для очистки поверхностей, определяется комплексом их свойств.

Для изучения связи между углом смачивания Y и концентрациями X ₁ (МБК), X ₂ (Лабомид-203), X ₃ (МС-8) и X ₄ ¹ (МЛ-51) воспользуемся нелинейным множественно-регрессионным анализом, который позволяет:

‒ построить нелинейную модель с большим числом факторов;

‒ определить и сравнить степени влияния различных факторов в отдельности на моделируемый показатель;

‒ выделить непосредственное влияние факторов на результативный признак и косвенное влияние фактора (через другие факторы) на результат;

‒ выявить существенность влияния отдельного фактора (или группы факторов) на результативный признак на фоне других факторов и т. д.

Наиболее подходящей в данном случае является мультипликативная степенная функция, впервые примененная в 1929 году Ч. Коббом и П. Дугласом:

Y = AX ₁ ^α X ₂ ^β X ₃ ^γ X ₄ ^δ , (2)

где Y – угол смачивания, град.; X_i – концентрации ПАВ, %; A , α , β , γ , δ – неизвестные параметры.

Функция (2) однородна со степенью однородности p = α + β + γ + δ :

Т а б л и ц а T a b l e

Q GO о fl О Ь fl fl о U и s и w s fl fl fl fl fl fl 5	1 2	o.	saajSap ‘a^SuB Slippy / izBdj ‘кинвниьвиэ eojx	oo +1 oo	+1 ^D	+1 ^D	+1	+1	+1
			a ‘XjqiqBjPM / а ‘члэоиэвниьвиэ	oo 04	OO	O\ (M	O\	о	О
		of	saajSap ‘a^Sire Slippy / IzBdj ‘кинвниьвиэ eojx	of +1 fl	rf +1	^ of +1	rf +1	°4 +1	+1
			a ‘XjqiqBjPM / а ‘члэоиэвниьвиэ		^D	O\			(M
		o.	saajSap ‘a^Sire ошпадх / IzBdj ‘кинвниьвиэ eojx	oo of +1	of +1 ^D ^D	rf +1	rf +1	rf +1	rf +1
			a ‘XjqiqBjPM / а ‘члаоиэвнинвиэ	о	o			fl
	oo GO 2 OO 6	o.	saajSap ‘э^Зив Slippy / №dj ‘кинвниьвиэ eojx	+1	+1	+1 СЧ	+1 Si	°4 +l	°4 +1
			a ‘XjqiqBjPM / а ‘члаоиэвниьвиэ	о	fll	fl	^D	oo	oo
		of	saajSap o|Sub Slippy / №dj ‘кинвниьвиэ eojx	oo +1 fl	+1 fll	+1 O\	+1	+1	+1 oo
			a ‘XjqiqBjPM / а ‘чхэоиавниьвиэ	Я	r5	^D (M	oo	о	m
		o_	saajSap o|Sub Slippy / №dj ‘кинвниьвиэ eojx	04^ of +1	of +1	rf +1	+1	+1	+1 oo
			a ацццеиэлх / а ‘чхэоиавниьвиэ		oo	O\			(M
	s "fl § о 3 s s о VO fl 4	o.	saajSap o|Sub Slippy / №dj ‘кинвниьвиэ eojx	°4 +1 ^D	+1	+1 oo	+1	+1	+1
			a ацццвиэлх / а ‘чхэоиавниьвиэ	OO (M	O\	о	m		(M
		of	saajSap o|Sub Slippy / №dj ‘кинвниьвиэ eojx	^ of +1	of +1	^ +1 O\	°4 +1	+1	+1 O'!
			a ацццвиэлх / а ‘чхэоиавниьвиэ		O\		(M	Si	Si
		o.	saajSap o|Sub Slippy / №dj ‘кинвниьвиэ eojx	rf +1	rf +1	rf +1 O\	^ of +1	of +1	+i
			a ацццвиэлх / а ‘чхэоиавниьвиэ				^D	^D
%				o'	*4	o'	o"	o"	'fl

• -    при p = 1 имеется линейная однородность, т. е. постоянная эффективность при увеличении средних значений концентраций;

• -    при p > 1 имеется рост эффективности, т. е. с увеличением средних значений факторов в t раз угол смачивания меняется в t·p раз;

• -    при p < 1 наблюдается падение эффективности.

Параметры α , β , γ , δ показывают процентное изменение угла смачивания, вызванное изменением концентрации соответствующего ПАВ на 1 % при неизменных значениях концентраций других ПАВ. Если в общем случае они зависят от X_i , то для рассматриваемой функции (2) они постоянны.

Функция (2) может быть оценена с помощью нелинейной регрессии, реализующейся в большинстве офисных пакетов прикладных программ (MS Excel, LibreOffice Calc и др.).

Результаты исследования

Исследования влияния концентраций МБК и СМС на изменение контактного угла смачивания проводились в следующих комбинациях: МБК и Ла-бомид-203, МБК и МС-8, МБК и МЛ-51. Статистическая обработка дает следующие результаты.

С коэффициентом детерминации R ² = 0,91 определена зависимость

Y = 70,23428 X ₁ ^–0,1681 X ₂ ^–0,372253 . (3)

Из выражения (3) следует, что увеличение среднего значения X ₁ на 1 % приведет к уменьшению среднего значения угла смачивания на 0,1681 %, а увеличение среднего значения X ₂ на 1 % – к уменьшению среднего значения угла смачивания на 0,37225 %, т. е. увеличение концентрации Лабомид-203 оказывается более выгодным. Однако, так как |–0,3722533 – 0,1681| = 0,54035 < 1, получаем убывающую отдачу от увеличения концентрации ПАВ.

Аналогично с коэффициентом детерминации R ² = 0,92 определена зависимость

Y = 64,8027 X ₁ ^–0,28602 X ₃ ^–0,49342 . (4)

Из выражения (4) следует, что увеличение среднего значения X 1 на 1 % приведет к уменьшению среднего значения угла смачивания на 0,28602 %, а увеличение среднего значения X ₃ на 1 % – к уменьшению среднего значения угла смачивания на 0,4934 %, т. е. увеличение концентрации МС-8 оказывается более выгодным. В данном случае |–0,49342 ‒ – 0,28602| = 0,77944 < 1, т. е. функция также показывает убывающую отдачу от увеличения концентрации ПАВ.

С коэффициентом детерминации R ² = 0,92 определена зависимость

Y = 74,4352 X ₁ ^–0,14296 X ₄ ^–0,33504 . (5)

Получается, что увеличение среднего значения X ₁ на 1 % приведет к уменьшению среднего значения угла смачивания на 0,14296 %, а увеличение среднего значения X 4 на 1 % - к уменьшению среднего значения угла смачивания на 0,33504 %, т. е. увеличение концентрации МЛ-51 оказывается более выгодным. Поскольку |–0,33504 – - 0,14296| = 0,478 < 1, то функция показывает убывающую отдачу от увеличения концентрации ПАВ.

На рис. 2 показаны функции изменения контактного угла смачивания для перечисленных трех случаев.

Обсуждение и заключение

Во всех рассмотренных случаях получаем убывающую отдачу величины контактного угла смачивания от увеличения концентрации ПАВ независимо от того, какую комбинацию компонентов использовали. Данный факт говорит о том, что концентрации ПАВ превысили то граничное значение, когда они давали возрастающую

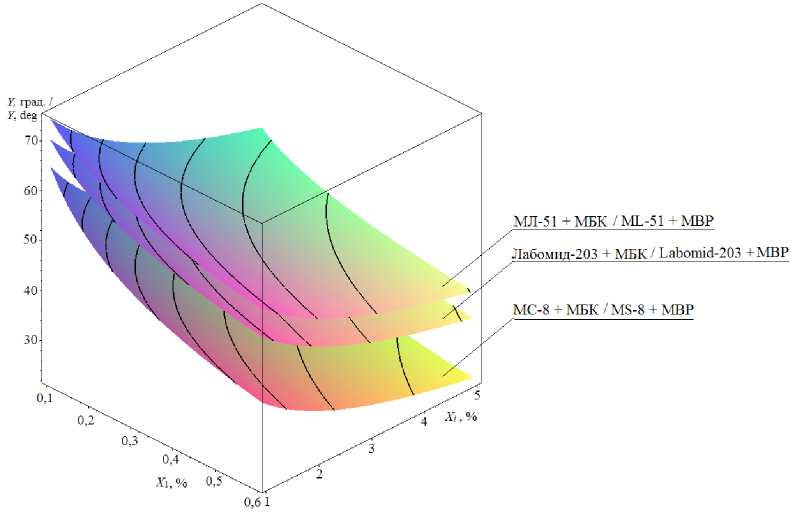
Р и с. 2. Изменение контактного угла смачивания F i g. 2. The change of contact wetting angle отдачу от увеличения их содержания в моющем растворе. Таким образом, можно сделать вывод, что для рассмотренных комбинаций процентное содержание ПАВ избыточно. Кроме того, стало ясно, что влияние МБК наиболее эффективно в паре с МС-8, поскольку в результате дает наибольшее из всех случаев уменьшение угла смачивания (0,28602 %) и, как следствие, наиболь- шее (0,77944 %) совместное влияние из всех рассмотренных комбинаций ПАВ.

Полученные результаты позволяют на стадии проектирования технологического процесса мойки для различных вариантов комбинированного использования ПАВ рассчитать и оптимизировать их процентное содержание, определяющее качество процесса мойки и его производительность.

Все авторы прочитали и одобрили окончательный вариант рукописи.