Изменение траектории наборов пучков Эйри с помощью несущих пространственных частот

Особые свойства пучков Эйри [1], такие как сопротивление влиянию дифракции и распространение в свободном пространстве по параболической траектории [2–4], обусловили повышенный интерес к их применению во многих областях [5], включая оптическое манипулирование [6–8], микроскопию [9, 10], углубление фокуса оптических систем [11 – 13], лазерную обработку [14, 15] и оптическую маршрутизацию [16].

Так как функции Эйри, подобно функциям Бесселя, являются бесконечно протяжёнными, для их физической реализации требуется усечение. Чаще всего ограничение достигается умножением функции Эйри на экспоненциальную [2] или Гауссову [17] функцию. В обоих случаях формируемые пучки фактически перестают быть бездифракционными, хотя приблизительно сохраняют свой вид до некоторого расстояния. В работе [18] был рассмотрен иной способ усечения бесконечной функции Эйри – с помощью прямоугольной апертуры, усекающей функцию в положительной части аргумента при спадании её практически до нуля, а в отрицательной части до n -го нуля. Такие пучки демонстрируют сохранение своей структуры на значительно больших расстояниях.

Свойство ускорения пучков Эйри используется для формирования пучков с резкой автофокусировкой [19, 20] за счёт их зеркальной или круговой симметризации [21 – 23]. Востребованность пучков со свойствами автофокусировки в различных приложениях [24–26] стимулирует учёных к поискам новых модификаций и обобщений таких пучков [27–31].

Одним из подходов к расширению типов и разнообразию структуры автофокусирующихся пучков является формирование наборов или кластеров разных пучков [32 – 37].

В частности, в работах [36, 37] было исследовано распространение наборов пучков Эйри, которые обладают свойствами ускорения как отдельных элементов набора, так и всей структуры в целом. Отметим, что каждый из пучков в наборе может иметь дополнительные пространственные несущие частоты, меняющие характер траектории отдельных элементов кластера и, следовательно, свойства автофокусировки всего кластера в целом.

В настоящей работе теоретически и численно исследуются свойства автофокусировки наборов пучков Эйри–Гаусса с различными несущими пространственными частотами. При этом также варьируются параметры как самих пучков, так и всего набора. Рассматривается поведение набора, составленного из пучков, каждый из которых повёрнут на произвольный угол, а также поведение самих наборов, повёрнутых на определённый угол вокруг своей оси.

Моделирование выполнено с использованием дробного преобразования Фурье [38, 39], описывающего параксиальное распространение лазерного излучения через линзовые системы.

• 1.    Описание метода моделирования

Многие свойства распространения лазерных пучков в оптической системе можно получить, зная функцию амплитуды входного поля и ABCD-матрицу, опи- сывающую данную оптическую систему [40]. Если AD – BC = 1, то существует линейное каноническое

F ( u , v ) = —— f ( x , У ) exp!— Г A ( x ^{2 v !} 2n B³ --" ^v ' [2 B ^{L v}

преобразование, связывающее входное и выходное поля, известное в оптике как интеграл Коллинза [41]:

+ y2)- 2 (xu + yv) + D (u2 + v2)] ^ dx dy.

В формуле (1) k =2 п / X - волновое число, мм^-1, X -длина волны, мм.

При определённых значениях элементов ABCD-матрицы можно получить частные случаи интеграла Коллинза – преобразование Фурье, которое применяется для разложения светового поля на плоские волны по частотам; преобразование Френеля, использующееся для описания распространения света в свободном пространстве; а также дробное преобразование Фурье, которое широко используется в квантовой механике для решения физических задач с применением уравнения Шрёдингера. Дробное преобразование Фурье (ДрПФ) также позволяет рассмотреть распространение света в градиентном оптическом волокне [42], а также в оптических системах из нескольких сферических и /или цилиндрических линз [43]. В данной работе интеграл Коллинза используется для моделирования системы, включающей в себя обобщённые линзы [44].

Для ДрПФ коэффициенты A , B , C , D имеют следующий вид:

Г     nz

cos

Г AB ^

I C D )

2 f

n z ^ f sin

2 f

ⁿ z sin

2 f

f

cos

n z

2 f

где f – фокусное расстояние, мм, z – расстояние до плоскости изображения, мм.

Сами пучки Эйри Ai( x , y ) задаются следующим образом:

Ai ( x , y ) = 3 { exp Г i ( a u 3 + в v 3 + a ₀ u 0 + в ₀ v 0 ) ] } . (3)

В формуле (3), приведённой выше, используется преобразование Фурье 3 { . }, применённое к комплексной экспоненте, содержащей кубические и линейные компоненты, которое в результате задает моду Эйри. Коэффициенты a , в - параметры масштаба (мм ³ ), которые влияют на размер главного «лепестка» моды Эйри, a o , в о - смещения относительно центра входной плоскости (мм). Придавая коэффициентам различные значения, можно изменять траекторию распространения пучков. Для ограничения пучка используется функция Гаусса, в которой σ играет роль радиуса усечения. Таким образом, получаем формулу (4) пучка Эйри–Гаусса:

Г x ² + y ² ^

^f ( x , y ) = Ai ( x , y ) exp I--— I .                 ⁽⁴⁾

Для поворота пучка или набора пучков используются следующие формулы:

[f(xr,yr), xr e[-a,a], yr e[-b,b], frol (x, y ) = S

[0, иначе, xr = x cos ф-y sin ф,(6)

yr = x sin ф + y cos ф .(7)

В формулах (5– 7) f rot – повёрнутая мода, ( x r , y r ) – вычисленные координаты для новой точки ( x, y ), соответствующие точке неповёрнутой моды. В случае, если новые координаты выходят за пределы массива, значение в данной точке приравнивается к нулю; φ – угол, на который необходимо повернуть моду против часовой стрелки; [– a , a ] и [– b , b ] – интервалы (в мм) по осям x и y соответственно, на которых строится входное поле пучка или набора пучков.

Наборы пучков формируются по приведённой ниже формуле:

N fcih-se^r ( x, y ) = ^ f (x -pcos фn, y -p sin фn )x

П 2Т                                      (8)

x exp Г- i ^ ( x cos ф _n + y sin ф _n ) ] .

В формуле (8) вводится несколько дополнительных параметров, необходимых для формирования набора пучка. N – количество пучков в кластере, ρ – радиус кластера, мм, ф _n 2 п n / N - угол между пучком в наборе и осью x , ξ – параметр несущей пространственной частоты, мм^–1. Множители при x и y в показателе экспоненты выбраны так, чтобы «проекции несущей» были пропорциональны проекциям радиус-вектора центра n -го пучка. Это обеспечивает сохранение симметрии кластера.

Хотя численное моделирование в параграфе 2 выполнено для выражения (8), теоретический анализ рассмотрим для одномерного одиночного пучка Эйри вида:

E ₀ ( x ) = Ai I x—x ⁰- 1 exp ( iax ).                      (9)

X s J

Такой подход позволяет качественно описать распространение каждого отдельного пучка из кластера. Так как каждый пучок разделим по координатам, то можно применить одномерный подход в плоскости, проходящей через оптическую ось и начальную точку пучка. При этом отсутствие Гауссова множителя приведет лишь к небольшим количественным отклонениям.

Таким образом, далее функция Эйри определяется как [1]:

х 1 Г I tt 3 . I .

^Ai( p ) = — exp l i— + ipt I d t .

2-      I 3 J

Можно убедиться, что параметры в (9) выражаются через параметры, введённые выше, следующим образом:

x 0 = ^а 0 ;

a = -£.

На основе (9), (10) можно получить выражение для амплитуды пучка на произвольном расстоянии

A I ⁵ 2 ku x 0

E ( u , z ) = V i no ² ■ Ai l

( 2 5 z s

54 I

16 s ⁴ J

x exp

( 5 4   ku   5 ²        5 ²   k ² u ² 5 ⁶ I

-               - x o               _

( 8 s ³   z   4 s ³        4    z ²     96 s ⁶ J

где

1 kk

5 2 = 2 z 2 f'

Выражение (12) получено при a =0 (в отсутствие несущей), иначе надо заменить u на u –( az / k ).

Максимальное значение функции Ai( p ) достигается при значении p 0 ≈ –1,02. Приравнивая аргумент функции Эйри в (12) этому числу, получаем уравнение траектории, по которой движется максимум амплитуды. В развёрнутом виде уравнение траектории следующее:

I        x ₀ I f - z z²

u = l P 0 + I s--+

I s J f 4 k ² s ³

f

^f - ^z

az

+ . k

Выражение (13) можно переписать в виде:

z2 a u = A(f - z) + B ~--+ 7z, f - z k

где

л I Xo I s A = l P0 + — I-

B =      .

4 k ² s ³

Из выражения (14) можно определить расстояние, на котором траектория пучка пересечет оптическую ось (т.е. произойдет фокусировка вне фокальной плоскости линзы). Это расстояние определяется из равенства u =0:

z

axis 1,2

= f ■

(A - C) ± Dd

2( B - C )

где C =( a / k )– A , D =( C – A )²–4 A ( B – C ).

Предполагается, что хотя бы одно из значений z ₁ ^a _, ^x ₂ ^is имеет физический смысл, т.е. является вещественным и положительным. Иначе траектория не пересекает оптическую ось. Следует отметить, что фокусировка здесь понимается не вполне в стандартном смысле: увеличения амплитуды отдельного пучка в этой точке не происходит. Но при определённом рас-

положении начальных центров смещенных пучков кластера все они пересекут оптическую ось в одной точке , благодаря чему произойдёт увеличение амплитуды. Поэтому мы называем такой эффект фокусировкой кластера в целом.

2. Результаты моделирования

Хотя полученные аналитические выражения позволяют вычислять распределения в различных плоскостях без численного интегрирования, однако с учетом необходимости сложения нескольких пучков их удобнее использовать для анализа свойств кластеров, а не для моделирования. Для расчета распределения формируемых полей как в поперечных, так и в продольных сечениях были использованы быстрые алгоритмы расчета [42, 43, 45]. Применим дробное преобразование Фурье к наборам пучков Эйри–Гаусса, сформированных по формулам (3), (4), (8) с помощью формулы (1), используя значения (2). Во всех случаях использовались следующие параметры моделирования: a = b = 4 мм, a = 1 мм, p = 2 мм, N =3, X = 633 нм, f = 1000 мм.

Рассмотрим распространение набора пучков Эйри-Гаусса в свободном пространстве в случае ^ = 0. Ниже показаны результаты моделирования кластеров пучков Эйри для параметров (здесь и далее размерность не указывается): a = в = 1, а о = в о = 0 (рис. 1), а = в = 5, а о = в о = 0 (рис. 2), а = в = 5, а о = в о =1 (рис. 3) и а = в = 5, а о = в о = -5 (рис. 4).

Сравнивая рис. 1 и 2, можно заметить, что увеличение параметров а , в приводит к увеличению размера главного «лепестка» пучка Эйри–Гаусса, но при этом остальные «лепестки» уменьшаются в размере. а о , в о позволяют задавать смещение пучка в плоскости. При этом получается, что отрицательные значения двигают пучок так, что в область максимума Гауссовой функции главный «лепесток» попадает лишь частично и пучок в основном состоит из дополнительных «лепестков».

Отметим, что наличие линзы изменяет траекторию максимума: она не очень похожа на параболическую, по которой пучок Эйри изгибается в свободном пространстве. Это показывает и выражение (13), имеющее вид дробно-рациональной функции.

Примем в дальнейших исследованиях а = в = 5, а о = в о = -5. Рассмотрим теперь случаи ^ = 6 (рис. 5) и ^ = - 6 (рис. 6).

Увеличение параметра несущей пространственной частоты ξ приводит к более ранней (на расстоянии z = 800 мм вместо z = 1000 мм в случае ^ = 0) и более резкой фокусировке (интенсивность осталась сосредоточенной в области главного «лепестка»). Использование отрицательного значения ξ также позволяет произвести такую же резкую фокусировку, но уже на расстоянии z = 1200 мм. Теоретический расчёт по формуле (15) даёт соответственно 804,6 мм (при ^ = 6) и 1321 мм (при ^ = - 6).

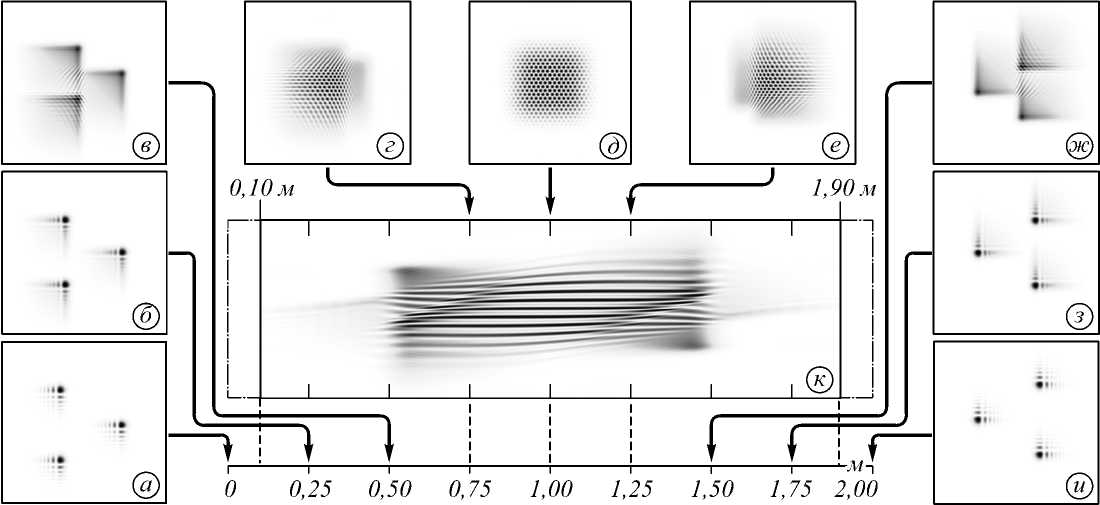
Рис. 1. Распределение интенсивности набора пучков Эйри–Гаусса с параметрами ξ = 0, α = β = 1, α 0 = β 0 = 0 на различных расстояниях: а) z = 0 м, б) z = 0,25 м, в) z = 0,5 м, г) z = 0,75 м, д) z = 1 м, е) z = 1,25 м, ж) z = 1,5 м, з) z = 1,75 м, и) z = 2 м, к) продольное распределение интенсивности на интервале z = 0,1...1,9 м

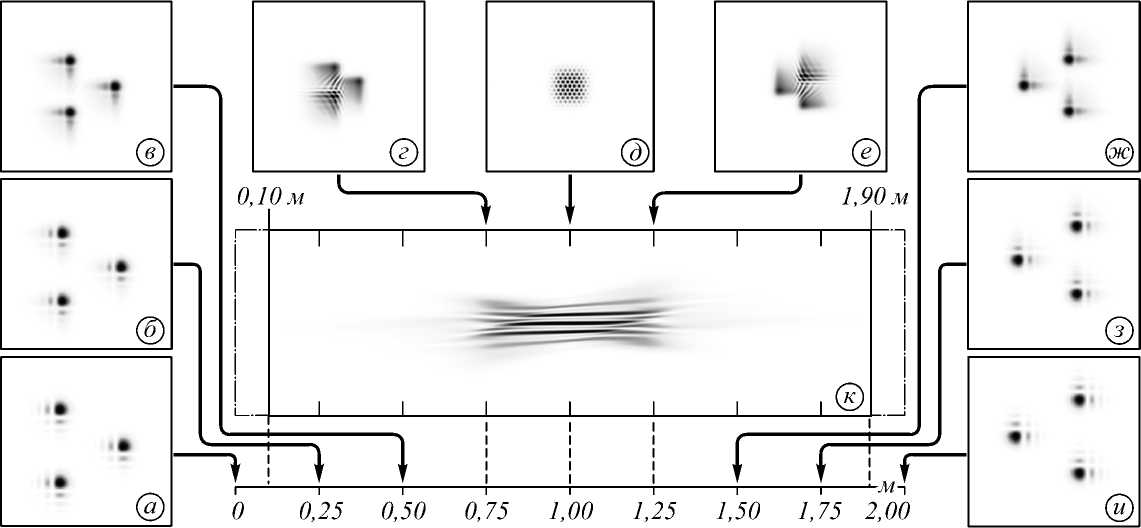
Рис. 2. Распределение интенсивности набора пучков Эйри–Гаусса с параметрами ξ = 0, α = β = 5, α 0 = β 0 = 0 на различных расстояниях: (а)–(и) расстояния, как на рис. 1, (к) продольное распределение интенсивности на интервале, как на рис. 1

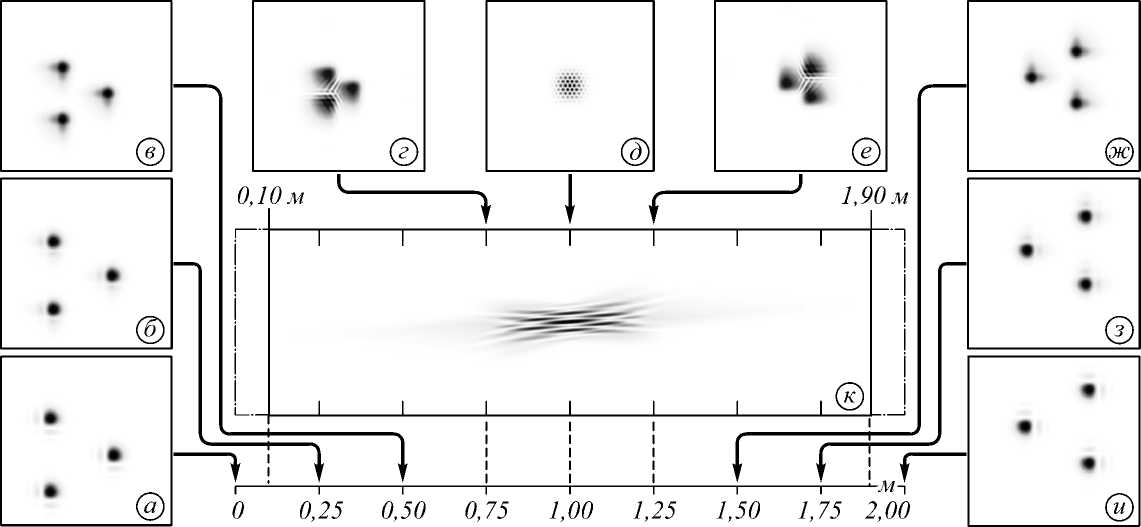
Рис. 3. Распределение интенсивности набора пучков Эйри–Гаусса с параметрами ξ = 0, α = β = 5, α 0 = β 0 = 5 на различных расстояниях: (а)–(и) расстояния, как на рис. 1, (к) продольное распределение интенсивности на интервале, как на рис. 1

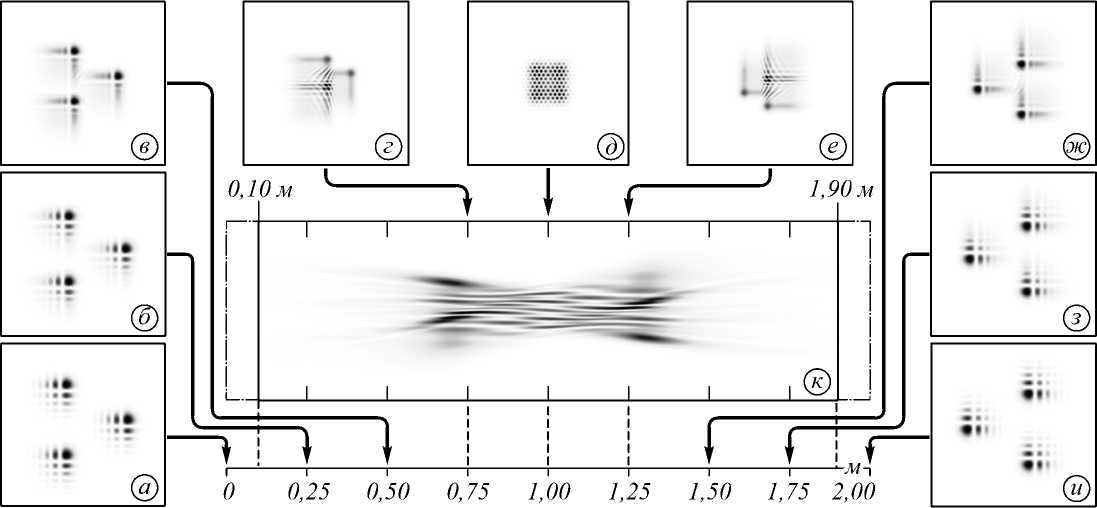
Рис. 4. Распределение интенсивности набора пучков Эйри–Гаусса с параметрами ξ = 0, α = β = 5, α 0 = β 0 = – 5 на различных расстояниях: (а)–(и) расстояния, как на рис. 1, (к) продольное распределение интенсивности на интервале, как на рис. 1

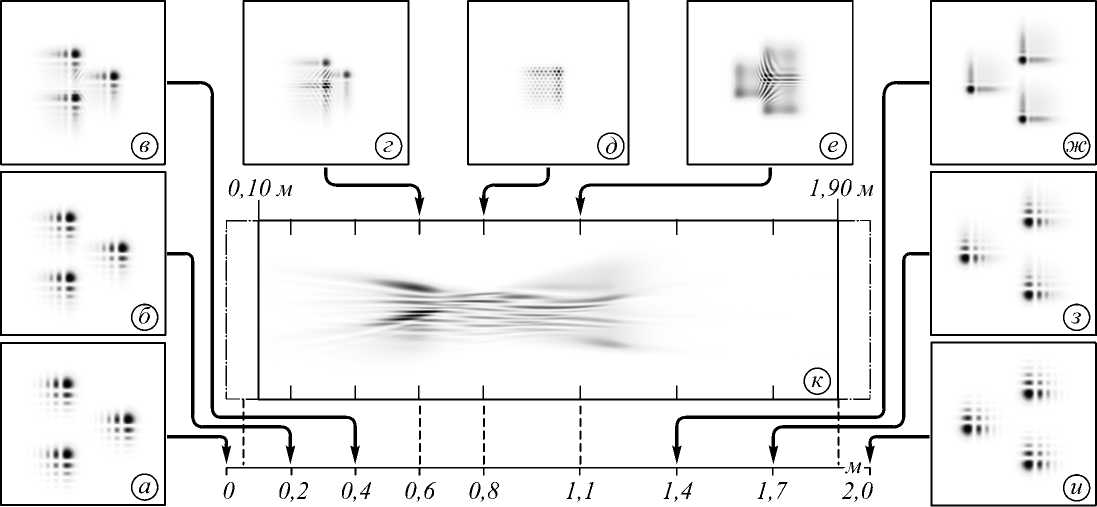
Рис. 5. Распределение интенсивности набора пучков Эйри–Гаусса с параметрами ξ = 6, α = β = 5, α 0 = β 0 = – 5 на различных расстояниях: а) z = 0 м, б) z = 0,2 м, в) z = 0,4 м, г) z = 0,6 м, д) z = 0,8 м, е) z = 1,1 м, ж) z = 1,4 м, з) z = 1,7 м, и) z = 2 м, к) продольное распределение интенсивности на интервале z = 0,1...1,9 м

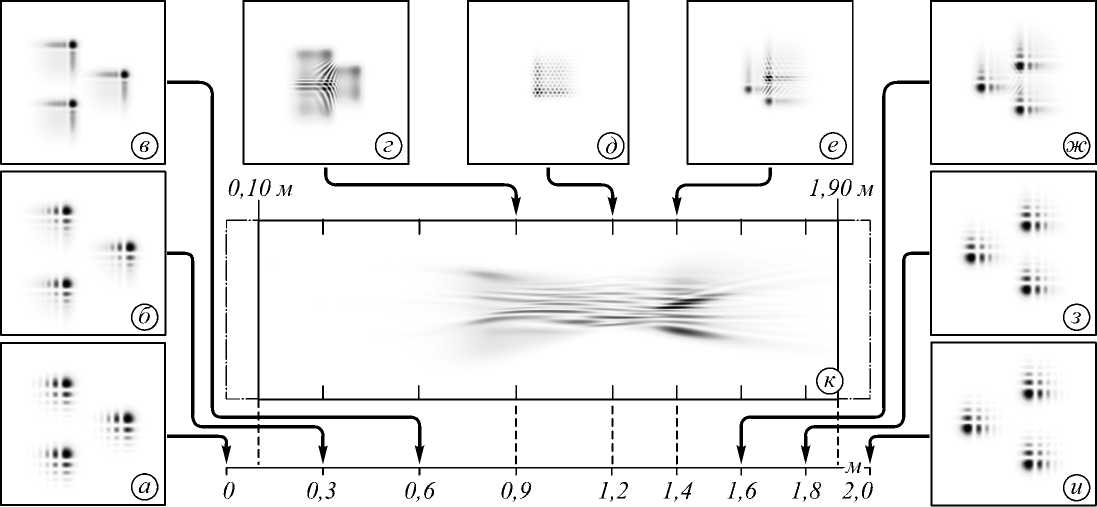
Рис. 6. Распределение интенсивности набора пучков Эйри–Гаусса с параметрами ξ = - 6, α = β = 5, α 0 = β 0 = – 5 на различных расстояниях: а) z = 0 м, б) z = 0,3 м, в) z = 0,6 м, г) z = 0,9 м, д) z = 1,2 м, е) z = 1,4 м, ж) z = 1,6 м, з) z = 1,8 м, и) z = 2 м, к) продольное распределение интенсивности на интервале z = 0,1...1,9 м

Теперь будем поворачивать кластер пучков Эйри– Гаусса на 45 (рис. 7), 90, 135 и 180 градусов (рис. 8) против часовой стрелки (пр.ч.с.).

На рис. 7 и 8 видно, что поворот кластера мод не вносит каких-либо изменений в её траекторию (на рис. 8а – в показано несколько сечений одного и того же кластера под различным наклоном).

Наконец, будем теперь сначала поворачивать каждый пучок Эйри на 45 (рис. 9), 90, 135, 180 градусов (рис. 10), а затем формировать из них набор мод.

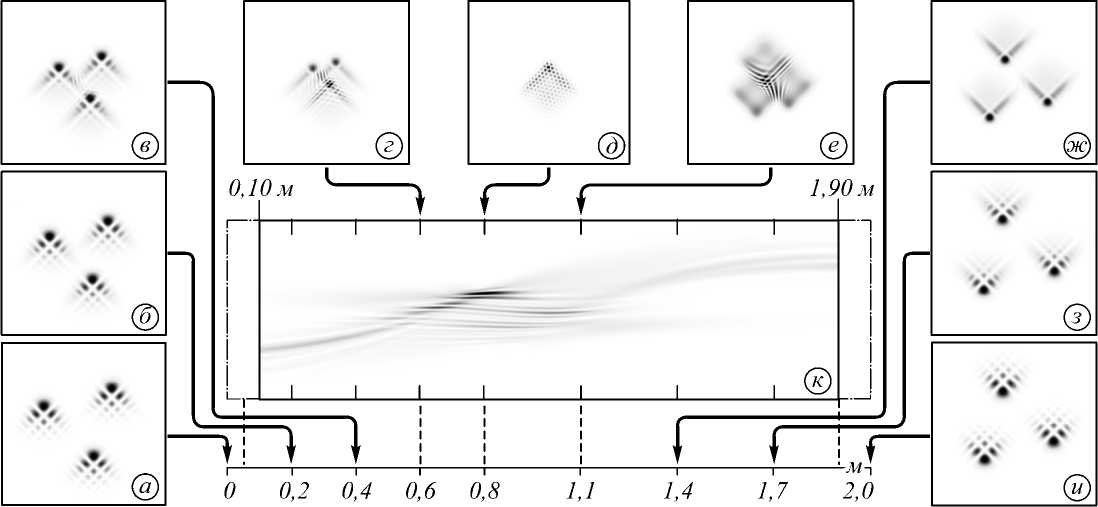
Рис. 7. Распределение интенсивности повёрнутого на 45° пр.ч.с. набора пучков Эйри–Гаусса с параметрами ξ = 6, α = β = 5, α 0 = β 0 = – 5 на различных расстояниях: (а)‐(и) расстояния, как на рис. 5, (к) продольное распределение интенсивности на интервале, как на рис. 5

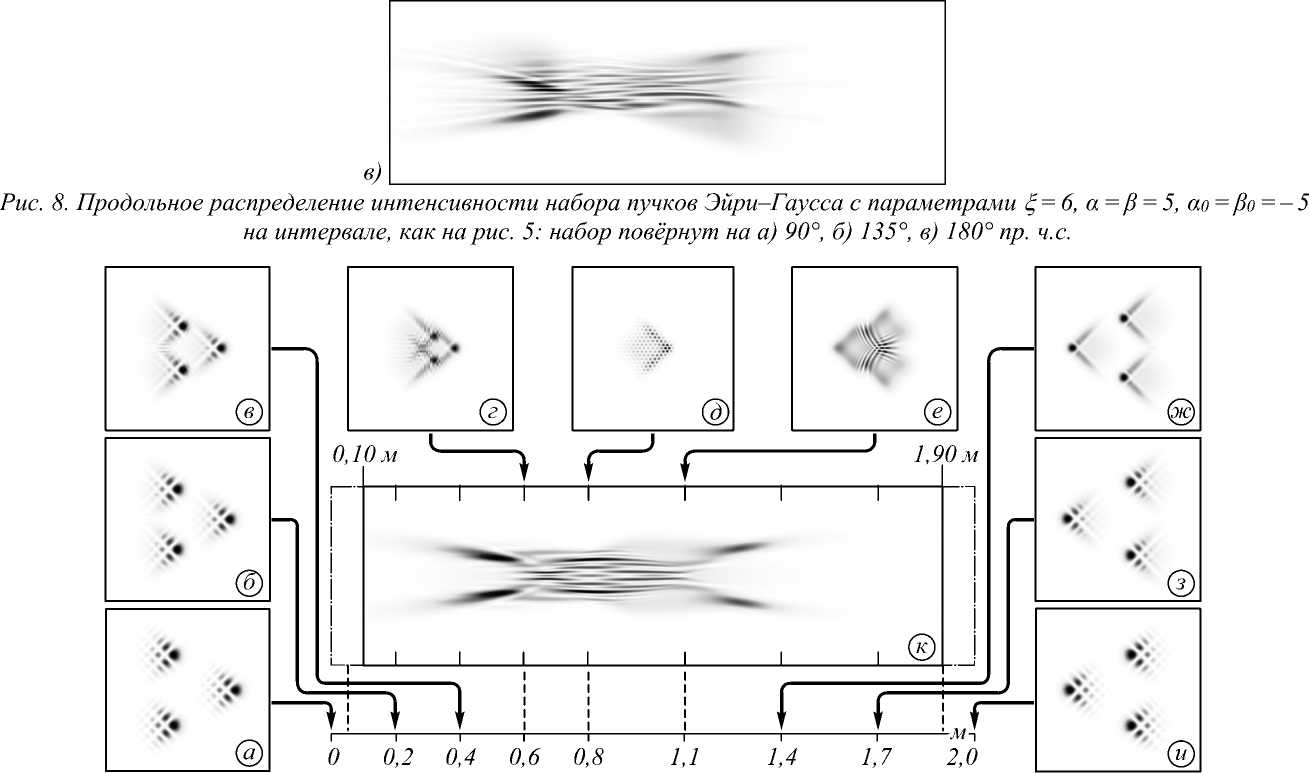
Рис. 9. Распределение интенсивности набора пучков Эйри–Гаусса, повёрнутых на 45° по ч.с. с параметрами ξ = 6, α = β = 5, α 0 = β 0 = – 5 на различных расстояниях: (а)–(и) расстояния, как на рис. 5, (к) продольное распределение интенсивности на интервале, как на рис. 5

а)

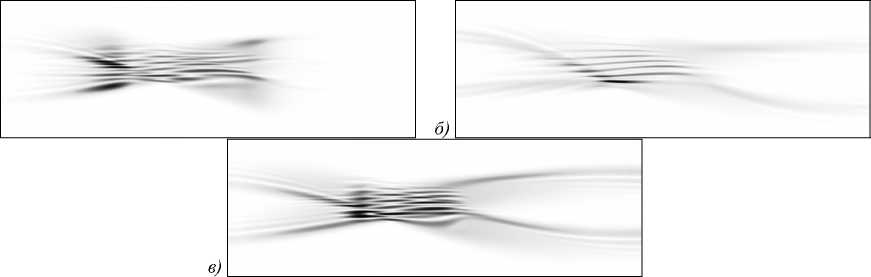
Рис. 10. Продольное распределение интенсивности набора пучков Эйри–Гаусса с параметрами ξ = 6, α = β = 5, α 0 = β 0 = – 5 на интервале, как на рис. 5: пучки повёрнуты на а) 90°, б) 135°, в) 180° по ч.с.

На рис. 9 и 10 видно, что траектория повёрнутых пучков стала более синхронной, но распределение интенсивности в области фокуса и само расстояние фокусировки не изменились.

Заключение

В данной работе исследована возможность изменения траектории распространения набора пучков, смещённых в исходной плоскости, за счёт добавления фазы, имеющей линейную зависимость (аналогично действию призмы). Такой подход применён к модам, обладающим свойством автофокусировки, а именно, к пучкам Эйри–Гаусса, с целью расширения возможности управления свойствами их распространения при автофокусировке.

С использованием дробного преобразования Фурье выполнено численное моделирование распространения таких пучков. Показано, как величина смещения и отклоняющей фазы изменяет траекторию автофокусирующихся пучков Эйри–Гаусса. Результаты показали, что изменение параметра несущей пространственной частоты ξ (аналог параметра призмы) позволяет управлять расстоянием до области фокусировки. При этом форма траектории пучка за счёт наличия линзы в соответствии с теоретическими предсказаниями перестаёт быть параболической. Поворот каждой моды, как и поворот кластера в целом, приводят к ожидаемому в силу бездифракционности пучков Эйри повороту поперечного распределения поля на тот же угол.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант 20-07-00505-А) в части численного моделирования, а также при поддержке Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в теоретической части.