Измерение дальности космического аппарата

Измерение дальности производят на основе последовательного сигнала [2] или с использованием псевдослучайного сигнала [3], а также при передаче дальномерных тоновых синусоидальных сигналов. Методы используют близкие аппаратные решения НКУ и обеспечивают примерно одинаковые результаты [4]. Однако имеются существенные различия [2]. Другие методы измерения дальности КА, основанные на радиолокационных принципах, включая лазерную локацию, здесь не рассматриваются.

Принимаемый сигнал в НКУ подвергается понижению частоты, усилению и демодуляции. Затем оценивается двухсторонняя задержка между переданным и полученным модулирующими сигналами и двухстороннее доплеровское смещение несущей частоты [5; 6].

1.    Структура последовательного дальномерного сигнала

Международный консультативный комитет по космическим данным The Consultative

Committee for Space Data Systems (CCSDS) [4] предлагает дальномерный сигнал в виде последовательности периодических сигналов, когерентно связанных друг с другом, который должен быть связан с несущей частотой линии вверх [2]. В табл. 1 приведены значения диапазонов частот спутниковой связи, согласованных мировым сообществом производителей КА и приемной аппаратуры земных потребителей. В пределах диапазона частот выделяют пользовательские участки, в том числе для исходящей и входящей радиолиний КИС КА. Основную часть дальномерных сигналов представляют т.н. компоненты дальности, имеющие индивидуальный номер. Большой номер представляет собой компонент с меньшей частотой (но большим периодом). Частота fn компонента с номером n относится к несущей частоте uplink для диапазона S в соответствии со следующими выражениями для диапазона S :

fn = 2^- n • f 0 = 2^-( n ⁺⁷⁾ f              (1)

и для диапазона X fn = 2-n ■ f0 = 2

- ( n + 7)

221 _f

749 ^fx

Здесь f_s или f_x – номиналы рабочих несущих частот КИС для диапазонов S и, соответственно, X . Значение частоты уменьшается в два раза относительно предыдущего компонента.

Таблица 1

Условное обозначение диапазона	Полоса частот, ГГц
L	1,452–1,550 и 1,61–1,710
S	1,93–2,70
C	3,4–5,250 и 5,725–7,075
X	7,25–8,40
Ku	10,70–12,75 и 12,75–14,80
Ka	15,4–26,5 и 27,0–30,2
K	84,0–86,0

Компонентам, которые используются в измерении дальности, присвоены номера от 4 до 24, и упорядочиваются они в соответствии с этими номерами. Необходимость использования большого количества компонент объясняется следующим. Когда для измерения задержки сигнала используется периодический сигнал, то появляется т.н. проблема (задача) неоднозначности измерения. Полная задержка содержит, в принципе, целое число

Т 1	Т 2	Т 2	Т 2	Т 2	Т 2	Т 1
С4	С5	С6	С7	С8	С9	С4

Рис. 1. Фрагмент дальномерного сигнала циклов измерительного сигнала плюс некоторая доля цикла. Эта задача в полной мере присуща использованию тоновых сигналов и подробно исследована ниже. Низкочастотные компоненты обеспечивают однозначность измерения задержки, а высокочастотные - точность измерений.

Фрагмент структуры дальномерного сигнала в общем виде приведен на рис. 1. Первым следует компонент, выбранный в качестве синхронизирующего; он излучается в течение T ₁ = 6 c на частоте примерно 1 МГц. В примере это компонент С4. Затем следуют компоненты с понижением частоты и нарастающим на 1 номером до компонента, обеспечивающего необходимое однозначное измерение дальности с наиболее низкой частотой. В примере это компонент С9. Каждый из этих компонентов передаётся за время T ₂ = 3 с. Кроме того, между компонентами предусмотрена пауза длительностью 1 c для успешной перестройки частоты генератора f_n . При периодическом повторении излучения дальномерного сигнала между последним компонентом и синхрокомпонентом следующего дальномерного сигнала предусмотрена удвоенная пауза.

Итак, длительность дальномерного сигнала T _ДС при использовании низкочастотного компонента с номером n _max и синхрокомпонента с номером 4 (в сек.):

T дс = Т 1 + 3 С + ( n max — 5)( T 2 + 1 С ). (3)

Так, для обеспечения однозначного измерения дальности в пределах до 38 тыс. км с точностью порядка 140 м следует использовать компонент n _max = 22, что соответствует частоте f max = ^3,9 ГЦ.

Как указано выше, компонент синхронизации передается за T ₁ секунд, а каждый из следующих тонов передается за Т ₂ секунд, Т ₁ больше Т ₂, поэтому требуется больше времени для корреляции компонента синхронизации, чем для каждого последующего. Эта процедура необходима в процессе обнаружения дальномерного сигнала.

Достоинством измерения дальности с помощью последовательного сигнала явля-

ИССЛЕДОВАНИЯ

Havko-

ЖГРАДА

ется то, что возможно использовать простой коррелятор, который ищет только тон частотной синхронизации. Недостатком этого метода является то, что запуск коррелятора следует производить в момент появления дальномерного сигнала на приемном конце радиолинии, так как должны правильно пройти последовательно все тоны; если работа коррелятора начинается в произвольный момент, то измерение будет испорчено по некоторым тонам.

Метод на основе последовательности компонент сыграл определенную позитивную роль на ранних этапах теоретического и практического развития сферы дальномерных измерений КА. Основной особенностью последовательной дальнометрии является значительная длительность дальномерного сигнала, вплоть до нескольких десятков минут. Это вызвано паузами между компонентами, а также необходимостью излучения достаточно низких частот. Кроме того, должен быть известен момент старта дальномерного сигнала, поскольку это необходимо для правильной последовательной перестройки тонов. Если подобная синхронизация отсутствует, то весьма вероятно, что каждое измерение будет повреждено. В целом это привело к необходимости поиска альтернативных путей, поскольку такое измерение обеспечивает интегральную оценку дальности за счет движения КА. Одно из перспективных направлений состоит в использовании априорной информации о значении дальности на предыдущем такте измерений. Этот подход рассмотрен ниже.

Ниже также рассматриваются методы измерения на основе псевдослучайных последовательностей и на основе фазовых измерений.

2.    Измерение дальности КА на основе псевдослучайной последовательности

Дальномерный сигнал, рассмотренный выше, представляет собой последовательность синусоидальных или прямоугольных сигналов с частотами, которые периодически уменьшаются от стартового значения около 1 МГц до минимального значения в несколько Гц. Измерения сопровождаются погрешностью измерений, которые являются случайными в зависимости от мощности шума, пропорциональной периоду наивысшей частоты тона (т.е. ширине полосы занимаемых частот) и обратно пропорциональной квадратному корню из произведения сигнал/шум (С/Ш) и времени интегрирования, используемого при корреляционной обработке в приемнике.

Измерение дальности с использованием псевдослучайной последовательности ПСП (или псевдошумовой последовательности PN) состоит в формировании и излучении последовательности из компонент длиной 2, 7, 11, 15, 19 и 23 бит. Длительность результирующей PN составляет 1 009 470 бит. Чипы (биты) имеют равную длительность порядка 1 мкс, поэтому длительность дальномерного сигнала не превышает порядка единицы секунд. Рис. 2 иллюстрирует состав PN-последовательности. Биты первого компонента C1 используются для синхронизации по частоте бортового генератора КА относительно частоты опорного генератора НКУ. После битов синхронизации следует собственно PN-последовательность с периодом L. Автокорреляционная функция такой последовательности имеет максимальное значение +L . Остальные пиковые значения АКФ равны -1. Длительность бита обозначена T _C. f_RC = 1/2 T _C, Гц. Символ «С» в обозначении T C образован от сокращения термина Chip, синонима в данном контексте термину «бит». Спектр PN-последовательности достаточно широкий, а после ее свертки на выходе коррелятора ширина информационного спектра оказывается достаточно узкой для обеспечения требуемого отношения сигнал/шум.

Бортовой приемопередатчик синхронизируется под высокоскоростной сигнал PN-последовательности, модулирующий несущую частоту нисходящей линии связи. ФНЧ в составе регенератора обеспечивает ширину

C1 :+1;-1

C2 :+1;+1;+1;-1;-1;+1;-1

C3 :+1;+1;+1;-1;-1;¡1;+1;-1;+1;+1;-1

C4 :+1;+1;+1;+1;-1;-1;-1;+1;-1;-1;+1;+1;-1;+1;-1

C5 :+1;+1;+1;+1;-1;+1;-1;+1;-1;-1;-1;-1;+1;+1;-1;+1;+1;-1;-1

C6 :+1;+1;+1;+1;+1;-1;+1;-1;+1;+1;-1;-1;+1;+1;-1;-1;+1;-1;+1;-1;-1;-1;-1

полосы около 1 МГц. Процедура обработки на приемном конце требует параллельной работы 6 корреляторов, что усложняет аппаратную реализацию. Преимущество этого способа обнаружения дальномерного сигнала на приемном конце радиолинии состоит в том, что снимается ограничение на знание момента появления сигнала.

В направлении вверх с НКУ на КА излучается опорная последовательность, которую также называют зондирующим сигналом. Принимаемый дальномерный сигнал усиливается и ограничивается по двум порогам – в областях положительных и отрицательных напряжений, например, с помощью триггера Шмитта, с целью получения последовательности вида ±1 для дальнейшего вычисления корреляции между принимаемой последовательностью и зондирующим сигналом.

Корреляция (перемножение принятого и опорного чипов с последующим суммированием) принятой дальномерной последовательности производится каждой опорной последовательностью и ее отдельных циклических сдвигов. Это позволяет определить, какой циклический сдвиг наиболее близок части полученной последовательности. Когда принятая последовательность максимально совпадает с задерживаемой по тактам опорной последовательностью, это позволяет определить задержку (по модулю дальномерной последовательности периода L ) в чипах, т.е. время прохождения сигналом двойного пути. Одним из важных показателей качества зондирующего сигнала является время обнаружения, под которым понимается время, необходимое для выполнения корреляции с учетом всех циклических сдвигов зондирующего сигнала. По понятным причинам это время должно быть как можно меньше.

Первой задачей приемника (после демодуляции принятого фазомодулированного сигнала) является поиск составляющей сигнала для синхронизации. Джиттер (флуктуации) сигнала синхронизации из-за теплового шума антенны и высокочастотного тракта определяет стандартное отклонение ошибки измерения в метрах, т.е. дисперсию случайной составляющей результата измерения дальности.

3.    Измерение дальности КА на основе фазовых измерений

Расстояние между НКУ и КА можно оценить на основе измерения разности фаз излученного с НКУ и приема переизлучен-ного транспондером КА гармонического сигнала. Кроме того, следует иметь в виду, что PN-последовательность прямоугольных импульсов с выхода демодулятора на приемном конце радиолинии подвергается фильтрации так, что высокочастотные составляющие значительно уменьшаются и сигнал превращается в синусоидальную последовательность тактовой частоты, со сменой фазы в пределах ±180° соответственно значениям ±1 бит ПСП. При этом нужно помнить, что только 81 % мощности прямоугольных сигналов зависит от основной, или первой, компоненты (гармонической составляющей). Это уменьшает отношение сигнал/шум относительно значения с выхода демодулятора приемника.

Полная фаза задержки сигнала на трассе НКУ-КА-НКУ определяется двойным временем распространения сигнала 2Δ t (без учета задержки в транспондере):

2 R

V = 2А tto = 2п---f = 2л- c

Здесь R - расстояние между НКУ и КА (дальность КА); ю - несущая частота непрерывного сигнала, фазовая задержка которого измеряется; c – скорость света; λ – длина волны. Обычно фазометр имеет пределы измерения φ_из = (0...2π), поэтому (11) можно записать в виде

ψ = 2π z + φ из . (5)

Здесь z – число целых циклов фазы на трассе НКУ-КА, z = R /X; ф_из - дробная часть полной фазы ψ по модулю 2π, результат измерения фазометром [8]. Поскольку сигнал проходит двойное расстояние, то дистанция между НКУ и КА определяется по формуле

(о 1

R =± z . ^Пи .

2 у    2 п J

Здесь z = 0, 1, …, φ из ≤ 2π. Это порождает т.н. задачу о разрешении многозначности фазовых измерений [2], которая иллюстрируется рис. 3, где дальность R выражена в единицах длины волны λ в подрисуночной строке «вч». Если, допустим, результат измерения по вч φ_{из вч} = π, то это значение возможно при дальностях Ri = i λ вч /4, i = 1, 3, 5, 7. Одним из решений этой задачи является использова-

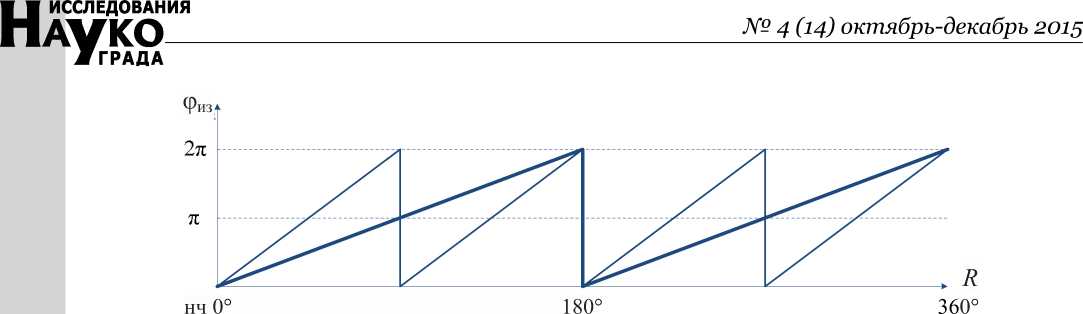
вч 0°               180° (λ/2)         360° (λ)             180° (3λ/2)       360° (2λ)

Рис. 3. Зависимость φ_из( R ) для двух частот

ние модулированного по одно тров сигнала необходимой ча основе многочастотного мето щего многошкальный принцип измерения. Стандарт ESA предусматривает разрешение многозначности многошкальным методом с использованием нескольких кратных частот от т.н. мажорного тона (основной частоты) до минорных, более низкочастотных тонов [7]. Частота мажорного тона равна 100 кГц; частота минорных тонов уменьшается в геометрической прогрессии с коэффициентом 1/5 по отношению к основному тону (20 000 Гц, 4 000 Гц, 800 Гц, 160 Гц, 32 Гц, 8 Гц); а также минорных тонов, получаемых путем смешивания с другими минорными тонами (20 кГц, 16 кГц, 16 800 Гц, 16 160 Гц, 16 032 Гц, 16 008 Гц). Это дает возможность точного измерения расстояния путем измерения сдвига фазы основного тона с неоднозначностью, разрешаемой с помощью минорных тонов; в рассмотренном примере неопределенность не превышает 18 000 км. Передача минорных, особенно низкочастотных, тонов сопряжена с известными трудностями. Смешивание их с другими тонами позволяет поднять частоты минорных тонов, так что их можно передавать по радиолинии КА - НКУ без особых затруднений. Высокочастотный тон определяет точность дальнометрии. Низкочастотный тон обеспечивает разрешение неоднозначности фазовых измерений. Сначала дальность КА оценивается с точностью до 1/2 длины волны самого низкочастотного тона, и в последующем значение дальности уточняется в результате последовательной передачи и обработки более высокочастотных тонов. Следствием этого является достаточно длительная процедура определения дальности КА, что ограничивается сверху движением КА на ГСО. В [9] отмечается, что максимальная относительная скорость движения КА, вызванная отклонением орбиты КА от круговой, составляет около 27 м/с. Измерение дальности и времени передачи должно произойти c интервалом не более 10 мс друг от друга, чтобы сохранить ошибку, вызванную из-за изменения дальности КА, приемлемо минимальной. На практике раз ность во времени между измерением дальности и передачей не превышает порядка 1 мс.

Тогда (6) можно записать в следующем виде:

п _ к L +Физт) .^Rv             Z I i 2(i 2nJ

i = 0, 1… . Длина мажорной (грубой, i = 0) волны определяется по (7) исходя из z ₀ = 0 и φ из0 = 2π. Так, для геостационарного КА с высотой орбиты R = 36 000 км и частотой сигнала 100 Гц (длина волны 3 000 км) дистанцию между КА и НКУ покроет примерно z = 24 полуволн. Однозначное измерение расстояния КА – НКУ возможно только при R ≤ λ/2, что требует использования частоты f₀ = 4,17 Гц при z₀ = 0. Понятно, что непосредственное излучение столь низкой частоты невозможно, поскольку нереально создание антенны, эффективно излучающей столь низкие частоты. В табл. 2 приведены значения диапазонов дальности R и соответствующие им диапазоны результатов измерения фазометром φ_из для двух значений длин волн. Как видно, зона неопределенности уменьшается вдвое при двукратном уменьшении длины

Таблица 2

λ, км φиз R 72 000 0 < φиз < π 0 < R < 36 000 км π < φиз < 2π 36 000 < R < 72 000 км 36 000 0 < φиз < π 0 < R < 18 000 км π < φиз < 2π 18 000 < R < 36 000 км волны. Основная погрешность измерения R определяется неточностью фазометра. Пусть, например, Афиз = 1°, что приведет к погрешности измерения на самой низкой, «мажорной» частоте ΔR ≈ 55 км, что явно не удовлетворяет требованиям практики. Поэтому второй причиной повышения частоты дальномерного сигнала является необходимость повышения точности дальномерных измерений.

На рис. 3 приведена также зависимость φ_{из mod 2π} ( R ) по нч. Сопоставление результатов измерения по двум частотам позволяет принципиально решить задачу разрешения неоднозначности. Однако, если φ_{из mod 2π} близко п или 2п по любой частоте, возможна большая погрешность, вызванная шумом, когда отсчет фазы может располагаться слева или справа относительно указанной границы. При использовании усреднения возможна погрешность в 180°. Поэтому необходимо предпринять меры, исключающие такую погрешность. Если результат измерения оказался близок указанным границам, то полезно ввести задержку на 180° на передающем конце для сигнала одной либо обеих частот и учесть это смещение при вычислении истинного значения дальности R .

Очевидно, что использование более высоких частот обеспечивает повышение точности измерения R . Поэтому прибегают к использованию минимум двух или более частот. Разность полных фаз сигналов на частотах f ₁ ^и f > ^по (4)

A^ = V 1 —V 2 = 2 п 2R- ( f 1 - f 2 ) = 4 п R— . (8) cc

С другой стороны

^АУ = ^2п( z | ^- z ₂) ⁺ (фш м ^- 4W)*     ⁽⁹⁾

Для этого случая интервал однозначного определения дальности А R од = С/2Аf Измерение при малой разности частот позволяет расширить интервал неоднозначности. Полезным также является использование априорной информации о дальности КА, находящегося в режиме штатной эксплуатации на ГСО. При выборе значения f или Af следует исходить из условия Rmax - Rmin < X/2, где R max и R min, соответственно, возможные максимальное и минимальное удаления КА от НКУ. Параметр z будет иметь постоянное и изв    е значение для любого положения КА в лах Rmax ^ Rmin. Пусть, например, Rmax - ^mm =

= 400 км при среднем значении R = 36 000 км. Выберем X = 993 км, т.е. f = 302 Гц. Тогда в пределах (72 000 ±400) км параметр z не выйдет за пределы 72, т.е. однозначность измерений будет обеспечена. Измеряемое значение фазы не выйдет за пределы φ_из ≈ (30…330)°.

Движение КА приводит к ошибке, вызванной эффектом Доплера, особенно если производится измерение с усреднением результатов нескольких испытаний. Обычно для борьбы с этим вводят упреждающее смещение измерительной частоты, равное значению доплеровского сдвига с противоположным знаком. Эффективность этого приема обусловлена детерминированностью движения КА на ГСО, что позволяет прогнозировать доплеровский сдвиг частоты.

Из (6) следует, что погрешность дальномерных измерений Δ R является функцией точности измерения фазы Δφ:

A R = Аф изЛ . (10) 2 п 2

Это выражение, в частности, объясняет уменьшение погрешности Δ R с увеличением частоты сигнала.

Оценка фазовой задержки ф_из принятого сигнала г 2 ⁽ t ) = U Tsiⁿ(_m t ^{+ Ф)} относительно переданного сигнала s ₁( t ) = U ₁∙sin ω (рис. 4) производится по формуле

ф =^£. 360°.

из T

Здесь Т - период сигналов г 1 ( t ) и г ₂( t ). Прямоугольные импульсы длительностью A ti называют фазовыми интервалами. Различают однократное измерение по (4) и измерение с усреднением [10]:

Ф из = 3607i E A t i . (11)

^NT i = 1

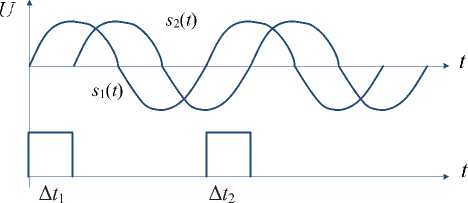
Рис. 4. Формирование фазовых интервалов

Havko-

ЖГРАДА

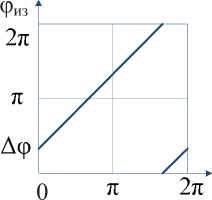
Рис. 5. Фазовая характеристика при смещении уровня привязки

1                да

W ( ф ) = — ¹ + ² Z C i • cos i ( ф^-ф _с) . 2 п

i = 1

Г I¹ + 7 J

Здесь Ц = <   ^{2 }} • qC F i

i !• 2²

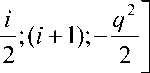
В следующих операциях длительность фазового интервала измеряется цифровым способом.

По принципу формирования фазового интервала фазометры подразделяют на триггерные фазометры и фазометры с перекрытием, которые различаются формой фазовой характеристики. Большое влияние на погрешность измерения триггерным однополупери-одным фазометром оказывает Δ Ui – смещение уровня привязки от нулевого значения в каналах переданного и принятого сигналов, возникающее по разным причинам. Этот параметр приводит к дополнительному неинформативному сдвигу фазы

Г - гамма-функция; F 1 - вырожденная гипергеометрическая функция; ф_с - фаза сигнала. Заметим, что для q = 0 W (ф) = 1/2п, что соответствует равновероятному распределению фазы в пределах 0…2π. С другой стороны, для q > 2 закон распределения фазы близок к нормальному со среднеквадратическим значением

О

ф

^О ш = ¹

U 2 q ’

здесь ^ ш - дисперсия (мощность) шума в составе принимаемого сигнала. Статистические характеристики – математическое ожидание (систематическая погрешность) и дисперсия вычисляются по обычным правилам:

П

^Дф сист = j Ф W ( ф ) d Ф ,

-П

Дф = arcsin

' Д U 1 ^л

< U 1 >

arcsin

Д

V ^U 2 /

Д U 1

U ₁

A U 2

U ₂

₂ ^П _{2                   2}

о Jj ^^(ф)^^ф Д^фсис т .       (14)

(рис. 5).

Заметим, что ,

T

2 ²                2 ^T

Д U, = — [ U • sin to tdt --f U, • sin to tdt.

T I              T T

Отсюда систематическая погрешность

Аф_сист =П { Ф [ q ( п-^d -Дф ) ] +

^{+ Ф} [ q ( п-kd ^+д ф ) ]} .          ⁽¹⁵⁾

Здесь Ф ( x ) – интеграл вероятностей;

Ф ( X ) =

V2n

хx j e 2 dx.

-да

Систематическая погрешность зависит от отношения сигнал/шум и, что не менее важно, от фазы сигнала. Зависимость систематической погрешности от неравенства уровней привязки в каналах можно не учитывать, если обеспечивается отмеченное выше условие Δ U_i = 0, при котором

Дф сист = 2 п Ф [ q (п - |ф с |)]. (16)

При фс ^ п систематическая погрешность определения дальности КА ∆Rсист → λ/4 (в пределах выбранного z). Поэтому для не- допущения больших значений методической систематической погрешности определения дальности КА необходимо принимать соответствующие меры.

Разрывность фазовой характеристики фазометра является причиной погрешности, остро проявляющейся под воздействием шума, когда измеряемый фазовый сдвиг находится в области, прилегающей к разрыву, т.е. к 0°, 360°. Пример: пусть истинный фазовый сдвиг фс = 358°. Под влиянием шума φизм может принять значения, например, 359° или 357°. Погрешность измерения не превысит ±1°. Но если φизм примет значение 1°, то погрешность достигнет 357°. В усредняющих фазометрах, когда производится усреднение нескольких измерений с целью уменьшения погрешности, вызванной шумом, среднее значение при непревышении физм границы разрыва ±180° для другого типа фазометров, получивших название фазометров с перекрытием.

Разрывность характеристики фазометра приводит к появлению особенностей работы в присутствии шума различной интенсивности. Шум на входе измерителя фазы следует считать узкополосным, как прошедший тракт приемника. Случайная составляющая погрешности измерения дальности прямо пропорционально зависит от случайной составляющей измерения фазовой задержки

σ R = σ ϕ _из

λ

⋅

2 π

поскольку остальные параметры известны точно. Очевидно, что уменьшение длины волны (увеличение несущей частоты) повышает точность измерения дальности, но уменьшает диапазон однозначного измерения. Интересно отметить, что Сколник показал, что погрешность дальнометрии можно определить по формуле [1]:

= ^c , ^R  2 π f 2 P c / N 0

которая совпадает с (25), полученной из других соображений; P _с - мощность сигнала.

Когерентный прием сигналов, который обеспечивается с помощью автоподстройки частоты опорного генератора, позволяет производить оценку неизвестной фазы. Однако произвольность начальной фазы может привести к ошибкам. В системах связи это обстоятельство может привести к т.н. обратной

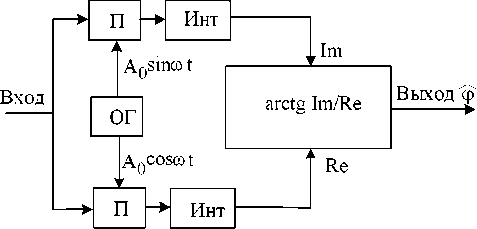
Рис. 6. Квадратурный корреляционный измеритель фазы

работе устройства, когда принятые биты самопроизвольно инвертируются, что недопустимо при дальномерных измерениях. Для решения задачи корреляционного приема сигналов с произвольной начальной фазой широко используют т.н. квадратурную, или ортогональную (или двухканальную ), методику. Такой измерительный приемник (рис. 6) содержит: П - перемножитель, Инт - интегратор, arctg – узел вычисления функции arctg z .

Опорный генератор ОГ формирует опорные сигналы единичной амплитуды синфазного (синусного) канала и квадратурного (косинусного) канала . Пусть принимается сигнал единичной амплитуды 5 1 ( t ) = А ^ш(ш t + ф), 0 < t < T , где ф - начальная фаза, принимающая произвольное значение в результате прохождения сигнала по трассе и значение которой необходимо измерить; Т – длительность сигнала. Результаты интегрирования в каналах:

T                     AA T

Re = j A • srn( ro t + ф ) • cos ro tdt =        sin ф , (19)

T                     AA T

Im = J A • siⁿ⁽ ro t + ф ) • sin ro tdt = cos ф ⁽²⁰⁾

при ro T = 2n n , n - целое; А _о - амплитуда опорного сигнала. Тогда оценка фазы

Im ф = arctg   .

Re

Функция arctg определена на интервале ±п/2, поэтому при вычислении значения неизвестной фазы по (21) необходимо учитывать знаки числителя и знаменателя для переноса результата в соответствующий квадрант. Оценка по (21) обеспечивает максимум функционала правдоподобия, т.е. является максимально правдоподобной . Поэтому фазометр, реализующий алгоритм (21), обеспечит ми-