Измерение диаметров цилиндров методом обработки изображений

Дистанционные измерения геометрических размеров изделий машиностроения с помощью электромагнитных волн оптического диапазона делятся на когерентные (дифракционные, интерференционные, спеклструктуры) и некогерентные; с построением изображения или без построения; с фильтрацией на оптических частотах или после преобразования в электрический сигнал. Когерентные оптические системы являются наиболее универсальными и позволяют производить параллельную обработку двумерных полей со скоростью распространения света, но высокие требования к качеству элементной базы и среды распространения связывают применение когерентных схем с развитием интегральной оптики. Поэтому более широко в производственных условиях используются некогерентные по принципу действия установки, хотя источником света в них может служить и лазер, особенно там, где необходима спектральная селекция, высокие пиковые мощности, малая расходимость пучка. К числу основных потребителей оптикоэлектронных, в том числе и лазерных, измерительных приборов относятся производства со 100 %-ным выходным контролем [1], т.е. авиастроительные фирмы и изготовители аэрокосмической техники.

В последнее время происходят существенные изменения в характере контроля линейных размеров в машиностроении - переход от ручных, визуальных методов к автоматизированным и дистанционным. Автоматизированные измерения обеспечивают объективность контроля, высокие точность и производительность дают возможность оперативно изменять ход технологического процесса, снижая или вовсе исключая брак по причине выхода геометрических размеров за допуски к оптико-электронным системам для промышленного применения предъявляются следующие требования: быстрый вывод результатов на монитор, надежность функционирования в неблагоприятных условиях, соответствие принятым стандартам, контроль аппаратных и программных ошибок [2].

Измерение диаметра детали цилиндрической формы и его приращения одна из наиболее распространенных контролирующих процедур, для реализации которой методами обработки изображений был предложен следующий алгоритм [3]. Суть алгоритма поясняется рис.1. На изображении цилиндра периодически измеряются ординаты точек пересечения границ цилиндра с двумя, расположенными на расстоянии / друг от друга вертикалями х,= constj и %2 = const2 Ур У2, У), у4. Для каждого кадра вычисляется диаметр:

d = <Уг ~ Уз) cosarctg       ;                                    (О ордината центра изображения цилиндра:

^+У2+Уз + У4

У.=—"---- ;                      (2)

и его наклон:

a = arc(gti

и поле зрения телекамеры. Предложенный алгоритм интересен тем, что диаметр и наклон цилиндра вычисляются как разности соответствующих координат, и, следовательно, результаты его работы инвариантны к смещениям и поворотам цилиндра в поле зрения.

Рис.1. Схема измерений. Вид изображения цилиндра в поле зрения прибора.

Приращение диаметра определяется как разность следующих друг за другом измерений:

д^ = ^1"<- (4)

Если это приращение есть следствие обработки по образующей вращающейся детали (точение на токарном станке, наплавка, напыление и т.п.), то за толщину напыляемого покрытия можно принять половину приращения.

Чтобы реализовать алгоритм измерения диаметра или его приращения, необходимо выделить изображение цилиндра из фона и определить точные положения его границ. Вначале осуществляется приближенное выделение границ методом наибольшего градиента. Для этого вычисляются суммарные освещенности каждой строки £/ _£, а также значения разностей освещенностей dE_lL=E_x+1 е'-^е- Положения строк с минимальным и максимальным значениями разности’ определяют приблизительное местоположение границ цилиндра. В результате все поле зрения разделяется на три области: две области -фон и одна - цилиндр, вычисляются средние освещенности фона Е_ь и цилиндра Е_е и назначаются пороговые уровни обработки. Некоторая точка изображения А(х,у) относится к области фона S_b или цилиндра 5₀, если:

Sb, Ел^р(Еь+Ес)

А(х,у) е

Ел <Р(Еь^ЕЛ где Ед - освещенность изображения в точке А; р - порог.

Определение точного положения координат границ цилиндра и точек других его характеристик включает следующие этапы:

• -    пороговую обработку;

• -    достижение разрешения менее размеров одного пиксела изображения;

• -    исключение систематических ошибок, обусловленных аберрациями;

• -    вычисление коэффициентов уравнений прямых, аппроксимирующих верхнюю и нижнюю границы изображения цилиндра;

• -    вычисление ординат точек пересечения границ с вертикалями Xy=constj и Xj—const2 и характеристик цилиндра (см. (1)...(4)).

Пороговая обработка проводится по каждому столбцу изображения. С целью повышения помехоустойчивости процедуры выделения координат границ изображения Цилиндра к точечным дефектам оптического тракта и ПЗС-матрицы окончательное решение об отнесении точки к изображению цилиндра или фона принимается, если 10 последующих точек также принадлежат той же области по условию (5). Это, естественно, ограничивает динамический диапазон измеряемых значений диаметров снизу 10

пикселами изображения и допустимые наклоны цилиндра в поле зрения телекамеры сверху.

Жесткий растр твердотельных ПЗС-матриц выгодно отличает их от электровакуумных двумерных преобразователей (видиконов, суперортикопов и т.п.). Размеры одной ячейки ПЗС-матриц серийного производства колеблются от 8 до 30 мкм [4, 5]. Многофазная структура каждого элемента и тот факт, что фотогенерированные заряды можно накапливать под произвольно выбранным электродом элемента с многофазной структурой, позволяет фиксировать положение фрагмента изображения с точностью до долей размера фоточувствительной ячейки. Эта доля обратно пропорциональна удвоенному значению числа фаз элемента [6].

Для ПЗС-телекамеры КТМ-1 с матрицей К1200ЦМ7, размер элемента которой 18x19 мкм, а число фаз управления 3, разрешение, достигнутое оптимизированной процедурой считывания зарядовых пакетов, составит 3 мкм. Однако, во-первых, здесь потребуется на одно измерение обрабатывать не один, а три кадра изображения при фиксации измеряемого объекта относительно телекамеры. Во-вторых, подвергается перестройке схемотехническое решение телекамеры.

Улучшить разрешение в определении координат границ цилиндра возможно программными средствами, используя алгоритм, предложенный в работе [7]. Он заключается в аппроксимации величины освещенности в области границы цилиндра прямой линией, но авторы привели лишь качественные аргументы и экспериментальные результаты в пользу выбранной аппроксимации и ее реализации.

Теоретическое обоснование этого алгоритма состоит в следующем. Пусть кадр содержит изображение темного цилиндра на светлом фоне. Вследствие аберраций или преднамеренной дефокусировки изображение границы будет размыто и займет несколько пикселов матричного фотоприемника в направлении, перпендикулярном линии границы, причем вблизи границы зависимость освещенности изображения от ординаты линейна (рис.1):

Е = ту + с,                                          (6)

где т и с постоянные коэффициенты, которые вычисляются методом наименьших квадратов по небольшому (3...7) числу отсчетов [7].

Для упрощения расчетов предположим, что при переходе от цилиндра к фону освещенность изменяется от Е_ь=0 до £^=1. Истинное положение границы у₀ в этом случае будет соответствовать уровню Eq=0,5. Если граница растягивается на п пиксел, то /=1 будет соответствовать Е_х=0, a i=n Е=1.

Тогда т = ~                            (7)

п-1

и

Ей-с

У_й=^—-                             (8)

гп

Погрешность измерения ординаты границы Ду0 находим дифференцированием выражения (8):

Д£ +Дс Дт

Ьуй =------+—г(£0" с), т т где д£, Дс и Дт - абсолютные погрешности соответсвующих величин г. При проведении анализа погрешностей координатных измерений предположим, что прямая (6) проходит через начало координат, т.е. с=0. После чего подставив £о=О,5 и (7) в (9), получим:

ДЕ +Дс     Дт

(Ю)

Ау₀=-----+0,5— т     т

Статистические погрешности определения коэффициентов прямой т и с при равновзвешенной точности измерений освещенности как по координатам, так и по уровням a^const приведены в работе [8]:

Дс = ог

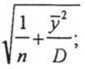
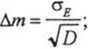
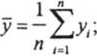
(И)

D^Y^-ny1 ;

п= 3,5,7,...,2М,

где п интерпретируется как число пиксел, на которое растянуто изображение границы. Из условия с=0 следует, что

У1=0, У2⁼¹> Уз⁼²>— ^=<-1.                          ⁽¹⁶⁾

Кроме того, примем а^ЕЕ. В результате получается удобное для расчетов и анализа выражение

1 У¹

1 + J-+—+0,5(л-1) Д£"(п-1) .

п

D

Как видно из (17), между Ду и ЕЕ существует прямая пропорциональная зависимость, т.е. путем уменьшения погрешностей измерения освещенности можно добиться точного определения положения границы. С другой стороны, увеличение числа отсчетов, используемых для построения прямой методом наименьших квадратов, наоборот, вызывает увеличение погрешности Ду.

Численные расчеты потенциальной точности измерения положения границ выполнены с помощью выражений (13)...(17) для практически важных случаев, когда линейный закон изменения освещенности на изображении границы цилиндра соблюдается на расстоянии /1=3,5,...,15 пиксел, а фотоприемник различает 1,2,4,..., 128 градаций освещенности, т.е. для Д^=1/2, 1/4,..., 1/256. Результаты расчетов приведены на рис.2. Все поле графика пунктирной горизонталью разделено на две области по уровню Ду₀ =0,5. Интерес представляет область, заключенная между осью ЕЕ и пунктирной линией. Внутри этой области применение аппроксимирующего алгоритма дает выигрыш в разрешении по координате и потому имеет смысл. Малая разориентация границы цилиндра относительно ПЗС-матрицы не сказывается на точности отсчетов [9].

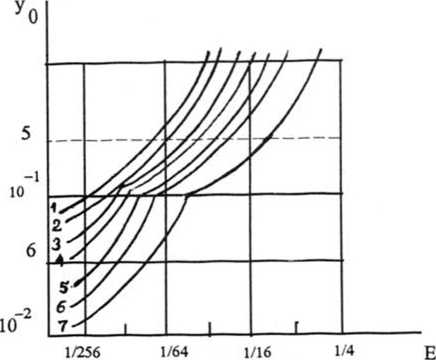
1/128        1/32        1/8

Рис.2. Погрешность измерения ординаты границы цилиндра: Ду - погрешность измерения в пикселах; ДЕ - разрешение телекамеры по освещенности в относительных единицах: 1-и=15, 2-л=13, 3-и=11, 4-и=9, 5-и=7, 6-л=5, 7-л=3.

Описанный алгоритм повышения пространственной разрешающей способности реализуется тем, что пороговая обработка проводится по крайней мере 3 раза. Положение границ цилиндра в каждом столбце изображения определяется по порогам д (г=3,5,...,2£-1). Затем в каждом столбце рассчитывается точная ордината границы с помощью выражения (8).

Систематические ошибки в определении координат, обусловленные аберрациями исключаются с помощью табличной коррекции, суть которой состоит в использовании предварительно полученных данных по контрольным образцам [7]. Таким образом, по каждому кадру изображения формируются два массива ординат для верхней и нижней границ цилиндра. Коэффициенты уравнений границ, которые предлагаются прямыми, рассчитываются также методом наименьших квадратов, используя данные, содержащиеся в массивах.

На заключительном этапе вычисляются ординаты точек пересечения границ с вертикалями x1=const1 и X2=const2 и другие характеристики цилиндра (1)...(4).

Измеритель диаметров состоит из комплекса приборов: ПЗС-телекамеры КТМ-1, устройства ввода-вывода изображений, ПЭВМ, блоков питания. Структура прибора представлена на рис.З. Устройство ввода-вывода изображений предназначено для ввода, хранения и вывода изображений, представленных стандартным телевизионным сигналом. Основные его характеристики следующие: внутренний формат изображения 256x256x8 бит, число градаций серого при выводе изображения 256, число градаций серого при вводе изображения 64; время одного кадра изображения 20 мс, интерфейс - шина типа Q-BUS. Все детали устройства ввода-вывода смонтированы на одной плате, которая занимает одно свободное плато-место в корзине ПЭВМ.

Экспериментальные оценки технических характеристик прибора проводились на оптическом стенде с использованием контрольных образцов. Контрольные образцы представляли собой металлические цилиндры со шлифованной и аннодированной поверхностью. Геометрические параметры эталонных образцов контролировались на измерительном двухкоординатном приборе ДИП-1 проекционным методом с погрешностью ±4 мкм. Конусность и эллипсность образцов не выходили за пределы допустимой погрешности прибора ДИП-1, а диаметры имели значение: 2,173 мм, 6,856 мм, 8,673 мм, 13,671 мм.

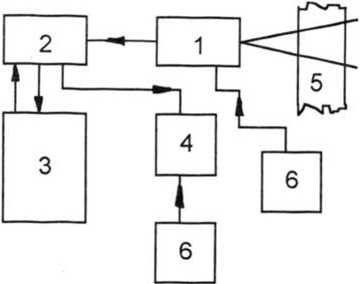
Рис.З. Функциональная схема измерителя диаметров

• 1    - ПЗС-телекамера КТМ-1; 2 - устройство ввода-вывода изображений; 3 - ПЭВМ;

• 4    -графический монитор; 5 - измеряемый цилиндр; 6 - блок питания.

Экспериментально исследовались зависимости измеренного прибором диаметра контрольного образца от его поступательного смещения, угла поворота, контраста и порога, а также повторяемость результатов. Эти зависимости представлены на рис.4-рис.6, соответственно. Контраст освещенности К изображения фона и цилиндра рассчитывался стандартно с помощью выражения:

^ = ^А                        (18)

ЕЬ*ЕС

Как видно из рис.4, поступательное смещение образца, поперечный размер которого занимает ~30 % поля зрения, вызывает разброс измеренных значений диаметра не более 1%. Для тонкого контрольного образца £>=2,173 мм этот разброс не превышает 5%. Тем не менее последнее обстоятельство указывает на необходимость согласования оптического увеличения с характеристиками объекта измерения в заданном интервале величины диаметров. Поворот образца в поле зрения на угол -10° < а < 10° также дает разброс измеренных значений диаметра не более 1% (см,рис.5). Изменение контраста в пределах

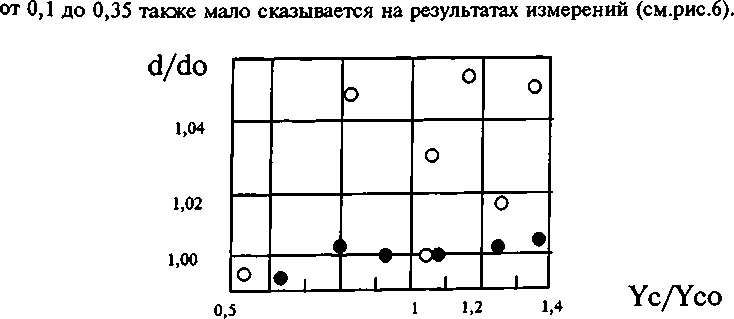
Рис.4. Зависимость измеренного значения диаметра от поступательного смещения образца в предметной плоскости d - измеренное значение диаметра при произвольной координате центра цилиндра в поле зрения прибора ус; d0 - измеренное значение диаметра.

когда образец находится в центре поля зрения у^.

о - диаметр контрольного образца 2,173 мм;

е - диаметр контрольного образца 13,671 мм.

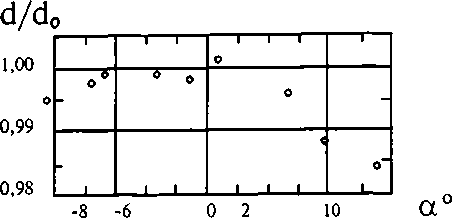
Рис.5. Зависимость измеренного значения диаметра от поворота образца

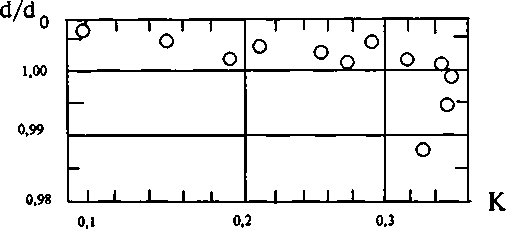
Рис.6. Зависимость измеренного значения диаметра от контраста