Измерение длины волны источников излучения эллипсометрическим методом

ВВЕДЕНИЕ                       ОПИСАНИЕ МЕТОДИКИ

Во многих прецизионных приборах используется монохроматический или квазимонохромати-ческий источник со стабильным спектром излучения. Иногда возникает необходимость контроля этой стабильности. Например, длина волны светоизлучающих диодов (СД) при изменении температуры окружающей среды ощутимо изменяется [1]. Провести же калибровку СД, как правило, означает поставить довольно сложный эксперимент, в котором необходимо поддерживать температуру СД постоянной в течение длительного времени. Такой эксперимент можно осуществить с помощью хорошо разработанного спектрофотометрического метода.

В настоящем сообщении предлагается принципиально новая и более простая методика измерения длины волны монохроматического излучения, позволяющая обнаружить изменения длины волны вплоть до 10–3 нм. Хорошо известно, что сдвиг фазы между двумя ортогональными составляющими вектора электрического поля, приобретаемый при прохождении через анизотропную пластинку, зависит от длины волны светового излучения. При известных параметрах фазосдвигающей пластинки можно решать обратную задачу, т. е. определять длину волны светового излучения. Такая методика легко реализуется на серийно выпускаемых эллипсометрических приборах. В настоящее время разработаны миниатюрные эллипсометры [2]. Это обстоятельство делает предложенную методику еще более привлекательной для контроля длины волны излучения монохроматических светоизлучающих приборов.

Вначале рассмотрим эксперимент по калибровке СД, осуществляемый с помощью спектрофотометрической установки. На рис. 1, а, представлена зависимость спектра излучения СД от температуры. Эта зависимость измерена на спектрофотометрической установке, основа которой — двойной монохроматор СДЛ-1. При этом в монохроматоре использовались две дифракционные решетки с 600 штрихами на миллиметр. Обратная линейная дисперсия монохроматора с такими решетками составляет 1.6 нм/мм, что при выходной щели 0.05 мм соответствует разрешению 0.08 нм. Излучение регистрировалось фотоприемным устройством типа ФЭУ-79 в режиме счета одиночных фотонов. Сканирование проводилось в диапазоне от 630 нм до 700 нм с шагом 0.1 нм. Все спектры нормировались на спектральную чувствительность прибора, полученную на основе известного спектра эталонной лампы. Шкала длин волн спектрофотометра калибровалась по линиям аргонового лазера. Из спектров на рис. 1, а, видно смещение положения максимума в красную область при повышении температуры. На рис. 1, б, приведена зависимость положения максимума в спектре излучения СД ( λ А ) от температуры. При этом эта зависимость хорошо описывается линейной функцией: X A = Л 0 + C ■ t , где X 0 = 6553.5 А — положение максимума в спектре излучения СД при температуре 0 ºС, С = 2.62 Å /ºC — температурный коэффициент смещения, t — температура в ºС. Следует отметить, что значения λ 0 и С для каждого СД могут различаться. Как видно из рис. 1, б, при увеличении t на 10 ºС длина волны максимума излучения

а

б

Длина волны, нм

К к ц

20   22   24   26   28

Температура, ºС

Рис. 1. Зависимости спектра излучения СД от температуры.

а — смещение спектральной кривой для температур (ºС): 1 — 20.6, 2 — 20.8, 3 — 21.6, 4 — 24.1, 5 — 26.8, 6 — 29.6.

б — положение максимума спектральной кривой; точки — результаты эксперимента, их линейная аппроксимация рассчитана методом наименьших квадратов

увеличивается примерно на 3 нм. Следует отметить, что при таких измерениях требуется около тридцати минут на запись одного спектра, что в свою очередь требует высокой стабильности температуры СД.

Теперь рассмотрим определение максимума длины волны излучения с помощью эллипсометрии. Процесс измерения длины волны излучения СД на эллипсометре разделим на два этапа. Первый этап — это подготовка контрольного образца или предварительная калибровка эллипсометра. Второй — сам процесс измерения. Рассмотрим каждый этап по отдельности.

Первый этап

В качестве компенсатора для эллипсометра выбираем фазосдвигающую пластинку из кристаллического кварца (желательно, из искусственного кристаллического кварца [3]). Дисперсия и показатели преломления кристаллического кварца достаточно хорошо изучены [4–7]. Предварительно приближенное значение толщины фазосдвигающей пластинки — компенсатора достаточно измерить с точность 10 мкм, которую обеспечивают серийно выпускаемые микрометры. Затем эту фазосдвигающую пластинку устанавливаем на эллипсометр с источником излучения, имеющим известную длину волны (например, гелий—неоновый лазер с длиной волны излучения λ = = 632.8 нм). Из результатов эллипсометрических измерений определяем параметры компенсатора T и δ [8, 9]. Параметр Т характеризует отношение амплитудных (по модулю) коэффициентов пропускания фазосдвигающей пластинки (компенсатора) вдоль его "медленной" и "быстрой" осей, а δ — приобретаемый падающей световой волной на выходе пластинки сдвиг фазы между компонентами вектора электрического поля, параллельными этим осям. На практике чаще применяются схемы эллипсометра с фиксированным положением компенсатора. Причем компенсатор

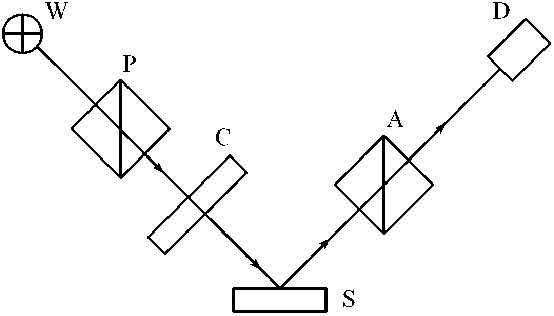
Рис. 2. Принципиальная схема эллипсометра. W — источник излучения, P — поляризатор, C — компенсатор, S — отражающая система, A — анализатор, D — приемник излучения может находиться как до отражающей системы, так и после нее. Рассмотрим схему эллипсометра, в которой компенсатор находится до отражающей системы, как показано на рис. 2. Для данной схемы азимутальные углы поляризационных элементов и параметры компенсатора T и δ связаны следующими соотношениями [9–11]:

tg( P_x - C )tg( P 2 - C )’

T

⁵ = arccose-  .     ( L а + L p cos² C ) x

2sin2 C                        (1)

x [tg( P - C ) - tg( P ₂ - C )]);

L _ sin( A 1 + A ₂ )    l _ sin( P 1 + P ₂ - 2 C )

А = sin( A, - A2) ’    P ”   sin(P1 - P2)   ’ где P1, P2 и А1, А2 — две пары неэквивалентных значений углов гашения поляризатора и анализатора при любом фиксированном значении угла поворота компенсатора С.

После определения параметров компенсатора из результатов эллипсометрических измерений на основе уравнений (1) аналогично методике, изложенной в работе [3], определяем точные значения толщины и показателей преломления этой фазосдвигающей пластинки.

Параметры компенсатора T и δ связаны с показателями преломления и толщиной пластинки соотношениями [9]:

T _ П 1    a 2 + b 1 ² ;

n 2 \ a 2 + b22 ’ a1,2 = (n1,2 + 1)2 - (n1,2

4 πd

^{- 1)2 cos}   ,    ⁿ 1,2 ;

λ b1,2    (n1,2

5 _ 5 o - 5 1 ;

5 _ arccos

—

4 πd

1)²sin λ n _1,2 ;

2 πd

⁵ 0 =    ,  ⁽ n 2 - n 1 ^);

λ a1 a 2 + b1 b2

4 ⁽ a^{2 +} О a 22 ⁺ b 2 ²⁾ ’

где n1,2 — показатели преломления фазосдвигающей пластинки для двух изонормальных волн, d — толщина фазосдвигающей пластинки, λ — длина волны светового излучения.

Второй этап

В эллипсометр устанавливаем источник излучения с неизвестной длиной волны. Опять определяем новые параметры компенсатора для этой неизвестной длины волны излучения из результатов эллипсометрических измерений. Теперь толщина фазосдвигающей пластинки точно известна. Аналогично методике, изложенной в работе [3], как и в предыдущем случае, определяем точные значения длины волны излучения и показателей преломления этой фазосдвигающей пластинки для данной длины волны. Если в первом случае неизвестной была толщина фазосдвигающей пластинки, то во втором — неизвестным параметром является длина волны источника излучения. Очевидно, что первый этап фактически сводится к калибровке прибора. Надо отметить, что такая методика на первый взгляд кажется сложной и относительно трудоемкой. Однако, если использовать в качестве компенсатора просветленную фазосдвигающую пластинку, то расчеты существенно упрощаются.

Для просветленной фазосдвигающей пластинки T = 1, δ 1 = 0 [12]. В этом случае δ = δ о и определяется из следующего выражения:

5 _

2 πd

^{( n} 2 ^{- n} 1 ). λ

Заметим, что при определенных значениях толщины (обозначим ее D o ) фазосдвигающей пластинки параметр δ принимает значения, кратные 2 π . Эту величину назовем полным периодом сдвига фазы (сдвиг фазы на 2 π ) фазосдвигающей пластины. Согласно (3), он определяется из следующего выражения:

D о _

λ

^{( n} 2 ^{- n} 1 ^).

(3а)

Очевидна зависимость D o от длины волны светового излучения, т. е. ее дисперсия. С учетом температурной зависимости фазосдвигающей пластинки из одноосного кристалла можно записать:

n 1 ^_ n o + — d t ;

dt dn n2 _ ne +--Ldt,

2 e dt где no и ne — показатели преломления для обыкновенной и необыкновенной волн, (dno/dt) и (dne/dt) — температурные коэффициенты показателей преломления для обыкновенной и необыкновенной волн. При фиксированном значении температуры окружающей среды n1 = no и n2 = ne.

Необходимо отметить, что для любой заданной длины волны существует дисперсионное значение полного периода сдвига фазы фазосдвигающей пластинки D o , которое определяется по формуле [7]:

D _o _ 119.27 Я + 5log( Z - 0.15) + 0.5 Л ⁴⁵ +

5.85

+-- - 7 7.59 мкм.

1 + 1.6Л²

Следует заметить, что выражение (4) приведено для кристаллического кварца при фиксированной температуре 22ºС и выполняется в интервале длин волн от 0.2 мкм до 3 мкм [6].

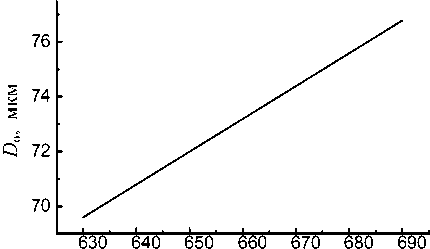
На рис. 3 представлены рассчитанные значения D o на основе выражения (4) для интересующего нас интервала длин волн. После математических преобразований можно показать, что для сдвига фаз δ можно получить достаточно простое соотношение с учетом дисперсии материала:

Длина волны, нм

Рис. 3. Дисперсионное значение полного периода фазосдвигающей пластины cd

632.6     632.8     633.0      633.2      633.4

Длина волны, нм

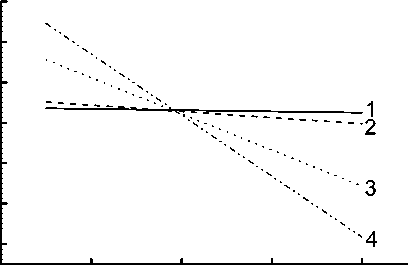
Рис. 4. Зависимость сдвига фаз от длины волны для нескольких значений толщины фазосдвигающей пластинки (в микрометрах): 1 — 17.5, 2 — 87, 3 — 507, 4 — 857

Здесь d — толщина фазосдвигающей пластинки; D o — значение полного периода для любой длины волны, определяемое соотношением (4); m — число полных периодов в толщине фазосдвигающей пластинки с учетом дисперсии. На рис. 4 показаны расчетные значения зависимости δ от длины волны λ для нескольких значений толщины фазосдвигающей пластинки, полученные на основе выражения (5). Как видно из рис. 4, по мере уменьшения толщины фазосдвигающей пластинки угол наклона зависимости сдвига фазы от длины волны стремится к нулю. Это особенно ярко иллюстрирует кривая 1 (рис. 4). С другой стороны, по мере увеличения толщины фазосдвигающей пластинки увеличивается чувствительность δ к изменению длины волны λ . Соответственно точность определения длины волны ограничивается конечностью толщины фазосдвигающей пластинки. Например, при толщине фазосдвигающей пластинки ~1 мм длину волны излучения можно определять с точностью ~0.001 нм.

ПРИМЕР ПРИМЕНЕНИЯ МЕТОДИКИ

В качестве примера рассмотрим определение длины волны и ее смещение от температуры для полупроводникового лазера с помощью эллипсометра. Выберем фазосдвигающую пластинку толщиной d = 860 мкм. Определяем точную толщину из результатов эллипсометрических измерений на длине волны 632.8 нм. Измеренное значение δ составляет 116.05º. Рассчитаем точную толщину пластинки. Для этого сначала переводим значение δ в доли полного периода, находим: δ = 0.32236. Из выражения (4) определяем значение D о для длины волны 632.8 нм: D о = 69.9322 мкм. Число полных периодов составит 12. Теперь нетрудно показать, что точная толщина d = 861.73 мкм.

В эллипсометр устанавливаем другой источник излучения, полупроводниковый лазер с λ ~660 нм. Для λ = 660 нм D o = 73.1905 мкм и m = 11. Из этих данных по формуле (5) определяем, что δ = = 278.56º. Экспериментально измеренное значение δ = 278.55º. Таким образом, расчетные и экспериментальные значения δ совпадают с точностью 0.01º, из чего следует, что длина волны нами выбранного экземпляра полупроводникового лазера при температуре 22 ºС равна 660 нм.

Теперь при фиксированном значении температуры (22 ºС) фазосдвигающей пластинки (компенсатора) проведем измерения длины волны излучения нашего полупроводникового лазера, нагретого до температуры 32 ºС. Измеренное значение δ компенсатора для полупроводникового лазера, нагретого до 32 ºC, составляет δ = 274.45º. Отсюда находим, что Dо = 73.2623 мкм. Следовательно, при температуре 32 ºС λ = 660.6 нм. Таким образом, при изменении температуры полупроводникового лазера на 10 ºС его длина волны изменяется на 0.6 нм. Откуда следует, что при точности определения эллипсометрических углов в 1 мин предложенная нами методика для толщины фазосдвигающей пластинки d = 861.73 мкм позволяет обнаружить изменение λ на 0.003 нм.

Такая методика может оказаться довольно эффективной для определения изменения длины волны под действием произвольного фактора. Надо отметить, что такой подход также позволяет быстро оценить длины волн излучения и их изменения для большого количества монохроматических или квазимонохроматических источников излучения, например СД.