Измерение магнитных моментов ферромагнитных наночастиц по положению линий ИК-спектра магнитной жидкости в магнитном поле

ВВЕДЕНИЕ                    тенсивности излучения с резонансной частотой,

В предыдущих наших работах наблюдался линейчатый ИК-спектр магнитной жидкости в магнитном поле [1]. На основании этого была высказана гипотеза о дискретности магнитных моментов однодоменных ферромагнитных наночастиц [2]. Было замечено, что по расположению пиков поглощения спектр похож на колебательновращательный спектр молекул [3], и исследована зависимость положений линий от индукции внешнего магнитного поля [4]. Получено, что положения максимумов колебательных линий, определяемые резонансными колебательными волновыми числами Kn,0 (n — колебательное квантовое число), от индукции внешнего магнитного поля не зависят, а положения максимумов вращательных линий, определяемые резонансными вращательными волновыми числами Kn,+J или Kn,–J (+J и –J — магнитные квантовые числа), при изменении индукции внешнего поля линейно меняются. В настоящей работе зависимость Kn,+J и Kn,–J от магнитной индукции объясняется тем, что вращательному моменту импульса наночастицы LJ, определяемому вращательным квантовым числом J, сопутствует магнитный момент РJ, имеющий зеемановскую энергию, равную его скалярному произведению на индукцию внешнего магнитного поля со знаком минус. Под действием ИК-излучения с резонансной частотой меняется ориентация магнитных моментов наночастиц в магнитном поле. Это вызывает изменение зеемановской энергии магнитных моментов наночастиц, приводящее к уменьшению или увеличению ин- что вызывает появление в спектре ИК-излучения пиков при резонансных волновых числах Kn,+J, Kn,–J. По значениям резонансных волновых чисел в ИК-спектре магнитной жидкости, полученном во внешнем магнитном поле с известной индукцией В, можно определять магнитные моменты наночастиц.

ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ МАГНИТНЫХ МОМЕНТОВ НАНОЧАСТИЦ ПО ЗНАЧЕНИЯМ РЕЗОНАНСНЫХ ВОЛНОВЫХ ЧИСЕЛ Kn,0, Kn,+J и Kn,–J В ИК-СПЕКТРАХ МАГНИТНОЙ ЖИДКОСТИ В МАГНИТНОМ ПОЛЕ

Предпосылки метода

На рис. 1–3 приведены ИК-спектры магнитной жидкости, полученные при трех индукциях внешнего магнитного поля. Значения индукций полей магнитов, в которых находилась магнитная жидкость при получении этих спектров:

В 1 = 255·10^–4, В 2 = 597·10^–4, В 3 = 663·10^–4Тл.

Эти значения, необходимые для расчета магнитных моментов наночастиц, были измерены с высокой точностью методом ядерного магнитного резонанса.* На этих рисунках вертикальными линиями обозначены положения максимумов пиков поглощения, соответствующих резонансным волновым числам Kn,0, Kn,+J, Kn,–J, по которым можно определять магнитные моменты наночастиц. Нижние индексы в обозначениях волновых чисел в поле рисунков для лучшего зрительного восприятия представлены в квадратных скобках, т. е., например, Kn,0 представлено как K[n,0].

Вариант 1. Определение РJ по резонансным волновым числам Kn,+J и Kn,–J

Фотон ИК-излучения с резонансным волновым числом Kn,+J вызывает переход наночастицы с колебательно-вращательного уровня, имеющего колебательное квантовое число n = 0, вращательное квантовое число J и магнитное квантовое число –J (при этом спин электронов наночастицы направлен против, а магнитный момент наночастицы направлен по индукции В), на колебательновращательный уровень, имеющий колебательное квантовое число n ˃ 0, вращательное квантовое число J и магнитное квантовое число +J (при этом спин электронов наночастицы направлен по, а магнитный момент наночастицы направлен против индукции В). В результате перехода усиливается колебательное движение магнитного момента наночастицы в поле сил межчастичных взаимодействий (на это затрачивается энергия фотона, равная hс(Kn,0 – K0,0)) и происходит поворот магнит- ного момента наночастицы на 180º в направлении против индукции магнитного поля (при этом магнитная энергия наночастицы в магнитном поле увеличивается, а энергия фотона уменьшается на 2РJB). Следовательно, энергия фотона с волновым числом Kn,+J равна Е1 = hcKn,+J = hс(Kn,0 – – K0,0 + 2РJВ). ИК-излучение с резонансным волновым числом Kn,–J вызывает переход наночастицы с колебательно-вращательного уровня, имеющего колебательное квантовое число n = 0, вращательное квантовое число, равное J, и магнитное квантовое число, равное +J (при этом спин электронов наночастицы направлен по, а магнитный момент наночастицы направлен против направления индукции В), на колебательно-вращательный уровень, имеющий колебательное квантовое число n ˃ 0, вращательное квантовое число J и магнитное квантовое число –J (при этом спин электронов наночастицы направлен против, а магнитный момент наночастицы по направлению индукции В). В результате перехода усиливаются колебания магнитного момента наночастицы и он поворачивается на 180˚ по направлению индукции В (его магнитная энергия уменьшается). Следовательно, энергия фотона с волновым числом Kn,–J равна Е2 = hcKn,–J = hс(Kn,0 – K0,0 – 2РJB). Разница энергий Е1 – Е2 = hс(Kn,+J – Kn,-J) = 4PJB, откуда

Р J = h·c· ( K n,+J – K n,–J ) / (4 В ). (1)

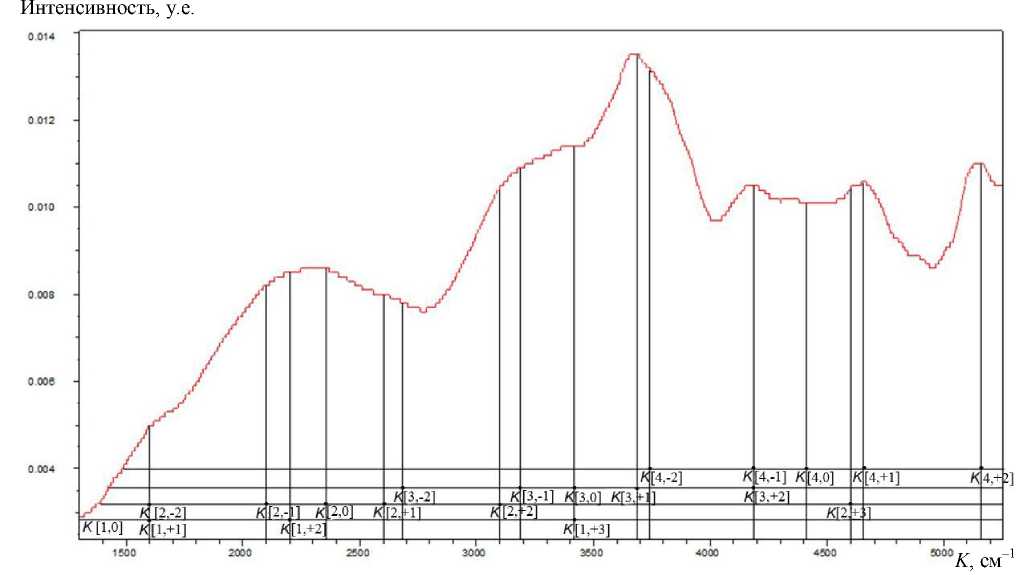
Рис. 1. ИК-спектр магнитной жидкости в магнитном поле с индукцией В 1 = 255·10^–4Тл

Рассмотрим спектр, представленный на рис. 1 ( В = В 1 = 255·10^–4 Тл). В этом спектре видны симметрично расположенные вращательные линии колебательно-вращательных серий с n = 3 и n = 4. Рассмотрим колебательно-вращательную серию с n = 3. На нижнем вращательном уровне с резонансным волновым числом ¹ K 3,–1 = 3180 см^–1 (верхний индекс указывает номер рисунка) магнитный момент P 1 ориентирован под острым углом к индукции магнитного поля В , а на верхнем вращательном уровне с резонансным волновым числом ¹ K 3,+1 = 3680 см^–1 магнитный момент P 1 ориентирован под тупым углом к индукции магнитного поля В . Поэтому фотоны с бόльшим волновым числом (¹ K 3,+1 ) отклоняют направления магнитных моментов от направления индукции поля, при этом их энергия поглощается, а фотоны с меньшим волновым числом (¹ K 3,–1 ) приближают ориентацию магнитных моментов к направлению индукции поля, при этом их энергия возрастает. Можно сделать вывод, что после прохождения через магнитную жидкость различие энергий фотонов с волновыми числами ¹ K 3,+1 и ¹ K 3,–1 равно удвоенному различию энергий магнитного момента Р 1 , ориентированного по полю и против поля. Таким образом, по формуле (1) можно рассчитать магнитный момент наночастиц Р 1 при n = = 3:

Р 1,3 = hс· (¹ K 3,+1 – ¹ K 3,–1 ) / (4 В 1 ) = (6.6·10^–34 · 3·10⁸ × × (3680 – 3180) · 10² / (4 · 0.0255) = 6.6 · 3 · 500 × × 10^–34+8+2/(4·0.0255) = 0.97·10^–19 Ам².

Аналогично при n = 3 можно рассчитать Р 2 по волновым числам ¹ K 3,+2 = 4180 см^–1 и ¹ K 3,–2 = = 2670 см^–1:

Р 2,3 = hс· (¹ K 3,+2 – ¹ K 3,–2 )·10² / (4 В 1 ) = 6.6·10^–34 × × 3·10⁸ · (4180 – 2670)·10² / (4·0.0255) = 6.6·10^–34 × × 10⁸·1510·10²/ (4·0.0255) = 2.93·10^–19 Ам².

На рис. 2 ( В = В 2 = 597·10^–4 Тл) видны вращательные линии с ² K 3,+1 = 4030 см^–1 и ² K 3,–1 = = 2830 см^–1. По этим линиям можно при n = 3 определить

Р 1,3 = hс ·(² K 3,+1 – ² K 3,–1 ) / (4 В 2 ) = 6.6·10^–34 × × 3·10⁸ ·(4030 – 2830) · 10² / (4·0.0597) = 19.8 × ×1200 ·10^–34+8+2 / (4·0.0597) = 0.995·10^–19 Ам².

Видны также линии с ² K 2,+1 = 3020 см^–1 и ² K 2,–1 = = 1730 см^–1. По этим линиям можно при n = 2 определить

Р 1,2 = hс ·(² K 2,+1 – ² K 2,–1 ) / (4 В 2 ) = 6.6× ×10^–34 ·3 · 10⁸ · (3020 – 1730) · 10² / (4·0.0597) = = 6.6·3·1290·10^–34+8+2/ (4·0.0597) = 1.07·10^–19 Ам².

Интенсивность, у.е.

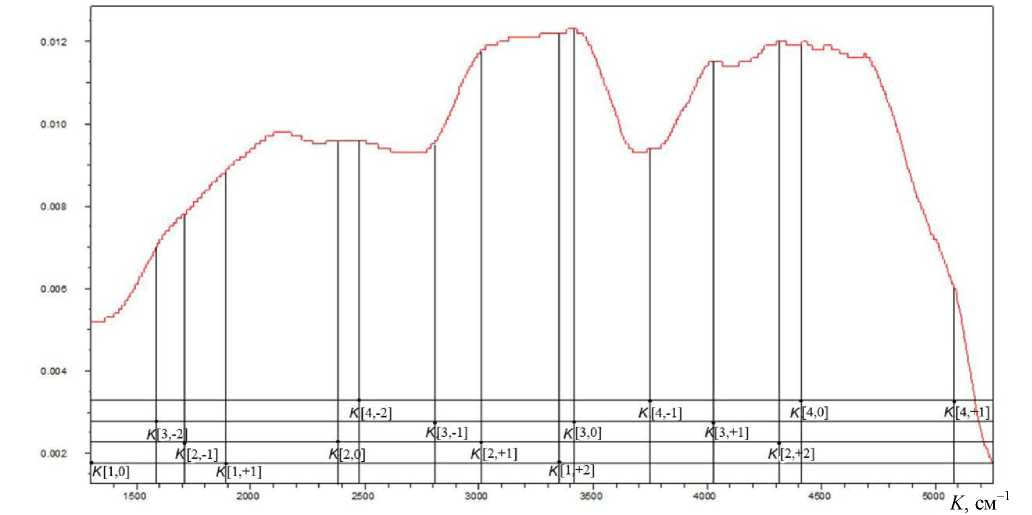
Рис. 2. ИК-спектр магнитной жидкости в магнитном поле с индукцией В 2 = 597·10^–4 Тл

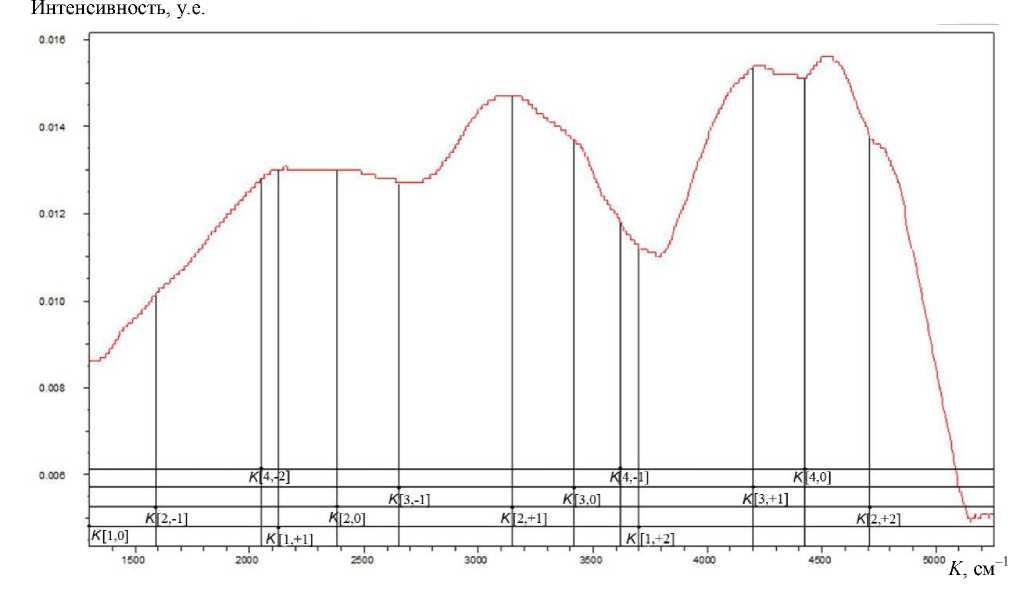
Рис. 3. ИК-спектр магнитной жидкости в магнитном поле с индукцией В 3 = 663·10^–4 Тл

На рис. 3 ( В = В 3 = 663·10^–4 Тл) видны вращательные линии с ³ K 2,+1 = 3150 см^–1 и ³ K 2,–1 = = 1580 см^–1. По этим линиям можно при n = 2 определить

Р 1,2 = hс ·(³ K 2,+1 – ³ K 2,–1 ) / (4 В 3 ) = 6.6·10^–34 · 3 × × 10⁸ · (3150 – 1580) · 10² / (4·0.0663) = 6.6 · 3 × × 1570 · 10^–34+8+2/ (4·0.0663) = 1.17·10^–19Ам².

Видны также линии с волновыми числами ³ K 3,+1 = 4200 см^–1 и ³ K 3,–1 = 2640 см^–1. По этим линиям можно при n = 3 определить

Р 1,3 = hс ·(³ K 3,+1 – ³ K 3,-1 ) / (4 · В 3 ) = 6.6·10^–34·3× ×10⁸ · (4200 – 2640)·10² / (4·0.0663) = 6.6·3× ×1560·10^–34+8+2/ (4· 0.0663) =1.16·10^–19Ам².

Вариант 2. Определение РJ по резонансным волновым числам Kn,0, Kn,+J или Kn,0, Kn,–J

Фотон ИК-излучения с резонансным волновым числом Kn,+J вызывает переход наночастицы с колебательно-вращательного уровня, имеющего колебательное квантовое число n = 0, вращательное квантовое число J и магнитное квантовое число равное –J (магнитный момент направлен по В), на колебательно-вращательный уровень, имеющий колебательное квантовое число n ˃ 0, вращательное квантовое число J и магнитное квантовое число, равное +J (магнитный момент направлен против В). В результате магнитный момент наночастицы РJ начинает интенсивнее колебаться в поле сил межчастичного взаимодействия (на это затрачивается энергия излучения hс·(Kn,0 – K0,0) и поворачивается в направлении против индукции В (на это затрачивается энергия излучения 2РJВ). Следовательно, энергия фотона с волновым числом Kn,+J равна Е1 = hc·Kn,+J = = hс·(Kn,0 – K0,0 + 2РJВ). Фотон ИК-излучения с волновым числом Kn,0 вызывает переход наночастицы с колебательного уровня, имеющего колебательное квантовое число n = 0, вращательное квантовое число J и магнитное квантовое число, равное 0, на колебательный уровень, имеющий колебательное квантовое число n ˃ 0, вращательное квантовое число J и магнитное квантовое число, равное 0. При этом возникают колебания, на которые расходуется энергия фотона Е2 = hс·(Kn,0 – K0,0). Разница энергий фотонов Е2 – – Е1 = 2РJВ. Следовательно, магнитный момент наночастицы можно найти из выражения

Р J = hc ·( K n,+J – K n,0 ) / (2 B ). (2)

Фотон ИК-излучения с резонансным волновым числом Kn,–J вызывает переход наночастицы с колебательно-вращательного уровня, имеющего колебательное квантовое число n = 0, вращательное квантовое число равное J и магнитное квантовое число равное +J (при этом спин наночастицы направлен по В, а магнитный момент наночастицы направлен против В), на колебательновращательный уровень, имеющий колебательное квантовое число n ˃ 0, вращательное квантовое число J и магнитное квантовое число, равное –J (при этом спин наночастицы направлен против В, а магнитный момент наночастицы направлен по В). В результате воздействия ИК-излучения магнитный момент наночастицы РJ начинает интенсивнее колебаться в поле сил межчастичного взаимодействия, поворачивается по направлению индукции В, и его энергия в магнитном поле уменьшается на 2РJВ. При этом поглощается энергия фотона hc·Kn,–J = hс·(Kn,0 – K0,0 – 2РJВ). Магнитный момент наночастицы можно найти из выражения

Р J = hc ·( K n,0 – K n,–J ) / (2 В ). (3)

На рис. 1 ( В = В 1 = 255·10^–4 Тл) видны линии с волновыми числами ¹ K 2,0 = 2370, ¹ K 2,–2 = 1600, ¹ K 2,+3 = 4600, ¹ K 3,0 = 3430, ¹ K 3,+1 = 3680, ¹ K 3,+2 = 4180, ¹ K 4,0 = 4420, ¹ K 4,+1 = 4680 см^–1. По этим волновым числам по формулам (2, 3) можно при n = 2 найти

Р2,2 = hс·(1K2,0 – 1K2,–2) / (2В1) = 6.6·10–34 ·3 ·108 × ×(2370 – 600) · 102 / (2 · 0.0255) = 6.6·3·770 / (2 × ×0.0255)·10–34+8+2= 2.99·10–19 Ам2, при n = 3 найти

Р1,3 = hс·(1K3,+1 – 1K3,0) / (4В1) = 6.6·10–34·3·108 × ×(3680 – 3430)·102 / (2·0.0255) = 3·6.6·250 / (2× ×0.0255) ·10–34+8+2= 0.97·10–19Ам2, при n = 3 найти

Р2,3 = hс·(1K3,+2 – 1K3,0) / (2В1) = 6.6·10–34·3·108 × ×(4180 – 3430)·102 / (2 · 0.0255) = 6.6·3·750 / (2 × ×·0.0255) ·10–34+8+2 = 2.91·10–19Ам2, при n = 4 найти

Р1,4 = hс·(1K4,+1 – 1K4,0) / (2В1) = 6.6·10–34·3· 108 × ×(4680 – 4420) ·102 / (2·0.0255) = 6.6 · 3 · 260 / (2× ×0.0255)·10–34+8+2= 1.01·10–19 Ам2, при n = 2 найти

Р 3,2 = hс ·(¹ K 2,+3 – ¹ K 2,0 ) / (2 В 1 ) = 6.6·10^–34· 3× ×10⁸ ·(4600 – 2370)·10² / (2·0.0255) = 6.6·3 ·2230 × ×10^–34+8+2/ (2·0.0255) = 8.66·10^–19 Ам².

На рис. 2 ( В = В 2 = 597·10^–4 Тл) различаются линии с волновыми числами ² K 3,0 = 3430, ² K 3,+1 = = 4030 см^–1. По этим волновым числам можно при n = 3 найти магнитный момент

Р 1,3 = hс ·(² K 3,+1 – ² K 3,0 ) / (2 В 2 ) = 6.6·10^–34·3 × × 10⁸ · (4030 – 3430)·10² / (2·0.0597) =

= 6.6·3·600·10–34+8+2/ (2·0.0597) = 0.995·10–19 Ам2.

На рис. 3 (В3 = 663·10–4 Тл) видны линии с резонансными волновыми числами 3K4,0 = 4420, 3K4,–1 = 3630, 3K4,–2 = 2050 см–1. По этим значениям резонансных волновых чисел можно при n = 4 оп- ределить магнитные моменты:

Р 1,4 = hс ·(³ K 4,0 -– ³ K 4,–1 ) / (2В 3 ) = 6.6·10^–34·3·10⁸ × ×(4420 – 3630)·10² / (2·0.0663) = 6.6·3·790 / (2× ×0.0663)·10^–34+8+2= 1.18·10^–19 Ам²

и Р 2,4 = hс ·(³ K 4,0 – ³ K 4,–2 ) / (2В 3 ) = 6.6·10^–34·3·10⁸ × ×(4420 – 2050)·10² / (2·0.0663) = 6.6·3·2370× ×10^–34+3+2/ (2·0.0663) = 3.54·10^–19 Ам².

По линиям с волновыми числами ³ K 2,0 = = 2370 и ³ K 2,+2 = 4700 см^–1 можно при n = 2 определить магнитный момент

Р 2,2 = hс ·(³ K 2,+2 – ³ K 2,0 ) / (2В 3 ) = 6.6·10^–34·3·10⁸ × ×(4700 – 2370)·10² / (2·0.0663) = 6.6·3·2330× ×10^–34+8+2/ (2·0.0663) = 3.48·10^–19 Ам².

По линиям с волновыми числами ³ K 2,0 = = 2370, ³ K 2,+1 = 3150, ³ K 2,+2 = 4700 см^–1 можно при n = 2 определить

Р 12 = hс ·(³ K 2+1 – ³ K 20 ) / (2В 3 ) = 6.6·10^–34· 3 × , ,,

×108·(3150 – 2370)·102 / (2·0.0663) = 6.6·3·780× ×10–34+8+2/ (2·0.0663) = 1.164·10–19 Ам2

и Р 2,2 = hс ·(³ K 2,+2 – ³ K 2,0 ) / (2В 3 ) = 6.6·10^–34 ·3× ×10⁸ ·(4700 – 2370)·10² / (2·0.0663) = 6.6·3 × ×2330·10^–34+8+2/ (2·0.0663) = 3.48·10^–19 Ам².

АНАЛИЗ ИЗМЕРЕННЫХ ПО ПОЛОЖЕНИЯМ ЛИНИЙ ИК-СПЕКТРА ЗНАЧЕНИЙ МАГНИТНЫХ МОМЕНТОВ НАНОЧАСТИЦ

Зависимость значений магнитных моментов наночастиц от индукции магнитного поля

Обозначим магнитные моменты наночастиц Р J , измеренные по резонансным волновым числам K n,+J или K n,–J (при колебательном квантовом числе n и вращательном квантовом числе J), индексами Р J,n и напишем их в единицах 10^–19 Ам² в порядке возрастания В , J и n.

В = В 1 = 0.0255 Тл,

J = 1: Р 1,3 = 0.97, Р 1,4 = 1.1, Р 1,3 = 0.97;

J = 2: Р 2,3 = 2.93, Р 2,2 = 2,99, Р 2,3 = 2,91;

J= 3: Р 3,2 = 8.66.

Средние значения: Р 1 = 0.98, Р 2 = 2.94, Р 3 = 8.66.

В = В 2 = 0.0597 Тл,

J = 1: Р 1,2 = 1.07, Р 1,3 = 0.995, Р 1,3 = 0.995.

Среднее значение Р 1 = 1.02.

В = В 3 = 0.0663 Тл,

J = 1: Р 1,2 = 1.17, Р 1,3 = 1.16, Р 1,4 = 1.18, Р 1,2 = = 1.16;

J = 2: Р 2,4 = 3.54, Р 2,2 = 3.48.

Средние значения: Р 1 = 1.17, Р 2 = 3.51.

Из этих результатов видно, что измеренные значения магнитных моментов наночастиц Р J от колебательного квантового числа n практически не зависят, а с ростом индукции В в 1.11, 2.3 и 2.6 раза увеличиваются соответственно в 1.07, 1.12 и 1.2 раза. Независимость магнитных моментов наночастиц от колебательного квантового числа можно объяснить тем, что магнитные свойства связаны с вращательным движением зарядов, а не с их колебаниями. Зависимость значений магнитных моментов наночастиц от индукции магнитного поля можно объяснить тем, что причиной дискретности магнитных моментов является квантование моментов импульса наночастиц, а рост магнитных моментов наночастиц связан с увеличением гиромагнитных отношений доменов с ростом В .

Связь магнитных моментов и моментов импульса наночастиц

Как уже говорилось, обнаруженную зависимость магнитных моментов наночастиц от индукции внешнего магнитного поля можно объяснить тем, что их дискретность вызвана квантованием моментов импульса наночастиц. На опыте двум измеренным при В = В 1 дискретным значениям магнитного момента Р 1 = 0.98 и Р 2 = 2.94 и измеренным при В = В 2 дискретным значениям Р 1 = = 1.17 и Р 2 = 3.5 соответствуют дискретные значения моментов импульса L J = h ·(J·(J + 1))^0.5, равные L 1 = h ·(2)^0.5 = 1.41· h и L 2 = h ·(6)^0.5 = 2.45· h . Из этих значений следует, что ( Р 2 / Р 1 ) = ( L 2 / L 1 )², т. е. магнитный момент наночастицы пропорционален квадрату еe момента импульса. Это может быть следствием пропорциональности обменного интеграла, определяющего энергию обменного взаимодействия, вызывающего появление магнитного момента однодоменной наночастицы, произведению спинов взаимодействующих атомов. Иначе это можно объяснить тем, что намагниченность магнитной жидкости, которая равна сумме магнитных моментов наночастиц в 1м³, определяется законом Бриллюэна, согласно которому она пропорциональна h ²J·(J + 1), т. е. квадрату момента импульса наночастиц.

СРАВНЕНИЕ МАГНИТНЫХ МОМЕНТОВ НАНОЧАСТИЦ, ИЗМЕРЕННЫХ ПО ПОЛОЖЕНИЮ ВРАЩАТЕЛЬНЫХ ЛИНИЙ ИК-СПЕКТРА И ПО КРИВОЙ НАМАГНИЧИВАНИЯ МАГНИТНОЙ ЖИДКОСТИ

Как следует из ИК-спектра магнитной жидкости, полученного при n < 3, в ней имеются наночастицы с тремя средними дискретными значе- ниями магнитных моментов Р1 ≈ 1.0·10–19, Р2 = 3.2·10–19, Р3 = 8.7·10–19 Ам2. Обычно магнитные моменты наночастиц в магнитных жидкостях измеряют сравнением экспериментальной кривой намагничивания с формулой Ланжевена. Этим методом для разных магнитных жидкостей были получены следующие значения магнитных моментов наночастиц в единицах 10–19 Ам2:

• 4.4 [5], 4.3; 6.2; 12.3 [6], 7.0 [7], 4.7; 4.3; 3.49; 5.68 [8], 4.6 [9], 2.4; 2.7; 8.6; 12.8; 14.2; 12.3 [10], 1.6; 1.3; 1.0; 0.8 [11].

0.8×10–19, 1.0·10–19, 2.4·10–19, 2.7·10–19Ам2, преобладают наночастицы с J = 1;

• 4.3·10^–19, 4.4·10^–19, 4.7·10^–19, 3.49·10^–19, 5.68× ×10^–19 Ам²,

• 6.2·10^–19, 7.0·10^–19, 8.6·10^–19, 5.68·10^–19Ам²,

• 12.8·10^–19, 12.3×10^–19, 14.2·10^–19Ам²,

При сравнении значений магнитных моментов, полученных по ИК-спектру и по кривой Ланжеве-на, наиболее важно, что несмотря на принципиальное различие методик измерения по порядку величины эти значения совпадают. При сравнении конкретных значений следует учесть, что по кривой намагничивания определяются средние значения магнитных моментов наночастиц в магнитной жидкости Р ср , которые зависят от соотношения наночастиц с разными J. Например, можно предположить, что в жидкостях со средними значениями Р ср , равными

в жидкостях со средними значениями Р ср , равными

преобладают наночастицы с J = 2;

в жидкостях со средними значениями Р ср , равными

преобладают частицы с J = 3;

в жидкостях со средними значениями Р ср , равными

преобладают наночастицы с J ˃ 3.

ЗАКЛЮЧЕНИЕ

Основные результаты настоящей работы состоят в следующем.

• 1.    Магнитные моменты однодоменных ферромагнитных наночастиц в магнитных жидкостях имеют дискретные значения.

• 2.    Магнитные моменты наночастиц пропорциональны квадратам их моментов импульса.

• 3.    Средний магнитный момент наночастиц в магнитной жидкости зависит от соотношения наночастиц с разными значениями момента импульса.

• 4.    Несмотря на принципиальное различие методов измерения магнитных моментов по кривой намагничивания и по ИК-спектру магнитной жидкости, этими методами получаются близкие значения магнитных моментов наночастиц.

• 5.    Магнитный момент наночастицы при постоянном значении момента импульса увеличивается с увеличением индукции внешнего магнитного поля.