Измерение параметров сигналов в многопозиционной радиолокационной системе при воздействии коррелированных помех

Для повышения точности измерения энергетических параметров при воздействии коррелированных помех

предусматривается оценка интенсивности полезного сигнала в пунктах приема. При разнесении приемных пунктов на базу, большую, чем ожидаемый радиус пространственной корреляции сигнала, когерентная многопозиционная обработка заменяется некогерентной. В случае обеспечения высокой помехозащищенности приемных пунктов, т. е. при достаточном отношении сигнал / шум осуществляется переход от некогерентной междупунк-товой обработки сигналов к соответствующей междупун-ктовой обработке координатной информации, полученной в каждом приемном пункте.

Малобазовая многопозиционная радиолокационная система (МП РЛС) состоит из передающего пункта и L произвольно расположенных приемных пунктов с фазированной антенной решеткой (ФАР). Полагаем, что цели и постановщики активных помех находятся в дальней зоне, а доплеровские смещения частот колебаний от них в пунктах приема незначительны [1]. Модели внутренних

ln l =

Z ² 4 1 + 5 2 2

- In 1 + q- .

Здесь весовая интегральная сумма Z и параметр обнаружения сигналов д ² определяются выражениями [1]:

N -1

Z = (2 N )-1 £ YT (f) к * (f, %),(3)

f =0

N -1

q2 =(2N )-1 £ XT (f, %) к * (f, %),(4)

tf где N =--число дискрет выборки входной реализа-Д t ции на интервале наблюдения Т, при шаге дискретизации

Д t , выбранном в соответствии с теорией Котельникова; K ( f , %) - весовой вектор оптимальной пространственно-частотной обработки; * - знак комплексного сопряжения; Т - знак транспонирования; д ² - отношение сиг

нал / (шум + помеха) на выходе устройства оптимальной

шумов и внешних помех охарактеризуем гауссовскими центрированными стационарными случайными процес

обработки.

Весовой вектор K ( f , % )

может быть записан в виде

сами для комплексных амплитуд, а модели отраженных от цели сигналов соответственно гауссовой статистикой для комплексного амплитудного множителя. В этом случае модель принимаемых МП РЛС пространственно-временных колебаний (1), представленную дискретно в частотной области, можно записать в виде аддитивной смеси

K ( f , % ) = 2Ф ^{- 1} ( f ) X ( f , % ) ,          (5)

здесь Ф( / ) - матрица спектральных плотностей мощности

L

Y( f ) = лрX( f, %) + £X ( f, V) + X„ ( f ) , l=1

где A - дискретное значение наличия цели (А =

1,0);

в = diag ( в i ) - блочная диагональная матрица комплексных амплитудных множителей; X ( f , % ) - блочный вектор-столбец амплитудно-фазовых распределений (АФР) в МП РЛС с учетом дискретного частотного описания структуры сигнала; % - вектор информативных параметров сигнала; X l ( f , % l ) - блочный вектор АФР помех от I- го источника для дискретной частоты / , X „ ( f ) - блочный вектор АФР шумов для дискретной частоты /

Блоки составных векторов относятся к соответствующему АФР сигнала и помех на ФАР в пунктах приема.

На основе принятого вектора-столбца входных воздействий У ( / ) требуется вывести решение о наличии или

помех и шумов, учитывающая корреляционные связи помеховых колебаний по элементам антенной системы [1].

В алгоритме предусмотрено когерентное суммирование сигнала с весами, обеспечивающими накопление сигнала и подавление коррелированных помех. Оценка информативных параметров находится как аргумент максимума логарифма отношения правдоподобия. Потенциальная точность измерения параметров вектора первичных измерений характеризуется матрицей точности

d 2 ln | Y

\ % д%.-д%.

ij

Ее диагональные элементы

Г = —⁵--

% ’ ( Д% , ) ²

пропорциональны параметру обнаружения и обратно

отсутствии полезных отраженных сигналов и измерить их параметры. Достаточной статистикой при обнаружении флуктуирующего сигнала (1) является логарифм отношения правдоподобия [1]

пропорциональны квадрату разрешения по параметру Д% i . Высокая точность определения координат цели в многопозиционной когерентной системе обеспечивается за счет достаточно высокой эффективности помехоза-щиты (большим отношением сигнал / шум) и высокой разрешающей способностью по угловым координатам

за счет разнесения в пространстве приемных пунктов. Однако наличие разрывной апертуры приводит к необходимости организации многоканальных широкополосных линий связи и принятия специальных мер по устранению неоднозначности измерения угловых координат целей. Несмотря на высокую эффективность оптимальной обработки сигналов в МП РЛС, ее практическая реализация может оказаться трудно выполнимой задачей в реальном масштабе времени. В связи с этим рассмотрим квазиоптимальные алгоритмы измерения информативных параметров с разделяющейся внутрипунктовой и междупунктовой обработкой.

Математическим условием разделения внутрипунктовой и междупунктовой обработки сигналов является факторизация блочных спектральных плотностей мощностей помех. Так, например, для идентичных ФАР в приемных пунктах прямая и, соответственно, обратная матрицы спектральных плотностей мощности может быть представлена в виде кронекеровского произведения [1]

Ф " ¹ ( f ) = Ф вп ( f ) ® Ф^ ( f ) , (8) где ® - знак кронекеровского произведения; Ф_вп ( f ) и Ф_мп ( f ) - матрицы спектральной плотности мощности помех между элементами ФАР и пунктами приема соответственно.

При аналогичном представлении модели сигнала вектор весовых коэффициентов имеет вид

K ( f ,X ) = K вп ( f .X ) ® K мп ( f .^ ) , (9)

Причем, в пренебрежении запаздыванием огибающих входных колебаний на апертуре ФАР, внутрипунктовая пространственно-временная обработка определяется весовым вектором пространственной обработки (10)

Rвп (х ) = Фвп (f) Xвп (х„р), (10) и временной структурой ожидаемого сигнала А-(t, %пр), так что квп (X, t ) = Rвп (^„р) X (t Ар), (11) где Хпр, Хвр - пространственные и временные информативные параметры соответственно.

Для вычисления логарифма отношения правдоподобия (2) с учетом (9) для междупунктовой обработки достаточно одноканальных широкополосных линий связи. Благодаря внутрипунктовой и междупунктовой обработке с учетом корреляционных свойств помеховых колебаний осуществляется достаточная эффективность поме-хозащиты МП РЛС и сохраняется возможность защиты от постановщиков помех, действующих по главным лепесткам характеристик направленности отдельных пунктов.

Для эффективной помехозащиты необходимо применять специальные меры в каждом пункте в целях исключения подавления помех в главном лепестке диаграммы направленности (ДН). Также необходимо обеспечить передачу вышеназванных помех в пункт обработки информации (ПОИ), что предполагает наличие широкополосных линий связи.

В силу сложности реализации вышеназванных условий и ограниченного радиуса пространственной корреляции сигналов и помех в целях упрощения алгоритма обработки можно отказаться от когерентного междупун- ктового накопления сигнала и компенсации помех, а при достаточном отношении сигнал / шум в каждом из пунк тов приема и от некогерентного накопления сигналов между пунктами. Последнее практически эквивалентно заменяется междупунктовой обработкой результатов измерения координат целей. Оценки информативных параметров Xi, полученные в каждом из пунктов, объединяются в результирующую оценку а с учетом пересчета в единую систему координат [2]

L а = ср* |Х с«i аx ,(12)

V l _L J

Cр    1 Cаl,(13)

l аi — h (Xi ),(14)

Cal — hl ( CX, ) ,( где exl - оценка координат вектора состояния цели в /-ом пункте приема; Cа - корреляционная результирующая матрица точности измерения декартовых координат; h (Xl) - векторная нелинейная функция пересчета координат цели; h (Cxl) - векторная нелинейная функция пересчета матрицы точности из сферической в декарто ву систему координат.

Для определения входящих в результирующее значение оценок матриц точности необходимо знать отношение сигнал / (помеха + шум) в пунктах приема. Кроме того, актуальность задачи оценивания отношения сигнал / (помеха + шум) обусловлена энергетическим характером информационных параметров в условиях воздействия коррелированных помех. Для моделей отраженного сигнала со случайной фазой и случайной амплитудой отмеченная задача сводится к оцениванию комплексных амплитуд или интенсивностей принимаемых сигналов на фоне помех. Требуемая статистика в /-ом пункте в этом случае определяется выражениями для сигнала со случайной начальной фазой [1]

ln l — 2

| Z ( X )| ² q ² ( X )

при однократной оценке амплитуды z (X) bl(X) — 2 q2lX), для сигнала со случайными начальной фазой и амплитудой ll(X) —

|Z l ( X )|² b’ l     , f b.q 2 ( X )

ln f bpq2 (X) + 1)4

.

b. — M { b l ² } ,

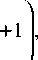
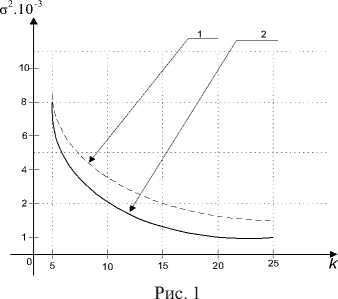
при однократной оценке интенсивности сигнала

Z*(X)

b-—4 qw" 5Й.

Таким образом, основные операции выбранного алгоритма получения координатной информации о целях в условиях помех, определяющих структуру МП РЛС, сво дятся к когерентному накоплению сигнала и компенса- ции помех, получению оценок интенсивностей сигнала и информативных параметров в пунктах приема и между-пунктовой обработки координатной информации с учетом точности первичных измерений.

В условиях адаптации к воздействию активных помех происходит изменение ДН фазированных решеток в пунктах приема, что приводит к возникновению систематических и росту флуктуационных ошибок [3]. В частности, при действии помех в первых боковых либо в области главных лепестков характеристики ДН, возникает систематическая ошибка, которая в ряде случаев превышает половину ширины ДН. Указанное смещение устраняется путем дополнительных измерений интенсивностей полезных колебаний. В последнем случае, однако, возрастают флуктуационные ошибки однократных измерений. С целью их снижения предложено производить усреднение оценок интенсивности сигнала [3; 4]. В работе рассматривается возможность повышения точности измерения параметров радиолокационного сиг

цы точности текущего измерения параметров определяются как

_ д² ln l

^{Cy + 1} ""Ю ²"

^

с = у 22

д ² ln l

д(Ь2 Г

С = С =

^C 12    C y +2

^^^^^^в

^d 2^ln l. . де-д ( ь :)

Результаты моделирования работы следящих измерителей - одного, построенного на основе статистики, инвариантной к энергии сигнала, и второго, реализующего совместное следящее измерение угловой координаты и средней энергии сигнала, приведены на рис. 1.

нала путем использования адаптивного алгоритма следящего измерения, реализующего совместную фильт

рацию оценок угловых координат цели и оценок энергии сигнала.

Для адаптивных алгоритмов, использующих оценку

энергии сигнала, существенным является вопрос, связанный с получением такой оценки. Действительно, оценить

энергию сигнала можно по нескольким входным реализациям. При этом вектор информативных параметров от реализации к реализации будет изменяться, что обусловлено движением цели. Отсюда следует необходимость

использования совместного следящего измерения координат цели и интенсивности сигнала.

Для синтеза совместного следящего измерителя будем полагать, что вектор информативных параметров л

содержит угловую координату и и энергию полезного сигнала. В соответствии с уравнением фильтрации оце

нок при следящем измерении результирующая оценка на к+ 1 шаге будет равна [1]

-1

^X k +1 " ^X ok +1 ^{+ C}pk +1 ^Cyk +1 ( ^X yk +1

^^^^^^в

^X ok +1 ) ^,

А где Xok+1 - прогнозированное значение оценок и и b2,

полученных путем пересчета результирующей оценки к- го шага фильтрации; X _{yk + 1} - текущая оценка вектора л; C_yk +i - матрица точности текущих измерений; C^ _{+ 1} -результирующая матрица ошибок следящего измерения

Здесь показаны зависимости дисперсий ошибок следящего измерителя, инвариантного к энергии сигнала (кривая 1), и измерителя, реализующего алгоритм (19)-(20) (кривая 2) от числа шагов фильтрации.

Из анализа графиков следует, что точность измерения угловых координат во втором измерителе в 1,5-2 раза выше, чем в измерителе, инвариантном к энергии сигнала.

На основе аналитических соотношений для оценок первичных и результирующих измерений (12)-(15) получим количественные оценки для средних квадратических ошибок (СКО) в МП РЛС в зависимости от числа приемных пунктов и сравним их со значениями СКО, рассчитанными для двухпозиционной оптимальной когерентной обработки сигнальной информации.

На рис. 2 представлены зависимости нормированных к базе (здесь база - расстояние между передающим и приемными пунктами) СКО оценивания координаты х от

на к+ 1 шаге.

свою очередь, величина

^Cyk +1 ( ^X yk +1

^^^^^^в

^X ok +1

представляет собой взвешанные невязкие и может быть полученные путем дифференцирования статистики (17)

по соответствующим параметрам, т. е.

. д ln l . д ln l

^    - • ^А 2       -

Результирующая матрица точности С к _{+ 1} на к+ 1 шаге определяется равенством

С. = С , + С , k +1     ^Vo1: +1 ⁺ У^ук +1 ,

где С _{ок+ 1} - прогнозированное значение матрицы точности на к+ 1 шаге, получаемое путем пересчета результирующей матрица точности к- го шага. Элементы матри

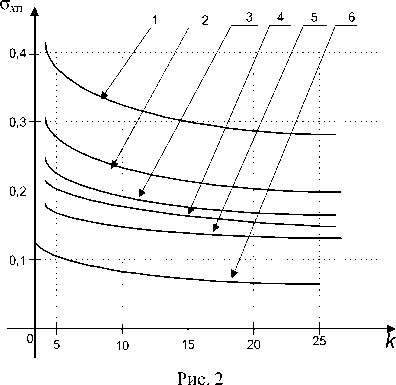
числа шагов поступления информации к . Как показали результаты расчетов, характер изменения соответствующих величин по осям Уи2 аналогичен приведенным на рис. 2. Здесь кривая под номером 6 соответствует характеру изменения о =f(К) для оптимальной двухпозиционной когерентной обработки, кривые 1-5 - для МП РЛС, причем номер кривой соответствует количеству пунктов приема участвующих в обработке принятых колебаний. Из анализа кривых (рис. 2) следует, что даже при некогерентной обработке принятых колебаний в МП РЛС, состоящей из пяти приемных пунктов, СКО измерения координаты х в 1,2-1,8 раза превышает соответствующие значения СКО для двухпозиционной оптимальной когерентной обработки сигнальной информации.

Таким образом, можно сформулировать следующие выводы:

• 1.    Проведен качественный анализ алгоритмов измерения информативных параметров сигнала в малобазовой МП РЛС, полученных на основе оптимального решения задачи оценивания методами математической статистики. Несмотря на высокую потенциальную точность оценок в когерентной МП РЛС, ограничения, связанные с радиусом пространственной корреляции сигнала и помех, неоднозначностью угловых измерений на разрывных апертурах, сложностью реализаций широкополосных многоканальных линий связи, приводят к постановке задачи определения алгоритмов измерения и анализа их точности в некогерентной МП РЛС.

• 2.    Качественный анализ квазиоптимальные алгоритмов обработки в когерентной МП РЛС свидетельствует о возможности перехода от некогерентной междупункто-вой обработки сигнала к междупунктовой обработке координатной информации. Ухудшением точности измерения при указанном переходе можно пренебречь в случае регулярных измерений в пунктах приема. Последнее обеспечивается за счет адаптивной пространственной обработки сигналов в каждом пункте приема и учета в алгоритме измерения угловых координат целей энергетического характера информативных параметров сигналов, принимаемых на фоне помех.

• 3.    Использование данных о параметрах сигнала позволяет повысить точность измерения информативных параметров (угловых координат) целей на фоне помех, имеющих малые угловые различия с полезным сигналом. Для использования этих данных в пунктах приема МП РЛС целесооб

• 4.    Проведен количественный анализ ошибок измерения координат целей в выбранной малобазовой МП РЛС. Установлено, что для указанного МП РЛС, СКО измерения координаты А в 1,2-1,8 раза превышают соответствующие значения СКО для двухпозиционной оптимальной когерентной обработки сигналов. Для повышения точности измерения координат цели в условиях воздействия помех предлагается использовать совместную фильтрацию оценок интенсивностей полезных сигналов и оценок их информативных параметров в пунктах приема, а также фильтрацию результатов измерения координат целей в приемных пунктах и ПОИ.

разно проводить совместную фильтрацию как угловых координат целей, так и средней энергии сигнала. Кроме того, повышение точности совместного измерения можно дополнительно обеспечить за счет формирования прогнозируемой оценки угловых координат по обьединенным данным всех пунктов при косвенном измерении [5].