Измерение пространственно-энергетических характеристик лазерного излучения с применением матричных фотоприемников

Самарский государственный аэрокосмический университет

Рассмотрены схемы измерений пространственно-энергетических характеристик лазерных пучков с использованием фоточувствительных ПЗС-матриц. Адаптации измерительных схем к широкоапертурным пучкам достигается применением рассеивающих экранов. Оценены погрешности измерений, обусловленные как характеристиками фоточувствительных ПЗС-матриц, так и формой рассеивающего экрана.

Измерение параметров излучения лазера позволяет оптимально его использовать: повысить КПД установки, добиться заданных параметров технологического или любого другого процесса, использующего лазерное излучение. Сведения о пространственноэнергетических характеристиках лазерного излучения, полученные в результате измерений, позволяют преобразовывать излучение, получаемое на выходе резонатора, в излучение с заданным распределением энергии в пространстве или на плоскости. Для этих целей можно использовать традиционные оптические элементы - линзы, либо элементы компьютерной оптики - фокусаторы или фазовые пластинки.

Для измерения пространственно-энергетических характеристик лазерных пучков [ 1 ] выгодно использовать матричные фотоприемники (МФ). МФ позволяют непосредственно получать распределение плотности мощности и энергии в сечении пучка. В случае коллимированных пучков возможны 2 схемы измерений: 1-я - МФ непосредственно совмещается с сечением пучка (рис.1), 2-я - МФ в фокальной плоскости линзы (рис.2). Оцифрованный устройством сопряжения (УС) сигнал обрабатывается ПЭВМ.

Непосредственное совмещение прием-

Рис.1. МФ совмещен с сечением пучка ной фоточувствительной площадки МФ с сечением пучка путем обработки ее сигнала в ПЭВМ реализует совместное измерение относительного распределения плотности мощности; диаметра и сечения пучка; средней мощности и нестабильности мощности. Если совместить приемную площадку МФ с фокальной плоскостью линзы, то измеряются: энергетическая расходимость и расходимость, угловая нестабильность оси диаграммы направленности (ОДН) и диаграмма направленности, а при соответствующей нормировке коэффициента оптического пропускания линзы - средняя мощность излучения и нестабильность мощности. Однако потенциальные возможности применения матричных фотоприемников в метрологии лазерного излучения практически не воплощены в серийных системах контроля лазерного излучения [2]. С другой стороны, наполнение структурных схем, представленных на рис.1 и 2, элементами массового производства делает их тиражирование вполне рентабельным. Поэто-

Рис.2. МФ в фокальной плоскости линзы му целью настоящей статьи является доказательство достижимости удовлетворительных метрологических характеристик подобных систем.

При объективной регистрации световых полей с целью измерения их пространственно-энергетических характеристик предпочтение отдается матричным твердотельным фотоприемникам, жесткий и стабильный растр которых выгодно отличает их от электроннолучевых приборов с электрической либо магнитной разверткой электронного пучка. Исходя из принятых в настоящее время физических представлений о процессах, происходящих при преобразовании "свет - электрический сигнал" в фоточувствительной ПЗС-матрице следует, что в пределах линейного участка динамического диапазона свет-сиг-нальной характеристики светочувствительного элемента накопленный в нем за время накопления электрический заряд, преобразованный в выходное напряжение в узле считывания, пропорционален количеству падающих на него фотонов

U = k . n . , (1) где U . - сигнал (выходное напряжение) с фо-точувствительного элемента матрицы, расположенного в i- ой строке и j -ом столбце; k . - коэффициент преобразования элемента (i,j) ; n .j - количество фотонов, попавших на элемент (i,j) за время накопления.

В предположении, что процедура измерения включает в себя вычитание фонового сигнала, примем условие нормировки, то есть

0 < Uti< 1, (2) и обозначим максимальную по всем фоточувствительным элементам погрешность измерения числа фотонов, падающих на фоточув-ствительный элемент и приведенную к нормированному напряжению на выходе узла считывания, о. При такой трактовке о включает в себя составляющие, обусловленные как собственно процессами преобразования "свет-сигнал" и неравномерностью чувствительности по фоточувствительным элементам в фоточувствительной матрице, так и процессами оцифровки аналогового сигнала и вычитания фонового сигнала.

Выделяют три составляющих этой погрешности: о _ст - статистическую, обусловленную процессами генерации информационных носителей заряда в фоточувствительном элементе; о _нг - неоднородностей, "вмороженных" в фоточувствительную площадку ПЗС-матрицы (геометрический шум); о _АЦП - аналого-цифрового преобразования, связь которой с о задается равенствами:

^О = V °2_т + ° 2 + °^ . ⁽³⁾

Статистическую составляющую погрешности можно оценить по такому паспортному параметру, как динамический диапазон ПЗС-матрицы, который составляет не менее, чем 1:2000, то есть О _ст =0,5 - 10^-3[3]. Погрешность аналого-цифрового преобразования для систем оцифровки и ввода изображений не превышает 10^-2 от максимального выходного сигнала телекамеры на фоточувствительной ПЗС-матрице [4], то есть о ^ _ЦП < 10^-2. Геометрический шум о _нг, который характеризуется неравномерностью выходного сигнала, может достигать ~7% [3], то есть о _нг < 10^-1.

Из приведенных числовых оценок видно, что основной вклад в погрешность измерений энергии лучистого потока одним фоточувствительным элементом вносит геометрический шум, и величина этой погрешности оценивается значением 0,1. Если по условиям применения прибора такое значение погрешности измерения энергии лучистого потока одним фоточувствительным элементом не приводит к выходу за пределы допустимых значений погрешности измерения мощности лазерного пучка, его энергетической расходимости и нестабильности положения оси диаграммы направленности, то значение о = 0,1 и следует использовать для оценки погрешностей измеряемых параметров. В противном случае необходимо включать подпрограмму выравнивания чувстви-тельностей фоточувствительных элементов, что позволяет при стендовой паспортизации параметров матричного фотоприемного устройства снизить вклад погрешности о _нг на порядок [5].

Альтернативой программным методам выравнивания чувствительности является применение высокооднородных фоточув-ствительных ПЗС на барьерах Шоттки, неоднородность которых не превышает 2% [6]. Таким образом, при оценках погрешностей измерений параметров лазерных пучков можно использовать числовые значения о , принадлежащие отрезку [0,02; 0,1].

Вторым условием, которое предполагается выполненным при проведении измерений, является согласование спектра пространственных частот, разрешаемых матричным фотоприемным устройством

2п 2п to = —; to = —, хпр. мах Ах " упр. мах а где Ах и Ау - период расположения фоточув-ствительных элементов по осям х и у ПЗС-матрицы, с максимальной пространственной частотой распределения плотности мощности или энергии в поперечном сечении лазерНого пучка Ч лп. мах и ^у лп. мах [7]:

^^х лп. мах ^х пр. мах ; ^у лп. мах ^у пр. мах* ^)

Наряду с геометрическим фактором на высокочастотный завал частотно-контрастной характеристики ПЗС-матрицы оказывают дополнительное влияние неэффективность переноса и боковое диффузное растекание зарядов в соседние ячейки [8]. Однако теоретическая оценка их вклада в частотноконтрастную характеристику требует привлечение параметров материала, из которого изготовлена ПЗС-матрица и каковые не являются паспортными (приводимыми в сопроводительной технической документации) собственно для фоточувствительных ПЗС-матриц* Более того, этот вопрос относительно просто решается экспериментально путем усиления неравенств (4).

Измерение полной энергии E или мощности P лазерного пучка матричным фотоприемником в качестве фотопреобразователя сводится, по сути, к суммированию отсчетов U.. и умножению полученной суммы на некоторый нормирующий множитель, числовое значение которого обычно получают в результате поверки. Относительная погреш ность нормирующего множителя при использовании рабочих эталонов единиц средней мощности лазерного излучения не превышает 0,5-10-2 и может быть доведена на современном уровне развития средств измерения мощности лазерного излучения до 0,15-10-2 [9]. Поэтому достаточно произвести оценку погрешности суммы

N

^U = У ' ,            (5)

• i ,    j = 1

принимая для упрощения выкладок, что матрица содержит одинаковое число фоточувствительных элементов N как по строкам, так и по столбцам.

Тогда абсолютная погрешность измерения суммы будет

PN

^AU = _а^^А Р ² = ^No ,      (6)

• V i , j = 1

а относительная составит

AU _ No _ I °П при U < No

U    U   I ^U              .    (7)

^{U   U}   [ o npuU >  No

При U >  N o относительная погрешность измерения суммы, а, следовательно, и мощности лазерного пучка будет равна погрешности ее измерения одним фоточувствитель-ным элементом, которая в данном случае выступает в роли основной погрешности прибора.

В результате получаем следующие числовые оценки относительной погрешности измерения мощности лазерного пучка без ослабителей: от 2 - 10^-2 до 20 - 10^-2. Верхняя оценка 20 - 10^-2 согласно ГОСТ 8.275-91 [9], с одной стороны, еще позволяет использовать разрабатываемую измерительную систему в качестве рабочего средства измерения, а, с другой стороны, определяет наименьшее значение измеряемой мощности.

Измерение энергетической расходимости и нестабильности оси диаграммы направленности проводится при установке фоточув-ствительного слоя ПЗС-матрицы в фокальной плоскости линзы. Фокусное расстояние линзы f является одним из параметров косвенных измерений, значение которого ис- пользуется при расчетах энергетической расходимости и нестабильности оси диаграммы направленности. Поэтому погрешность измерения фокусного расстояния будет давать свой вклад в результат оценки погрешности измеряемых величин. Известные методы измерения фокусных расстояний имеют следующие значения относительных погрешностей [10]: метод увеличений (0,3...0,6) 10-2; метод Аббе (0,2...0,5) 10-2 и метод угловых измерений (0,08^0,2) 10-2.

Угловые отклонения оси диаграммы направленности (нестабильности оси диаграммы направленности) по оси X вычисляются по формуле (по оси Y аналогично):

^х 1

^{- Х} 0 f

Ax x0

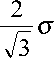
и при многоградационной обработке сигнала принадлежит интервалу (0,05; 0,5). Подстановкой (12) в (11) и принимая для оценок

Д2/3 = 1, получаем искомое выражение для оценки A6х:

A 6 _х = 2 j о .           (13)

При характерном размере фоточувстви-тельного элемента х ₀ =20 мкм [3] и фокусном расстоянии f = 100 мм без использования процедуры выравнивания чувствительности, то есть для о 10^-1, будем иметь

A6 х = 4 ■ 10-5 рад = 8 огХ.р., где X1 и х2 координаты энергетического центра фокального пятна, в моменты времени кратные периоду последовательных измерений.

Тогда абсолютная погрешность измерения угловых отклонений ОДН есть

A 6 _х

f Ax ) V 21 f J

+

^{f Х} 1 - ^Х 0

)2 f Af )2

V

f

f

7 V j 7

x i

jT^ ^f ] V x i ^- x 0

+

j TV J 7

, (9)

что согласуется с экспериментальными оценками, известными из литературных источников [12].

Погрешности измерения энергетической расходимости малорасходящихся лазерных пучков посредством матричных фотоприемников подробно рассмотрены в работе [13]. Относительная погрешность измерения энергетической расходимости ( AQ/Q J> описывается выражением:

где A x - средняя квадратичная погрешность измерения координат энергетического центра. Приняв минимально измеримое отклонение ЭЦ от своего начального положения равным погрешности измерения координат ЭЦ, то есть

A 6 6 e

If Ad )² f Af )²

+vV de 7 V j 7

где de - диаметр поперечного сечения пучка, внутри которого проходит заданная доля мощности пучка, f - фокусное расстояние линзы. ( AA de/d) оценивается соотношением:

х ₁ - х ₀ = Ах ,             (10)

получим

А 6 х

Ах С f AJ ^

2+ f f

^J * V ^{J 7}

<2Ax f

с учетом того, что Af / f < 10 ² .

Используя результаты работы [11], отношение ( A x/x 0 ), где х₀ - размер одного фото-чувствительного элемента, оценивается вы

ражением:

Ad_e / d_e = 4 о .            (15)

Поскольку ранее было показано, что 270^-2< о< 10^-1, а Af / f < 10 ^{- 2} , то из (15) и (14) видно, что основной вклад в погрешность измерения энергетической расходимости вносится погрешностью измерения диаметра фокального пятна. Сама погрешность принадлежит диапазону (8.. .40)%, которая допускается, согласно ГОСТ 26086-84 [14], при измерениях энергетической расходимости.

Для измерения характеристик излучения полупроводниковых лазеров (ППЛ) при ори-

ентации на серийные ПЗС-матрицы необходимо использовать рассеиватель. Полупроводниковые лазеры имеют большую расходимость излучения: в плоскостиp-n-перехода -5-10 ° , а в плоскости, перпендикулярной активному слою - (20-40) ° , поэтому охват всего поля их излучения приемной площадкой фоточувствительной ПЗС-матрицы представляет собой трудноразрешимую проблему.

Оценим погрешность измерения относительного распределения плотности мощности (ОРПМ) в сечении пучка, т.к. именно ОРПМ совместно с координатами энергетического центра является основой расчета остальных пространственно-энергетических характеристик лазерного пучка. Оценку произведём в рамках геометрической оптики (рис.3), предполагая, что объектив 2 преобразует элемент пространства предметов (экрана 1) dx1 в элемент пространства изображений dx , находящийся на поверхности (плоской) фоточувствительной матрицы. Кроме того, будем считать объектив идеальным, не поглощающим света и переносящим без потерь световую энергию, попавшую на входной зрачок объектива от элемента экрана dx1 на элемент изображения dx.

Форму экрана примем цилиндрической с осью цилиндра ориентированной параллельно оси y1, учитывая, что в направлении у1 диаграмма направленности узка. С одной стороны, это позволит воспользоваться про стым линеаризованным законом преобразования второго измерения излучающей площадки экрана dy1 в dy. С другой стороны, если в результате числовых оценок окажется, что в требуемом для охвата диаграммы направленности в направлении у диапазоне углов отклонение величины светового потока на фоточувствительной матрице от случая узких (параксиальных) пучков невелика, то этот факт может служить основанием для использования экрана цилиндрической формы и для достаточности одномерной модели.

Исходя из принятой геометрии измерений, отображенной на рис.3 получим формулы преобразования геометрических величин из пространства предметов в пространство изображений, используя в качестве варьируемого параметра угол а , который непосредственно характеризует диаграмму направленности ППЛ. В качестве постоянных параметров установки выступают: R- радиус кривизны экрана; 1- расстояние от экрана до объектива; а- расстояние от объектива до изображения экрана, где и устанавливается фоточув-ствительная матрица.

В силу того, что объектив должен строить действительное изображение на фоточувствительной матрице, а должно быть немного больше f (а >  f). Хотя для формальных геометрических соотношений и не важны ограничения, налагаемые на R, 1 и а, тем не менее, для реальной схемы измерения:

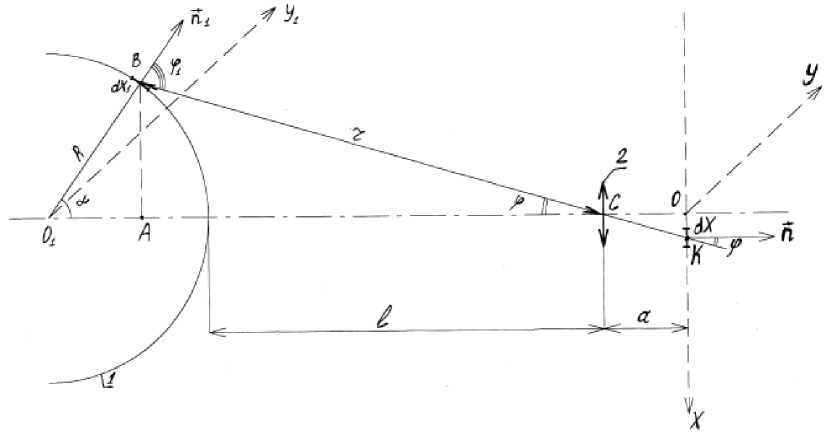
Рис.3. Геометрическая схема с рассеивателем

l > R и l >>  a.

Из геометрических соображений.

AB = R ■ sin а ; AC = 1 + R ■ (1 - cos a ) ;

AB R ■ sin a tg® =---=--------------;

AC R ■ (1 - cos a ) +1

Зависимость коэффициента пропускания линзы, обусловленную чисто геометрическим фактором - наклоном падающих лучей, излучаемых элементом dx 1 , - имеет вид:

v = m ■ cos(arctg

ϕ = arctg

R ■ sin a

R ■ (1 - cos a ) + 1

R ■ sin a )

R ■ (1 - cos a ) + 1

^ф 1

= α + ϕ = α + arctg

R ■ sin a

R ■ (1 - cos a ) + 1

где m - действующая площадь объектива.

Масштабные преобразования по оси у учитываются как:

BC = r = V AB ² + AC ² = .---------------------------2 , (18)

= RR ■ sin a + {R ■ (1 - cos a ) +1}

dy 1 = ACd_y = l + ^R ■ ⁽1 - cos a ) dy . (2₄) aa

Поток dФ, переносимый с площадки dx1dy1 на соответственную ей геометрически площадку dxdy описывается выражением:

где r - расстояние от излучающего элемента dx1 до оптического центра линзы

Пусть x(dx) - x-вая координата элемента dx. Тогда из А СОК ^ А АВС имеем:

Т cos ф ■ cos Ф , , , , dФ = L ■ v-- 2-----dx i dy i dxdy , (25)

r

, , . AB a ■ R ■ sin a x(dx) = a --=---------------- ,

AC R ■ (1 - cos a ) + 1

Находим производную:

где L - яркость площадки (dx 1 dy 1 ) экрана с координатами (x 1 , у) пропорциональная, падающему на эту площадку потоку излучения лазера.

Рассмотрим коэффициент

d- ⁽ x ⁽ dx)) = dα

J =    dΦ mL(dx)2 (dy)2

£2 ^^ k 1 k 2 k 3 , (26) r ²

a ■ R ■ cos a ■ ( R ■ (1 - cos a ) + 1) - a ■ R² ■ sin² a

(R ■ (1 - cos a ) + 1 )²

Тогда соотношение между дифференциалами d a и dx примет вид:

,                 (R ■ (1 - cos a) +1 )2                  стах da =----------— ------'—' 2 2— dx, (21)

a ■ R ■ cos a ■ (R ■ (1 - cos a) +1) - a ■ R2 ■ sin2 a которое будет приближенно выполняться и для конечных приращений, причем под dx можно подразумевать период следования фоточувствительных элементов.

Выражение (21) даёт угловое поле зрения в пространстве предметов, соответствующее периоду следования фоточувствительных элементов матричного фотоприемника, а, учитывая что dx1 = R ■ da , получаем протяженность экрана вдоль цилиндрической поверхности, соответствующую dx, в пространстве предметов:

dx , =----------- ⁽ ■'" ^{- cos a ) + 1 )2} -----------dx . (22)

a ■ cos a ■ (R ■ (1 - cos a ) + 1 ) - a ■ R ■ sin² a

зависящий от a и характеризующий влияние геометрических параметров установки на фотоотклик одного фоточувствительного элемента матричного фотоприемника. Здесь:

^k 1 =

( R ■ (1 - cos a ) + 1 )²

a ■ cos a ■ ( R ■ (1 - cos a ) + 1 ) - a ■ R ■ sin² a ’

,              , R ■ sina k. = cos( arctg------------------),

²             R ■ (1 - cos a ) + 1

. _ 1 + R ■ (1 -cos a ) k 3 =

.

a

Используя (26) удобно ввести следующие функции общего аргумента a : угловую разрешающую способность

P = d a =_____________ ( R ■ (1 - cos a ) + 1 )² _____________

• ¹    = dx = a ■ R ■ cos a ■ (R ■ (1 - cos a ) + 1) - a ■ R ² ■ sin² a’

(30) линейную разрешающую способность p _ dx1 _           (R ■ (1 - cosa) +1 )2

• ²    = "dx = a ■ cos a ■ ( R ■ (1 - cos a ) + 1 ) - a ■ R ■ sin² a"

угловое поле зрения при заданных размерах фотоприёмной матрицы w = 2Xmax(dx) ,           (32)

линейную разрешающую способность по направлению оси у в пространстве предметов р _ dy1 _ l + R" (1 - cos«)

³ dy          a

•

В качестве примера на рис. 4 приведен график зависимости (30).

Оценки величин, входящих в (26), т.е. еаз фф , еаз фф ₁, r, k₁, k₂, k₃ и самого коэффициента J при варьировании а от 0^о до 10^о для характерных размеров установки R = 60 мм, a = 25 мм, l = 200 мм показывают, что их изменение не превышает 10% от значения, соответствующего а = 0^о. Это указывает на правомерность применения одномерной модели для случая, когда диаграмма направленности излучения в некоторой плоскости принадлежит области углов, не превышающих 20^о.

Из рисунка 4 видно, что при а <40⁰ (т.е. расходимость менее 80⁰) погрешность измерения лазерных параметров, обусловленных формой экрана и геометрией установки составляет менее 20%. Для уменьшения погрешности следует проводить коррекцию результатов измерений в соответствии с выражением (26).

Таким образом, применение МФ с ПЗС-матрицами в качестве датчиков в системах для измерения параметров лазерного излучения способно обеспечить метрологические характеристики, удовлетворяющие существу-

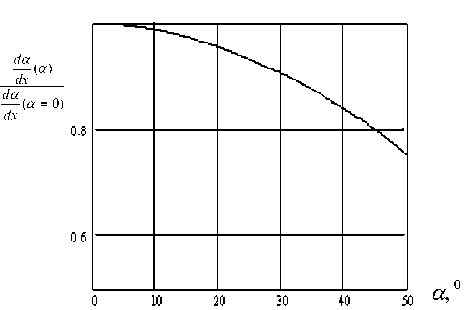
Рис.4. График зависимости угловой разрешающей способности ющим нормативным документам. Их совместное использование с современными средствами вычислительной техники при соответствующем программном обеспечении позволяет создавать автоматизированные системы измерений.