Измерение радиуса кривизны сферической поверхности на основе уравнения переноса интенсивности

С развитием когерентных источников света и вычислительных методов синтеза волновых полей широкое распространение получили оптические методы обработки информации. Развитие этих методов сопровождалось значительным улучшением средств регистрации и элементов оптических систем, обеспечивающих преобразование сигналов с высокой точностью в режиме реального времени. В связи с этим в приложениях оптической метрологии традиционная оценка распределений интенсивности и фазы лучей, распространяющихся через систему, на основе явления интерференции и геометрической оптики перестала удовлетворять практическим нуждам оптимизации оптических систем. Поэтому актуальна проблема анализа систем с высоким разрешением в режиме реального времени на основе свойств оптических сигналов [1–4].

Существующие подходы к решению задачи регистрации и восстановления амплитудно-фазовой информации, впервые сформулированные Вольфом [5] и Уокером [6], основаны на анализе аналитических свойств функций, описывающих оптические сигналы

и поля. Например, в [7] по зарегистрированным ди-фрактограммам визуализируют интенсивность и фазу образца ленточного червя с использованием различных длин волн и частичного временного и пространственного когерентного освещения. Авторы [8] предложили метод, позволяющий восстанавливать фазовый профиль сложных оптических поверхностей. Также известен ряд методов на основе уравнения переноса интенсивности с его решением через различные преобразования, в том числе Фурье [9, 10], Гилберта [11], косинусное [12] и др. [13– 16], выбор каждого из которых зависит от условий и ограничений решаемой задачи. Кроме того, известна работа [17], где на основе дисперсионных соотношений Крамер-са–Кронига реализована неинтерферометрическая голографическая визуализация изображений тонких объектов в различных спектральных режимах. Однако анализ литературы показал, что до сих пор существует ряд проблем как научного, так и технического характера, которые не позволяют использовать разработанные методы для решений задач оптической метрологии [18]. Ведь несмотря на простоту их реализации, они все же достаточно медленны и трудоемки [8, 19]. Более того, все эти методы предъявляют высокие требования на пространственно-временные параметры импульсного или непрерывного лазерного излучения [20].

В данной работе впервые предлагается простой метод абсолютного измерения радиуса кривизны сферической поверхности на основе решения уравнения переноса интенсивности с использованием только одной камеры. Радиус кривизны является важным параметром любой оптической детали, от которого, например, зависит смещение каустики – геометрического места всех фокусов негомоцентрических пучков, то есть пучков световых лучей, не сходящихся в одной точке. Поэтому решение задачи, полученное в данном исследовании, позволит ускорить практическую реализацию с помощью одной КМОП-камеры тех больших потенциальных возможностей, которые заложены в предлагаемом методе. Ведь не потребуется высококачественных и дорогих объективов и эталонов, существенно снизится влияние вибраций и температурных колебаний окружающей среды на показания измерений, будет отсутствовать зависимость контраста и яркости восстановленного поля от монохроматичности источника и его протяженности.

где z R – длина Рэлея лазерного пучка, т.е. расстояние от перетяжки пучка до точки, в которой размер пучка увеличивается в √2 раз.

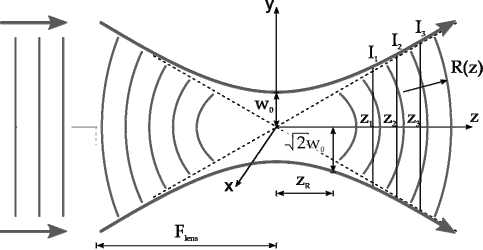
Рис. 1. Пространственная структура лазерного пучка

1. Базовые принципы

Метод по абсолютному измерению радиуса кривизны сферической поверхности основан на регистрации распределений интенсивности излучения в нескольких поперечных сечениях пучка. Поэтому рассмотрим процесс распространения лазерного излучения через плоско-выпуклую линзу, расположенную в воздушной среде. Предположим, что на линзу падает пучок с Гауссовым профилем распределения интенсивности. Тогда для описания комплексной амплитуды поля необходимо решить уравнение Гельмгольца в параксиальном приближении [21]. При этом радиальное распределение интенсивности I ( r , z ) такого пучка будет определяться как [22]:

В связи с этим в продольном направлении лазерный пучок можно разбить на три части. В центральной части при | z | <  z_R поперечные размеры пучка сравнительно мало меняются с изменением z , а значение радиуса волнового фронта в этой области будет стремиться R ( z )⟶ ∞ согласно [23]. В двух же периферийных частях (при z <– z R и z >  z R ) поперечные размеры пучка существенно увеличиваются с ростом z и при больших z пропорциональны | z |, а радиус волнового фронта принимает значения согласно следующей формуле:

R ( z ) - z + — .

z

Пространственные параметры лазерного пучка, характеризующие продольное сечение распределения интенсивности, взаимно-однозначно связаны с оптическими характеристиками линзы [24]:

M2 -X-Fens wз  --------;---- л-d

,

I ( г , z ) -

E ( r , z ) ²

2П

- 1 0

H Q | w (z ) J

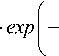
r ² )

w ⁽ z ⁾² J ’

где r = (x, y) – радиус-вектор; z – продольная координата; E ( r , z ) – комплексная амплитуда электрического поля; η – волновое сопротивление среды; I 0 – интенсивность в центре перетяжки лазерного пучка; w (z) – радиус лазерного пучка; w 0 – радиус перетяжки.

Рассмотрим теперь лазерный пучок, прошедший через плоско-выпуклую линзу. Продольное сечение осесимметричного лазерного пучка, распространяющего вдоль оси z , представлено на рис. 1. Огибающая w ( z ) осесимметричного лазерного пучка по уровню 1/e² полного потока является однополостным гиперболоидом вращения:

w ( z ) - w ₀

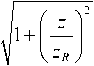
где d – диаметр пучка по уровню 1/e²; λ – длина волны излучения; F lens – фокусное расстояние линзы; M ² – параметр качества пучка. Следовательно, из формулы (4) можно определить параметры линзы:

F, = lens

w0 - л - d m 2-X .

Если из (2) выразить w 0 и представить значение длины Рэлея z R через радиус волнового фронта (3), то, подставляя их в (5), можно получить выражение вида:

F = lens

л- d - w ( z )

M2-X- 1 + —z— R (z) - z

В свою очередь, радиус кривизны волнового фронта может быть рассчитан с помощью уравнения переноса интенсивности, в котором фазовая функция поля ф ( r, z ) связана с распределением интенсивности I ( r , z ) следующим соотношением [25]:

I                                                                                                                                                     I

Ф( r, z) - k • V-2 ^ V • ^ -^— VV-2 ° I (rr’ z) I I, I [ I (r, z)            °zI

где V = { д /5 x ; д/дy } - оператор градиента; V ^-2 - оператор обратного Лапласиана. Одним из наиболее универсальных методов расчета дифференциальных операторов градиента и обратного Лапласиана является метод, основанный на свойствах преобразования Фурье [26].

Полученную с использованием формулы (7) фазовую функцию φ ( r, z ) и измеренный радиус лазерного пучка w ( z ) можно использовать для расчета радиуса волнового фронта R ( z 2 ) в плоскости z 2 с использованием геометрического метода [27]

R ( z ) - 7 + _F ,                                (8)

28s где s – стрелка прогиба, которая рассчитывается на основе фазовой функции φ (r, z2) (см. [27]); l = w(z2).

Стоит отметить, что данный подход подразумевает регистрацию нескольких распределений интенсивности I ( r , z 1 ) и I ( r , z 3 ) в различных плоскостях, а получаемое значение фазовой функции поля φ ( r, z 2 ) восстанавливается в промежуточной плоскости z 2 , равноудаленной от плоскостей z 1 и z 3 . Алгоритм расчета фазовой функции представлен на рис. 2.

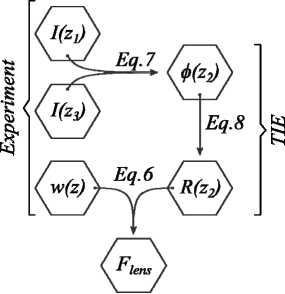
Рис. 2. Алгоритм расчета параметров линзы

Апробация предложенного метода осуществлялась с использованием фемтосекундного лазера Satsuma с длиной волны второй гармоники X SH =515,6 нм. При этом на выходе из лазера пучок имеет размеры 1,627 мм и 1,576 мм. Для обеспечения малой угловой расходимости падающего на линзу пучка в схему была установлена телескопическая система Кеплера (линза Л1 и Л2), которая коллимировала лазерный пучок и расширяла его до диаметра 3,4 мм по уровню 1 ∕e². Эквивалентная схема эксперимента представлена на рис. 3.

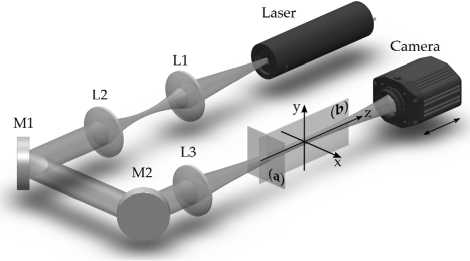
Рис. 3. Экспериментальная схема, состоящая из лазера, телескопической системы (линза Л1 и Л2), исследуемой линзы Л3 и КМОП-камеры

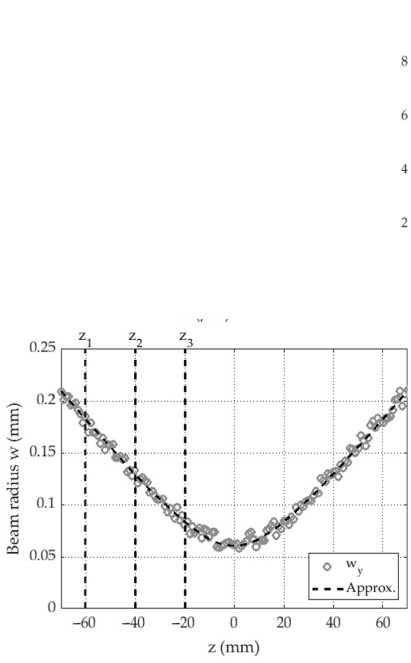
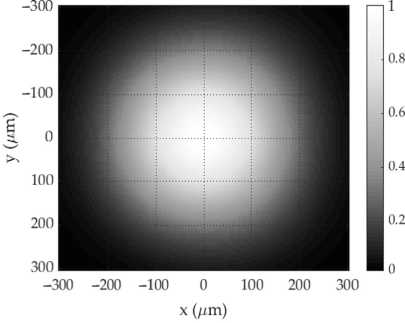
Преобразованное исследуемой линзой Л3 излучение регистрировалось монохромной КМОП-камерой (разрешение 1920×1080 c размером пикселей 5,04×5,04 мкм²), которая перемещалась вдоль оси распространения излучения на линейном трансляторе. Поперечное распределение интенсивности регистрировалось в области перетяжки излучения с шагом 1 мм. На рис. 4 а представлено поперечное сечение пучка в произвольно выбранной плоскости X0Y ( z =– 60 мм относительно плоскости перетяжки, плоскость (a) на рис. 3). На основе подобных распределений интенсивности было восстановлено продольное сечение осесимметричного лазерного луча в плоскости Y0Z (плоскость (b) на рис. 3) по уровню 1 ∕ e ² (рис. 4 б ).

Представленное на рис. 4 б продольное сечение есть не что иное, как гиперболическая зависимость радиуса лазерного пучка от продольной координаты z , которую можно аппроксимировать и записать как w ( z ) - a а + bz + cz ² [28]. Расчет коэффициентов a , b , c обычно производится с использованием метода наименьших квадратов, используя при этом матричное выражение согласно [29]. Расчет коэффициентов показал, что а = 0,059 мм², b =-1,458 - 10^-3 мм и c = 9,506 - 10 ^-6.

При этом эти коэффициенты имеют взаимнооднозначную связь с пространственными параметрами лазерного пучка, а именно [29]: радиус перетяжки w0 - У 4ас -b2 /2c,длина Рэлея лазерного пучка zR - У4ас — b2 / 2с, угловая расходимость 20 - 2Ус и положение перетяжки луча относительно выбранной базовой плоскости Sp =– b/2c. Из представленного перечня наиболее интересующим нас параметром яв- ляется длина Рэлея лазерного пучка zR, так как этот параметр фигурирует в формулах (2) и (3). Расчет показал, что для данной конфигурации экспериментальной схемы длина Рэлея лазерного пучка составила zR = 21,785 мм.

а)

б)

Рис. 4. (а) Поперечное распределение интенсивности пучка, (б) продольное сечение распределения интенсивности

ментальных данных с целью определения оптимального значения д z . Полученные значения фазы ф ( r i , z₂) в промежуточной плоскости z 2 в дальнейшем использовались в формуле (8) для расчета радиуса кривизны волнового фронта R ( z 2 ).

На рис. 5 представлены некоторые из полученных результатов расчета радиуса кривизны волнового фронта R ( z 2 ) для различных д z . Точками обозначены экспериментальные значения радиуса кривизны волнового фронта R ( z ), а сплошными линиями обозначены их аппроксимационные функции. Пунктирной линией обозначена теоретическая зависимость R ( z ), которая была получена с использованием уравнения (3) при z_R = 21,785 мм. Из рис. 5 видно, что для д z = 30 мм аппроксимированная по экспериментальным данным кривая совпала с теоретической зависимостью R ( z ).

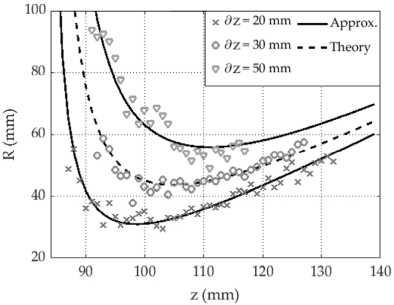
Рис. 5. Зависимость радиуса кривизны R(z 2 ) от продольной координаты для нескольких д z

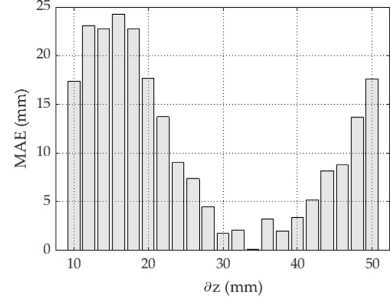
Рис. 6. Зависимость средней абсолютной ошибки от величины д z

При расчете продольной производной величина д z изменялась в диапазоне от 10 до 50 мм с шагом в 2 мм. В качестве оценочного параметра была выбрана средняя абсолютная ошибка (MAE) [30] между теоретической функцией радиуса кривизны волнового фронта R ( z ) и экспериментальными данными в зависимости от д z . На рис. 6 представлены численные значения MAE, из которых можно увидеть, что минимальная ошибка была получена при д z = 32 мм.

На завершающем этапе, используя рассчитанные значения радиуса кривизны волнового фронта R ( z )

при Э z = 32 мм и полученные значения радиуса лазерного пучка w ( z ), можно определить фокусное расстояние линзы F lens . На рис. 7 приведена гистограмма полученных значений. Анализ гистограммы показал, что распределение может быть аппроксимировано функцией Гаусса, при этом математическое ожидание аппроксимированной функции в данном случае составило ц = 539,8 мм, а дисперсия а = 0,042 мм.

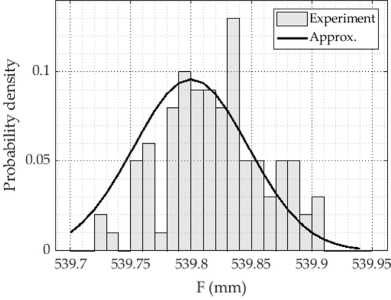
Рис. 7. Плотность вероятности экспериментальных значений

Согласно [31], существует взаимно-однозначная связь между фокусным расстоянием плосковыпуклой линзы, радиусом кривизны оптической поверхности и показателем преломления:

R lens = (~ " I) • F ens . n 0

Из данного уравнения следует, что для расчета радиуса кривизны оптической поверхности требуется знание априорной информации о показателе преломления на рабочей длине волны лазерного излучения. Если принять искомое значение фокусного расстояния за F lens = 539,8 мм (значение математического ожидания нормального распределения на рис. 7), а значение показателя преломления за n х =1,5205, то радиус кривизны сферической поверхности будет равен R_lens = 280,9443 ± 0,0314 мм. Стоит отметить, что соотношение (7) было получено с допущением о справедливости параксиального приближения. Это накладывает определенное ограничение, в силу которого минимальное значение радиуса кривизны волнового фронта, при котором точность предлагаемого метода будет сохраняться, составляет около 40 мм [27].

Несмотря на вышеупомянутое ограничение, данный метод можно использовать и для оценки значения показателя преломления оптической линзы [4]. При этом алгоритм расчёта остается неизменным вплоть до последнего этапа, а для определения значения показателя преломления необходима априорная информация о радиусе кривизны сферической поверхности. Еще следует отметить, что в данной работе мы исследовали работоспособность нашего метода с использованием одномодового одночастотного лазера с параметром M ², близким к 1,0.

Заключение

В работе представлен простой метод для задач оптической метрологии, позволяющий прецизионно контролировать радиус кривизны сферических поверхностей бесконтактным способом на основе решения уравнения переноса интенсивности. Абсолютное значение радиуса кривизны восстанавливается из зарегистрированных на одной КМОП-камере распределений интенсивности, также предложенный метод не требует использования сложных оптических систем. Апробация была проведена на плоско-выпуклой линзе с радиусом кривизны R lens = 280,954 мм, предха-рактеризованной на интерферометре с точностью λ /20. Сравнение полученных результатов показало различие на уровне A R_lens = 0,01 мм, что говорит о хорошем согласовании. Преимуществами предложенного подхода являются экспериментальная простота реализации и универсальность из-за инвариантности к материалу исследуемых элементов. Более того, после небольшой модификации схемы метод может быть использован и для контроля радиуса кривизны поверхностей оптических элементов в процессе их производства.

Работа выполнена при поддержке Российского научного фонта (проект №20-79-00264) и Российского Фонда Фундаментальных Исследований (проект № 20-32-90161).