Измерение разности фаз сигналов в системах спутниковой связи с использованием одного геостационарного ИСЗ

Решение многих задач радиотехники опирается на измерение фазового сдвига (ФС) двух сигналов. Фазовые соотношения используются в космической навигации для определения дальности до космических аппаратов (КА), координат КА, а также в радиопеленгации для определения координат источника радиоизлучения на поверхности Земли при помощи искусственных спутников [1 - 3].

Развитие радиоэлектронных компонентов и радиоэлектронных средств стимулирует развитие фазоизмерительной техники, повышая требования к точности измерений. В то же время развитие радиотехнических систем приводит к необходимости создания более совершенной измерительной аппаратуры и метрологической базы. Все это требует опережающего развития фазоизмерительной техники.

Существует множество методов измерения разности фаз сигналов, возьмём один из описанных в [4–6] и промоделируем.

Разработанная и исследуемая модель цифрового измерителя разности фаз представляет собой устройство, показанное на рис. 1.

Устройство имеет два входа. На вход 1 подается синусоидальное напряжение с известной частотой и неизвестной начальной фазой. Аналоговый сигнал S ( t ) оцифровывается на аналого-цифровом преобразователе с частотой выборки, задающейся частотой кварцевого генератора. Блок измерения периода осуществляет измерение периода входного аналогового сигнала S ( t ) методом дискретного счета. Сигнал с перестраиваемого по частоте опорного генератора ОГ проходит на опорный вход измерителя - вход 2 и направляется напрямую на блок цифровой обработки (подстройка ОГ может производиться точно под частоту аналогового сигнала при однополупериодном

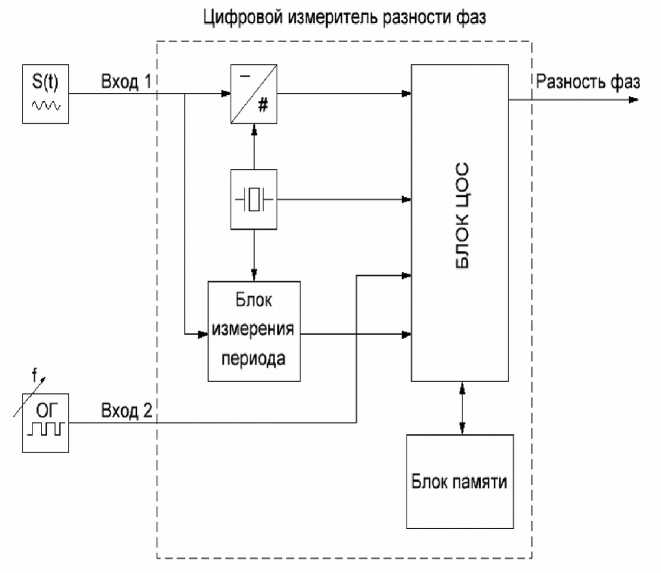
Рис. 1. Исследуемое устройство

измерении или под удвоенную частоту аналогового сигнала при двухполупериодном измерении). Классическая схема реализации данного фазоме-

тра подразумевает наличие опорного и измеряемого сигналов на обоих входах измерительного

Значение t ф можно определить измерив координаты перехода аналогового сигнала через нулевой уровень «снизу-вверх» или «сверху-вниз» (рис. 1). Тогда:

устройства.

Разность фаз двух сигналов рассчитывается согласно следующему выражению [4]:

t ф ^_ t 1 ^- t 2 ,                   (3)

360°-^

т

где t ф - временной сдвиг сигналов; Т - период сигнала.

Теперь определим величину погрешности измерения фазового сдвига, определяющуюся двумя компонентами: погрешностью измерения величины t ф - временного сдвига сигналов и погрешностью измерения периода сигнала как погрешностью косвенных измерений [7]. Для погрешности измерения ФС будем иметь следующее выражение:

где t ₁ – координата перехода через ноль (например, снизу-вверх) измеряемого сигнала; 1 ₂ - координата времени по заднему или переднему фронту импульса ОГ.

Исходя из формул (1) и (3), для разности фаз

получим выражение

360°-(^i-^)

С учетом формулы (4) формула (2) видоизменится, и для вычисления погрешности измерения фазового сдвига получим уже несколько иную формулу:

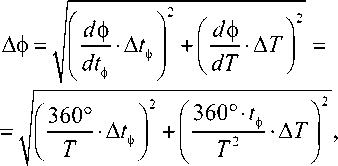
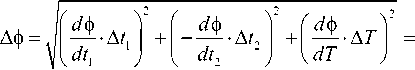
(360°-A?, Y ------- +

( Т )

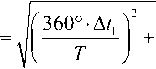
(5) v т ;

где A t ф - абсолютная погрешность измерения временного сдвига сигналов; A T - абсолютная погрешность измерения периода сигнала.

где Δ t ₁ – абсолютная погрешность координаты перехода через ноль измеряемого сигнала; A 1 ₂ -абсолютная погрешность координаты времени по заднему или переднему фронту импульса опорного генератора.

Havko____________

Ж ГРАДА

Величины A 1 1 , A T зависят от построения модели и в данном случае определяются периодом дискретизации, так как АЦП и блок измерения периода тактируются одним высокостабильным кварцевым генератором. Величина A 1 ₂ определяется периодом сигнала и абсолютной нестабильностью частоты Δ f опорного генератора.

Реально достижимые величины частот дискретизации АЦП, выпускаемых компанией Analog Devices Inc для высокоскоростных АЦП, лежат в пределах до 1-2 ГГц [8]. Выбор частоты дискретизации определяется частотой входного сигнала.

32 Для грубого определения разности фаз необходимо, чтобы частота дискретизации превышала частоту сигнала в 500 раз и более [1]. Абсолютная нестабильность частоты высокостабильных генераторов фирмы Epson может достигать 20–30 Гц при синтезируемых частотах порядка десятков МГц [9].

Для построения графиков зависимости погрешности измерения разности фаз от возможных источников погрешностей по умолчанию были выбраны:

• 1)    измеряемая задержка t _ɸ = 1 нс;

• 2)    период дискретизации, определяющий величины Δ t ₁, Δ T , равный 500 Мгц;

• 3)    нестабильность частоты опорного генератора, определяющая величину A 1 ₂, равную A f = 20 Гц;

• 4)    частота сигнала, заданная на уровне 1 МГц, что в 500 раз ниже частоты дискретизации.

Кроме того, при моделировании не учитывались шумы и использовался один период колебания для измерения.

В результате расчетов в системе MATLAB были построены графики зависимости погрешности измерения разности фаз от значений абсолютных отклонений величин, входящих в формулу (5).

Том 1

Анализ данного графика (рис. 2) четко показывает, что при выбранных константных параметрах, описанных выше, величина измеряемой задержки начинает вносить заметный вклад при приближении её к величине порядка 100 нс. То есть при величинах измеряемой задержки, меньших 100 нс, величина погрешности, вносимая компонентой t _ф, почти не влияет на результирующую погрешность.

Существенное влияние, во многом определяющее погрешность измерения разности фаз, вносит выбор частоты дискретизации и частоты сигнала. Зависимость погрешности измерения разности фаз от выбора периода сигнала при частоте дискретизации 500 МГц показана на рис. 3. График зависимости погрешности измерения разности фаз от величины, обратной частоте дискретизации при частоте сигнала 1 МГц, приведен на рис. 4. На графиках видно, что при увеличении периода сигнала при постоянном значении частоты дискретизации погрешность измерения разности фаз падает. При уменьшении же частоты дискретизации погрешность измерения разности фаз падает.

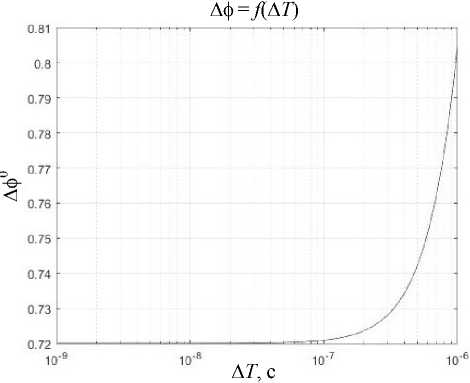
Рассматривая график, показанный на рис. 5, можно сделать вывод о том, что помимо выбора частоты сигнала и частоты дискретизации следует соблюсти необходимую точность при измерении периода сигнала, так как при точности измерения менее семи знаков после запятой наблюдается заметный рост результирующей погрешности (при прочих константных параметрах).

В целях большей информативности построим график Aф = g (A f ) при условии того, что A 1 ₂ = h (A f ). Погрешность измерения разности фаз при увеличении абсолютной нестабильности частоты опорного генератора растет, но для того,

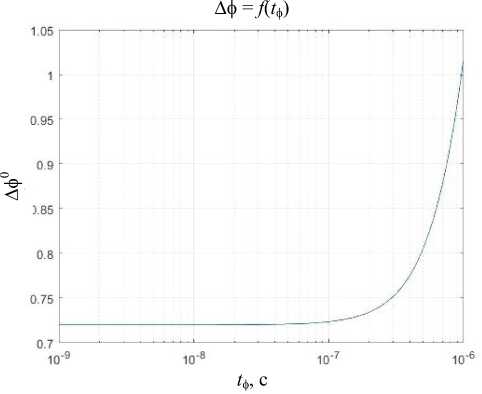
Рис. 2. График зависимости погрешности измерения разности фаз от величины измеряемой задержки

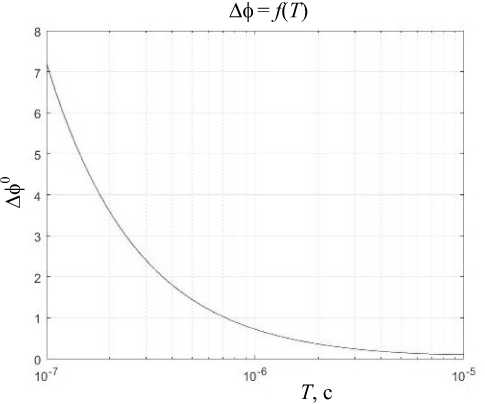
Рис. 3. График зависимости погрешности измерения фазы от периода сигнала

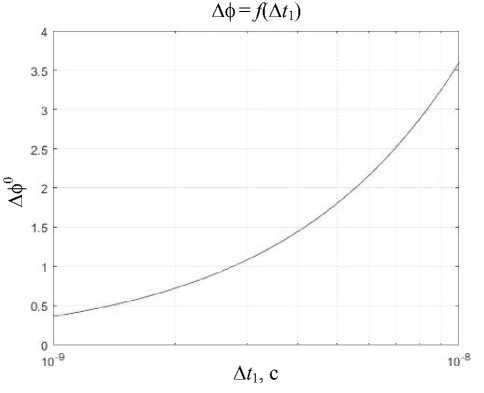
Рис. 4. График зависимости погрешности измерения фазы от погрешности координаты перехода через ноль измеряемого сигнала

Δφ = f ( Δ T )

0.81

0.3

0.79

0.78

0.77

0.73

0.75

0.74

0.73

0.72

ю-9

10 л т 10'

Δ T , с

Рис. 5. График зависимости погрешности измерения фазы от погрешности измерения периода сигнала

чтобы она сравнялась с погрешностью, вносимой выбором частоты сигнала или частоты дискретизации, необходимо, чтобы нестабильность частоты опорного генератора достигала 1000 Гц. При абсолютной нестабильности частоты 1000 Гц и частоте сигнала 1 МГц относительная нестабильность частоты такого генератора будет равняться 0,1 %, в то время как относительная нестабильность частоты генераторов прилично ниже и измеряется 10-4—10-5 %.

Исследуя полученные графики зависимости погрешности измерения разности фаз от различных параметров, входящих в формулу (5), можно сказать, что определяющее влияние на погрешность измерения ФС в данной модели оказывает выбор частоты дискретизации и периода измеряемого сигнала. Влияние величины измеряемой задержки t _ɸ несущественно при измерении времени задержки менее 100 нс. Влияние погрешности измерения периода Т пренебрежимо мало при измерении периода с точностью более семи цифр после запятой. Нестабильность частоты опорного генератора вносит незначительный вклад в погрешность измерения разности фаз, если ее порядок 10^–6–10^–7.

Рассмотрим описанный выше измеритель разности фаз применительно к ситуации, когда опорный сигнал и сигнал с измеряемой фазой поступают на вход измерителя разновременно. На практике данную задачу необходимо решать при определении координат земной спутниковой станции, используя при этом только один геостационарный спутник [4, 6, 9]. Опорный и измеряемый сигналы в данном случае принимаются разновременно и в течение определенного заданного промежутка времени.

При такой реализации измерения разности фаз функциональная схема будет выглядеть согласно рис. 7.

Сигнал, пришедший в момент времени t ʹ, оцифровывается и запоминается в памяти. Далее, когда в момент времени t " на вход фазометра поступает сигнал от того же источника с неизвестной частотой и фазой, отсчеты сигнала, оцифрованного ранее, выступают в роли опорного сигнала. Измерение разности фаз в данном случае происходит в цифровой форме. Сдвиг сигнала по фазе осуществляется в аналоговой форме перед оцифровкой. Фазовый сдвиг будет определяться похожим с (4) выражением

Δφ = f ( Δ f )

0.745

0.735

0.725

>.72‘:Ч“»*^ЙЧ^?®?^^—¹ =— ^i™—¹   и ¹ С У ^

О 50   100   150   200   250   300   350   400   450   500

Δ f , Гц

Рис. 6. График зависимости результирующей погрешности измерения разности фаз от нестабильности частоты опорного генератора

Havko____________

>ГРАДА

± 360° •(?,'-//') 360o-Z,' 360°-Z/

ф=—..       ...—(6)

где T 1 - период сигнала, принятого в момент времени 1 '; T ₂ - период сигнала, принятого в момент времени t ʹʹ; t ʹ – координата перехода через ноль сигнала, принятого в момент времени 1 '; 1" - координата перехода через ноль сигнала, принятого в момент времени t ʹʹ. Однако погрешность в данном случае будет иметь уже несколько другое выражение в связи с разновременным приемом сигналов:

Аф = J —-ДА * + —-АГ +         =

V U,                      kdT, ' \<Щ -

Том 1

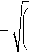
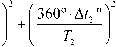
збО’ч.'-дт:

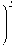
Г 360° -л "-at; У

I ^Ti )

Цифровой измеритель разности фаз

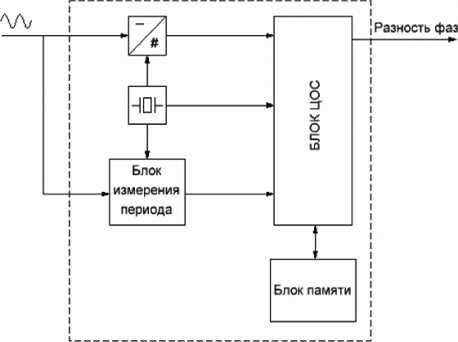
Рис. 7. Цифровой измеритель разности фаз при разновременном приеме сигналов

В данном случае величины A 1 1 ' и A 1 ₂'' являются абсолютными погрешностями измерения времени перехода через ноль первого и второго сигналов, принятых разновременно.

^В формуле ⁷ появляются величины 1 1 ' и ¹ 2 '' вместо величины 1 _ф, которые определяются согласно выражениям (8) и (9):

ti ‘ = t' +131 +                        (8)

T2

t2 = t + tсп + tЗ2 + ^ ,               (9)

где 1 _СП - время передвижения спутника, 1 ₃₁ и 1 ₃₂ -время распространения сигналов от спутника к станции.

В рамках проведения измерений можно будет искусственно занулить 1 1 ', исключая все известные задержки (время движения спутника, аппаратные задержки и др.), и, полагая, что периоды обоих сигналов равны T 1 = T ₂ = T , по аналогии с (4) 1 ф ' будет равно времени 1 2 ’, т.е. времени смещения одного сигнала относительно другого из-за прохождения сигналами разных расстояний ввиду смещения спутника на орбите. В связи с таким подходом формула (7) примет следующий вид:

По результатам исследования можно сделать следующие выводы: при применении современных радиотехнических средств возможно измерять разность фаз сигналов, принятых разновременно в фиксированные промежутки времени от одного источника радиоизлучения с определенными ограничениями. При реализации данного способа измерения разности фаз сигналов следует обращать пристальное внимание на выбор частоты дискретизации, превышающей частоту сигнала в 500 раз и более. Помимо этого необходимо предъявлять особые требования к точности измерения периодов принимаемых сигналов (точность измерения должна достигать 7 и более знаков после запятой). Также весомое влияние на погрешность измерения разности фаз оказывают большие измеряемые времена задержки. Минимизация погрешности, вносимой дан-

р60°-АЛ') <360°-А^п) ГзбО°-<-АТ?) /лгхх

^АФ = л -----^L + ------ + ----1—- (10)

Отличие данной формулы (10) от формулы (5) состоит в том, что величина A 1 ₂'' в отличие от величины A 1 ₂ из формулы (5) зависит от периода дискретизации t ₀, т.е. ошибка измерения времени перехода через ноль опорного сигнала становится намного больше, нежели для схемы с опорным генератором (рис. 1).

Для данной схемы построим графики зависимостей погрешности измерения разности фаз от величин, входящих в формулу (10), при выборе тех же константных параметров частоты дискретизации, периода сигнала и измеряемой задержки.

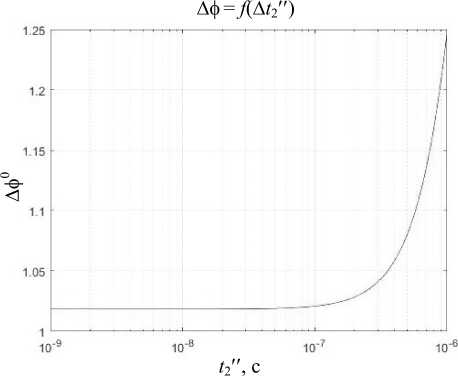
Рис. 8. График зависимости погрешности измерения разности фаз от измеряемой задержки при разновременном приеме сигналов

Аф = f T)

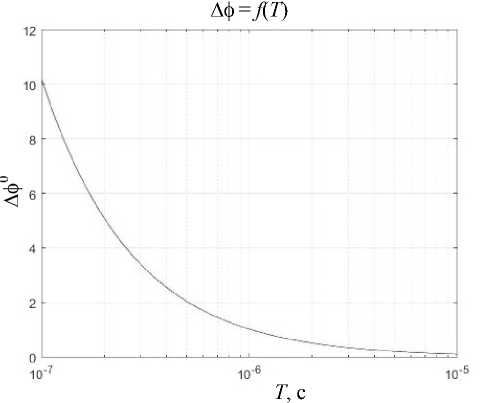
T , с

Рис. 9. График зависимости погрешности измерения разности фаз от периода сигнала при разновременном приеме сигналов

10"6

Δφ = f ( Δ t 1, 2 )

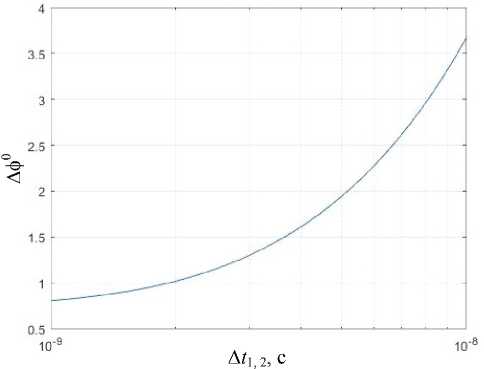
Рис. 11. График зависимости погрешности измерения разности фаз от погрешности измерения перехода сигнала через нулевой уровень при разновременном приеме сигналов

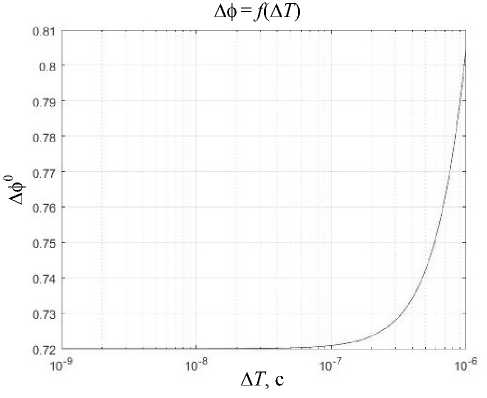
Рис. 10. График зависимости погрешности измерения разности фаз от погрешности измерения периода сигнала при разновременном приеме сигналов

ным компонентом, реализуется при измерении задержек, меньших 100 нс. При условии минимизации погрешностей, вносимых величинами измеряемой задержки и погрешностью измерения периода сигнала, суммарная погрешность будет приблизительно в раз больше, чем при классической реализации цифрового измерителя разности фаз, когда на входы измерителя подаются опорный сигнал и сигнал с измеряемой фазой. Однако если абсолютное откло нение частоты опорного генератора велико, то воз- можна ситуация, когда

тогда обе схемы

будут давать близкую по значению результирующую погрешность измерения разности фаз.

Продолжением работ является измерение разности фаз сигнала с присутствием шумов, усреднением по нескольким периодам с целью повышения точности, а также учетом траектории движения спутника.

Исследование выполнено при поддержке краевого государственного автономного учреждения « Красноярский краевой фонд поддержки научной и научно-технической деятельности » в рамках реализации проекта «Подготовка к внедрению программно-аппаратного комплекса для автоматизации испытаний бортовой аппаратуры командно-измерительной системы в АО " ИСС "» .