Измерение температуры термисторами

In the article we consider the problem of thermistor thermometry and increase of accuracy of such measurements. Such accuracy increase is achieved by means of temperature being attached to the inflection point T _inf of functional dependence of the logarithm of thermistor resistance, and the account of the timing drift of expansion coefficients.

Temperature measurement, thermistors, inflection point of the functional dependence of the logarithm of thermistor resistance, drift of expansion coefficients.

Проблема измерения температуры термисторами, применяемыми при исследовании тепловых процессов в устройствах охлаждения, например в тепловых трубах среднетемпературного диапазона, исключительно актуальна. При разработке новых тепловых труб сравнение и выбор тех или иных конструктивных вариантов проводится с помощью определения теплопередающих характеристик труб, и точность измерений температуры (разностей температур) при этом является решающим фактором.

С этой целью была выполнена калибровка термистора СТ3-19 в интервале температур 0÷200 ºC, путем сличения показаний в равновесных термодинамических условиях с образцовым платиновым термометром сопротивления [1; 2].

Экспериментальная часть. Термисторы СТ3-19 представляют собой термочувствительные элементы [3–5], выполненные из керамических оксидных материалов на основе никеля, марганца и кобальта, по составу определяемые формулой (Ni 0,2 Mn 0,7 Co 0,1 ) 3 O 4 , с отрицательным ТКС и сопротивлением при комнатной температуре около 10 кОм. Бусинка термистора СТ3-19 тонкими платиновыми проволочками (0,01 мм) приварена к выводным траверсам (0–3 мм) и покрыта тонким слоем молибденового стекла. Термисторы имеют радиационную стойкость не хуже 2 Ус и длительную выдержку при больших g .

В качестве термометра сопротивления использован чувствительный элемент образцового платинового термометра сопротивления ПТС-10. Кварцевый геликоид с платиновой спиралью помещен в выполненный из молибденового стекла тонкостенный цилиндрический чехол диаметром 4 мм. Перед запаиванием чехол с геликоидом был заполнен гелием при давлении, несколько меньшим атмосферного. После изготовления термометр сопротивления заново проградуирован в Сибирском институте метрологии (СНИИМ), г. Новосибирск, в интервале температур 0÷200 ºC. Абсолютная погрешность измерения температуры термометром оценена в 0,02 К.

Термометр с термистором размещены в массивном медном блоке цилиндрической формы, длиной 100 мм и диаметром 70 мм, установленном в вакуумной камере на специальных жестких подвесах, закрепленных на внутренней поверхности верхнего фланца камеры. В верхний фланец вакуумной камеры вварены две трубы, через одну из которых осуществляется вакуумная откачка камеры, а через другую выведены все измерительные провода. Вакуум в камере поддерживался не хуже 1,3·10–3 Па (10–5тор).

Вакуумная камера с медным блоком помещена в жидкостный термостат вместимостью 40 л, температуру в котором устанавливали и длительно поддерживали с помощью регулятора ВРТ-3 и платинового термометра ТСП-III в интервале 0 ^ 200 °С с минимальной дискретностью 5 -10-3 К. Охлаждающим устройством являлся кондиционер БК-1500, штатный испаритель-теплообменник которого был заменен разветвленным медным змеевиком. Рабочей жидко- стью в термостате служило силиконовое масло ПЭС-В2, позволяющее работать при температурах 0÷200 ºC. Колебания температуры внутри термостата на протяжении нескольких часов наблюдений не превышали 1·10–3 К, дрейф температуры был менее 1·10–4 К/час.

Проведение измерений. На протяжении нескольких лет в в ИТ СО РАН, Новосибирск, была осуществлена калибровка термисторов СТ3-19. Измерения проводились в стационарном режиме с изотермической оболочкой [6; 7], с постепенным увеличением температуры от 0 ºС до 200 ºС с шагом 10 ºС. Длительность одного непрерывного цикла подъема температуры и проведения измерений достигала 48 часов. Всего был проведен 21 цикл измерений.

Собственно калибровка термистора состояла в точном измерении стандартным потенциометрическим методом сопротивления термистора R C , Ом, в стационарном состоянии при заданной температуре Т , К, определяемой по платиновому термометру сопротивления ПТС-10. В качестве измерителя использован компаратор напряжений Р3003 класса точности 0,0005, вместе с образцовой катушкой сопротивления Р 321 класса точности 0,01, размещенной в пассивном термостате. Источником тока служил набор батарей «Бакен» в заземленном металлическом кожухе.

Всего получено более 500 экспериментальных точек, из которых был сформирован массив исходных данных температур T и логарифмов сопротивлений термистора ln R_C . Максимальная случайная погрешность измерения температуры термометром ПТС-10 не превышала (2÷3)·10^–3 К, сопротивлений термистора 5·10^–4 Ом.

Все измерения температуры, выполненные на термометре сопротивления ПТС-10, включая калибровку в СНИИМ, сделаны при величине измерительного тока 1 ma (1·10^–3 А), и выделяемая тепловая мощность равна W ПТС = (10÷17)·10^–6W.

На рис. 1 приведены результаты одного цикла измерений сопротивления термистора RC в зависимости от температуры, при этом для удобства дальнейшего анализа график представлен в виде функции обратной температуры 104/T, 1/К, от lnRC. Эта зависимость близка к линейной, но в области повышенных температур T ~ 473K, где lnRC ~ 4÷5, и в области пониженных температур T ~ 273K, где lnRC ~ 9÷10, наблюдаются отклонения. При средних температурах, в интервале значений lnRC ~ 6÷8, возможно существование точки перегиба.

Рассматривая датчик температуры как систему со сосредоточенными параметрами, уравнение термистора записывают следующим образом [1; 2]:

_т — WC Т ■ — CC Л л T C ^{+ т} C ■ T C =^7^ + T 0 ; ^т C , (1)

KCKC где TC – температура термистора, К; TC – производная по времени температуры термистора при динамическом режиме измерений, τC – характерное время запаздывания термистора, s; WC – выделяемая на термисторе электрическая мощность, W; KC – коэффициент теплопередачи между термистором и медным блоком, W/К; T0 – измеряемая термометром ПТС-10 температура медного блока или, например, тепловой трубы τ – время, s; CC – теплоемкость термистора, J /K.

Решением уравнения (1) является выражение (2) [8], в котором в момент времени τ = τ*

*

—

TC (т) = TC- expl1 +

к    ^т с )

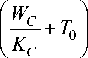
1 — exp

т —т

т с

температура термистора считается известной и равной T_C .

Электрическая мощность W C , выделяемая на термисторе измерительным током, при всех калибровочных испытаниях постоянна и равна 20·10^–6 W, и перегрев термистора Δ T C вычисляют по формуле

А Т_с

WW ----= т_г --. K C ^CC C

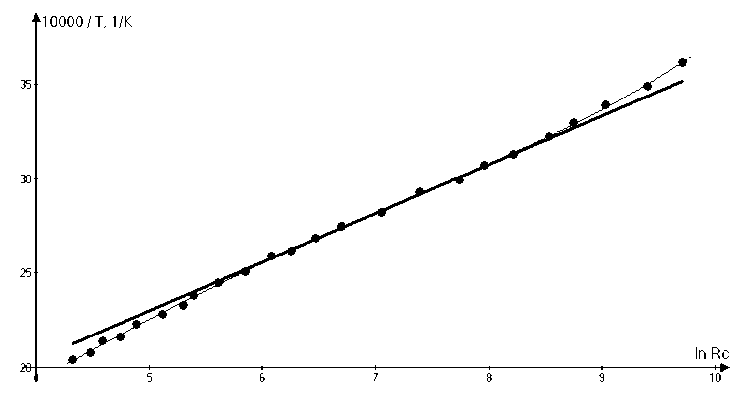
Рис. 1. Экспериментальная зависимость логарифма сопротивления термистора СТ3-19 от обратной температуры 10 ⁴ /T, 1/К. Прямая линия – расчет по уравнению (6); график кривой – расчет по уравнению (9)

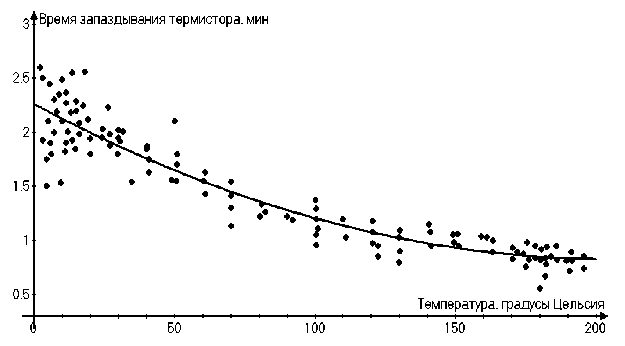
Рис. 2. Экспериментально определенные времена τ _C запаздывания термистора СТ3-19

Для определения перегрева термистора были проведены специальные опыты, в которых в стационарных состояниях при температурах от 2 до 195 ºC, измерялся темп нагрева и остывания термистора (и термометра) при ступенчатом изменении выделяемой в них электрической мощности W C . С помощью измерительной системы жидкостного калориметра, описание которой приведено в [6; 7], были проведены подробные измерения релаксационных характеристик датчиков. Расчет времени запаздывания термистора т С по уравнению (2) с помощью стандартной процедуры метода наименьших квадратов (МНК) [9–12] дал результаты, приведенные на рис. 2.

Аппроксимирующая кривая на рис. 2 задана полиномиальным выражением тС (t) = 3,3963027-10"5 ■ t2 -

• - 1,39779 ■ IO ^{- 2} ■ t + 2,261388 , мин,       (4)

где t – температура в градусах Цельсия, среднеквадратичное отклонение экспериментальных точек σ ~ 0,18 мин.

Теплоемкость термистора C C ~ (0,3÷0,35) Дж/К, коэффициент теплопередачи K C ~ (2÷5)·10^–3 W/K, величина перегрева измерительным током не превышает Δ T C ~ (10÷4)·10^–3 К и учитывается при всех измерениях.

Разность температур между медным блоком и окружающей ее изотермической оболочкой – термостатом – не превышала 0,05÷0,1 К, величина температурного хода при проведении калибровки была меньше 10–7 К/s, поэтому термодинамическое состояние датчиков температуры внутри медного блока в этот период являлось квазистационарным.

Обработка результатов. Функциональная зависимость электрического сопротивления оксидного полупроводникового термистора R_C от температуры Т достаточно сложна, и в первом приближении ее представляют в виде сопротивления идеального полупроводника со строго одинаковым количеством дырок и носителей заряда, в экспоненциальном виде

R c = A ■ exp I B\ ,                 ⁽⁵⁾

где R C – электрическое сопротивление термистора, Ом, при температуре T , К; A – величина сопротивления термистора, Ом, при бесконечно большой температуре; B – параметр чувствительности термистора, в общем случае также зависящий от температуры, 1/ К . При температуре t = 1 °C сопротивление термистора СТ3-19 R_C ~ 30 кОм, при температуре t = 200 ºC R_C ~ 50 Ом. Величина B ~ 4000 1/К, A ~ 0,013 Ом. После логарифмирования (5) получают

• 1    = - 1 ■ ln A + 1 ■ ln R .          (6)

TB BC

Для уточнения вопроса о перегибе, была вычислена производная d (1/ T )/ d (ln R C ), при этом анализировался весь массив экспериментальных точек. Значения производной d (1/ T )/ d (ln R C ), рассчитанные по результатам одного цикла измерений сопротивления термистора в зависимости от ln R C , приведены на рис. 3.

По результатам численного дифференцирования [13] всего массива экспериментальных точек, минимум кривой определен нами при значении lnRCmin = 7,63 ± 0,01, что соответствует температуре точки перегиба (inflection point) Tinf = 336,34 К или 63,19 ºC. Разлагая производную d(1/T)/d(lnRC) в ряд в окрестности точки минимума, было получено выражение d (1/T)            /               ,2

„ = a1 + a 2 ■( ln RC - 7,63) + dln RC

+ a ₃ ■ ( ln R C - 7,63 ) 3 + ...             (7)

где a i – коэффициенты разложения.

После интегрирования разложение (7) приводят к следующему виду

T = Ao (тd) + A1 (тd)■(lnRc -7,63) + A2 (тd)x x (InRc - 7,63)3 + A3 (тd) ■ (InRc - 7,63)4,    (8)

где A_i (τ _d ) – коэффициенты разложения; τ _d – время дрейфа (drift) коэффициентов.

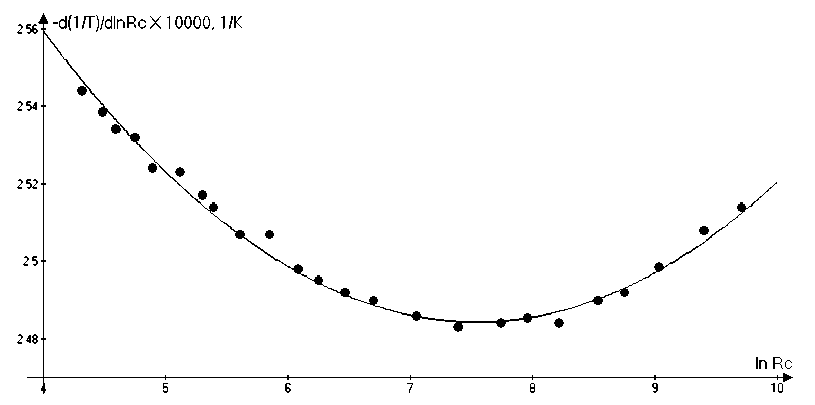
Рис. 3. Расчетная зависимость производной – d (1/ T )/ d (ln R C )·10 ⁴ ,1/ K , в зависимости от логарифма сопротивления ln R_C термистора СТ3-19

Таким образом, калибровка термистора СТ3-19 по существу, состоит в определении численного значения коэффициентов полинома (8) A i (τ d ) и учета их дрейфа во времени.

Основная особенность расчета по уравнению (8) заключается в привязке температуры к точке перегиба T _inf функциональной зависимости логарифма сопротивления термистора.

Расчет коэффициентов A i (τ d ) был проведен с помощью стандартной процедуры метода наименьших квадратов (МНК) [9–12]. Абсолютные погрешности расчета коэффициентов A_i (τ _d ) следующие: δ A ₀ ~1·10^–3, δ A 1 ~1·10^–3, δ A 2 ~1·10^–4, δ A 3 ~1·10^–5.

Для контроля качества калибровок и их долговременной стабильности после каждого из 21 определения набора коэффициентов A i (τ d ) из выражения (8) были вычислены производные d (1/ T )/ d (ln R C ). С разбросом не более ∑~ 5·10^-7 все значения производных лежат на кривой рис. 3. В области пониженных температур при значениях логарифмов ln R C ~ 9÷10, разброс калибровок несколько больше и достигает ∑ ~ (5÷7)·10^-7. Связано это с тем, что там, где больше сопротивление термистора R_C и круче его температурная зависимость dR_C / dT , там меньшая плотность экспериментальных точек, поскольку калибровки термистора преимущественно проводились равномерно по температуре с шагом 10 ºC.

Динамика изменения коэффициентов A i (τ d ), временной дрейф калибровки термистора представлена на рис. 4. Первые восемь циклов измерений проводились с нагревом термистора до температуры 200 ºС. Следствием такого нагрева был значительный дрейф калибровки и изменение коэффициентов A i (τ d ), например dA 0 / d τ ~ 6·10^–4 1/мес.

После того как верхний предел температуры был снижен до 190 ºC, временной дрейф коэффициентов заметно уменьшился, к примеру скорость изменения коэффициента A 0 (τ d ) стала всего dA 0 / d τ ~ 1,5·10^–4 1/мес. Значения временного дрейфа коэффициентов A i (τ d ) приведены ниже, τ d – месяцы.

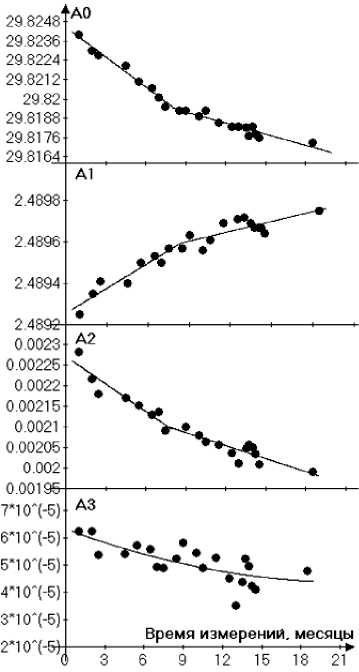
Рис. 4. Динамика изменений коэффициентов A_i во времени при нагревах до 200 ºC – левые части графиков, до 190 ºC – правые части графиков

Коэффициент A 0 (τ d ):

A 0 = – 6,21997·10^–4·τ d + 29,824488 при нагреве до 200 ºС;

A 0 = – 2,3075444·10^–4·τ d + 29,819432 при нагреве до 190 ºС.

Коэффициент A₁(τ _d ):

A₁ = 4,051207·10^–5·τ _d + 2,489278 при нагреве до 200 ºС;

A₁ = 1,5876991·10^–5·τ _d + 2,48958 при нагреве до 190 ºС.

Коэффициент A₂(τ _d ):

A 2 = – 2,2266277·10^–5·τ d + 0,0022733 при нагреве до 200 ºС;

A 2 = – 1,0559017·10^–5·τ d + 0,0021054 при нагреве до 190 ºС.

Коэффициент A 3 (τ d ):

A 3 = – 3,98635·10^–8 ·(τ d )² + 1,771915·10^–6 ·τ d + 6.3241 ·10^–5 при нагреве до 190 ºС и до 200 ºС.

Подстановка коэффициентов A_i (τ _d ), вычисленных при нагреве термистора до 190 ºC в уравнение (8), снижает разброс производных d (1/ T )/ d (ln R_C ) на кривой рис. 3 до величины ∑ ~ (2÷3)·10^–7, и позволяет более точно определить точку минимума In R C min = 7,63 2 ± 0,01, тем самым уменьшить погрешность расчета температуры при проведении измерений термистором СТ3-19.

Таким образом, рекомендуемое уравнение для расчета температуры термистором СТ3-19, учитывающее как точку перегиба (inflection point)

T inf = 336,34 К функциональной зависимости логарифма lnR C сопротивления термистора, так и временной дрейф полиномиальных коэффициентов разложения A_i (τ _d ) при периодических нагревах термистора до 190 ºC, выглядит следующим образом:

T = A 0 (^Т d )⁺ A 1 (^Т d Мln R C ^{- 7,63} 2 ) ⁺

A 2 ( т d ) • ( ln R C - 7,63 2 ) ³ + A 3 ( т d ) • ( ln R C - 7,63 2 )⁴ • (9)

О бсуждение результатов. Известно полиномиальное уравнение третьей степени J. S. Steinhart, S. R. Hart [14], предназначенное для расчета температуры термистором и содержащее линейный и кубический по логарифму сопротивления ln R C члены

---= A + B • In R _c + C • In R ³_c.      (10) T SH

Диапазон применения по температуре данного уравнения с одним набором коэффициентов не превышает 50 ÷75 К [14; 15]. Используя опубликованные в современных интернет-изданиях [15] наборы численных значений коэффициентов уравнения Steinhart`a и Hart`a, было проведено сопоставление результатов расчета температуры по уравнению Steinhart`a и Hart`a и по нашему уравнению четвертой степени логарифмов сопротивления термистора (9).

Относительные разности температур

δ = (TSH – T) /T·100 %, в зависимости от lnRC представлены на рис. 5. Проведенное сопоставление результатов показывает, что разности температур δ в зависимости от lnRC имеют знакопеременный характер.

Минимальные значения разностей температур δ порядка 0,25 %, наблюдаются при величине ln R C ~ 6 термистора СТ3-19. Максимальные значения разностей δ, достигающие 0,8 ÷1 %, имеют место на краях интервала применимости уравнения (9).

Погрешность определения температуры (разностей температур) термистором СТ3-19 с помощью уравнения четвертой степени (9) с учетом точки перегиба при ln R C = 7,63 2 , не превышает (3÷5)·10^–4 К.

Применение полиномиального уравнения четвертой степени (9) с привязкой температуры к точке перегиба функциональной зависимости логарифма сопротивления термистора, позволяет расширить диапазон и повысить точность определения температуры.

Учет временного дрейфа коэффициентов разложения полинома (9) A i (τ d ) позволяет повысить точность определения точки минимума In R C min = 7,63 2 ± 0,01 характеристик термистора и тем самым точность определения температуры.

Применение полиномиального уравнения третьей степени Steinhart`a и Hart`a увеличивает погрешности расчета температуры термистором на краях интервала 273 К ÷ 473 К до 1,5÷2 К.

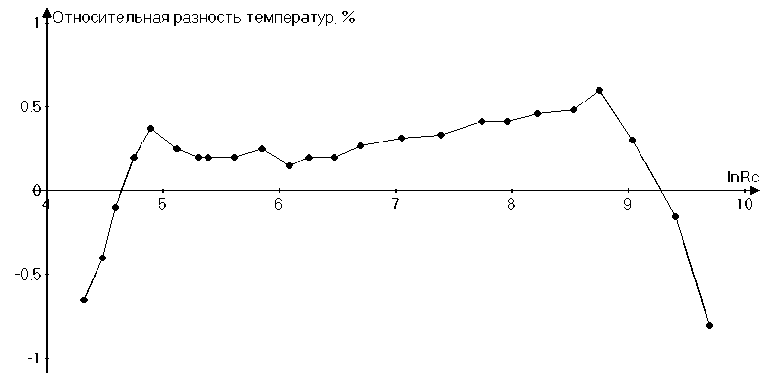
Рис. 5. Относительные разности температур δ, вычисленные по уравнению Steinhart`a и Hart`a, и по уравнению четвертой степени относительно точки перегиба характеристик термистора (9)